基于經驗模態分解方法和信息熵的水沙關系研究

張金萍，肖宏林，張 鑫

(鄭州大學水利與環境學院，河南 鄭州 450001)

黃河以泥沙多而聞名，因泥沙淤積造成的黃河水患給國家和人民造成了極大危害。因此，研究黃河徑流-泥沙關系及其演化特征具有重要的意義。胥維坤[1]運用統計學方法分析了小浪底水庫運行后對黃河下游水沙變化的影響。方怒放[2]把三峽水利樞紐中的王家橋小流域作為研究區，利用多元相關分析和逐步回歸分析研究了降雨、徑流、泥沙三者之間對應的關系性。吳敬東等[3]建立了小流域坡面不同治理措施下的徑流量與降雨量、降雨歷時之間的數學模型,確定了徑流量和輸沙量之間的關系。河川水沙常常受多種水文因素的影響，在不同時間尺度下呈現復雜的波動特征和關系特性，因此對水沙研究應包含時序多時間尺度細部演化特征分析[4]。本文針對流域產匯流系統在多時間尺度下的徑流-泥沙關系，通過經驗模態分解(empirical mode decomposition, EMD)方法分析其原始序列的細部演變規律和特征，同時結合信息熵理論，辨識河流水沙關系及其演化特征。

1 數據來源及研究方法

1.1 數據來源

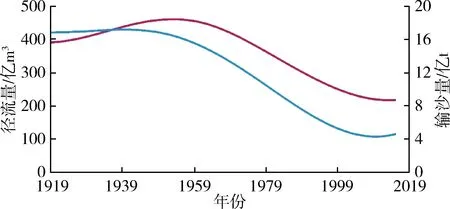
潼關水文站位于黃河中游，是黃河上第二大水文站，潼關斷面在黃河、北洛河、渭河3條河流匯流下游不遠處，洪水常常在這里相遇，洪水此消彼長，水沙條件復雜。本研究獲取了潼關水文站1919—2015年實測徑流量和輸沙量資料作為研究數據。潼關水文站地理位置和研究時段內的年徑流量、輸沙量原始序列分別見圖1、圖2。

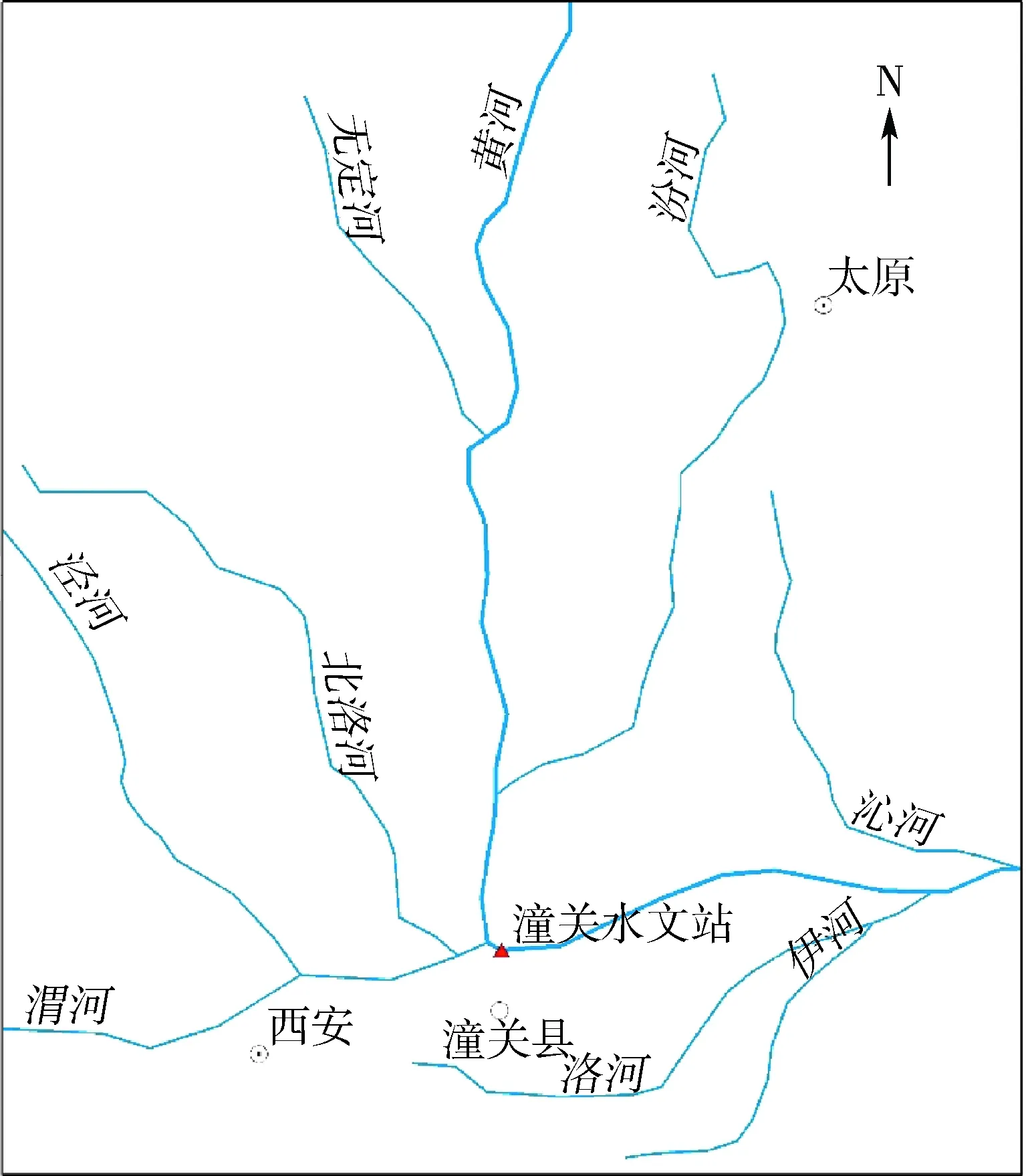
圖1 潼關水文站地理位置

圖2 徑流、泥沙原始序列

1.2 研究方法

1.2.1EMD方法

EMD方法是Huang等[5]于1998年提出的一種新型自適應信號時頻分析方法，近年來在水文水資源領域廣泛應用[6]。該方法是通過一個“篩選”過程從被分析原始信號中分離本征模函數(intrinsic mode function, IMF)，并且提取的IMF分量需要滿足以下條件：①在整個時段內包含所有數據信息的集合中，其數據極大值點與極小值點的數量必須等于經過0點的數量或者數量差值為一個；②在任何時刻，其數據的極大值點連接形成的包絡線與極小值點連接形成的包絡線的總體均值最終為0[7]。對于復雜信號若不滿足IMF所要求的條件，可以利用EMD方法按照分解的步驟對復雜信號進行分解形成一系列滿足條件的IMF分量[8]。EMD方法的步驟為：

步驟1：首先定義一個原始信號為X(t)。

步驟2：分析原始信號X(t)找出它全部的極大值點與極小值點及其對應位置，并利用插值方法處理形成上下包絡線，求出極大值點和極小值點形成的包絡線的均值M1和原始信號X(t)與均值M1之間的差值H1，即H1=X(t)-M1。若H1滿足IMF的兩個條件，則進行步驟4，否則進行步驟3。

步驟3：把H1看作原始信號重復步驟2求得上下包絡線形成的均值M2，再通過上述方法計算出差值H2，并判斷其是否滿足IMF的條件，若還不滿足繼續重復直至找到滿足IMF條件的分量。

步驟4：將第一個IMF分量從X(t)中分離，從而得到R1，即R1=X(t)-H1。

步驟5：重新把分離后的差值R1看作原始信號并重復步驟2～4得到n個滿足條件的IMF分量和1個趨勢項(residual, RES)分量Rn，從而完成對原始信號的分解過程。

通過以上步驟可將潼關水文站徑流量、輸沙量進行EMD分解，提取多個IMF分量。

1.2.2信息熵理論

Shannon[9]參考熱力學上的知識，把信息熵定義為排除了信息冗余后的平均信息量。若系統變量有U1，U2，…，Un共n種取值，對應概率分別為：P1，P2，…，Pn且各種取值的出現彼此獨立，此時信源的平均不確定性應為每個符號不確定性-lnPi統計得到的數學期望稱為信息熵[10-11]。信息熵H(U)的計算公式為

(1)

信息論中用信息熵來表示系統本身所擁有信息量的多少。一個系統表現得越穩定、越有規律，則該系統對應的信息熵值就越小，所以信息熵也用來表示系統的穩定性程度、有序化程度[12-13]。

互信息在信息論中表示兩變量之間的相關性，它反映隨機變量之間共有的信息量或相互間的依賴關系[14]。若兩隨機變量間的聯系越緊密，則它們的互信息熵值就越大，同理在相反情況下，則兩者之間的互信息熵值就越小[15]。

分別計算徑流、泥沙原序列及分解后的IMF分量的信息熵，并通過計算徑流、泥沙的互信息從而確定黃河流域徑流-泥沙的關系。以潼關水文站實測徑流量或輸沙量為例，設原始信號X(t)為潼關水文站1919—2015年徑流量或輸沙量數據，經EMD分解可得到n個不同的IMF分量，每個分量包含m年的實測分解值。則得有判定矩陣：

C=(Cst)n×m(s=1,2,…,n；t=1,2,…,m)

(2)

式中Cst為第s個IMF分量的第t年的實測分解值。

為了排除干擾，在計算各IMF分量的信息熵時，首先需要對n個IMF分量的所有數據作歸一化處理。得到歸一化矩陣B,歸一化處理公式為

(3)

式中：Bst為B的元素；Cmax、Cmin分別為同一IMF分量系列數據的最大值和最小值。

將區間[0,1]平均分成L組，每組長度為1/L，對應的區間為[0，1/L)，[1/L，2/L)，…，[L-1/L，1]。對于某個IMF分量m年歸一化數據中第t年在相應的某個分組區間內的概率Pl為t/m[16]。由信息熵的定義和計算公式知，為保證lnPl始終有意義，需要對Pl進行修正，即當Pl為0時假設lnPl為0。則第s個IMF分量的信息熵為

(4)

根據式(4)可依次求出經EMD分解的IMF分量信息熵值，同理求得趨勢項的信息熵值。在此基礎上，利用式(5)求出它們之間的互信息熵，得出相互間的關聯度。

MI(a,b)=H(a)+H(b)-H(a,b)

(5)

式中：MI(a,b)為互信息熵值；H(a)、H(b)分別為徑流量、輸沙量各分量的信息熵；H(a,b)為二者對應各分量之間的聯合熵。

2 結果分析

2.1 EMD方法分析

應用前文EMD分解步驟對潼關水文站1919—2015年徑流量、輸沙量原始序列進行分解，分別得到徑流量和輸沙量的4個IMF分量與1個RES分量。徑流量、輸沙量各分量序列見圖3。

由圖3可知，徑流量和輸沙量均包含著復雜得多時間尺度周期性變化和宏觀趨勢走向。徑流量和輸沙量IMF1分量對應的準周期約為5 a和4 a，IMF2分量的準周期約為8 a和6 a，IMF3分量的準周期約

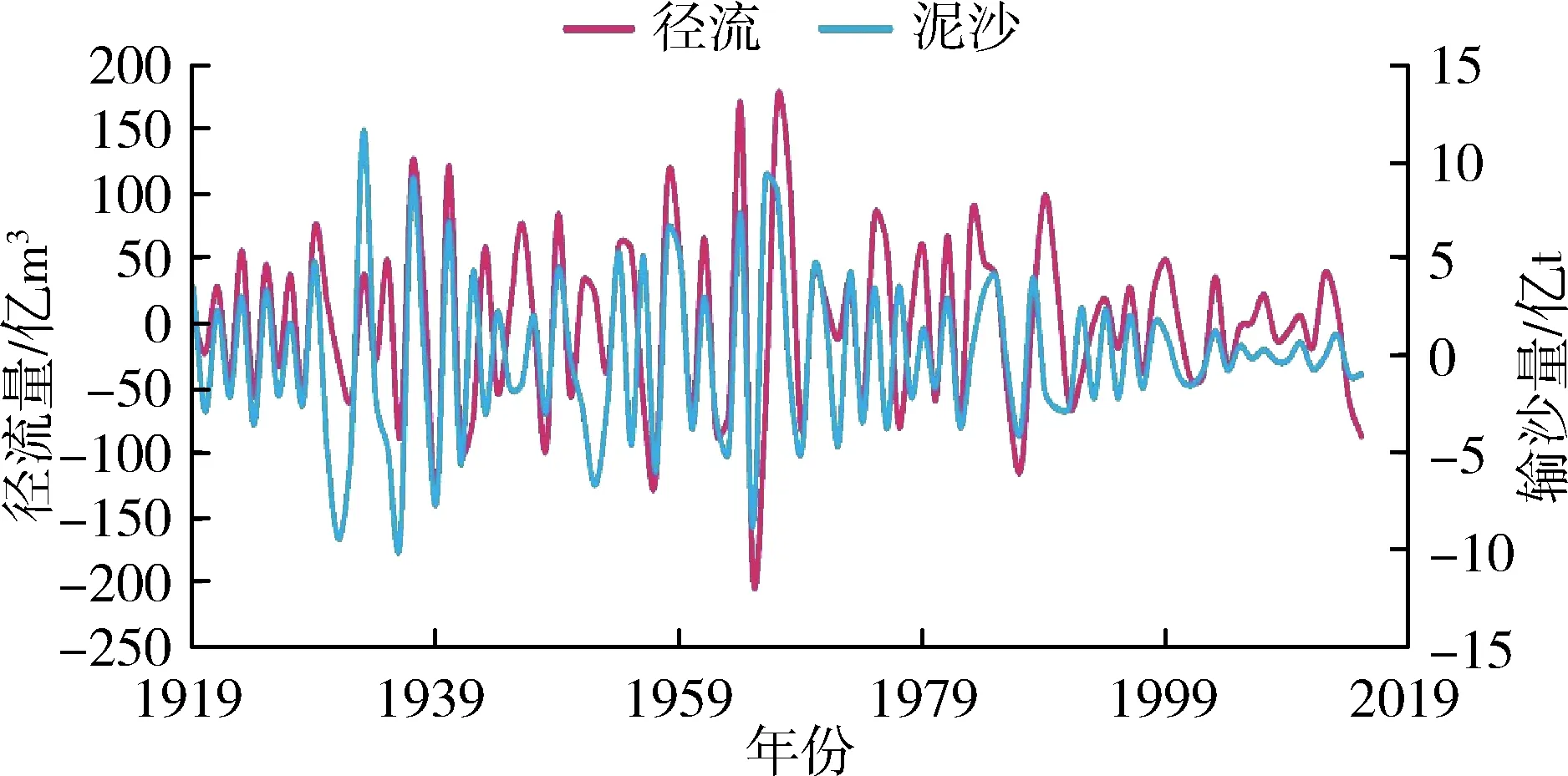
(a)IMF1分量

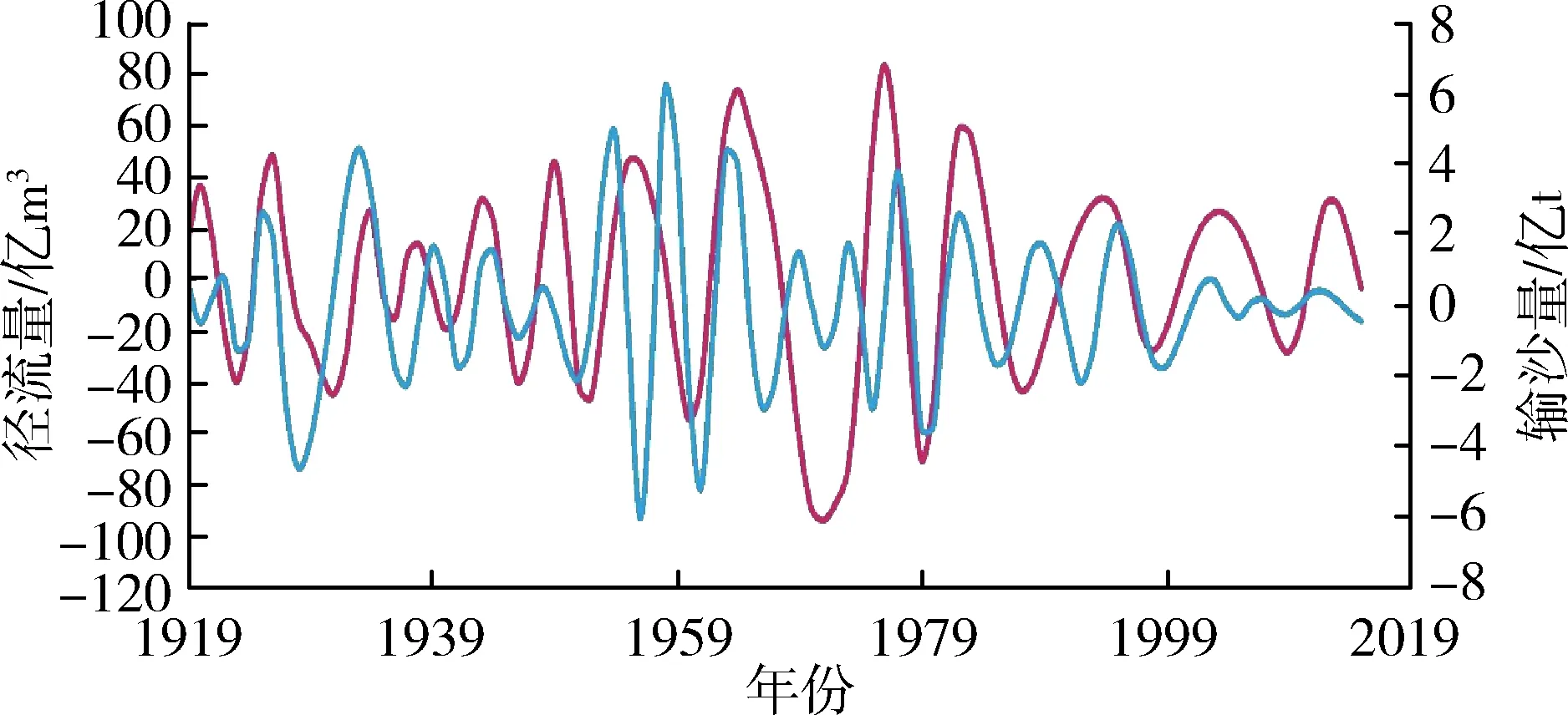
(b)IMF2分量

(c)IMF3分量

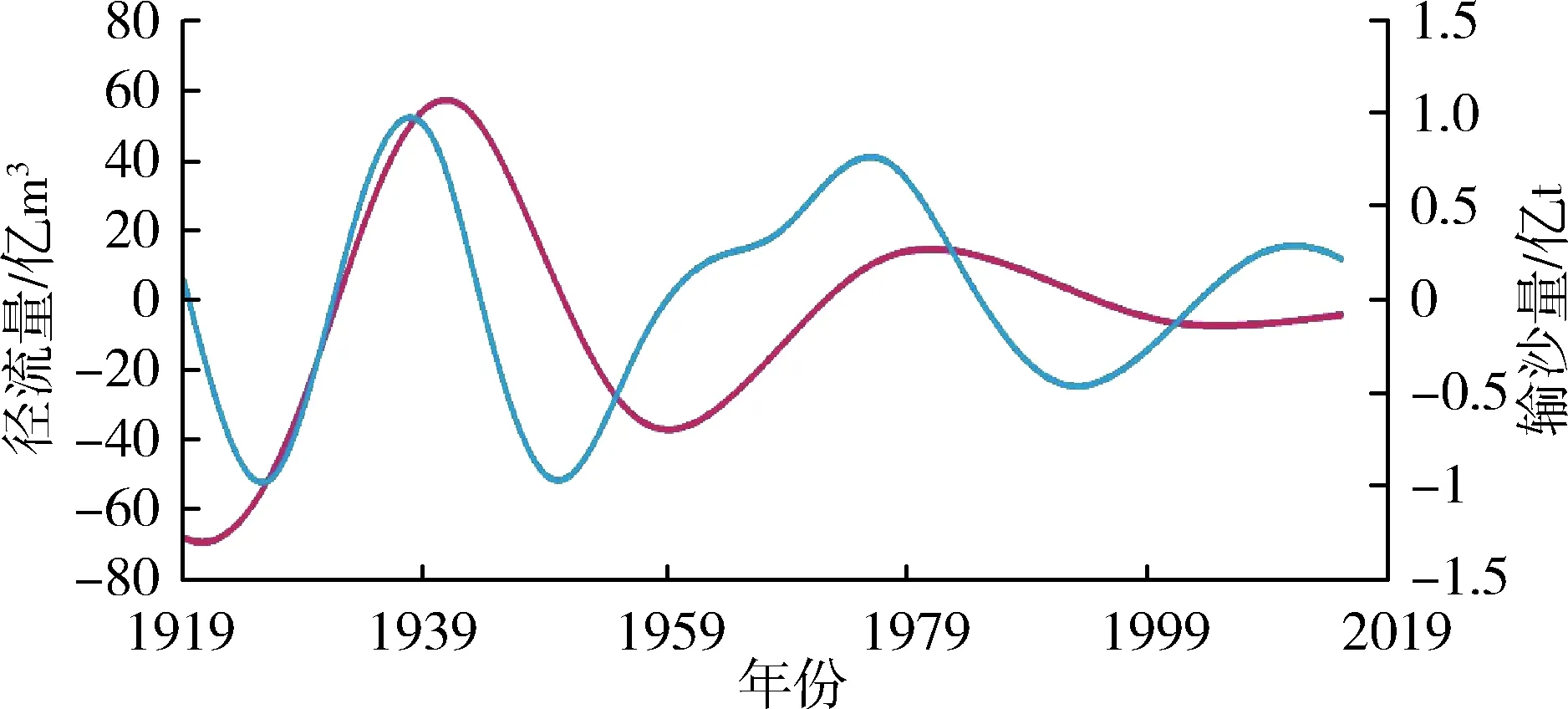
(d)IMF4分量

(e)RES分量

為16 a和15 a，IMF4分量的準周期約為35 a和28 a，可見徑流和泥沙各IMF分量周期性關系在不同時間尺度上變化規律基本保持一致。這表明水沙相關性密切，水沙長時間序列在模糊特征下具有確定性特征，即存在波動周期的確定性，可為不同時期水沙聯合預測、水沙變化特征研究提供參考。徑流量、輸沙量原始序列影響因素較多，經過EMD分解后隨著分解層數的增多分解尺度的加大，徑流、泥沙的干擾信息被去除，影響因素減少，有效信息增多，在不同的分層下表現為越來越有規律性。在趨勢變化方面，表現為分解序列更有序，系統由無序到有序過渡的趨勢性。特別是徑流量、輸沙量的趨勢項呈現出較強的規律性，都呈現先上升后逐漸下降的趨勢，徑流上升速度比泥沙上升速度略快，二者趨勢走向基本同步。

潼關水文站徑流量、輸沙量的趨勢項在1950年左右分別出現拐點，在之后很長一段時間內不斷減少，這是受自然和人類活動等多重因素影響的結果。1949年以來，水利工程建設、河道外取水、水土流失綜合治理措施和修建淤地壩等生態工程建設的增加及其他人類活動干預對水文系統產生重大影響，使潼關水文站徑流量，輸沙量出現明顯的減少[17]。整體而言，年徑流量與年輸沙量隨時間表現為顯著下降的趨勢與文獻[18]的結論相符。這表明原序列經EMD分解的RES分量可以反映徑流量、輸沙量整體的變化趨勢，即低頻模態分量控制著序列變化的全局和趨勢。

2.2 信息熵分析

利用前文方法計算徑流量、輸沙量分解序列的信息熵結果見表1。徑流量、輸沙量IMF1分量對應的波動周期為短周期，IMF2分量對應的波動周期為中周期，IMF3分量對應的波動周期為中長周期，IMF4分量對應的波動周期為長周期，因RES分量缺乏周期波動，故不與IMF分量作對比。

表1 徑流量與輸沙量分量信息熵

由表1可見，徑流量和輸沙量原序列熵值較大，徑流量熵值拐點首次出現在IMF1處，輸沙量熵值拐點出現在IMF2處。表示隨著分解層數的增多、分解尺度的加大，徑流、泥沙分解序列表現為越來越有序，影響因素越來越少，系統呈現由不穩定向穩定過渡、由無序到有序的過渡的趨勢性，因此信息熵值減小。但當分層過多，分解尺度過大，使系統的其他影響因素體現出來，從而使得信息熵值增大。

原序列對應的徑流熵值比泥沙熵值稍大，可以判定徑流系統較泥沙復雜，須密切關注徑流量的變化。徑流、泥沙各序列信息熵值變化基本同步，則表明徑流量、輸沙量之間關系應表現為同步變化或者異步變化特征，由徑流量、輸沙量原序列經EMD方法分析得知二者滿足同步變化關系。

2.3 互信息分析

為了深層次分析潼關水文站徑流-泥沙的關系，計算各序列與原序列之間的互信息熵值以及徑流量與輸沙量原序列之間的互信息熵值，結果見表2。

表2 徑流量和輸沙量原序列與其分解序列之間的互信息熵值

由表2可知，徑流量、輸沙量的原序列與RES分量之間的互信息最大，可見如果徑流、泥沙系統比較復雜，為了便于研究徑流、泥沙變化可采用RES分量數據信息闡述原始數據信息，并利用趨勢項變化特征觀察其整體發展態勢。徑流原序列與各IMF分量的互信息呈現遞增的趨勢性，即它們之間的共有信息量越來越多，原序列與IMF4的互信息最大，說明IMF4對徑流原序列的貢獻程度最大。對于徑流IMF分量而言，低頻分量與原序列的互信息較大，所以低頻分量所攜帶的信息量比較多，因此對徑流量宜采用長周期研究比較可靠。泥沙原序列與各IMF分量的互信息先減小后增大,泥沙原序列與IMF1互信息最大，說明IMF1對泥沙原序列的貢獻率最大。對于泥沙IMF分量而言，高頻分量與原序列的互信息較大，高頻分量所攜帶的信息量比較多，因此對輸沙量宜采用短周期研究比較可靠。

為了更進一步研究徑流量、輸沙量之間的關系，計算了徑流與泥沙之間原序列及各分解序列的互信息熵值，原序列之間為0.689，IMF1分量之間為0.575，IMF2分量之間為0.338，IMF3分量之間為0.534，IMF4分量之間為0.675，RES分量之間為1.410。可以看出，趨勢項之間的互信息最大，這是由于經EMD方法分解后排除了干擾，使徑流、泥沙的有效信息充分體現出來，從而使兩者之間的趨勢項互信息比原序列之間的互信息大。原序列之間互信息也較大，表示雖然徑流、泥沙原序列的影響因素比分解序列要復雜，系統比較無序，但是原序列信息量比較多。對于各分解序列來說，互信息基本呈現遞增的趨勢性，表示經EMD分解排除干擾后各系列之間的關聯性增大，它們之間的共有信息量逐漸增大。對于徑流量與輸沙量經EMD分解的各IMF分量而言，徑流量與輸沙量對應的長周期IMF4分量互信息最大，因此徑流量與輸沙量關系及其變化特征宜采用長周期的研究。

3 結 論

潼關水文站年徑流量與年輸沙量隨時間表現為顯著下降的趨勢，且徑流量和輸沙量有著很強的相關性，這種相關性不僅體現在宏觀趨勢上，而且還體現在微觀局部特征上，具體表現為在多時間尺度下波動特征基本同步。EMD方法與信息熵結合分析表明，徑流量與其長周期分量互信息最大，因此對徑流量變化特征宜采用長周期研究比較可靠；輸沙量與其短周期分量互信息最大，因此對輸沙量變化特征宜采用短周期研究比較可靠；而徑流量與輸沙量的長周期分量及趨勢項互信息較大，所以黃河中游潼關附近水沙關系可采用長周期研究，趨勢項分量數據信息闡述原始數據信息比較可靠。