基于HPSO-BP神經(jīng)網(wǎng)絡(luò)融合的鋰電池SOC預(yù)估研究*
于仲安 褚彪 葛庭宇
(江西理工大學(xué),贛州 341000)
主題詞:荷電狀態(tài) 磷酸鐵鋰電池 混合粒子群算法 BP神經(jīng)網(wǎng)絡(luò)
1 前言
動(dòng)力電池荷電狀態(tài)(State Of Charge,SOC)的預(yù)測(cè)在電池管理系統(tǒng)(Battery Management System,BMS)中具有極其重要的地位,準(zhǔn)確預(yù)測(cè)電池SOC不僅能夠提高電池系統(tǒng)的安全性,避免電池過(guò)充、過(guò)放,延長(zhǎng)使用壽命,而且可以優(yōu)化駕駛和提高電動(dòng)汽車的使用性能[1]。目前主流的鋰電池SOC估計(jì)方法有安時(shí)積分法、開(kāi)路電壓法、內(nèi)阻法、卡爾曼濾波法、人工神經(jīng)網(wǎng)絡(luò)法等。這些方法都有各自的優(yōu)缺點(diǎn),通過(guò)一定的改進(jìn)與聯(lián)合,可以提高鋰電池SOC的預(yù)測(cè)精度。文獻(xiàn)[2]提出由標(biāo)準(zhǔn)卡爾曼濾波器和無(wú)味卡爾曼濾波器組成的雙重過(guò)濾器,用以預(yù)測(cè)電池內(nèi)部狀態(tài);文獻(xiàn)[3]利用非線性預(yù)測(cè)濾波器(Nonlinear Predictive Filter,NPF)電荷估計(jì)方法,可以任意統(tǒng)計(jì)分布形態(tài),準(zhǔn)確估計(jì)電池的SOC;文獻(xiàn)[4]提出一種基于改進(jìn)滑模觀測(cè)器的SOC估計(jì)算法,采用sigmoid函數(shù)代替?zhèn)鹘y(tǒng)滑模觀測(cè)器中的符號(hào)函數(shù),并對(duì)觀測(cè)器中的模型參數(shù)進(jìn)行在線更新,進(jìn)一步消除參數(shù)變化帶來(lái)的模型誤差,從而提高估計(jì)精度;文獻(xiàn)[5]提出基于遞歸非線性自回歸(Nonlinear Autoregression with Exogenous,NARX)神經(jīng)網(wǎng)絡(luò)模型,利用閃電搜索算法(Lightning Search Algorithm,LSA)尋找輸入延遲、反饋延遲和隱藏層神經(jīng)元的最佳值,對(duì)鋰離子電池進(jìn)行了精確而可靠的SOC估計(jì);劉艷麗等[6]提出有限差分?jǐn)U展卡爾曼濾波算法,用于鋰電池SOC的估算,取得了很好的精度;李哲等[7]通過(guò)修正初始SOC值,提高安時(shí)積分法的精度,對(duì)后續(xù)的SOC估算精度提高有很大的參考價(jià)值。
人工神經(jīng)網(wǎng)絡(luò)擁有強(qiáng)大的自學(xué)習(xí)能力,能夠通過(guò)對(duì)訓(xùn)練樣本數(shù)據(jù)的學(xué)習(xí)實(shí)現(xiàn)對(duì)輸入、輸出間內(nèi)在規(guī)律的刻畫(huà),因此具有高度的非線性能力,此外,還擁有優(yōu)秀的容錯(cuò)性和魯棒性,非常適合應(yīng)用于鋰電池SOC的估算[8]。BP算法理論依據(jù)堅(jiān)實(shí)、通用性好,至今仍是前向網(wǎng)絡(luò)學(xué)習(xí)的主流算法,但其同時(shí)存在著本質(zhì)缺點(diǎn):容易陷入局部極小,收斂速度較慢,學(xué)習(xí)率不易選擇。
遺傳算法(Genetic Algorithm,GA)遵循“優(yōu)勝劣汰,適者生存”原則,具有全局最優(yōu)的特點(diǎn)。將遺傳算法與BP網(wǎng)絡(luò)結(jié)合起來(lái)形成GA-BP網(wǎng)絡(luò)算法,可以克服BP算法陷入局部最優(yōu)的缺點(diǎn),提高網(wǎng)絡(luò)穩(wěn)定性。標(biāo)準(zhǔn)粒子群算法在基本粒子群算法的基礎(chǔ)上引入了慣性權(quán)重w,適當(dāng)選擇w的大小可以使得算法具有廣域搜索能力和局部搜索能力,然而依然避免不了陷入局部最小的問(wèn)題[9-10]。
粒子群算法比較簡(jiǎn)便、易于實(shí)現(xiàn),沒(méi)有過(guò)多參數(shù)需要調(diào)整,本文采用HPSO-BP算法,將粒子群算法與遺傳算法中的交叉變異思想結(jié)合起來(lái),用于優(yōu)化BP神經(jīng)網(wǎng)絡(luò)中的初始權(quán)值和閾值,可以提高收斂速度,克服易陷入局部極小的缺點(diǎn)。
2 基于BP神經(jīng)網(wǎng)絡(luò)的鋰電池SOC預(yù)測(cè)模型
根據(jù)Kolmogorov定理,3層的前向網(wǎng)絡(luò)在隱層神經(jīng)元數(shù)目足夠多的情況下,能夠以任意精度對(duì)非線性函數(shù)進(jìn)行映射。本文采用應(yīng)用最為廣泛的BP神經(jīng)網(wǎng)絡(luò)對(duì)鋰離子電池SOC進(jìn)行預(yù)測(cè)。將鋰電池的工作電壓U、工作電流I、內(nèi)阻R、環(huán)境溫度T作為電池SOC的影響因子,即SOC=f(V,I,R,T)。圖1所示為BP神經(jīng)網(wǎng)絡(luò)SOC預(yù)測(cè)模型。
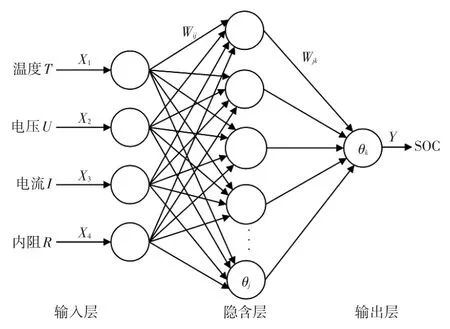
圖1 基于BP神經(jīng)網(wǎng)絡(luò)的SOC預(yù)測(cè)模型
BP網(wǎng)絡(luò)的輸入矢量為[X1,X2,X3,X4],網(wǎng)絡(luò)輸入層節(jié)點(diǎn)數(shù)n=4,電池SOC作為輸出矢量[Y],輸出節(jié)點(diǎn)數(shù)為l=1,根據(jù)經(jīng)驗(yàn)公式m=(n+l)0.5+a(a為[1,10]范圍內(nèi)的常數(shù)[11]),經(jīng)過(guò)多次仿真試驗(yàn),設(shè)m=12時(shí),網(wǎng)絡(luò)的誤差精度更高,收斂速度也更快。網(wǎng)絡(luò)激活函數(shù)選用tansig函數(shù),性能函數(shù)選為均方誤差性能函數(shù)(Mean Squared Error,MSE)。
3 混合粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)
3.1 標(biāo)準(zhǔn)粒子群算法
粒子群優(yōu)化(Particle Swarm Optimization,PSO)算法是由Eberhart博士和Kennedy博士于1995年提出的一類群智能隨機(jī)優(yōu)化算法,其思想源于對(duì)鳥(niǎo)群捕食行為的研究[12]。在粒子群算法中,每個(gè)粒子都代表著問(wèn)題的一個(gè)潛在最優(yōu)解,對(duì)應(yīng)著適應(yīng)度函數(shù)決定的適應(yīng)度值,其大小決定著解的優(yōu)劣程度。在每一次迭代中,粒子通過(guò)跟蹤個(gè)體極值pbest和全局極值gbest更新自身的速度和位置。
粒子i的信息用D維向量表示,包括速度信息vi=(vi1,vi2,…,viD)T和位置信息xi=(xi1,xi2,…,xiD)T,速度和位置的更新公式分別為:
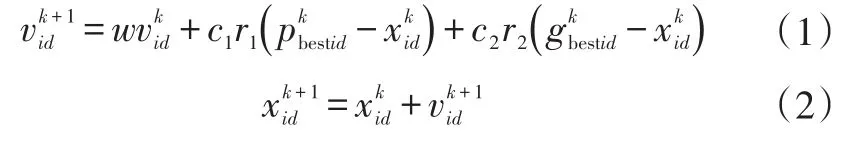
式中,d∈[1,D]為維數(shù);w為慣性權(quán)重;k為當(dāng)前迭代次數(shù);c1、c2為學(xué)習(xí)因子或者加速系數(shù),通常取為2;r1、r2為[1,0]區(qū)間內(nèi)均勻分布的偽隨機(jī)數(shù)。
慣性權(quán)重的大小決定了粒子對(duì)當(dāng)前速度繼承的多少,合理選擇可使粒子具有均衡的探索能力(廣域搜索能力)和開(kāi)發(fā)能力(局部搜索能力),目前調(diào)整慣性權(quán)重w的策略有線性調(diào)整、模糊調(diào)整、隨機(jī)調(diào)整等。模糊調(diào)整策略參數(shù)比較多,增加了算法的復(fù)雜度;隨機(jī)調(diào)整策略在面臨動(dòng)態(tài)優(yōu)化問(wèn)題時(shí),不能預(yù)測(cè)粒子群需要更好的探索能力還是開(kāi)發(fā)能力;線性調(diào)整策略使算法前期具有全局搜索能力,后期具有局部搜索能力,并且調(diào)整策略簡(jiǎn)單易行,符合實(shí)際優(yōu)化問(wèn)題的一般策略。故本文采用線性調(diào)整策略:
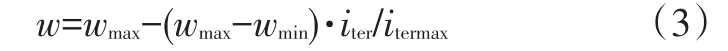
式中,wmax、wmin分別為慣性權(quán)重的最大值和最小值;itermax、iter分別為最大迭代次數(shù)和當(dāng)前迭代次數(shù)。
一般將慣性權(quán)重初始化為0.9,隨著迭代次數(shù)的增加,w線性遞減至0.4。
3.2 混合粒子群算法
粒子群算法雖然具有收斂速度快、操作簡(jiǎn)單等優(yōu)點(diǎn),但是隨著迭代次數(shù)的增加,種群達(dá)到收斂時(shí),個(gè)體粒子越來(lái)越相似,使得粒子群很可能陷入局部最優(yōu)困境。鑒于此,本文將遺傳算法中的交叉、變異操作融入粒子群算法中,交叉操作體現(xiàn)粒子群算法中信息交換的思想,變異操作不但可以維持種群的多樣性,而且能夠減少早熟收斂現(xiàn)象的發(fā)生[13-15]。利用二者的優(yōu)勢(shì)互補(bǔ)性,本文提出一種混合粒子群(Hybrid Particle Swarm Opti-mization,HPSO)算法。
粒子位置和速度的交叉操作過(guò)程為:
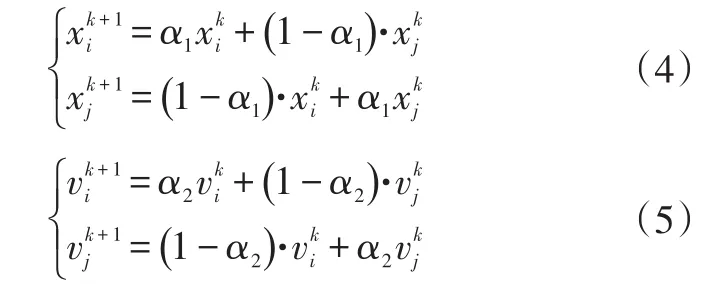
式中,α1、α2為[0,1]范圍內(nèi)的隨機(jī)數(shù);粒子分別為粒子進(jìn)行交叉操作后的子代粒子。
解的質(zhì)量依賴于變異率的選擇,本文采用隨機(jī)擾動(dòng)的方法對(duì)當(dāng)前個(gè)體極值pbest進(jìn)行高斯變異操作。對(duì)于每個(gè)粒子的當(dāng)前最優(yōu)極值,按照一定的概率pm實(shí)行變異,β服從gauss(0,1)分布,公式如下:
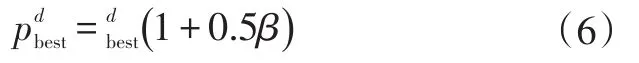
3.3 基于HPSO-BP神經(jīng)網(wǎng)絡(luò)的鋰電池SOC預(yù)測(cè)模型
鑒于HPSO算法具有收斂速度快、不易陷入局部極小的優(yōu)點(diǎn),可用于BP神經(jīng)網(wǎng)絡(luò)初始權(quán)值和閾值的優(yōu)化,本文基于HPSO-BP神經(jīng)網(wǎng)絡(luò)算法進(jìn)行鋰離子電池SOC的預(yù)測(cè)。HPSO-BP神經(jīng)網(wǎng)絡(luò)聯(lián)合算法流程為(見(jiàn)圖2):
a.根據(jù)輸入、輸出樣本集設(shè)計(jì)BP神經(jīng)網(wǎng)絡(luò)輸入層、隱含層和輸出層的神經(jīng)元個(gè)數(shù),確定網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu);
b.粒子群初始化,粒子群的大小取BP神經(jīng)網(wǎng)絡(luò)中所有權(quán)值w和閾值b的個(gè)數(shù)和,由于BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)設(shè)置為4-12-1,得到粒子維數(shù)d=4×12+12+12×1+1=73,學(xué)習(xí)因子c1、c2均設(shè)置為2,設(shè)定最大迭代次數(shù)itermax=300,誤差精度設(shè)定為0.001;
c.適應(yīng)度計(jì)算,根據(jù)適應(yīng)度函數(shù)計(jì)算各粒子的適應(yīng)度,確定每個(gè)粒子的個(gè)體最優(yōu)極值pbest和群體最優(yōu)極值gbest;
d.判斷算法是否達(dá)到終止條件(最大迭代次數(shù)或者誤差精度),如若滿足,則迭代結(jié)束,將最優(yōu)群體極值定為BP神經(jīng)網(wǎng)絡(luò)最優(yōu)初始權(quán)值閾值,進(jìn)行網(wǎng)絡(luò)訓(xùn)練與測(cè)試,否則進(jìn)入下一步迭代;
e.更新粒子群,按照式(1)和式(2)更新粒子速度和位置,并計(jì)算各粒子的適應(yīng)度,然后更新粒子的個(gè)體極值pbest和群體極值gbest;
f.個(gè)體、群體最優(yōu)粒子的交叉、變異操作,根據(jù)式(4)和式(5)完成粒子群位置和速度的交叉操作,然后根據(jù)式(6)完成變異操作;
g.采用輪盤賭法進(jìn)行最優(yōu)個(gè)體的保留與剔除。
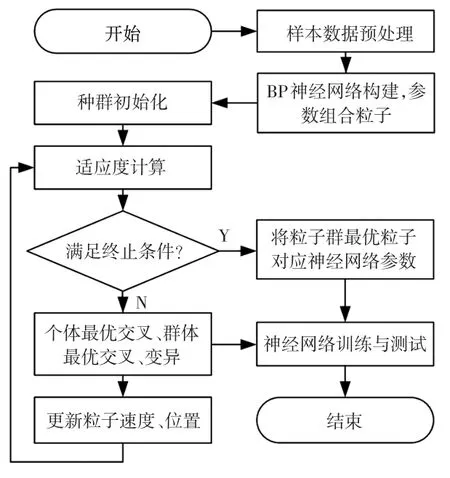
圖2 HPSO-BP神經(jīng)網(wǎng)絡(luò)聯(lián)合算法流程
4 仿真與結(jié)果分析
4.1 樣本數(shù)據(jù)選取
利用Neware公司的充放電測(cè)試儀記錄磷酸鐵鋰電池(4.2 V,1.75 A·h)的工作電壓、電流、溫度、內(nèi)阻和容量,從中提取580組數(shù)據(jù)作為樣本數(shù)據(jù),部分樣本數(shù)據(jù)如表1所示。
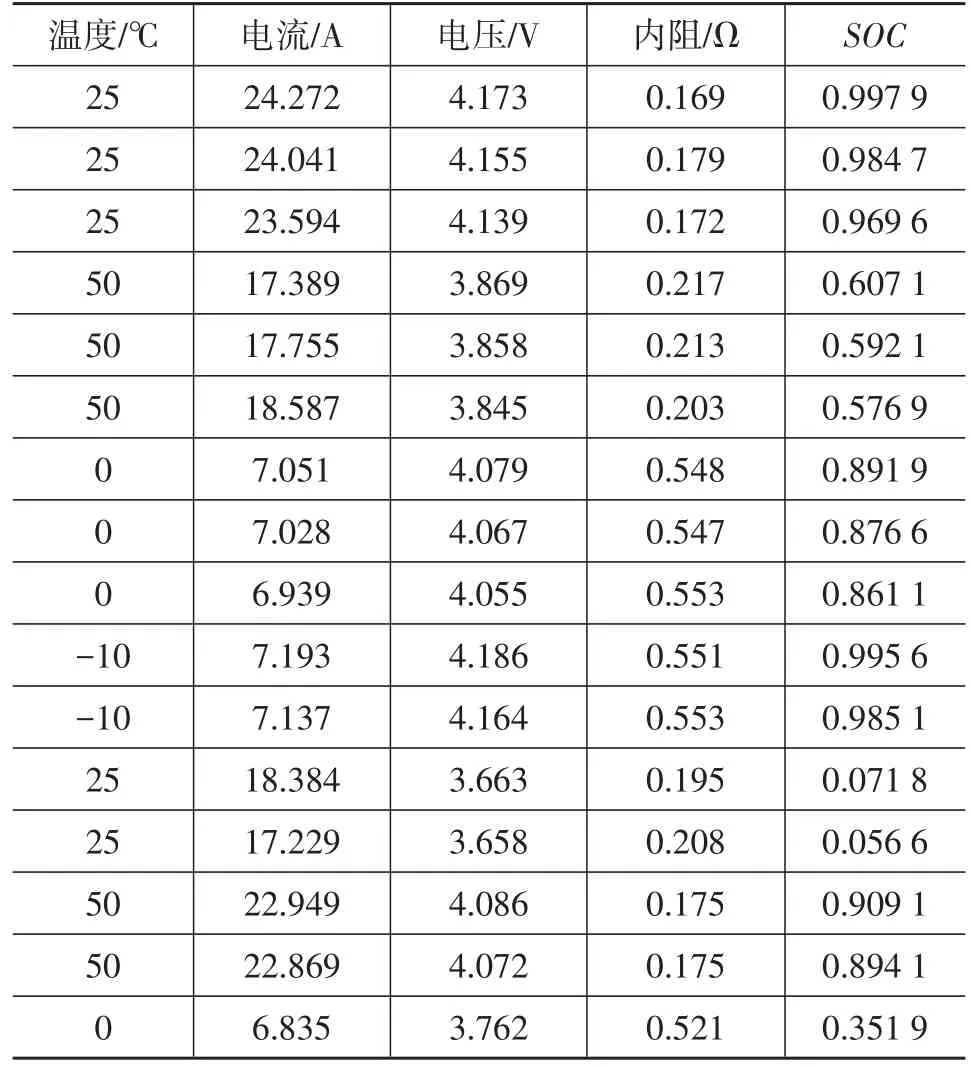
表1 部分樣本數(shù)據(jù)
由于本文BP神經(jīng)網(wǎng)絡(luò)中的激活函數(shù)為logsig函數(shù),故將上述樣本數(shù)據(jù)進(jìn)行歸一化處理:
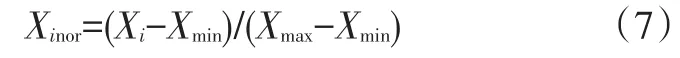
式中,Xi、Xinor分別為樣本值及其歸一化值;Xmin、Xmax分別為樣本數(shù)據(jù)中的最小值和最大值。
4.2 仿真與結(jié)果分析
為了驗(yàn)證HPSO-BP神經(jīng)網(wǎng)絡(luò)算法預(yù)測(cè)鋰電池SOC的準(zhǔn)確性和快速性,以BP神經(jīng)網(wǎng)絡(luò)均方根誤差(Root Mean Square Error,RMSE)作為適應(yīng)度評(píng)估函數(shù):
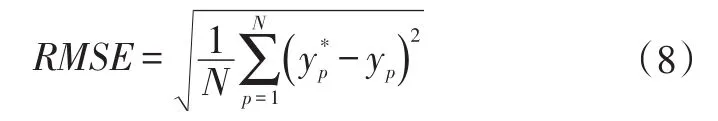
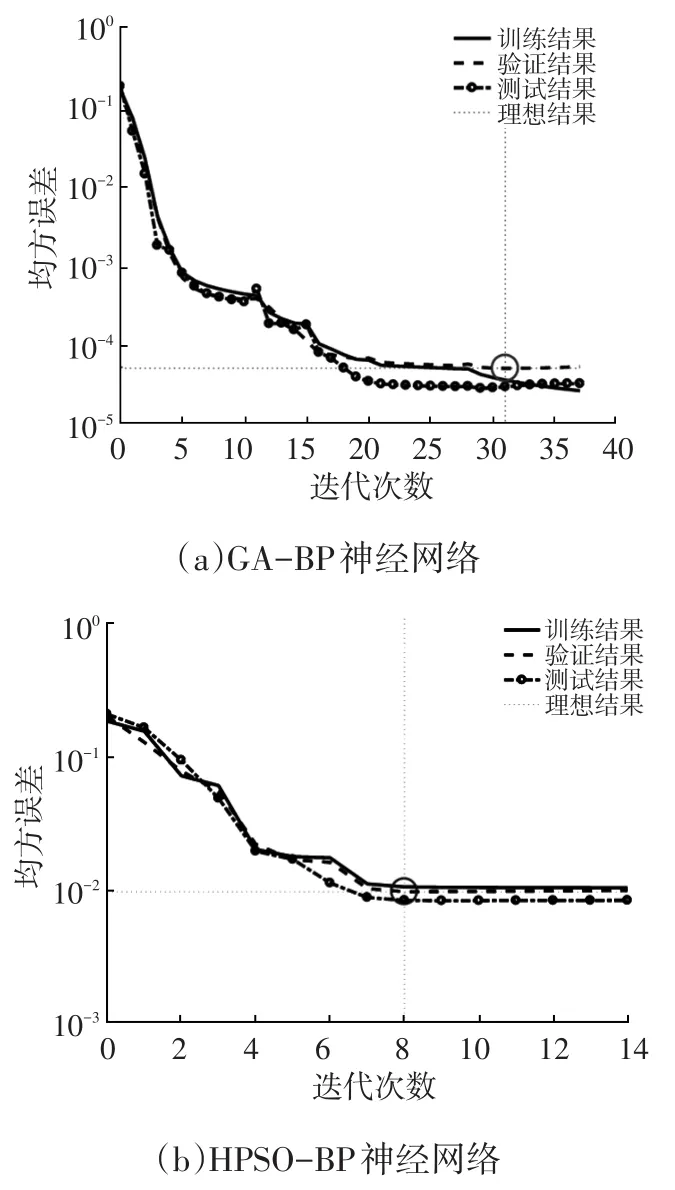
圖3 仿真誤差迭代曲線
從圖3a中可以看出,GA-BP神經(jīng)網(wǎng)絡(luò)在第32次迭代達(dá)到網(wǎng)絡(luò)設(shè)定精度,訓(xùn)練和驗(yàn)證迭代速度大致相同,測(cè)試速度相對(duì)較慢;圖3b中,HPSO-BP神經(jīng)網(wǎng)絡(luò)在第8次迭代就達(dá)到了網(wǎng)絡(luò)所設(shè)置的精度,并且迭代速度基本保持同步。通過(guò)對(duì)比可知,HPSO-BP神經(jīng)網(wǎng)絡(luò)表現(xiàn)出了更快的收斂速度。
圖4所示為網(wǎng)絡(luò)估算鋰電池SOC及其期望值。從圖4中可以看出,兩種網(wǎng)絡(luò)算法都取得了不錯(cuò)的預(yù)測(cè)效果,為了凸顯HPSO-BP神經(jīng)網(wǎng)絡(luò)算法預(yù)測(cè)鋰電池SOC的準(zhǔn)確性,繪制兩種網(wǎng)絡(luò)算法的誤差精度曲線如圖5所示。
從圖5中可以明顯看出:GA-BP神經(jīng)網(wǎng)絡(luò)算法的輸出結(jié)果誤差大部分保持在4%以內(nèi),最大誤差接近6%,達(dá)到了目前行業(yè)要求的低于8%的誤差精度;HPSO-BP神經(jīng)網(wǎng)絡(luò)算法的輸出結(jié)果誤差基本保持在2%以內(nèi),最大為3%,表現(xiàn)出了更高的估算精度。
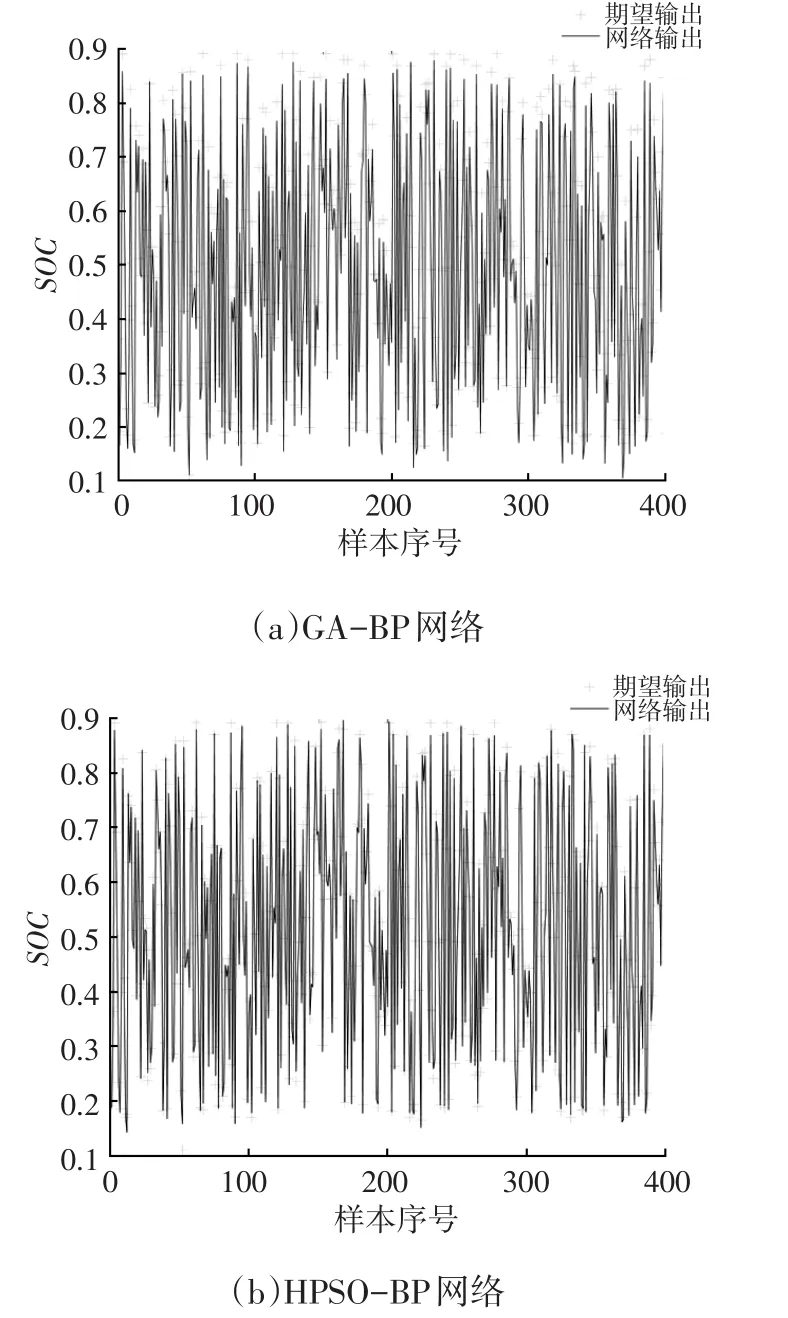
圖4 網(wǎng)絡(luò)輸出與期望輸出對(duì)比

圖5 網(wǎng)絡(luò)估算SOC誤差曲線
5 結(jié)束語(yǔ)
本文通過(guò)運(yùn)用改進(jìn)后的粒子群算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)初始權(quán)值閾值敏感、容易陷入局部極小值等缺點(diǎn),建立鋰離子電池荷電狀態(tài)估算模型,仿真結(jié)果表明,該聯(lián)合算法與傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)相比更具快速收斂性、準(zhǔn)確性和穩(wěn)定性。

