卷煙銷量組合預測模型研究

吳明山，王冰，起亞寧，鄭飄

1 河南中煙工業有限責任公司，河南省鄭州市鄭東新區榆林南路16號 450000;

2 國家煙草專賣局煙草經濟信息中心，北京市西城區月壇南街55號 100045

隨著卷煙營銷模式的不斷深化，卷煙市場逐步由“賣方市場”向“買方市場”轉變，消費者擁有越來越多的選擇權，對卷煙銷售工作的挑戰持續增加，銷量預測成為提升卷煙營銷水平的一項重要的內容。精準的卷煙預測，可有效消除卷煙供應鏈中的“牛鞭效應”，有利于煙草工商企業高度協同，提高企業對卷煙需求的把握能力，準確判斷需求變化趨勢，提升卷煙按訂單組織貨源水平，加快推動卷煙市場化取向改革。因此，提高卷煙銷量預測精度對提升卷煙營銷水平具有重大意義。

1 文獻綜述

傳統銷量預測方法有很多種，例如經驗分析、移動平均、指數平滑、線性回歸等[1]，可以一定程度上提高預測精度，這些方法對樣本數據本身有特定的要求（樣本量足夠大或線性相關），但在實際應用中產品銷售的歷史數據樣本量有限或不能完全滿足線性規律，預測效果會受到較大影響[2]。由于卷煙銷售受季節性和節日因素影響較大，呈現出明顯的季節性、周期性特征，其預測值往往與卷煙銷售歷史具有高度相關性，因此時間序列預測方法更加適合。ARIMA模型就是一種適合數據具有穩定的季節性特征的短期預測方法，具有較強的靈活性[3]，為季度或月度卷煙銷量預測，提供了較好的應用價值，預測結果較為可靠[4][5]。但由于其對數據穩定性要求較高，對于非穩定的時間序列的中長期預測精度有待提升。近年來，神經網絡模型因其靈活的非線性建模能力、較強的自適應性、學習能力和大規模并行計算能力，被廣泛地應用于時間序列預測研究中[6]。其中，BP神經網絡是應用最多的一種。理論證明，當隱含層神經元數目足夠多時,可以以任意精度逼近任何一個具有有限間斷點的非線性函數[7]，這一特性使其特別適合于求解內部機制復雜的問題，在銷量預測中受到廣泛關注。經典BP神經網絡算法是基于梯度下降的學習算法[8]，具有較強的自適應能力和容錯能力，但其收斂較慢、訓練時間較長，容易陷入局部最優，進而影響預測精度。因此，需要對該方法進行優化改進。基于Levenberg-Marquardt算法（LM算法）改進的BP神經網絡就是應用最廣泛的方法之一，該算法是用模型函數對待估參數向量在其鄰域內做線性近似，忽略掉二階以上的導數項，將優化目標方程轉化為線性最小二乘問題，并利用梯度求最值，同時具有梯度法和牛頓法的優點，預測效果得到進一步提升[9]。蔣興恒等采用基于LM算法改進的BP神經網絡對卷煙月度銷量進行預測，并與ARIMA預測結果進行比較，結果表明改進后的BP神經網絡模型預測效果更好[10]。

單項的預測模型具有各自的優缺點，只能提取數據的部分有效信息，且受設定條件的影響，預測精度仍有較大提升空間[11]。于是，J.M.Bates和C.W.J.Granger提出組合預測方法，該類模型能綜合提取不同預測方法的有效信息，它可以克服單一模型的局限性，預測精度得到有效提高[12]。因此，組合模型也開始應用于卷煙銷量預測中。朱俊江等通過建立小波變換、回歸分析和神經網絡算法構成的組合模型對鄉鎮單位的卷煙銷量進行預測，其預測精度要好于ARIMA模型和基于LM算法改進的BP神經網絡模型[13]。

組合預測模型的核心有兩個：一是單項預測模型的選擇，要根據數據的具體特征確定；二是確定各單項模型的權重，其方法可分為兩類：一類是固定權重，另一類是動態權重[14]。研究表明，動態權重組合模型比固定權重組合模型具有更高的預測精度[15]。因此，本文根據卷煙月度銷量數據非線性、波動性和規律性特征，選擇ARIMA模型、基于梯度下降算法的BP神經網絡模型、基于LM算法改進的BP神經網絡模型作為3個單項預測模型，并利用BP神經網絡對各單項預測模型進行動態加權，從而構建非線性組合預測模型，對2006～2017年144個月的全國卷煙銷量進行仿真訓練，綜合提取各單項預測模型的有效信息，以期預測2018年1～4月的全國卷煙銷量。

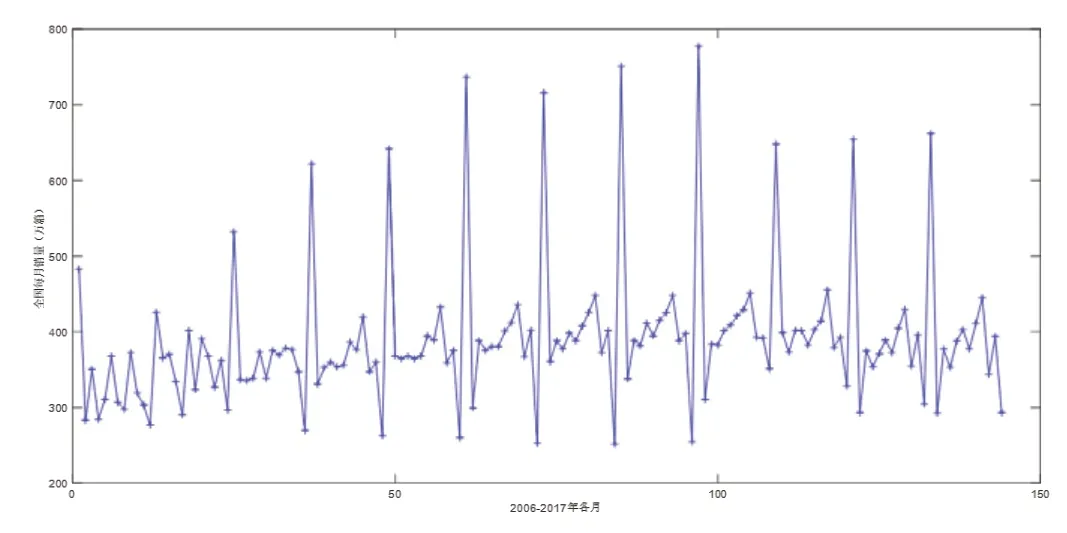
圖1 2006～2017年我國卷煙各月銷量趨勢Fig.1 Monthly sales trend of cigarettes in China from 2006 to 2017

2 卷煙銷量預測模型構建與預測

2.1 ARIMA模型

ARIMA模型是由Box和Jenkins提出的一種時間預測方法，該方法將原始時間序列數據看作一個隨機序列，并用一定的數學模型來近似描述，一旦被識別后，就可以利用該模型根據歷史數據來預測未來。本節以2006～2017年共144個月的全國卷煙銷量數據（萬箱）作為基礎數據，如圖1所示，應用MATLAB對其進行ARIMA擬合，并預測2018年1～4月的銷量。

2.1.1 數據處理

從銷量趨勢圖中可以看出，該時間序列非平穩，對數列先進行1階差分處理，將其平穩化，其公式為：

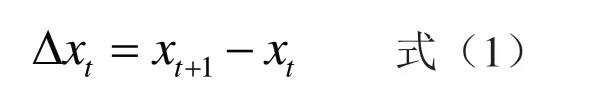
如圖2所示，一階差分的時間序列的均值和方差均基本平穩，接近一個白噪聲序列。

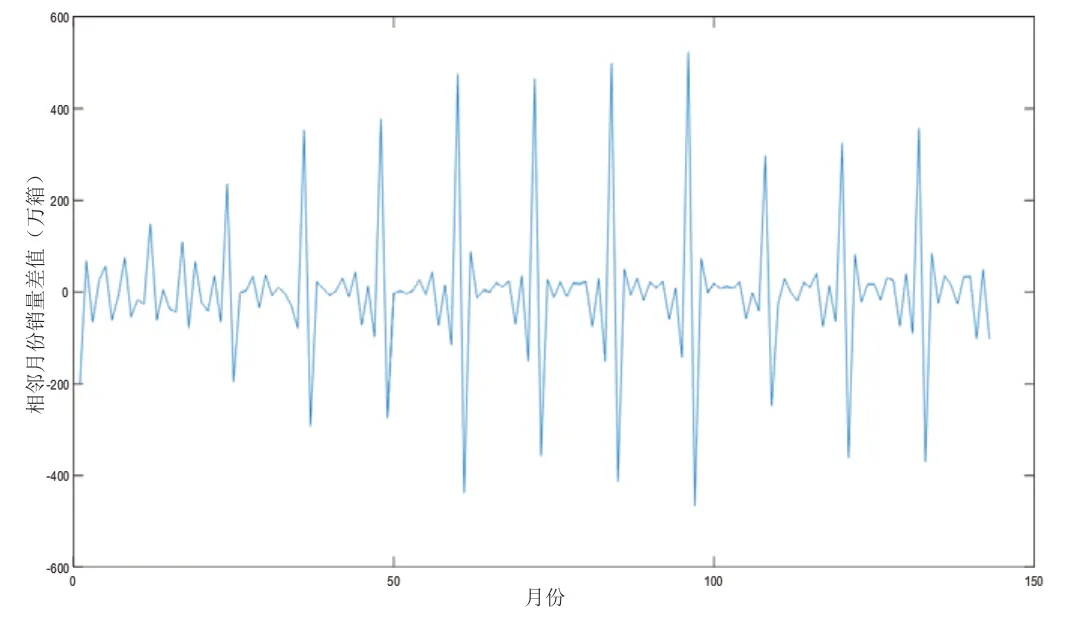
圖2 差分處理圖Fig.2 Differential processing diagram

圖3 自相關函數圖Fig.3 Autocorrelation function diagram

2.1.2 模型識別與定階

通過平穩性檢驗可知，即將建立的ARIMA（p，d，q）模型，其中d=1，其基本公式為：

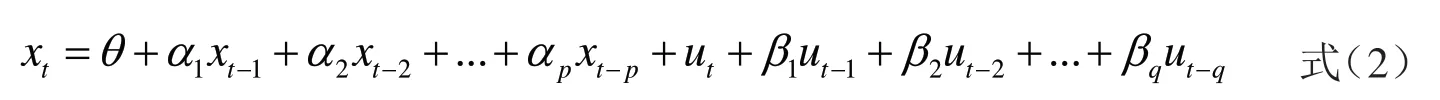
其中，x為時間序列，θ是常數項，α為自回歸系數，β為移動平均系數，μ為白噪聲，p為自回歸項，q為移動平均項。

為確認模型中p和q的值，以AIC準則為評價該時間序列數據的準則，利用MATLAB進行測試。本次基礎數據為144個，故將p和q的范圍定為1～29之間，通過測試確定AIC=7.06，p=25，q=7，即選擇的模型為ARIMA（25，1，7）。

2.1.3 仿真及預測結果

將p和q的值代入模型，計算得到2006～2017年各月卷煙銷量的擬合值（如圖4所示），模型擬合度為76.07%，平均絕對誤差為14.82，平均絕對誤差率（平均絕對誤差/平均真實銷量，下同）為3.81%，擬合精度整體良好。

將預測長度設定為4個月，利用該模型對2018年1～4月全國卷煙銷量進行預測，如表1所示，可以看出預測誤差均較大，除1月份外，其余3個月的絕對誤差值均大于當月的日均銷量。

2.2 基于梯度下降算法的BP神經網絡預測模型

BP神經網絡是 Rumelhart 和McClellend于 1986年提出一種多層網絡的“逆推”學習算法，是一種單向傳播的多層前向網絡，具有3層或3層以上，包括輸入層、隱含層和輸出層，其中隱含層可以有多個層次，上下層之間的神經元全部連接，但每層神經元之間相互獨立沒有連接，其結構如圖5所示。當學習樣本進入神經網絡后，神經元的激活值從輸入層經過各隱含層傳向輸出層，若達不到期望，則進入誤差反向傳播過程，逐次調整網絡各層的權值和偏置，最后回到輸入層，再重復計算，通過不斷調整各層的權值和閾值，從而達到網絡誤差最小，學習過程結束；再利用訓練好的網絡進行預測。

BP神經網絡通過訓練誤差來逐步調整各層間的輸入權重和偏置，這個調整過程的算法依據為最基本的梯度下降法（Gradient Descent），由于訓練誤差是關于輸入權重和偏置的二次函數，分別對權重和偏置求偏導數，即梯度向量，沿著梯度向量的方向，是訓練誤差增加最快的地方，而沿著梯度向量相反的方向，梯度減少最快，在這個方向上更容易找到訓練誤差函數（損失函數）的最小值。本節利用MATLAB軟件應用梯度下降算法的BP神經網絡對全國卷煙歷史銷量數據進行訓練并預測，其處理步驟如下：

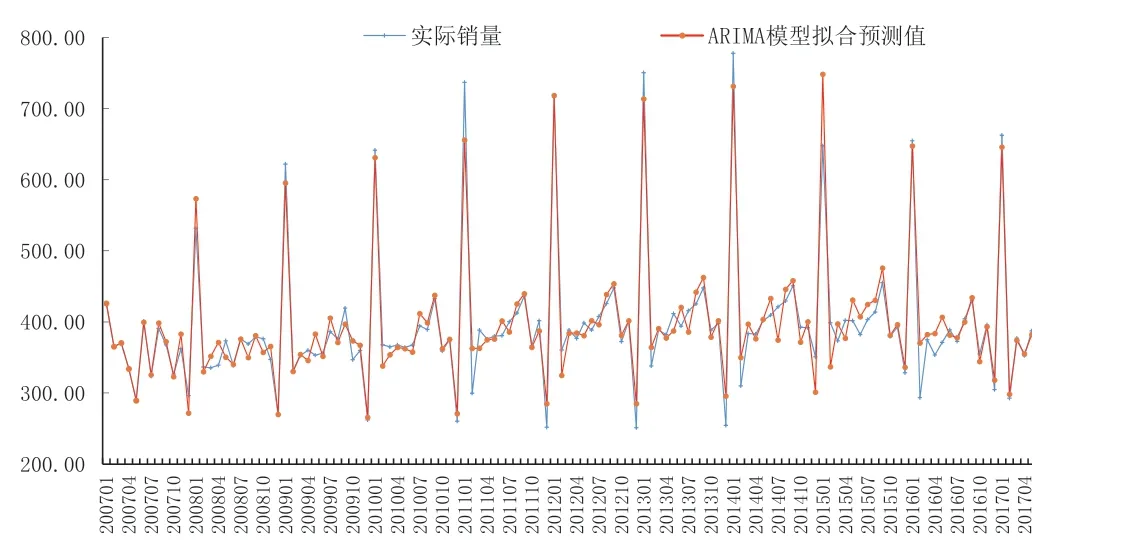
圖4 ARIMA模型對2006～2018年4月全國卷煙銷量的擬合及預測圖Fig.4 The fitting and forecasting of national cigarette sales from 2006 to April 2018 by ARIMA model

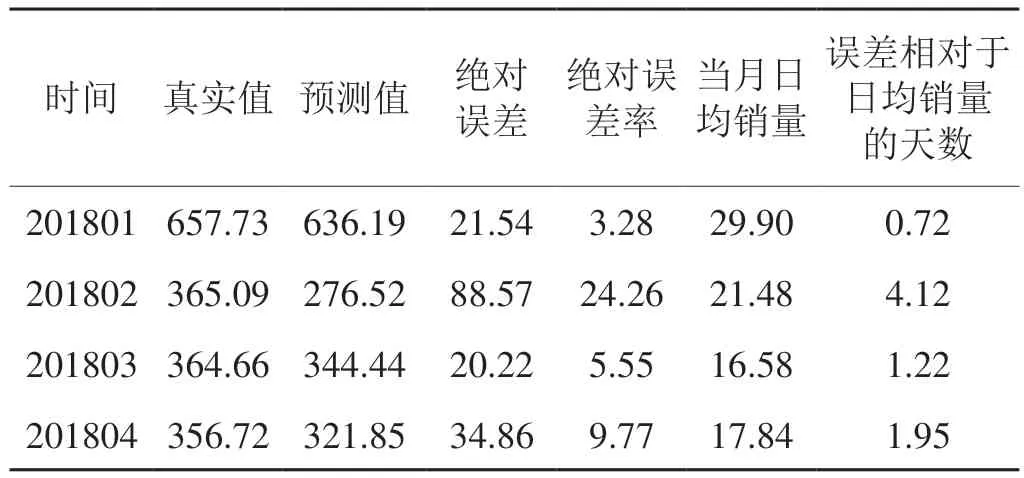
表1 ARIMA模型對2018年1～4月全國卷煙銷量預測表Tab.1 National cigarette sales forecast for January-April in 2018 by ARIMA model萬箱，%，天

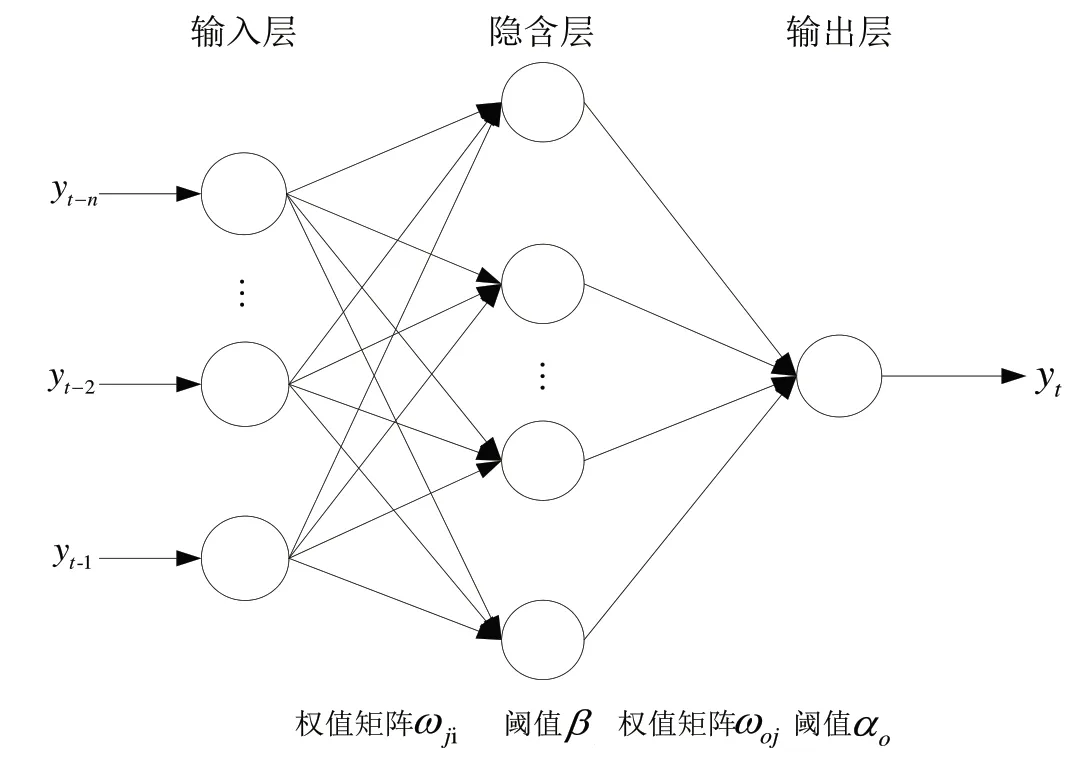
圖5 典型BP神經網絡模型結構Fig.5 Structure of typical BP neural network model structure

2.2.1 樣本數據確定

由于卷煙銷量執行的是年度計劃，為更好的反應卷煙銷量的時間特點，本文將2006至2017年每12個月銷量數據作為一組輸入向量，形成12*129的輸入矩陣；以之后4個月的銷量數據作為網絡的輸出，形成4*129的輸出矩陣，用神經網絡進行訓練。

2.2.2 樣本數據處理

數據的預處理和后處理是訓練神經網絡的關鍵步驟，它直接影響到訓練后神經網絡的性能，常見的方法是將原始數據進行歸一化處理，即通過一定的線性變換將輸入數據和輸出數據統一限制在[0,1]或[-1,1]區間內。本節選擇最大最小法進行處理，其函數形式是：

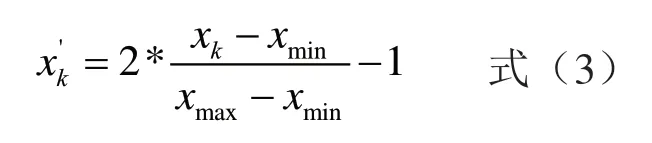
其中，xmin為數據序列的最小值，xmax為數據序列的最大值。最大最小值法可以通過MATLAB的mapminmax函數對數據進行處理，讓其落入在[-1,1]區間內。

2.2.3 創建網絡及參數設定

本模型設計主要涉及到網絡的層數、每層中的神經元個數和激活函數、初始值以及學習速率等幾個方面。

（1）網絡層數確定。理論證明，具有偏差和至少一個S型隱層加上一個線性輸出層的網絡，能夠逼近任何有理函數，增加層數可以進一步降低誤差，提高精度，但同時也使網絡復雜化。本節模型選擇3層網絡，即1個輸入層、1個隱含層、1個輸出層。

（2）創建網絡。在MATLAB中創建神經網絡要確定以下函數：①輸入層和隱含層的傳遞函數采用正切S型函數，以tansig表示，即：

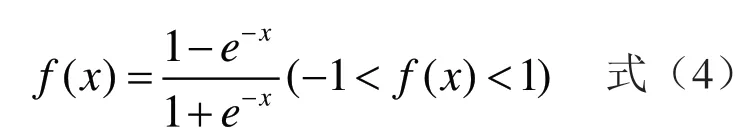
②輸出層的傳遞函數采用線性函數，以purelin表示；③網絡訓練函數采用動量反轉和動態自適應學習率的梯度下降算法訓練函數tianingd；④確定隱含層神經元個數，理論上沒有計算出多少隱含層節點最合適，在具體設計時，要通過對不同神經元數進行訓練比較，以網絡最小誤差為依據確定神經元數。通過循環計算，確定此模型的神經元個數為9個。

（3）網絡訓練參數設定。①根據梯度下降法的特點，訓練次數選取為80000；②誤差性能目標值選取為0.01；③學習速率一般取值范圍為0.01-0.8之間，學習速率太大可能導致系統的不穩定，但學習速率太小導致收斂太慢，需要較長的訓練時間，為達到目標誤差精度，此模型選取0.01。

2.2.4 仿真及預測結果

利用基于梯度下降算法的BP神經網絡預測模型對卷煙銷量數據進行訓練和仿真，如圖6所示，經過79976次訓練之后達到目標誤差0.01的要求，模型擬合效果如圖7所示，其平均絕對誤差為17.87，平均絕對誤差率為4.59%，其擬合精度不及ARIMA模型。

圖6 基于梯度下降算法的BP神經網絡訓練圖Fig.6 BP neural network training diagram based on gradient descent algorithm

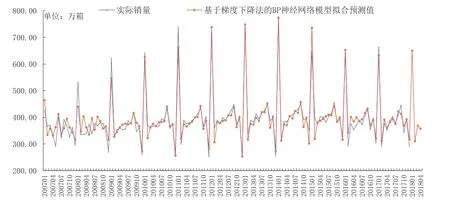
圖7 基于梯度下降算法的BP神經網絡對2007～2018年4月全國卷煙銷量的擬合及預測圖Fig.7 Fitting and forecasting of national cigarette sales from 2007 to April 2018 by BP neural network model based on gradient descent algorithm

輸入2017年12個月的卷煙銷量數據，模型得到2018年1～4月銷量的預測值，如表2所示，可以看出雖然該模型擬合效果不及ARIMA模型，但預測結果要明顯好于ARIMA模型，除2月份由于春節因素導致預測效果較差外，其余月份預測結果十分逼近真實銷量，均不足半天的當月卷煙銷量。

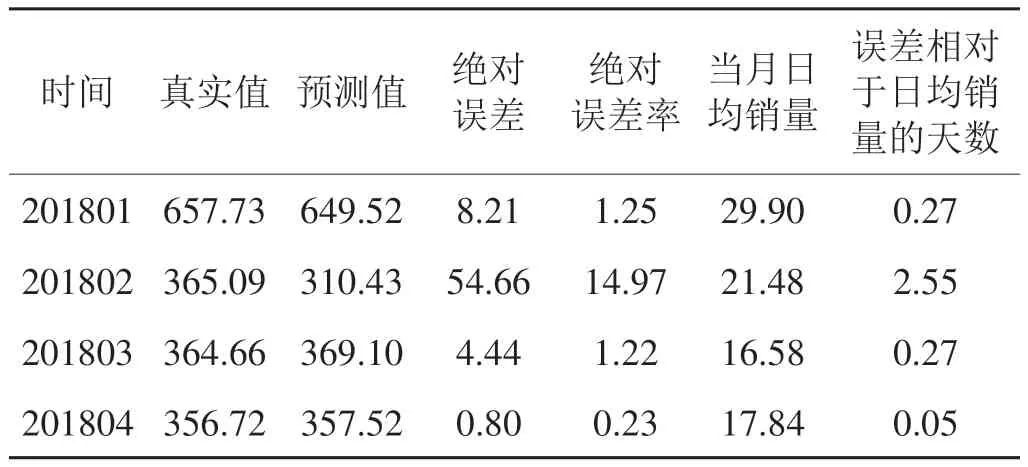
表2 基于梯度下降算法的BP神經網絡對2018年1～4月全國卷煙銷量預測表Tab.2 Forecasting of national cigarette sales volume from January to April in 2018 by BP neural network based on gradient descent algorithm萬箱，%，天

2.3 基于Levenberg-Marquardt算法改進BP神經網絡的預測模型

從上述基于梯度下降算法的BP神經網絡模型訓練過程發現，雖然該模型能較好的擬合卷煙銷量并比較準確的預測未來4個月的銷量，但其學習算法的收斂速度較慢，訓練次數達到了近8萬次，另外其預測誤差精度較低，僅能達到0.01。針對該模型存在的不足，出現了幾種基于該模型的改進算法，如擬牛頓法、Levenberg-Marquardt算法（簡稱LM算法）等。通過實驗發現，對中小規模的神經網絡，使用LM算法的收斂速度最快，且計算精度較高。作為BP神經網絡的改進算法，LM算法實際上是梯度下降法和高斯牛頓法的結合，該算法期望在不計算Hessian矩陣的情況下獲得高階的訓練速度，其公式表達為：

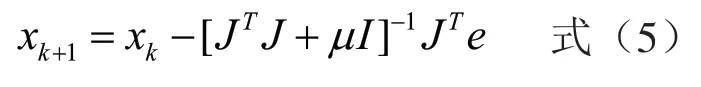
其中，J為雅克比矩陣，e是網絡誤差向量。隨著 越來越小，該算法越來越接近高斯牛頓法；隨著越來越大，該算法越來越接近梯度下降法。由于高斯牛頓法收斂速度更快更準確，因此LM算法的目的就是盡快接近高斯牛頓法，如果某次迭代成功，誤差減小，則減小 的值；如果迭代失敗，則增加 的值，從而使得誤差性能函數隨著迭代的進行而下降到極小值。

2.3.1 基于LM算法改進BP神經網絡模型構建

基于LM算法改進BP神經網絡模型的輸入向量和輸出向量與基于梯度下降算法的BP神經網絡模型相同，并進行歸一化的數據處理，確定網絡層數，選擇傳遞函數，設定訓練次數、訓練精度、學習速率等參數。但與前者不同的是，基于LM算法改進的BP神經網絡模型需要將模型的訓練函數更改成LM算法，在MATLAB中以trianlm表示。鑒于LM算法快速、準確收斂的特點，將模型訓練次數取為3000，誤差性能目標值取為0.0005，學習速率仍為0.01，經過測試神經元數量取為30個。

2.3.2 仿真及預測結果

利用LM算法改進BP神經網絡模型對卷煙銷量數據進行訓練和仿真，如圖8所示，經過32次即可達到目標誤差0.0005的要求，模型擬合效果明顯更好，如圖9所示。其平均絕對誤差為3.99，平均絕對誤差率為1.03%，其擬合精度明顯高于ARIMA模型和基于梯度下降算法的BP神經網絡模型。

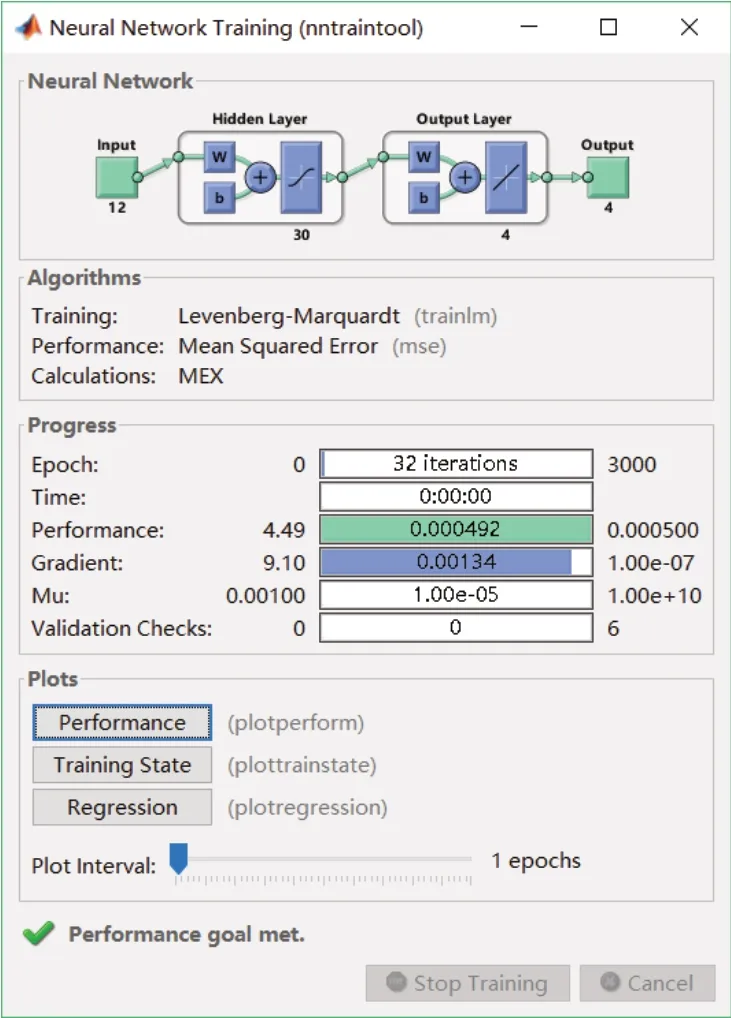
圖8 基于LM算法的BP神經網絡訓練圖Fig.8 BP neural network training diagram based on LM algorithm

輸入2017年12個月的卷煙銷量數據，從而得到2018年1～4月銷量的預測值，如表3所示，可以看出經過改進后的BP神經網絡模型，預測誤差更加均衡，其預測效果更加平穩，適應性更強。

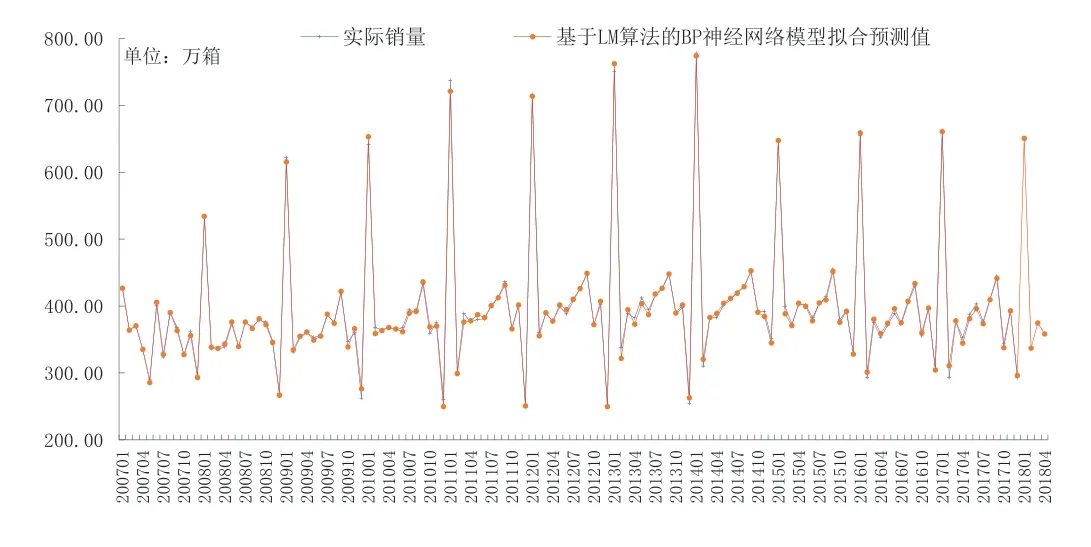
圖9 基于LM算法的BP神經網絡模型對2007 ～ 2018年4月全國卷煙銷量的擬合及預測圖Fig.9 Fitting and forecasting of national cigarette sales from 2007 to April 2018 by BP neural network model based on LM algorithm

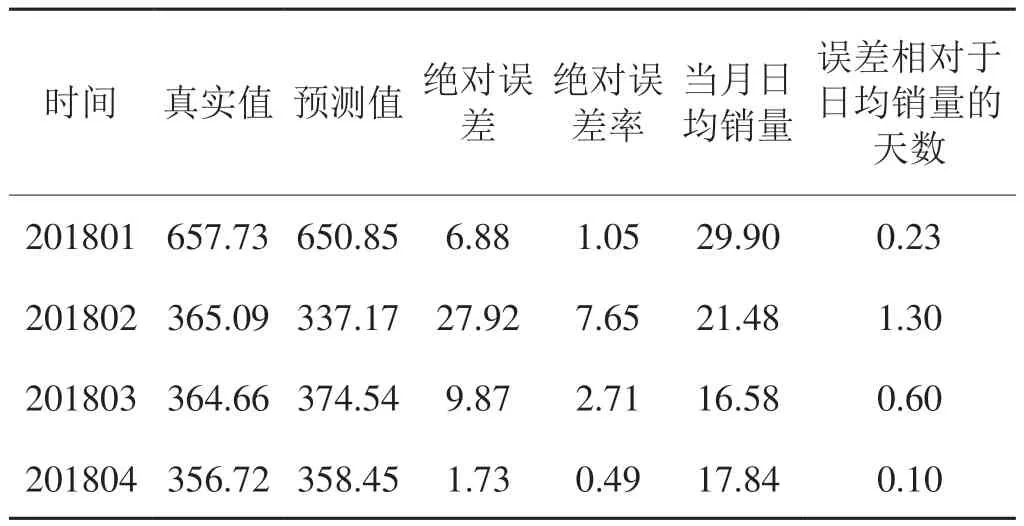
表3 基于LM算法的BP神經網絡模型對2018年1 ～ 4月全國卷煙銷量預測表Tab.3 Forecasting of national cigarette sales forecast for January-April in 2018 by BP neural network model based on LM algorithm萬箱，%，天

2.4 非線性組合預測模型構建與預測

上述3種模型均在一定程度上解釋了卷煙銷量數據之間的聯系，并對未來4個月的卷煙銷量進行預測，但單項預測方法存在未能充分利用歷史數據的缺點，從而導致預測結果不夠精準，為此，通過構建非線性組合預測模型，吸收各模型的優點，提高預測精度。

2.4.1 模型構建思路

本節通過基于LM算法改進的BP神經網絡構造非線性組合模型，其構建思路為：（1）以ARIMA模型擬合值、基于梯度下降算法的BP神經網絡擬合值、基于LM算法的BP神經網絡擬合值作為輸入向量，即選取相同月份的3種模型擬合值作為輸入向量，當月真實銷量作為輸出向量，進行訓練后進行仿真擬合；（2）輸入上述3種模型對2018年1～4月全國卷煙銷量的預測值，得到組合預測模型對銷量的預測結果。

2.4.2 模型參數設定

對銷量數據的訓練參數設定為：訓練次數取為3000，誤差性能目標值取為0.0005，學習速率為0.01，經過測試神經元數量取為30個。

2.4.3 仿真及預測結果

通過訓練，組合預測模型訓練的銷量數據經過4次達到目標誤差精度0.0005的要求，如圖10所示，模型擬合效果明顯更好，如圖11所示。其平均絕對誤差為3.3，平均絕對誤差率為0.85%，其擬合精度均高于上述3種模型。

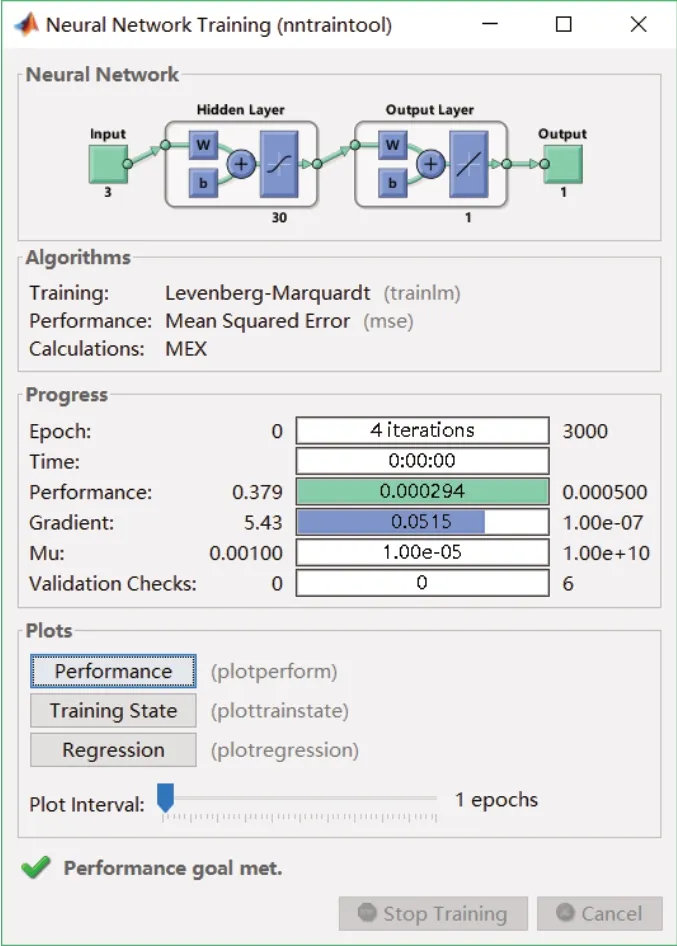
圖10 組合預測模型的銷量數據訓練圖Fig.10 Sales data training chart of combined forecasting model

圖11 非線性組合預測模型對2007～2018年4月全國卷煙銷量的擬合及預測圖Fig.11 Fitting and forecasting of national cigarette sales from 2007 to April 2018 by nonlinear combination forecasting model

輸入上述3種模型對2018年1～4月銷量的預測值，利用訓練好的模型得到組合預測模型對2018年1～4月銷量的預測值，如表4所示，可以看出組合預測模型的預測絕對誤差較為均衡，均不足1天的當月日均銷量。

2.5 模型預測效果對比

對比4種模型的預測值，發現各預測模型呈現不同的特點：ARIMA模型預測近期銷量相對較準，但較遠月份的預測值誤差較大；基于梯度下降算法的BP神經網絡模型可以較為準確的預測大部分月份的卷煙銷量，但對于波動性較大的月份預測誤差較大；基于LM算法的BP神經網絡模型作為改進后的神經網絡模型，預測結果精度更高，預測誤差更為平穩；非線性組合預測模型綜合利用上述3種模型的優點，有效提取數據各方面信息，預測絕對誤差均小于當月的日均量，其預測結果最為平穩，適應性最強，更加貼合卷煙銷售實際情況。

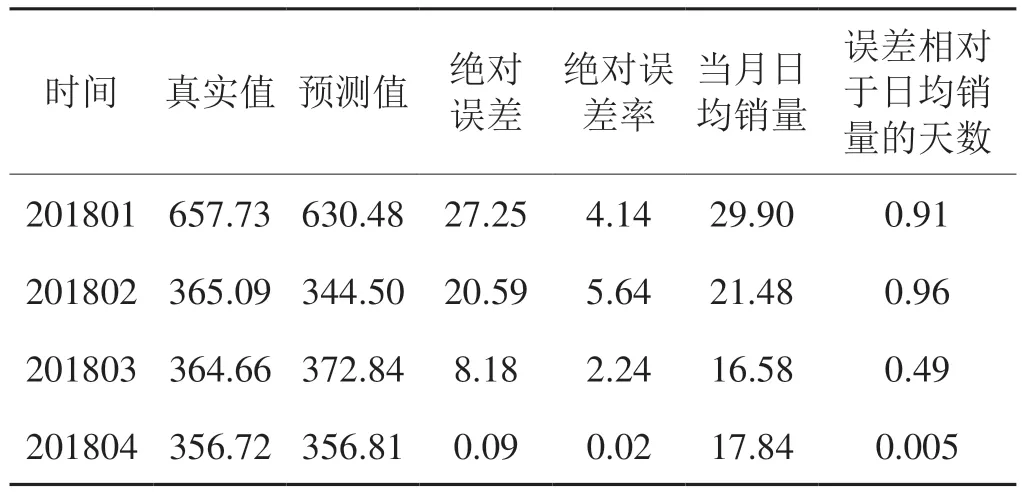
表4 非線性組合預測模型對2018年1～4月全國卷煙銷量預測表Tab.4 Forecasting of the national cigarette sales from January to April in 2018 by nonlinear combination forecasting model萬箱，%，天

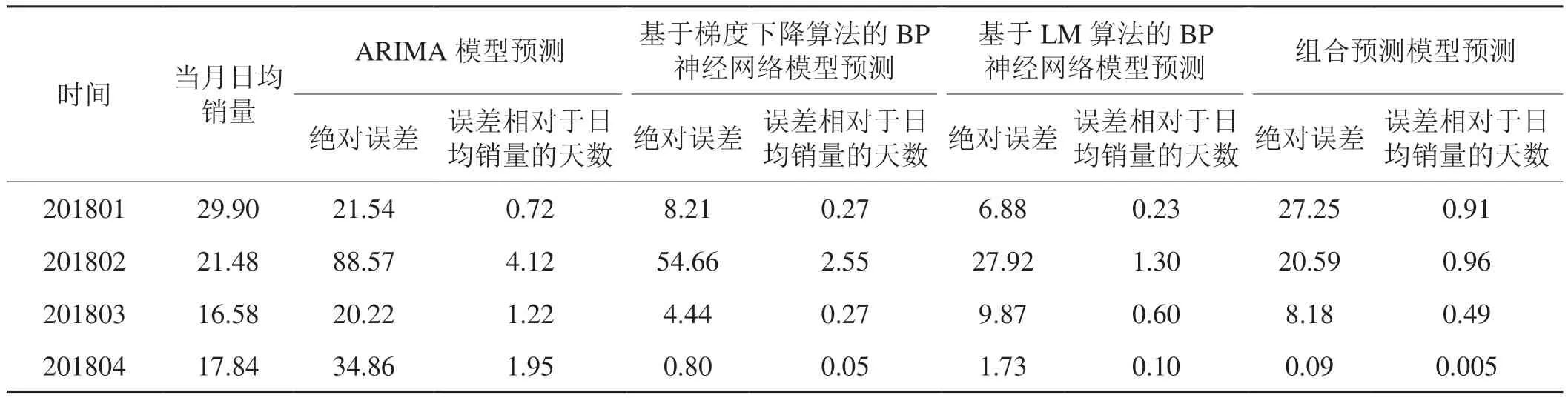
表5 四種模型對2018年1～4月全國卷煙銷量誤差值對比Tab.5 Comparison of error values of national cigarette sales from January to April in 2018 by four different models 萬箱，天

3 結論

本文選擇ARIMA模型、基于梯度下降算法的BP神經網絡模型、基于LM算法改進的BP神經網絡模型作為3個單項預測模型，并利用BP神經網絡對各單項預測模型進行動態加權，從而構建非線性組合預測模型，對2006～2017年144個月的全國卷煙銷量進行仿真訓練，并對2018年1～4月的卷煙銷量進行預測。通過對比表明，非線性組合模型具有更好的預測效果，對卷煙調撥計劃制定，科學安排生產計劃等具有一定的參考意義。此外，該模型的構建思路還可用于卷煙各價類的銷售預測。

同時，在研究過程中，發現由于春節及政策的影響，每年1月份的卷煙銷量遠高于其他月份，2月份銷量迅速下降，致使1、2月份的差值非常大，數據極具波動性，極易造成預測誤差。因此，后續研究中，可以引入月度調節因子、政策影響因子等調整因素，以期進一步提高預測精度。