UHPC薄板屈曲試驗及臨界板厚比研究

吳延偉

(中鐵第一勘察設計院集團有限公司，西安 710043)

1 概述

超高性能混凝土UHPC(Ultra-high Performance Concrete)是一種具有高強度力學性能的混凝土材料，該材料在鐵路橋梁工程中主要應用于人行道板、道砟槽板等，橋梁主體受力結構采用UHPC材料建造的工程實例較少，該材料應用的深度和廣度有待提高。

為了促進UHPC在橋梁主體受力結構的應用，國內外學者進行了一系列的理論研究和試驗研究。張哲[1]等開展了超高性能混凝土軸拉性能試驗研究，研究表明鋼纖維的形狀和摻量是影響UHPC材料初裂應變的關鍵因素等。曹霞[2]等開展了不同縱筋率高強鋼筋RPC梁抗剪承載力及剪切延性試驗研究，研究表明高強鋼筋RPC梁正常使用極限狀態下最大裂縫寬度不超過0.3 mm、梁截面應變符合平截面假定、并擬合出高強鋼筋超高性能混凝土梁抗剪承載力經驗公式等；孫明德[3-4]等開展了高強鋼筋活性粉末混凝土梁抗彎性能試驗研究和高強鋼筋與活性粉末混凝土粘結性能試驗研究，研究表明RPC適筋梁正截面破壞過程與普通混凝土梁相似、提出鋼筋與RPC之間的粘結長度和最小保護層要求等。劉琛[5]研究了鐵路大跨度活性粉末混凝土簡支梁截面形式，提出活性粉末混凝土和普通混凝土組合結構截面，并指出RPC梁多為細長柱結構，設計階段應進行穩定性分析。李志光[6]、金凌志[7]、徐海賓等[8-16]還進行了活性粉末混凝土橋梁其他關鍵技術問題的研究。總之，針對UHPC結構的軸拉、抗彎、抗剪等試驗研究已取得一定的研究成果，而UHPC橋梁屈曲問題仍停留在理論計算階段，屈曲試驗研究較為欠缺。

與普通混凝土相比，UHPC材料更優，構件尺寸設計可以更加纖細[17]。因此，UHPC作為高強度的力學材料，在鐵路簡支箱梁設計時必然采用薄壁形結構，UHPC橋梁設計不僅需要考慮結構的整體穩定，還需考慮組成箱形截面的懸臂板、腹板間頂板和腹板的局部失穩問題[18]。本文通過19個UHPC薄板試件屈曲試驗，研究其局部失穩破壞特征，提出UHPC薄板屈曲承載力影響因素及不同邊界條件下UHPC板的臨界板厚比。

2 UHPC薄板試驗

2.1 試驗構件及試驗板制作

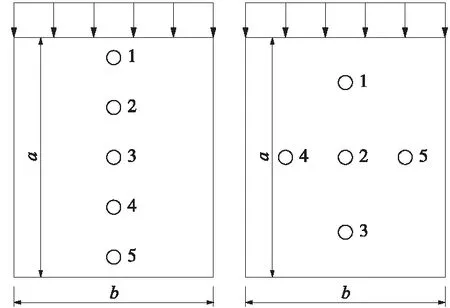
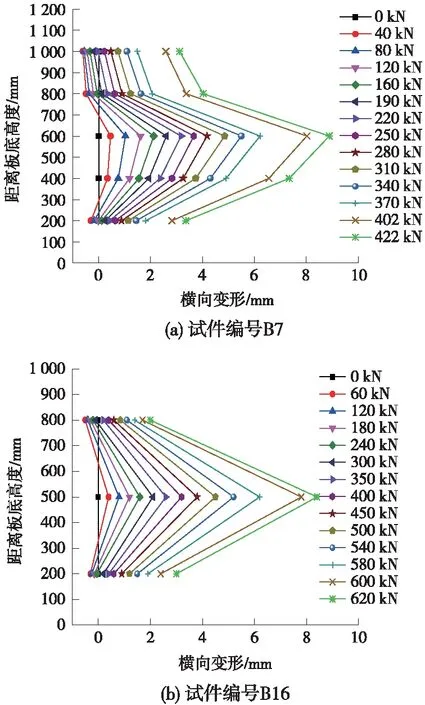
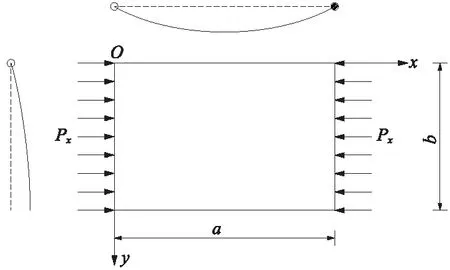
板按照其厚度可分為厚板、薄板和薄膜3種。將板的厚度t與板幅面的最小寬度b相比，當(1∶80～1∶100)

UHPC試驗板均為矩形薄板，板的高厚比、寬厚比和邊界條件為主要變化參數，板的厚度均為26 mm，高厚比30.8～46.2，寬厚比21.2～42.3，共19個試件，邊界條件為四邊簡支、兩邊簡支兩邊自由、兩邊固定兩邊自由。試件制作配合比見表1，試驗板的UHPC立方體強度為120 MPa，彈模為46 GPa。養護制度為40 ℃蒸汽養護24 h后拆模，再進行75 ℃蒸汽養護48 h，靜置7 d后進行加載試驗。

表1 UHPC薄板試件配合比

2.2 試驗裝置及測試方案

UHPC矩形板的加載方案見圖1，當板的側邊無約束時，沿著板的豎軸中心線上均勻布置5個位移計，見圖2；其他邊界條件時，在板中心、橫軸中心線和豎軸中心線布置5個位移計，呈十字形，見圖2。試驗參照GB/T 50152—2012《混凝土結構試驗方法標準》進行，數據采集采用DH3816靜態應變儀，記錄每級荷載下的水平位移和UHPC板的破壞情況。

圖1 UHPC板加載示意

圖2 位移計測點布置

3 試驗結果與分析

3.1 UHPC板的破壞形態及屈曲荷載

板的破壞形態有3種：一是板頂端或者底部局部受壓破壞，如圖3(a)；二是板的單方向裂縫行為，當板的寬度較窄時，在板的豎向產生3條橫向裂縫，如圖3(b)，板較寬時，在板的中間產生1條裂縫，如圖3(c)；三是雙向裂縫行為，板在豎向和橫向產生了雙向曲率裂縫破壞模式，裂縫都是完全對稱的，如圖3(d)和圖3(e)；單方向行為和雙向行為的板都是突然破壞，脆性斷裂，且在斷裂時產生爆炸式巨響。屈曲試驗結果見表2。

從表2可知：①屈曲承載力隨高厚比的增加而減小，當高厚比由38.5變化到46.2時，屈曲承載力降低了16.3%；②屈曲承載力隨著寬厚比的增大而增大；③不同邊界條件試驗表明：在高厚比、寬厚比相同時，非加載邊兩邊自由、一邊簡支一邊自由和兩邊簡支時的屈曲承載力為P兩邊自由

圖3 UHPC薄板破壞形式

非加載邊邊界條件兩邊自由兩邊自由兩邊自由兩邊自由兩邊自由兩邊簡支一邊簡支一邊自由編號a/mmb/mm高厚比寬厚比B1900110034.642.3B21000110038.542.3B31000110038.542.3B41000110038.542.3B51200110046.242.3B61200110046.242.3B71200110046.242.3B8120074046.228.5B9120074046.228.5B10120074046.228.5B11120055046.221.2B12120055046.221.2B13120055046.221.2B141000110038.542.3B151000110038.542.3B161000110038.542.3B171000110038.542.3B181000110038.542.3B191000110038.542.3屈曲承載力/kN680.7平均520.5平均447.6平均310.5平均223.8平均637.1平均610.4

3.2 屈曲荷載計算

利用MIDAS軟件建立UHPC矩形板的有限元模型，以B15板為例，施加荷載110 kN，程序計算局部失穩荷載系數為5.12，即B15板的理論計算屈曲荷載為563.2 kN，見圖4。試驗板理論計算與試驗數據對比見表3，由表3可知：試驗值與計算值比值為0.69～1.13，考慮到UHPC材料均一性及制作初始缺陷等因素的影響，試驗值與計算值基本吻合。偏于安全起見，UHPC板屈曲承載力計算時應取折減系數0.7。

圖4 有限元計算模型及結果(試件編號B15)

邊界條件試驗板編號屈曲承載力/kN試驗值計算值試驗值/計算值兩邊自由B2～B4520.5574.20.91兩邊簡支B14～B16637.1563.21.131邊簡支1邊自由B17～B19610.4885.50.69

3.3 UHPC板屈曲荷載變形曲線

沿UHPC試驗板的垂直中心線的荷載-法向位移曲線見圖5。其中B7板邊界條件為兩邊自由，B16板邊界條件為兩邊簡支。根據試驗測試結果，試件在加載初期變形不明顯，隨著荷載增加，由于加載的初始偏心和試驗板澆筑制作時的初始缺陷，UHPC板在一個方向產生彎曲變形，隨著荷載的增加，產生的法向位移逐漸增大，繼續加載直到板發生破壞，法向位移的最大幅值大多出現在板的1/2高度位置。

圖5 豎向垂直線的橫向變形

屈曲承載力的判斷準則：在荷載作用下板的平衡狀態開始喪失穩定，稍有擾動則變形迅速增大，最后結構破壞。板在同級荷載加載下，法向變形增大的幅度很大時的荷載即為屈曲承載力，如圖B7板的屈曲荷載為422 kN，B16板的屈曲荷載為620 kN。所有UHPC板只在一個方向產生變形，即只產生一個半波。B5～B7板實測平均屈曲承載力為447.6 kN，B14～B16板實測平均屈曲承載力為637.1 kN。

4 臨界板厚比

鐵路UHPC橋梁一般采用箱形截面[5]，箱梁底板和腹板一般布置有預應力鋼束，底板和腹板因鋼束波紋管對于構造的控制而板厚比較小，且底板和腹板的壓應力水平通常較低，因此難以發生局部失穩。 UHPC箱梁的頂板通常承受較大的壓應力且板厚較大，易發生局部失穩破壞。箱梁的腹板間頂板計算模型為兩邊簡支板，見圖6。箱梁的懸臂板計算模型為一邊簡支一邊自由板，見圖7。

圖6 單向均勻受壓兩邊簡支板

圖7 均勻受壓一邊簡支一邊自由板

當局部失穩狀態下的歐拉應力σcr大于材料屈服應力fy，則理論上受壓板件彈性穩定不控制設計，結構強度破壞早于失穩破壞。對于混凝土和鋼構件，一般要求彈性穩定安全系數不小于4[20]，按照一般混凝土構件允許應力約為混凝土軸心抗壓強度的0.5倍考慮，即歐拉應力σcr大于UHPC軸心抗壓強度的2倍時，板件局部失穩不控制設計。對于本試驗120 MPa級UHPC材料，其軸心抗壓強度由試驗得出為87.6 MPa[21]，其屈曲失穩歐拉應力σcr為175.2 MPa。屈曲失穩歐拉應力σcr計算公式如下[22]

式中，k為屈曲系數，根據非加載邊的支承條件類型取值見表4；E為UHPC的彈性模量，試驗實測值為46 GPa；泊松比ν為0.3；b和t分別為板的寬度和厚度。

將歐拉應力175.2 MPa代入公式，計算不同邊界條件下的板厚比見表4。

表4 加載邊簡支時單項均勻受壓板的屈曲系數

5 結論

(1)UHPC薄板的屈曲形態主要有3種：①板頂端或者底部局部受壓破壞；②板的單方向裂縫行為，板較窄時，在板的豎向產生3條橫向裂縫，板較寬時，在板的中間產生1條裂縫；③雙向裂縫行為，板在豎向和橫向產生了雙向曲率裂縫破壞模式，裂縫都是完全對稱的。

(2)屈曲荷載試驗值和理論計算值的誤差在0.69～1.13，兩值基本吻合。考慮到UHPC材料、制作等因素的影響，UHPC板屈曲承載力計算時應取折減系數0.7。

(3)UHPC板法向位移的最大幅值大多出現在板的1/2高度位置，本試驗UHPC所有板件只在一個方向產生變形，即只產生一個半波。

(4)UHPC板屈曲荷載及失穩時臨界應力可根據歐拉公式計算，歐拉應力可為UHPC軸心抗壓強度實測值的2倍，由此推導板的臨界板厚比。箱梁腹板間頂板最小板厚比為30.8，箱梁懸臂板的最小板厚比為10.0，最小板厚比不足時應增加UHPC板厚度或采取加勁措施滿足穩定性要求，避免失穩破壞先于強度破壞。