基于FP-tree與云變換的圍巖穩定性評價指標體系研究

薛黎明，李長明，鄭志學，孟 碩，王 恩，王豪杰

(1.中國礦業大學(北京)資源與安全工程學院，北京 100083； 2.北京大學工學院，北京 100871)

隨著我國社會經濟的迅速發展，抽水儲能電站、鐵路隧道和大型水力發電站等地下工程建設越來越傾向規模化與大型化，各種地質災害、安全隱患也隨之增加[1-2]，為了確保地下工程的安全，必須對圍巖進行準確分類。圍巖穩定性等級主要用于確定合理和經濟的支護方案，并為地下工程的選址提供依據。

目前，圍巖分級的普遍方法是RQD[3]、Q分類法[4]及國內的《工程巖體分級標準》[5]，上述分類方法并沒有區分各指標在分級中的主次關系，且根據觀測數據求得的函數多采用回歸分析等簡單線性關系，得出的結果與實際情況具有一定差異。圍巖穩定性系統是高度復雜的非線性的動態系統，難以應用傳統實驗方法對其穩定性進行分析判斷[6]。近年來隨著計算機技術和現代應用數學理論的發展，可拓模型、PSO-PP(粒子群優化投影尋蹤模型)、一維云模型、神經網絡[7-12]等廣泛應用于圍巖分級中，并在實踐中取得了一定成果。

上述方法中的核心是選取合適的指標體系作為圍巖穩定性分級標準，目前，圍巖穩定性分級沒有統一的標準，不同的分級標準的形式和意義差異較大。現階段地下工程施工密集，相鄰工程影響較大，巖體受擾動較大，傳統指標體系難以適用于現階段的地下工程的特點，所以急需建立一套新指標體系對圍巖進行準確分級。在確定圍巖穩定性指標時，學者通常根據經驗法、聚焦法和統計學方法[13-15]確定圍巖穩定性的指標，但經驗法和聚焦法易受學者的思維限制而導致受主觀影響較大，難以滿足評價指標選取的全面性和相關性的原則；統計學方法在對指標結構優化時計算復雜，指標的相關性難以確定。對此，本文采用FP-tree(頻繁模式樹)對大量的圍巖穩定性分級體系進行挖掘得到頻繁項集，即為新的圍巖穩定性體系。該方法充分利用前人經驗，并通過相關性分析，使指標選取更加合理。圍巖穩定性分級指標確定后，采用云變換理論確定各指標的等級閾值，實現了分級標準的“軟劃分”同時兼顧了分級的模糊性，使分級標準更符合工程實際，避免了以往的指標分級標準邊界過硬，無法反映數據的分布特征。本文通過FP-tree和云變換確定圍巖穩定性的分級標準，為圍巖穩定性指標體系的建立提供一種新方法。

1 FP-tree及云變換理論

1.1 FP-tree理論

FP-tree算法[16]是關聯規則挖掘最常用算法之一，將提供的項目集進行壓縮，形成一棵保持關聯信息的頻繁模式樹，通過頻繁模式樹的數據結構對數據進行搜索，最終確定最大頻繁集項。FP-tree算法是在Apriori算法的基礎上進行改進的，避免產生大量的候選短頻繁項，且減小掃描時間，因此在數據挖掘上具有廣泛的應用，其FP-tree的算法過程如下。

(1)對數據庫C中的元素l進行第一次挖掘，記錄頻次并排序，得到候選頻繁項集。

(2)設立最小支持度，刪除小于最小支持度的元素，生成頻繁項集。

(3)重新生成數據庫，并進行重復掃描建立FP-tree。

(4)建立索引表，得到最大頻繁項集Ci=(li…lk)。

1.2 云變換

云變換[17]將論域的實際數據分布轉化為概念分布，實質為數值型屬性的定義域轉化為若干個云模型來表示，即對不規則的數據分布進行數學變換，成為若干個云模型進行相互疊加，其數學表達式為

(1)

式中,g(x)為數據分布；fj(x)為云期望函數；Cj為系數；m為云疊加個數；ξ為最大誤差。

云變換的核心是對fj(x)函數的求解，即得到不同等級的數字特征期望(Exj)、熵(Enj)和超熵(Hej)，進而構造等級云圖。由于圍巖數據在理論上是無窮多的，且不同區域之間圍巖數據是互相獨立的，在數學上已經證明，實際中很多現象均符合正態分布，同時正態分布也是其他分布的極限分布[18]。同時本文將正態分布引入超熵的概念，形成正態云模型，拓寬了正態分布的適用條件，使指標更為準確，故將指標數據的正態分布劃分為若干個云圖，通常劃分為5個等級，如圖1所示。

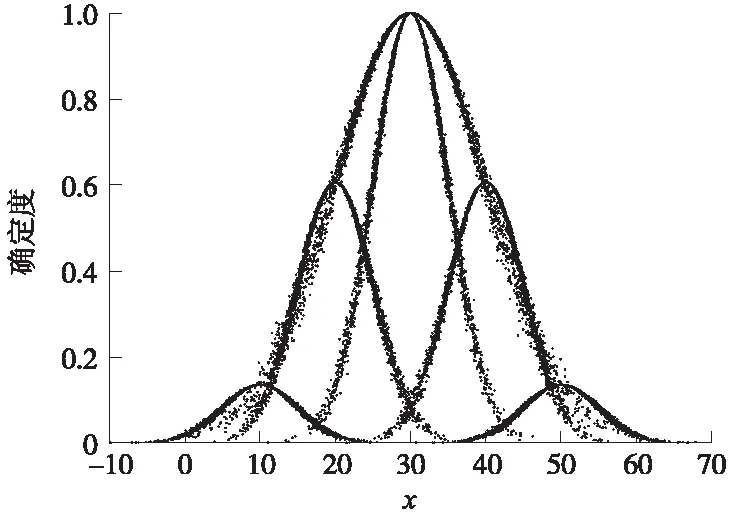
圖1 云概念劃分

圖1中的綜合圖形表示數據分布的實際情況，可以變換為若干個云模型相互疊加的形式，其中通過原始數據和逆向云發生器確定中間云的數字特征(Ex0，En0，He0)，其逆向云發生器算法如下。

(1)計算xi的平均值，Ex=MEAN(xi)，求得期望值Ex；

(2)計算xi的標準差，En=STDEV(xi)，求得熵En；

(3)對每一數對(xi，μi)，計算

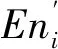
得到中間等級云的數字特征(Ex0，En0，He0)后，通過云變換即可得到邊云的數字特征，由于各指標的分布規律符合正態分布，按正態分布的概率密度函數可得概率分布主要集中在[Ex-3En，Ex+3En]之間，故具體如公式(2)所示。

Ex±1=Ex0+1.5En0

Ex±2=Ex±1+1.5En0

En±1=En±2=En0

He±1=He±2=He0(2)

式中，(Ex+2，En+2，He+2)、(Ex+1，En+1，He+1)、(Ex0，En0，He0)、(Ex-1，En-1，He-1)和(Ex-2，En-2，He-2)分別代表Ⅰ～Ⅴ等級云數字特征。

2 指標體系的功能與建立原則

2.1 指標體系功能

圍巖穩定性評價是一個復雜的非線性動態系統，受物理力學參數和外在水文地質條件、施工狀況等多種因素綜合作用。在前期通常選用單軸抗壓強度、巖體完整性系數、RQD、地下水發育情況和節理狀況5項指標作為分級體系[8-10]，而后逐漸考慮工程因素如相鄰工程影響系數和施工特點等指標對巖體穩定性的影響[19-22]。將各因素分為圍巖巖體、地質因素和工程因素兩大類，圍巖巖體、地質因素反映了地下工程圍巖的力學參數、水文特征和地質特征對穩定性的影響，圍巖工程因素反映了地下工程的施工影響、設計參數和相鄰工程的建設對穩定性的影響。圍巖穩定性是指圍巖巖體、地質因素與工程因素耦合作用下的影響，指標體系的功能如下。

(1)信息功能：圍巖穩定性指標是反映和描述任意時點或時期內圍巖的巖體、地質和工程因素的穩定性情況，進而綜合確定圍巖的穩定性。

(2)監測功能：圍巖穩定性指標是反映和描述某段圍巖的穩定性，進而為支護與設計提供依據，揭示和監測圍巖穩定性與支護之間的規律。

(3)預測功能：通過該段圍巖的穩定性確定下一段圍巖的穩定性，為下一階段的設計和支護提供依據。

2.2 構建評價指標的原則

評價指標是通過少量關鍵指標來反映系統整體性的特點，因此建立評價指標體系必須服從以下原則，使之既具有普遍的適用性，又能體現對圍巖穩定性的指導作用。

(1)全面性：納入體系的指標在總體上應具備一定的系統性和完整性，涉及到圍巖穩定性的各個方面。

(2)科學性：即采用少量指標替代整體的概念，其各指標不具有關聯性，且各指標簡明、清楚和易于量化。

(3)動態性：圍巖的穩定性會隨時間而變化，這就決定了指標體系應具有動態性，即動態地反映圍巖穩定性等級和動態趨勢。

3 指標體系建立

圍巖穩定性的評價指標體系包括指標的選擇、指標體系驗證和指標等級閾值的確定。

3.1 指標體系選擇

指標的選擇是確定指標體系的基礎，本文采用關聯規則挖掘中FP-tree法對各類指標體系進行挖掘得到評價指標，其篩選的過程如下。

3.1.1 建立指標數據庫

指標數據庫的建立是篩選的關鍵，對此本文選用國內外最常用的圍巖分級標準如巖石結構評價(1972)、工程巖體分類(1974)和工程巖體分級標準(2014)等共13個分級標準和知網上關于圍巖穩定性的論文中選取的指標進行匯總，得到圍巖穩定性指標的數據庫。通過最小支持度為0.3，篩選出10項指標作為頻繁項集，分別為A單軸抗壓強度、B巖體完整性系數、C地下水、D節理狀況、E結構面與洞軸組合關系、F結構面狀態、G RQD、H施工影響、I參數設計和J相鄰工程影響。根據篩選后的指標重新建立數據庫，其部分如表1所示。

表1 部分代表性巖體分級標準與文獻

3.1.2 建立FP-tree

依次掃描新數據庫，建立FP-tree，并結合索引表進行關聯挖掘最終確定頻繁項，其FP-tree如圖2所示。

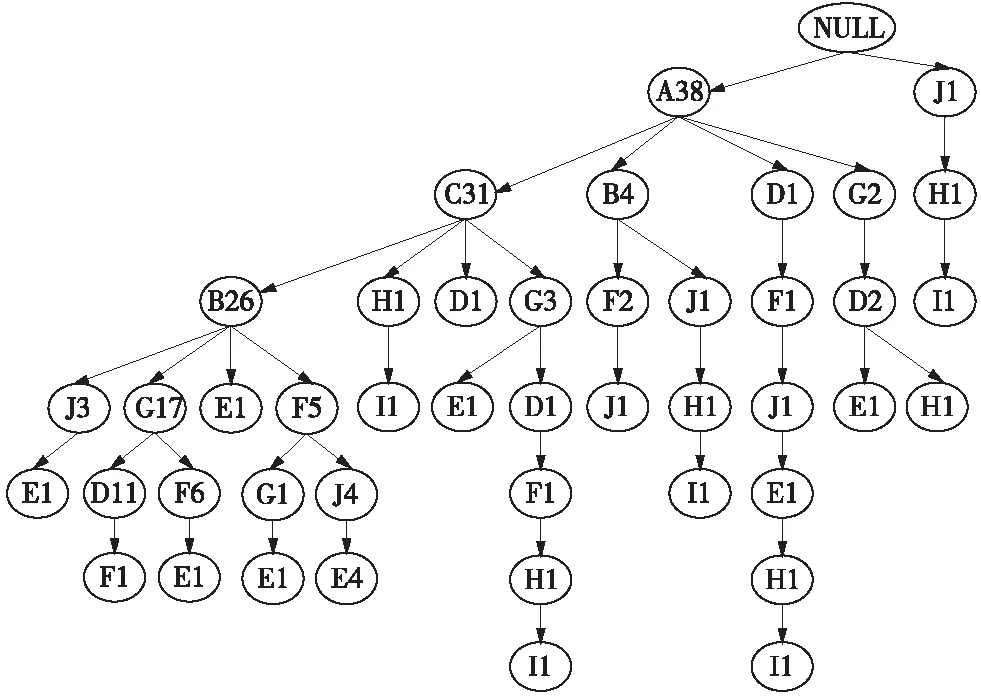
圖2 圍巖穩定性指標FP-tree圖

3.1.3 挖掘最大頻繁項集

FP-tree中每一個分枝均為頻繁集項，通過“自下而上”的方式進行挖掘得到最大頻繁集項即圍巖穩定性的評價指標。由圖2的FP-tree可以確定A分枝最大頻繁集項為(A C B G D)，另一個分枝只有一個分枝(J H I)。其中(A C B G D)的頻數最高，說明這些指標組合選用的次數最多，即通常采用的5項指標，而(J H I)的頻數較少，主要由于這些指標為工程因素，考慮施工和相鄰影響等因素，符合現代分級特點。最終確定圍巖穩定性指標為(A C B G D J H I)，具體指標如表2所示。

3.2 指標體系的驗證

指標體系驗證是確保指標體系有效且適用于圍巖穩定性分級。對此通常采用統計學相關知識對體系進行驗證，包括指標的全面性和相關性及指標的可靠性檢驗。

本文采用大量樣本建立數據庫，通過關聯規則進行挖掘得到評價指標，其全面性和關聯性是滿足的，只需檢驗指標的可靠性即可。指標的可靠性檢驗最常用的方法為變異系數法，可直觀的表達各指標的分布情況，運用SPSS16.0統計軟件計算了初步選擇的8個評價指標的變異系數，各指標的變異系數如表3所示。由表3可知，各指標的變異系數分布沒有過于集中也不是過于分散，且各指標變異系數的大小與各指標的重要性排序基本吻合，故驗證了指標的穩定性。

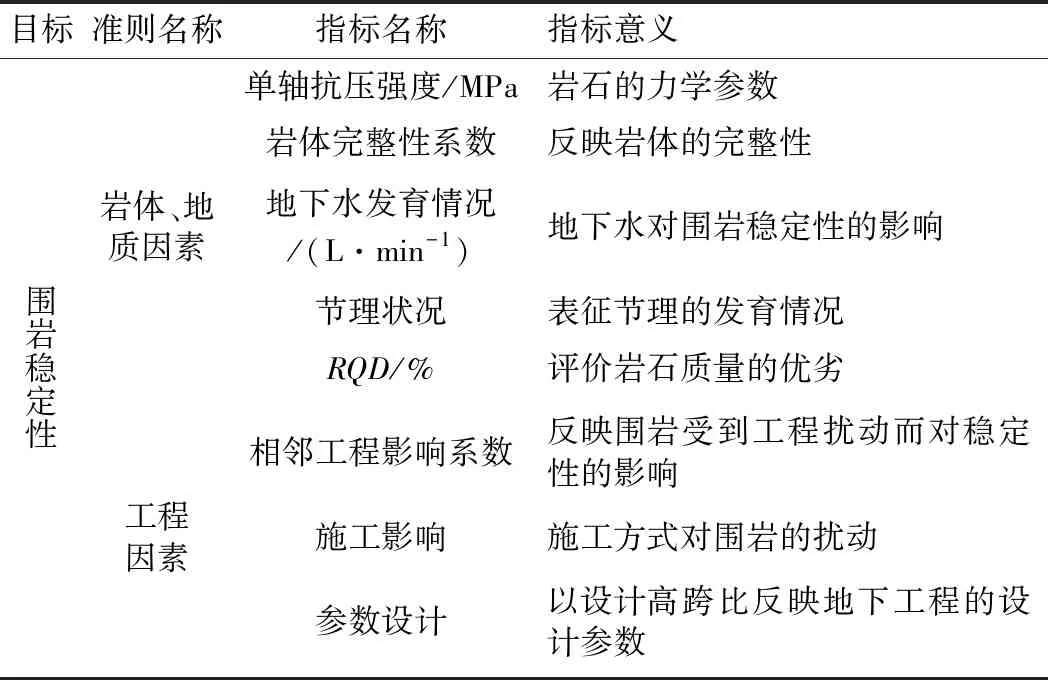
表2 圍巖穩定性指標

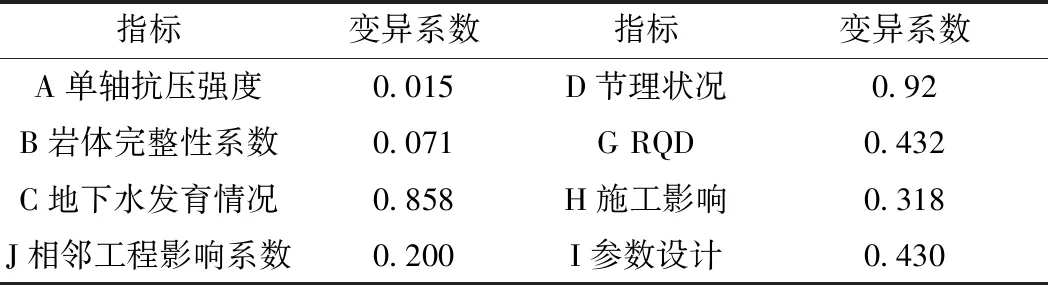
表3 各指標變異系數

3.3 指標等級閾值的確定

傳統指標體系中指標的等級閾值為經驗總結的結果，為某一確定的數值，難以兼顧等級的模糊性。對此本文采用云變換理論，通過逆向云發生器對大量指標數據進行分析，再通過云變換得到不同等級的云圖，實現了等級的“軟劃分”，其各指標等級云圖如圖3所示。

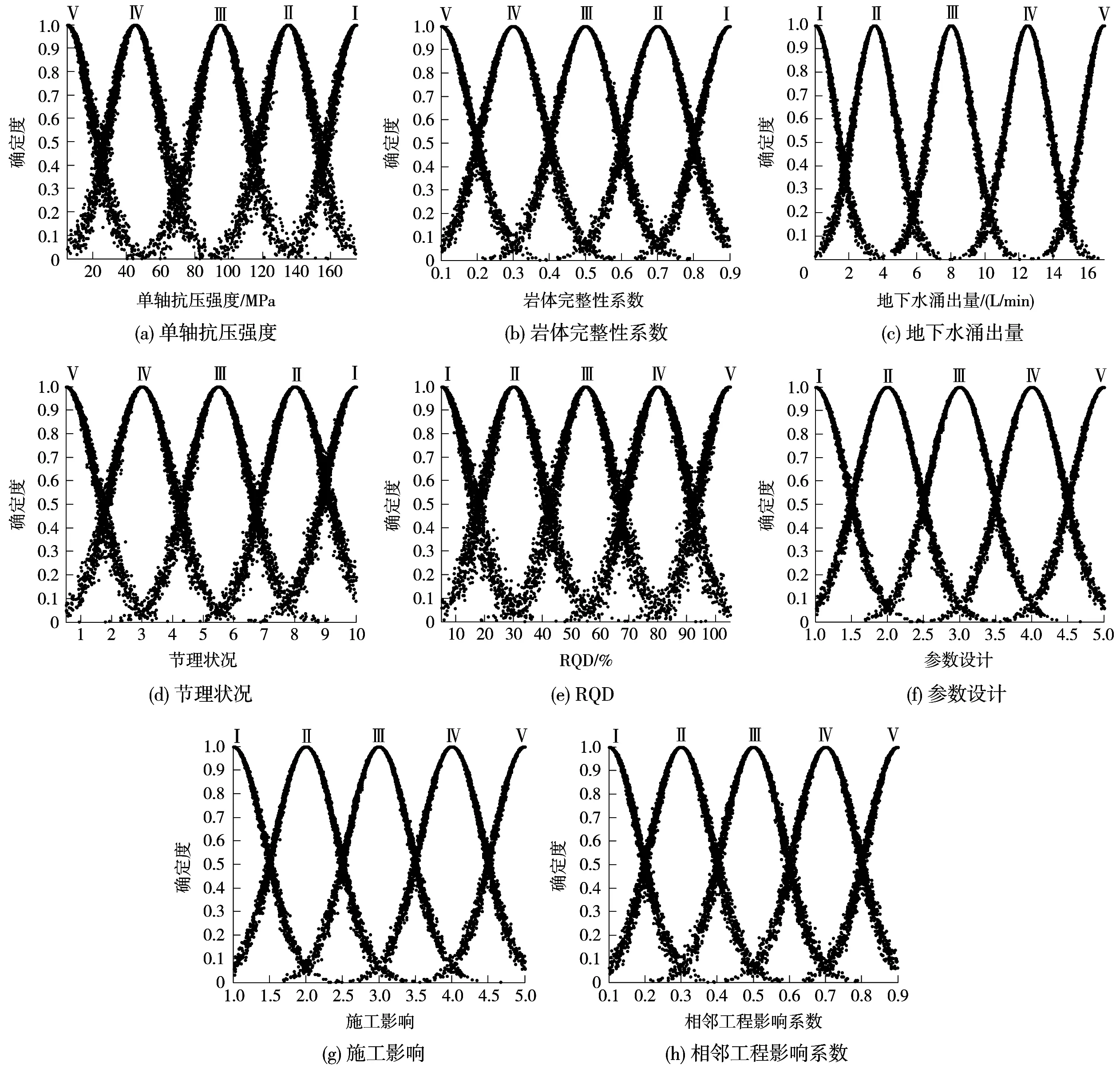
圖3 各指標的等級云圖

由圖3可得指標等級為一個云圖，而不是取值范圍，且各云圖存在交叉，可以兼顧等級閾值的模糊性。同時也可以對定性指標進行量化。圍巖穩定性的云圖既可以確定各指標的等級，也構造了確定度函數，為模糊綜合評價和未確知測度等理論提供了基礎。該云圖上某一點的確定度不是一個固定值，而是在一定范圍內隨機波動的，體現了系統的隨機性，通過云變換得到的指標閾值可以兼顧模糊性和隨機性。

4 實例驗證

為了驗證該體系的準確性，將該體系運用在工程實例中，本文采用文獻[22]中礦區工程G450為例進行驗證。已知該礦區地質條件復雜，水文發育程度極不均勻，巷道情況復雜，且相鄰工程影響較大。該礦區的工程G450中包含3個斷面，分別是D1、D2和D3，其中斷面D1和D3的巖體強度相差不大，而D2巖體強度較小；D1和D3的地下水較發育；D2受相鄰工程影響較大；3個斷面的高跨比相差比較大，其中具體各指標數據參考文獻[22]，如表4所示。

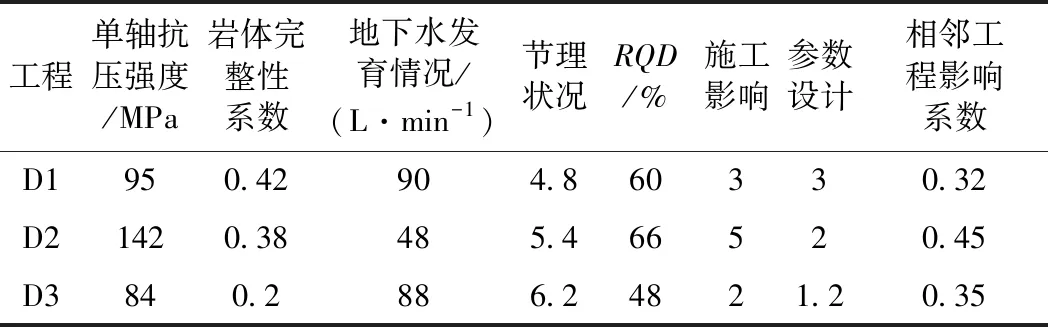
表4 樣本實測值

本文采用層次分析法確定各指標權重矩陣W(0.091 2，0.123，0.095 4，0.099，0.191 4，0.066 8，0.200 4，0.132 8)。將工程G450中各指標數據帶入指標云圖中，通過云發生器確定各指標的確定度矩陣U。將權重矩陣與確定度矩陣結合，得到評價矩陣R(R=W·U)。最后通過最大確定度原則確定等級，并將得到的結果與模糊綜合評價(FU)，未確知測度理論(UM)和工程實際情況進行對比，其結果如表5所示。

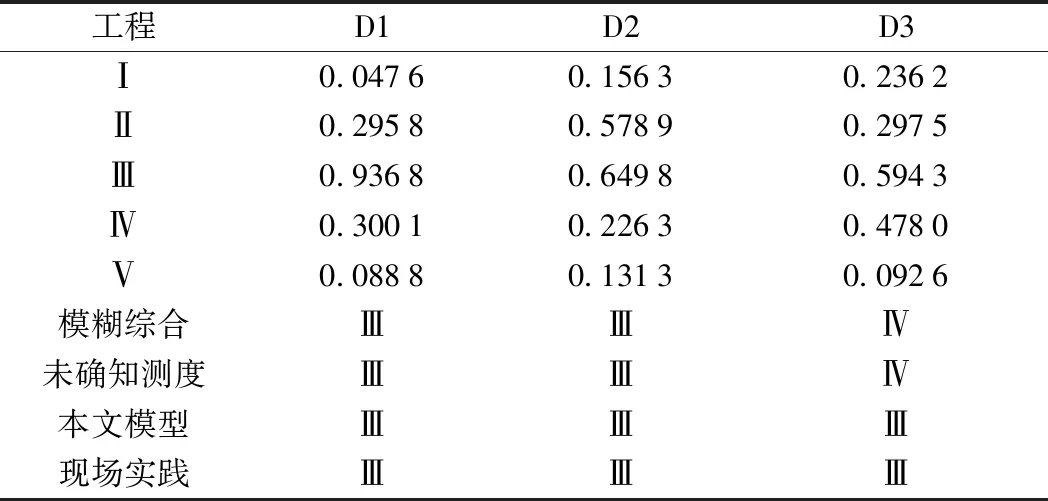
表5 圍巖穩定性評價結果及其對比

通過表5可以得出，本文模型對工程D1和D2的評價結果與其他方法完全一致，D3工程與未確知測度理論和模糊綜合評價的等級不一致。經調研和資料分析得到工程D3巖體破碎，地下水發育中等，高跨比較小，符合圍巖穩定性Ⅲ級的特征，且工程D1到D3的距離不大，工程地質條件相似，巖體內部不存在大斷層破壞的現象，難以判定工程D3為Ⅳ級。現場對工程G450的評價為Ⅲ級，與本文模型得到的結果相同，驗證了本文模型的合理性。本文考慮了工程因素對圍巖穩定性影響，建立了定向與定量相結合的指標體系。選取的指標較合理。

5 結論

圍巖穩定性的科學評價一直是研究的重點問題，其中，如何在眾多指標中篩選指標和建立科學的分級標準是科學評價的核心。

(1)本文將穩定性指標進行匯總，采用FP-tree法通過關聯挖掘得到圍巖穩定性的指標，并對各指標的全面性、關聯性和穩定性進行驗證。采用云變換確定各指標等級的閾值，實現等級的“軟劃分”，考慮評價等級閾值的模糊性，最終建立圍巖穩定性分級體系。

(2)將該體系運用在工程實例中，驗證了該體系的適用性與合理性。為圍巖穩定性提供一套簡潔方便的評價體系，為其他的評價體系構建提供了一套科學、合理的方法。