基于測錄波形的鐵芯設備勵磁特性轉換方法探討

李特　周國良　金涌濤　王少華　于淼

摘要：為獲得鐵芯設備伏安特性向勵磁特性的簡便轉換方法，該文從勵磁特性定義出發，給出基于電流有效值、電壓平均值的處理方法和基于電流峰值、電壓平均值的處理方法，并針對其處理方法在鐵芯飽和下的適用性、電流有效值法帶來的誤差進行分析。結果表明：隨鐵芯飽和程度加深，電流諧波含量增加，電流有效值法造成的誤差增大。利用對放電線圈放電過程的仿真計算與試驗測量，并對比不同方法所測勵磁曲線用于計算結果，結果表明利用電流峰值法所得勵磁特性比電流有效值法結果更適用于鐵芯設備電磁暫態的計算分析。

關鍵詞：勵磁特性;電流峰值;電流有效值;諧波

中圖分類號：TM85

文獻標志碼：A

文章編號：1674–5124（2019）02–0054–05

0 引言

勵磁特性測量對于含鐵芯設備（變壓器、電磁式電壓互感器（PT）、電流互感器（CT）、放電線圈等）有著重要意義。通過測得的勵磁特性與歷史數據的對比可以檢查PT、CT、放電線圈等設備是否存在匝間短路[1]，對于保護用CT，勵磁特性是求取10%誤差曲線的基礎，因此標準將勵磁特性測量列為PT的型式試驗和例行試驗項目，并規定交接時要對CT保護用繞組進行勵磁特性測量。同時在對含非線性鐵芯電感的設備進行鐵磁諧振分析、涌流計算等故障分析和理論計算時，先要取得其勵磁特性[2-4]。

目前應用較多的勵磁特性測量方法包括工頻交流法、低頻法、直流法等，與設備運行工況具備等效性、工程應用最廣泛的方法是工頻交流法，本文主要對該方法進行討論。目前使用的互感器、放電線圈試驗標準大多未對測量用電流表的類型做出規定[5-7]，而在設計互感器綜合特性分析儀時，存在使用電流有效值進行勵磁特性數據處理的情況[8-9]。然而隨著勵磁電流增大，鐵芯飽和后電流波形發生畸變，使用電流有效值將給勵磁特性的求取帶來較大誤差，然而相應誤差的定量分析極少見于報道。使用伏安特性向勵磁特性轉換時，常用方法有給定勵磁特性函數并求取函數參數的試探法、Gauss-Newton法[10-12]，但其計算過程較為繁瑣。

本文在總結現有測量方法基礎上，從勵磁特性定義出發，給出勵磁特性的簡便轉換方法，包括未發生飽和時使用電流有效值、電壓平均值的勵磁特性曲線轉換方法，以及適用于飽和情況下基于電流峰值和電壓平均值的勵磁特性處理方法，并對使用電流有效值帶來的誤差進行了分析。以放電線圈為例，使用本文所提方法測量其勵磁特性，利用測量結果在EMTP中對單相電容器-放電線圈回路的飽和放電波形進行了仿真，并與實測放電波形比較，驗證了使用電流峰值進行磁化曲線測量的準確性。

1 測試原理

1.1”電流有效值法

電壓平均值、電流有效值的方法簡稱為電流有效值法，其通常在被試繞組兩端施加電壓，以勵磁電流讀數為準，讀取電壓值，當對某一組繞組進行試驗時，其他繞組均處于開路狀態。試驗電路如圖1所示，TV為調壓器，V為平均值電壓表，A為電流表，T為被試繞組。

交流電路中鐵芯的勵磁特性是一系列磁滯回線的頂點，由電流峰值imax與磁鏈峰值φmax決定。對于正弦交流電路，鐵芯繞組兩端電壓u（t）與鐵芯磁通φ（t）的關系為

其中N為鐵芯繞組匝數，ω0為回路角頻率。

由式（1）可知繞組兩端電壓有效值Urms、電壓峰值Umax、磁通峰值φmax三者成正比，同時電流有效值irms與電流峰值imax成固定比例關系，因此伏安特性（irms～Urms）與磁化曲線（imax～φmax）形狀相同，此時可以通過測得的伏安特性進行線性變換得到磁化曲線，如下式所示：

其中Uave為電壓波形在正半周或負半周的絕對值平均值。

當u（t）、i（t）均為正弦波時，理想條件下忽略鐵芯繞組電阻，φ（t）與u（t）相位相差90°，因此φmax出現于u（t）=0的時刻，此時令t=t1，在t1之前1/4個周期的時刻t0，φ=0。因此有：

50Hz交流系統中式（4）與式（3）等價。通過上述過程取得的只是磁化曲線上的離散點，通過插值或函數擬合，進而可以得到完整的勵磁特性。

1.2 電流峰值法

電壓平均值、電流峰值的方法簡稱為電流峰值法，實際是對1.1節電流有效值法的改進，利用錄波儀記錄勵磁電壓和勵磁電流實時波形，對波形進行數學處理得到基本勵磁曲線所需的電流、磁通值。測量接線如圖2所示，K為電流鉗，DL750為橫河750錄波儀，在鐵芯設備的二次繞組進行測量，電壓、電流信號利用橫河750錄波儀進行記錄，電壓信號利用錄波儀探頭直接從繞組端頭獲取，電流信號利用福祿克電流探頭從調壓器輸出端獲取。

得到勵磁特性imax～φmax的關鍵就在于imax、φmax的求取。在若干勵磁電壓下進行測量，鐵芯線圈逐漸飽和的過程中，繞組電流所含的諧波以奇次諧波為主[11]，每次測量的電流峰值可通過電流諧波分析得到，其表達式可寫為

將i（t）在時間軸上平移后再進行傅里葉變換，可使式（5）中所有諧波的初相角為0，因此繞組電流峰值為

實際計算時k=11[11]。磁鏈φ與電壓的關系為

考慮到鐵心飽和時其電壓所含諧波主要為奇次諧波[11]，u（t）波形每個周期中正負半周對稱、各正負半周中又左右對稱，此時φmax仍然出現于u（t）=0的時刻，此時令t=t1，在t1之前1/4個周期的時刻t0，φ仍然為0因此式（3）仍然成立，即φmax仍然由式（3）求取。基于采集到的電壓波形，根據式（3）只需進行簡單的平均值處理即可得到φmax，而不需如文獻[10-12]中復雜的計算處理。

1.3 電流有效值法誤差分析

當鐵芯發生飽和，勵磁電流發生畸變，此時式（2）不再成立，電流有效值法將產生測量誤差。

由1.2節已知在電流因飽和而畸變時，繞組電流峰值如式（6），而有效值I為

利用有效值反推峰值造成的電流峰值相對誤差Err為

由電流畸變引起的誤差，電流互感器和放電線圈的各項標準上并沒有給出畸變后的校正方法。對于電壓互感器，標準GB/T22071.2—2008《互感器試驗導則第2部分：電磁式電壓互感器》[6]規定，當平均值電壓表與有效值電壓表讀數相差在2%以上時，則需要分別以平均值電壓表和有效值電壓表為準施加到規定值讀取電流值，然后取兩次測量電流值的平均值作為測量值，以此對電流進行校正。這一方法并沒有涉及到電流波形畸變后電流峰值與電流有效值關系變化這一實質，校正后偏差仍然存在。因此，電流因飽和而畸變后測量不夠準確始終是電流有效值法的缺點。

2 測試與分析

2.1 測量試品

本文以放電線圈為例，利用測量回路圖2獲取其勵磁電壓、勵磁電流波形，并分別使用電流有效值法、電流峰值法進行勵磁特性的轉換，測量所用放電線圈參數列于表1。

標準JB/T8970—2014《高壓并聯電容器用放電線圈》[7]規定了放電線圈勵磁特性測量點為0.2，0.5，0.8，1.0，1.1，1.3，1.5倍額定電壓，本文在上述電壓范圍內適當增加了測量電壓點數。

2.2 測量結果對比及誤差分析

對采集得到的放電線圈電流波形i（t）首先進行諧波分析，利用諧波峰值根據式（6）、式（8）、式（9）可分別得到電流峰值、有效值、由有效值反推峰值帶來的誤差，分別由字母imaxh、Ih、Errh表示，即為通過諧波分析得到的電流有效值法測量誤差。

同時，利用Matlab對波形進行處理，直接搜索電流波形得到電流峰值。在實驗室中進行測量外界干擾極小，利用直接搜索得到的電流峰值即為電流波形的真實峰值，從定義出發利用直接積分程序從電流波形得到電流有效值，進而利用式（9）由有效值反推峰值帶來的誤差，分別由imaxm、Im、Errm表示，上述3個量由從定義出發對電流波形進行處理得到，可確保相應值的正確性。此外，計算電流的諧波含量kh為

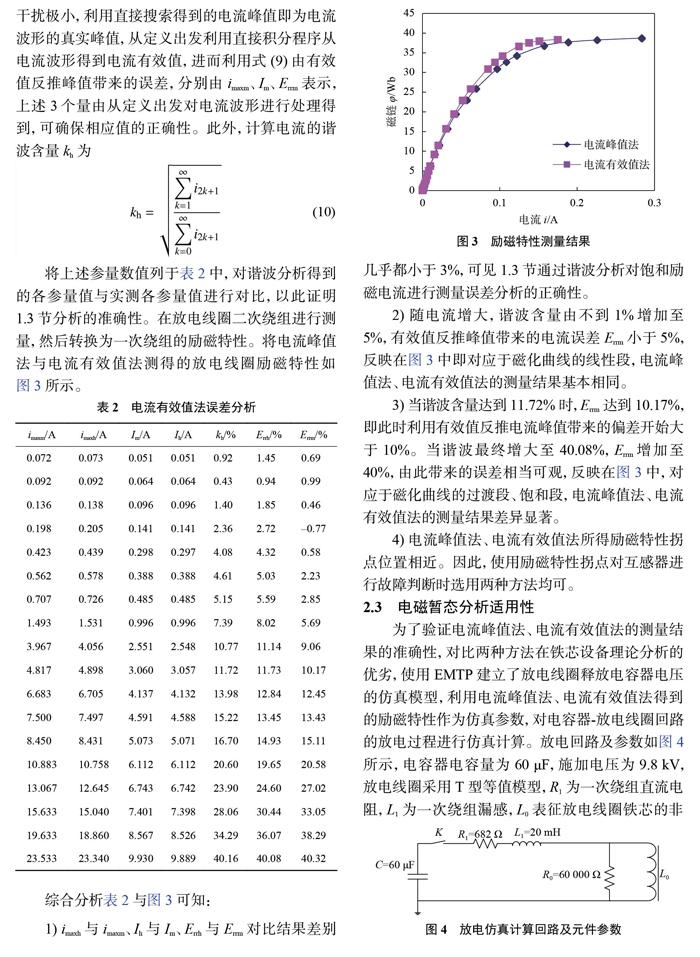
將上述參量數值列于表2中，對諧波分析得到的各參量值與實測各參量值進行對比，以此證明1.3節分析的準確性。在放電線圈二次繞組進行測量，然后轉換為一次繞組的勵磁特性。將電流峰值法與電流有效值法測得的放電線圈勵磁特性如圖3所示。

綜合分析表2與圖3可知：

幾乎都小于3%，可見1.3節通過諧波分析對飽和勵磁電流進行測量誤差分析的正確性。

2）隨電流增大，諧波含量由不到1%增加至5%，有效值反推峰值帶來的電流誤差Errm小于5%，反映在圖3中即對應于磁化曲線的線性段，電流峰值法、電流有效值法的測量結果基本相同。

3）當諧波含量達到11.72%時，Errm達到10.17%，即此時利用有效值反推電流峰值帶來的偏差開始大于10%。當諧波最終增大至40.08%，Errm增加至40%，由此帶來的誤差相當可觀，反映在圖3中，對應于磁化曲線的過渡段、飽和段，電流峰值法、電流有效值法的測量結果差異顯著。

4）電流峰值法、電流有效值法所得勵磁特性拐點位置相近。因此，使用勵磁特性拐點對互感器進行故障判斷時選用兩種方法均可。

2.3 電磁暫態分析適用性

為了驗證電流峰值法、電流有效值法的測量結果的準確性，對比兩種方法在鐵芯設備理論分析的優劣，使用EMTP建立了放電線圈釋放電容器電壓的仿真模型，利用電流峰值法、電流有效值法得到的勵磁特性作為仿真參數，對電容器-放電線圈回路的放電過程進行仿真計算。放電回路及參數如圖4所示，電容器電容量為60μF，施加電壓為9.8kV，放電線圈采用T型等值模型，R1為一次繞組直流電阻，L1為一次繞組漏感，L0表征放電線圈鐵芯的非線性電感特性，R0表征放電線圈鐵芯的損耗特性，根據實際損耗情況確定電阻值。

同時搭建試驗回路，對相應參數試品電荷釋放過程中的電容兩端電壓電流進行實測。

在仿真計算中，非線性電感L0需要設置磁化曲線，分別代入圖3中電流峰值法、電流有效值法方法得到的勵磁特性，計算得到不同勵磁特性對應的電容器-放電線圈放電過程計算結果，如圖5所示。

圖5中，計算波形1為利用電流峰值法所測勵磁特性計算得到的結果，計算波形2為利用電流有效值法所測結果計算得到的結果。由圖可知，與波形2相比，波形1更接近實測結果，波形1與實測波形基本重合;而波形2位于實測波形下方，與實際波形的偏差更大。因此，利用電流峰值法得到的勵磁特性用于單相電容器-放電線圈回路的放電過程計算時，計算結果優于電流有效值法所得勵磁特性對應的結果，即電流峰值法測量得到的磁化曲線更為準確，更適用于針對鐵芯設備的電磁暫態過程理論計算。

3 結束語

本文給出了基于電流有效值與電流峰值的勵磁特性簡化轉換方法，并通過實測與仿真計算分析了飽和情況下電流有效值法的誤差，及電流峰值法對電磁暫態分析的適用性，結果表明：

1）交流法測量勵磁特性時，使用電流有效值法會帶來誤差，且隨鐵芯飽和程度的增加而增大;勵磁特性過渡段與飽和段的電流數值偏低。

2）使用電流有效值法和電流峰值法所得勵磁特性拐點位置相近，以勵磁特性拐點為根據對互感器進行故障判斷時兩種方法效果一致。

3）對鐵芯設備電磁暫態分析時，建議使用電流峰值法適應性較好。

參考文獻

[1]劉影，謝馳.直流偏磁下變壓器的鐵心損耗分析研究[J].中國測試，2017，43（7）：124-127.

[2]蘭華，王彬，楊亮，等.PT勵磁特性對鐵磁諧振的影響及檢測研究[J].電測與儀表，2010，47（10）：10-14.

[3]牛福生，王學濤，白麗梅，等.新型比磁化系數測定儀的研制及其數值模擬研究[J].中國測試，2017，43（6）：60-64.

[4]王俊凱，梁仕斌，劉濤，等.鐵磁元件勵磁特性低頻測量方法[J].電工技術學報，2017，32（10）：168-173.

[5]電壓互感器試驗導則：JB/T5357-2002[S].北京：中國計量出版社，2002.

[6]互感器試驗導則第1部分：電流互感器：GB/T22071.1-2008[S].北京：中國計量出版社，2008.

[7]高壓并聯電容器用放電線圈：JB/T8970-2014[S].北京：中國質檢出版社，2014.

[8]李銘軒.基于ARM的發電機互感器伏安特性測試系統的設計與實現[D].北京：北京交通大學，2007.

[9]丁心志，梁仕斌，劉濤，等.基于雙單片機的新型電流互感器綜合特性測試儀的研制[J].電測與儀表，2010，47（6）：69-72.

[10]李謙，陳猷清，王曉瑜，等.變壓器和電磁式電壓互感器鐵心勵磁特性轉換方法的探討[J].變壓器，1993，12：10-13.

[11]蔣金，周鶚.利用正弦交流電源測量基本磁化曲線的方法[J].微特電機，1989（5）：1-5.

[12]李遠松，高博，丁津津，等.特高壓保護用電流互感器勵磁特性現場測試[J].變壓器，2016，53（7）：73-76.