含逆變型分布式電源的配電網正序和商阻抗縱聯保護
雷 霖,唐成達,張 鵬,趙永鑫,賴真良
(1.西華大學電氣與電子信息學院, 四川 成都 610039;2.成都大學信息科學與工程學院, 四川 成都 610106)
隨著新能源的日益發展,電力工業出現了由傳統大規模集中式供電模式向集中式與分布式相結合的過渡。電力系統中DG滲透率的升高,使傳統的配電網保護方案面臨嚴峻考驗[1]。目前,關于含DG的配電網保護研究[2-8]較多。文獻[2-3]通過限制DG的準入容量,利用故障后電流幅值的差異,構造了新型縱聯保護方案。這類保護方案都是以系統穩定狀態為前提,并未考慮系統故障等特殊狀態,因此得到的準入容量偏于樂觀。文獻[4-5]分別根據配電網樹狀結構和DG“T”接線結構特征,提出了自適應保護原理及實現方案。自適應保護方案需要實時檢測配電網結構,不能應用于多DG接入的配電網。文獻[6-8]構造了故障區段定位的數學模型,并采用和聲算法、遺傳算法對其進行求解,從數學角度解決故障定位問題。這類保護方案需要處理大量的數據,對主站要求高,并且需要實時上傳大量數據,對通信的要求高。
為防止DG大規模脫網事故的發生,現階段并網標準對分布式電源的低電壓穿越能力提出了要求,使含DG的配電網保護更加復雜[9]。由于IIDG在系統故障時可等效為僅存在于正序網絡中的壓控電流源[10],文獻[10-12]提出了基于正序故障分量的保護原理。文獻[10]借鑒電流差動保護標積制動特性,提出了帶制動特性的正序阻抗縱聯保護方案。文獻[11]利用母線正序電壓故障分量與各饋線正序電流故障分量的相位特征實現故障定位。文獻[12]設計了由相量測量單元和數字繼電器構成的數字通信系統,提出了一種基于正序分量的保護策略。然而,IIDG的故障特性較為復雜,上述保護方案可靠性仍有待研究。
本文分析了線路區內與區外故障時,線路兩端正序電壓相量之和與正序相量電流之和的比值特點,提出了一種基于故障正序分量和商阻抗的縱聯保護新原理,并使用PSCAD/EMTDC建立仿真模型對新原理進行了驗證。
1 正序和商阻抗保護算法的原理
1.1 正序和商阻抗的概念
圖1為含IIDG的簡單配電網示意圖。本文涉及的分布式電源都采用低電壓穿越特性的控制策略,具體控制方式文獻[11]詳細給出,此處不再贅述。
定義線路兩端正序電壓之和與線路兩端正序電流之和的比值為正序和商阻抗。
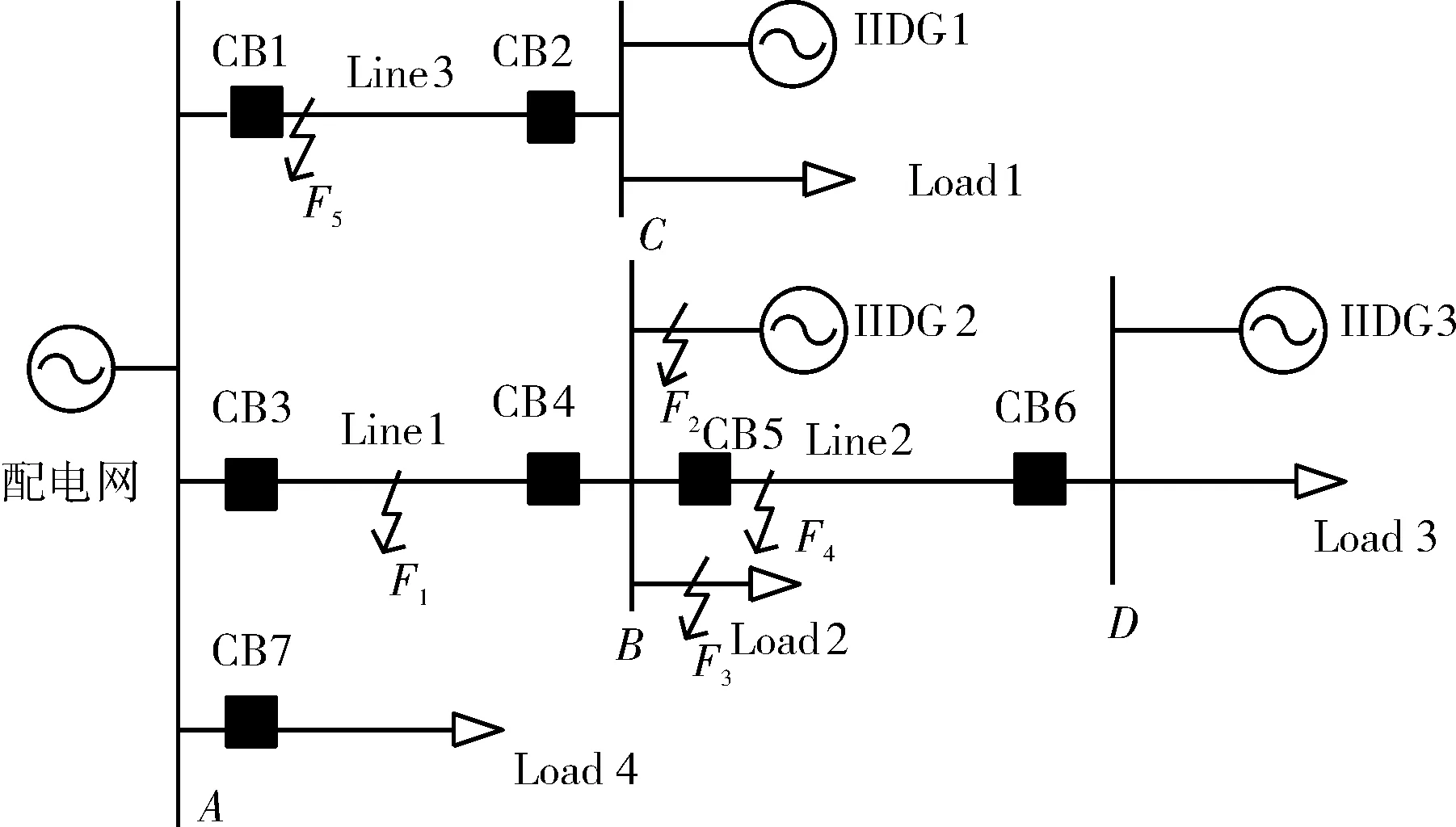
圖 1 含IIDG的配電網示意圖
(1)
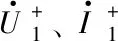


圖 2 區外F4故障正序分量網絡
此時有
(2)
區外故障正序和商阻抗為
Zcd=ZC
(3)
即線路發生區外故障時,Zcd為線路容抗值,相對于系統和線路的正序阻抗,其值較大。
2)區內故障。35 kV及以下配電網大多采用中性點不接地的方式運行,當系統發生相間故障時,中性點不接地系統與中性點接地系統相間短路的正序網絡圖相同;當系統發生相間接地故障時,電源與故障點之間無法形成回路,此時中性點不接地系統與中性點接地系統相間接地故障的正序網絡圖將不同:因此,有必要將相間故障與相間接地故障分開討論。
①區內發生相間故障時,正序故障分量中包含的電容電流可以忽略。圖3為線路Line1發生區內兩相短路時的正序網絡圖。

圖 3 區內相間故障正序分量網絡
根據圖3可得饋線正序電壓分別為:
(4)
(5)
(6)
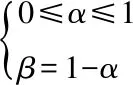
則|Zcd|滿足
|Zcd|≤|ZL1+2Rf|<|ZL1|+2Rf
(7)
即線路發生區內相間故障時|Zcd|max=|ZL1|+2Rf。
②區內發生兩相接地故障時,文獻[13]利用對稱分量法詳細推導了中性點不接地系統BC相經過渡電阻接地時A相序分量關系:
(8)
式中:Ua1、Ua2、Ua0分別為A相的正序、負序和零序電壓;X2∑為A相負序阻抗;Ia1為A相正序電流。輸電線路的正序阻抗與負序阻抗相等,可知中性點不接地系統的正序網絡中除故障支路電阻將變為原來的2倍以外,其他參數不變。
可知,區內發生相間接地故障時的正序網絡圖與圖3相似,只是將過渡電阻支路由Rf替換為2Rf。用2Rf依次替換式(4)(5)(6)(7)中的Rf,此時|Zcd|滿足
|Zcd|≤|ZL1+4Rf|<|ZL1|+4Rf
(9)
即線路發生區內相間接地故障時
|Zcd|max=|ZL1|+4Rf
(10)
參照文獻[14-15],10 kV電壓等級線路供電半徑和線路對地電容電流有表1的特點。
1.2 基于正序和商阻抗的縱聯保護判據
通過以上分析可知,當線路區內無故障時理論上測量得到的|Zcd|值為對地容抗值,|Zcd|在10 kV
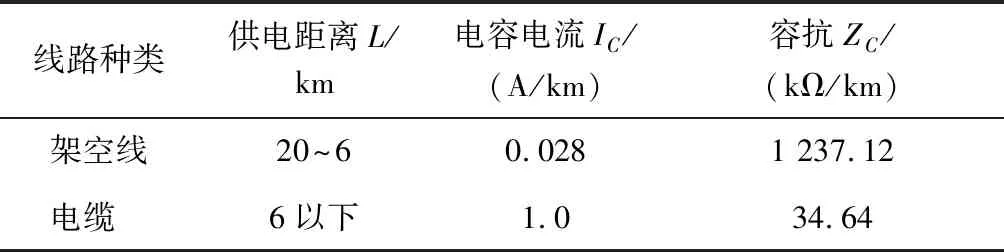
表1 不同線路類型的10 kV線路特點
供電范圍內為一個kΩ級別的數值,具體數值由輸電線路的電壓等級、線路長度和線路種類確定。當線路發生區內故障時,相同過渡電阻條件下,將在線路發生相間接地故障時得到|Zcd|最大值,為|ZL1|+4Rf。中低壓配電網相間故障Rf取值一般為1~2Ω,發生接地故障時Rf的取值可以從0到幾百Ω[16];因此,可以根據|Zcd|的大小來區分是線路區內故障還是區外故障。據此提出基于正序和商阻抗的縱聯保護原理,判據為
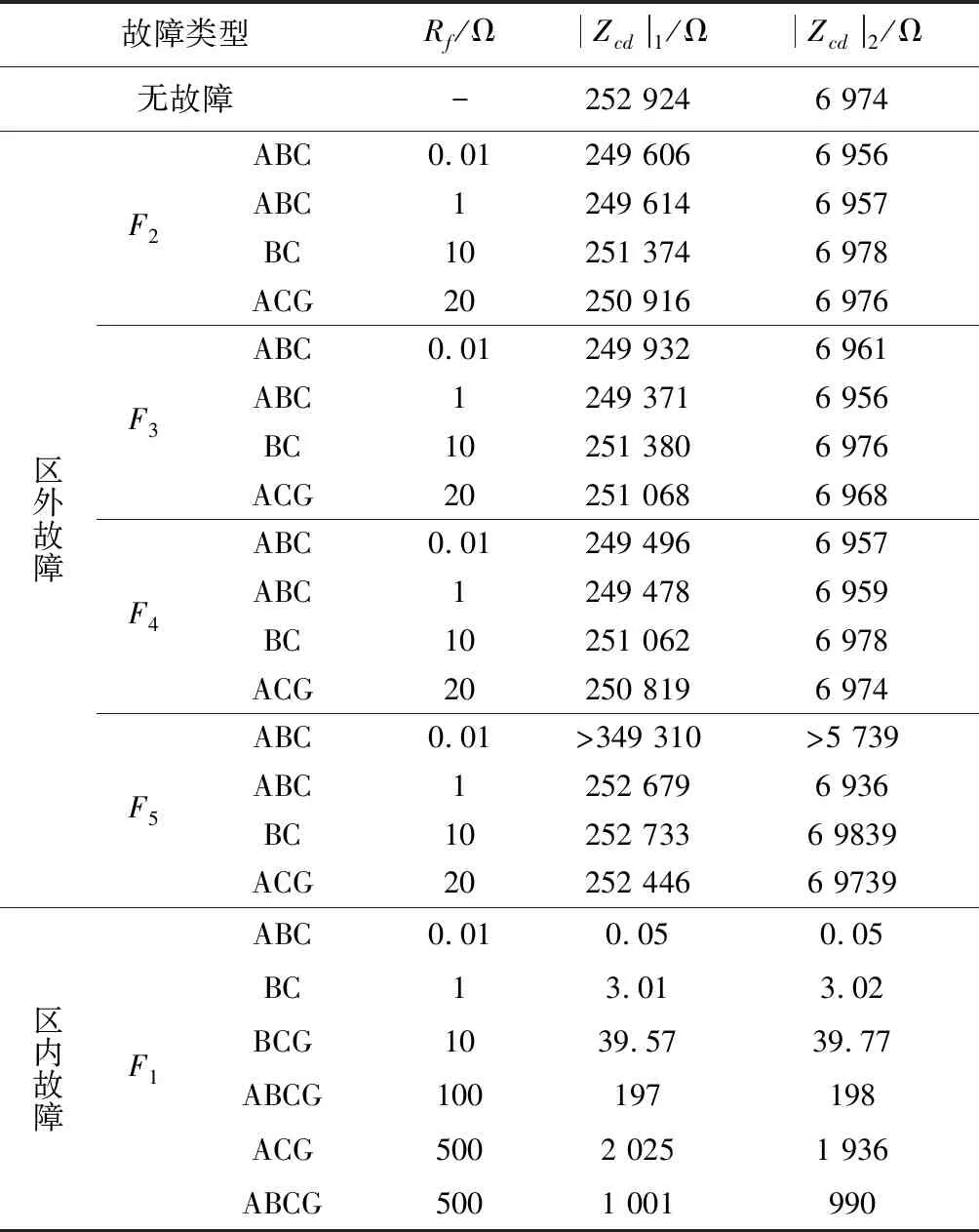
|Zcd| (11) 式中Zset為阻抗定值。整定原則為 Zset=kZC (12) 式中k為可靠系數,從第3節仿真結果可知k一般可取0.5~0.6,能夠保證區外故障不誤動。 以電壓等級為10 kV、長度為5 km的電纜線路為例,ZC的值約為6.93 kΩ,可以將Zset整定為3.47~4.16 kΩ。當線路長度變短時,ZC值將變大,由式(12)整定的Zset也將變大,為便于整定,此時可將Zset直接取為3.47 kΩ。 基于正序和商阻抗縱聯保護的輸電線路,其動作值只與線路對地容抗值ZC有關。在實際的配電網當中,線路種類和長度一旦確定,ZC值主要受環境因素的影響,相較于故障狀態其值變化不大。低壓配電網線路容抗值遠大于可能出現的過渡電阻值,因此只要式(12)中的可靠系數選取合理,即使線路區內發生大過渡電阻接地故障,也能實現故障的快速識別。 在高壓輸電線路的電流縱聯保護中,當暫態分量超過一定值時必須退出保護,并提高動作門檻,然而電容電流較大暫態分量消失較慢,從而降低了靈敏度。對于中低壓配電網系統,電容電流較小,由第3節大量仿真可知,Line1下游發生故障時,電容電流幾乎不影響|Zcd|的測量值;當故障發生在Line2上游母線出口處時,受IIDG控制策略影響,|Zcd|值將發生震蕩,只要可靠系數選取得當仍能避免保護誤動。當線路發生區內故障時,只有故障電流值與原電壓等級線路對地電容電流值接近,電容電流含有的直流分量才會明顯影響|Zcd|的測量值,此時對應線路發生大過渡電阻故障,直流分量將迅速衰減。因此,線路區內發生大過渡電阻故障而受到暫態分量的影響時,保護仍會快速動作。 當系統發生故障時,IIDG的控制策略將影響其輸出電流與接入點電壓的相位。由于本文涉及的IIDG采用正序分量的控制策略,當線路發生不對稱故障時,其輸出的故障電流只包含正序分量,即IIDG只包含在正序網絡中。線路區內外無故障時,分別采用電壓電流全相量和正序電壓電流相量計算得到的|Zcd|值將相等。線路區外一旦發生故障,電壓電流全相量包含的負序分量將導致計算值|Zcd|產生較大波動,容易導致保護誤動,而采用正序和商阻抗的縱聯保護很好地解決了這一問題。 由于可再生能源的間歇性,難免造成分布式電源的頻繁投切,而分布式電源出力發生改變及投切過程中線路對地電容不會發生改變;因此,對判據(11)中的|Zcd|計算值影響不大,本文提出的正序和商縱聯保護原理在DG出力發生改變及投切過程中仍具有較好的適用性。 線路空載合閘模型如圖4所示,圖4(a)為合閘于無故障的線路模型,圖4(b)為合閘于故障的模型。 圖 4 空載合閘系統模型圖 當線路無故障時,如圖4(a),正序和商阻抗滿足式(3),為 |Zcd|=ZC 當線路存在故障時,如圖4(b),則 式中ZL為線路阻抗。可見:在線路合閘時,若線路無故障,|Zcd|與ZC相等;若線路有故障,|Zcd|反映保護安裝處到故障點的線路阻抗與過渡電阻之和,其值與線路容抗值相差較大。基于此,使用基于正序和商阻抗的縱聯保護判據可以區分線路上是否有故障。 為驗證所提保護原理在復雜配電網中的適應性,采用PSCAD仿真軟件搭建如圖1所示的有源配電網模型。配電網電壓等級為10 kV,容量為10 MVA, IIDG采用低電壓穿越的PQ運行控制策略,IIDG1—IIDG2的額定容量為0.5 MVA。線路采用∏型等效參數模型,線路Line1、Line2長度分別為5、4 km,Load1—Load4為三相負載,視載功率分別為0.9、0.5、1、2 MVA,且功率因數都為0.9。仿真中,分別在F1—F55個點模擬不同故障,整定時k取值為0.5。 仿真模型1:Line1、Line2都為架空線路,單位阻抗和導納分別為0.838+j0.395 Ω/km,1.545×10-8S/km。 仿真模型2:Line1為電纜線路,單位阻抗和導納分別為 0.870+j0.120 Ω/km,5.516×10-7S/km;Line2為架空線路,單位阻抗和導納分別為 0.838+j0.395 Ω/km,1.545×10-8S/km。 設定t=0.3 s時發生故障,此時系統電壓下降將會導致IIDG的出力發生改變,從而對正序和商阻抗的計算產生影響。圖5與圖6表示母線A出口F5處發生三相金屬性短路時,線路Line1為不同線路種類,分別采用電壓電流正序分量和全相量得到的|Zcd|測量值。 從圖5可以看出,當系統發生嚴重故障時,由于IIDG失去了系統電壓的支撐,IIDG將進行低電壓穿越,因此在故障發生一個周期內|Zcd|發生較大的震蕩,隨后測量值超過穩態值并繼續震蕩。圖5(a)和圖5(b)中的最小值分別為349.31 kΩ和5.739 kΩ,都能滿足保護不誤動。 圖6為采用電壓電流全相量計算得到的|Zcd|值。與圖5對比可知:系統無故障時,2種方法計算得到的|Zcd|值相等;區外發生故障時,一個周期內|Zcd|也會發生震蕩,但是采用全向量計算得到|Zcd|的震蕩幅度遠大于采用正序分量計算得到|Zcd|的震蕩幅度,容易導致保護的誤動作。仿真驗證了采用正序分量和商阻抗保護的穩定性。 圖 5 采用正序分量|Zcd|的測量值 圖 6 采用全相量時|Zcd|的測量值 圖7表示在F4點發生三相金屬性短路時,Line1為不同線路種類時|Zcd|的測量值。與圖5所示情況不同,雖然系統電壓也會有所下降,但Line1靠近系統側,受分布式電源出力影響較小,|Zcd|值震蕩較小,因此在較短時間內|Zcd|值接近穩定值。 圖 7 F4點故障時|Zcd|的測量值 表2列出了當Line1為電纜線路時,在系統不同位置發生故障時|Zcd|的穩態測量值。從表2可以看出,當線路發生區內大過渡電阻接地故障時,故障線路|Zcd|的測量值與第1節理論分析符合,基本接近2Rf或4Rf,|Zcd|值相對于ZC較小,最大值為2 025 Ω。當區外發生故障時,其數值大于5 kΩ。可見,使用判據式(11)可以很容易地區分線路區內、區外故障,因此基于正序和商阻抗的縱聯保護原理可以應用于含IIDG的配電網線路。 圖 8 F2點故障時|Zcd|的測量值 故障類型Rf/ΩZcd1/ΩZcd2/Ω無故障-252 9246 974區外故障F2F3F4F5ABCABCBCACGABCABCBCACGABCABCBCACGABCABCBCACG0.01110200.01110200.01110200.0111020249 606249 614251 374250 916249 932249 371251 380251 068249 496249 478251 062250 819>349 310252 679252 733252 4466 9566 9576 9786 9766 9616 9566 9766 9686 9576 9596 9786 974>5 7396 9366 98396 9739區內故障F1ABCBCBCGABCGACGABCG0.011101005005000.053.0139.571972 0251 0010.053.0239.771981 936990 注:|Zcd|1、|Zcd|2分別為模型1和模型2中|Zcd|的測量值 本文提出一種基于正序和商阻抗的縱聯保護新原理,并進行了理論分析和PSCAD/EMTDC仿真驗證。理論分析和仿真結果表明:區外發生故障時,新原理的動作量反映線路容抗,其數量級為kΩ;區內發生故障時,忽略線路電阻時動作量反映2倍或4倍的過渡電阻值,二者數值差別較大,保證了基于正序和商阻抗的縱聯保護的靈敏性。該原理適用于含IIDG的配電網保護,具有容易整定、動作靈敏、抗過渡電阻能力強的優點。仿真結果驗證了新原理的有效性。2 正序和商阻抗算法的性能分析
2.1 耐受過渡電阻能力分析
2.2 受暫態分量的影響分析
2.3 受IIDG控制策略的影響分析
2.4 DG出力干擾分析
2.5 空載合閘分析
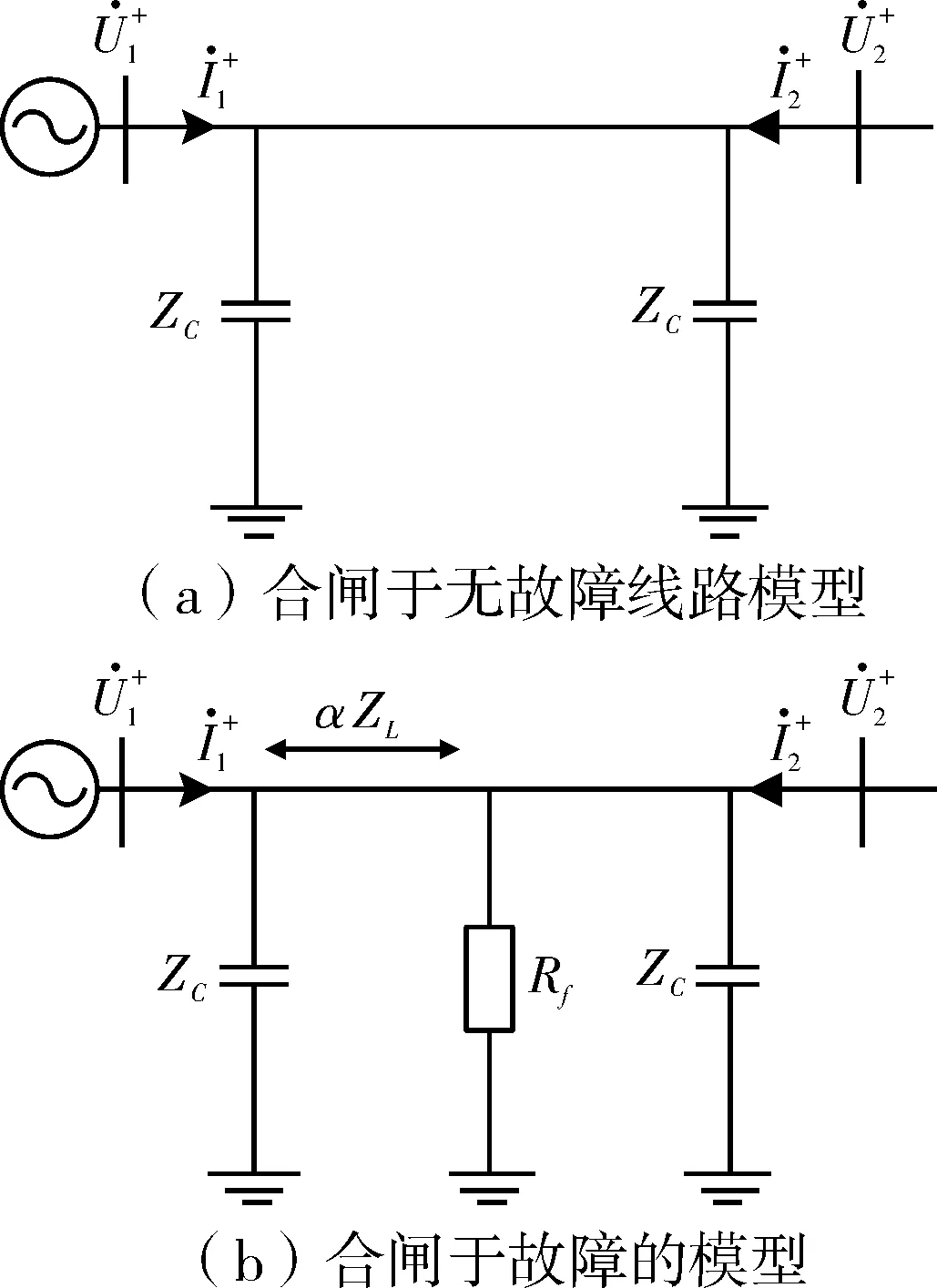
3 仿真驗證
3.1 仿真結構及參數
3.2 仿真結果





4 結論

