碳微球的納米壓痕彈塑性行為的研究

孫 淵， 張 棟， 孫 利

(上海電機學院 機械學院, 上海 201306)

碳是自然界中分布非常普遍的一種元素，碳質產品己成為現代科技中無法替代的材料。依據反應的前驅體、合成方法與工藝參數的不同，可以制備碳微球、碳納米管、碳纖維、錐形碳管及富勒烯等結構與性質差別顯著的新型碳材料。其中，碳微球因其本身具有的潛在優越性，如高導熱系數和電導率、良好的耐熱性能、優異的化學穩定性與自燒結性能等，這些優異特性使其成為一種高性能的功能材料，可應用于鋰離子電池中作為電極材料、催化劑載體、電化學電容器材料、活性碳球吸附材料[1-5]等。目前，各位學者通過化學氣相沉積法、溶劑熱法和模板法等制備了粒徑大小與結構不同的碳微球材料，并通過光學顯微鏡，X射線等手段進行組織表征和性能研究[6-10]。文獻[6]通過簡單的化學氣相沉積法從甲苯材料中制備了碳球，通過改變成分和混合氣體的流動速率得到了直徑在60 nm～1 μm之間的碳微球，并通過掃描電鏡、X射線、能量彌散X射線譜，紫外激光拉曼光譜等手段分析其形貌，所得到的碳球由表面光滑、尺寸均勻，含有90%以上的石墨碳組成。文獻[7]以甲苯、乙炔為碳源，利用化學氣相沉積法合成均勻，得到較好表面質量的非晶碳球，并通過場發射掃描電子顯微鏡，X射線和高分辨率的透射電鏡分析了其組織形貌。文獻[8]通過不同的工藝并利用糖醇制備成尺寸在260 nm～1.5 μm的碳微球，并說明表面活性劑和硫酸處理在制備不同尺寸的碳微球中起到關鍵的作用。文獻[11]研究了碳微球的電化學性能，由于其比電容特別高可應用于高能量和高功率密度的超級電容器中的電極材料。

綜上所述，國內外在各種碳微球的制備、組織表征、電化學性能研究以及應用上已取得了不少成果，但是很少涉及到碳微球的彈塑性力學行為的研究，因此，本文主要研究1 μm碳微球的壓痕彈塑性行為，探討在載荷下的壓入響應，由于碳微球尺寸微小，要充分考慮基體效應對測試結果的影響，為1 μm碳微球的進一步研究與應用提供參考。

1 試 樣

試樣材料為碳微球，通過葡萄糖制備而成的1 μm的顆粒，這些顆粒包埋在環氧樹脂中，然后通過機械磨削和拋光，達到表面質量均勻的半球，通過光學顯微鏡和原子力顯微鏡可以看出其微球的分布，如圖1所示。經過機械加工后，得到在不同截面上的微球，展現出不同的尺寸，均由1 μm及以下尺寸組成，為納米壓痕提供足夠的壓痕區域。

圖1 1 μm的碳微球顆粒

由于碳微球的尺寸較小，從而限制了納米壓痕加載載荷的大小，如果載荷過大，在載荷作用下所形成的壓痕深度大于小球的1/10，則所測量的結果會受到周圍材料的影響，即基體效應。本文將利用納米壓痕法研究小球的響應行為，探討在不同壓痕深度下其基體效應的影響程度。

納米壓痕儀為Nano IndenterII，其型號為Hysitron TriboScope，并具有美國Quesant公司的原子力顯微鏡進行圖像觀察和掃描，所用的壓頭為金剛石Berkovich壓頭，采用載荷模式加載，每一個載荷下重復進行壓痕實驗至少5次,加載時間、停留時間和卸載時間分別為10 s、2 s和10 s，通過壓痕實驗可以得到載荷-位移(P-h)曲線，在此基礎上計算接觸彈性模量、彈性回彈量、回彈率和彈性回復能等壓痕彈塑性行為，并且通過P-h曲線得到在最大載荷Pmax下的最大壓痕深度hmax，卸載后由于彈性回復而殘留壓痕深度hf。

2 結果與討論

2.1 P-h曲線

通過納米壓痕法，得到了1 μm碳微球在載荷范圍為15～150 μN下所對應的P-h曲線。通常，壓痕尺寸一般是試樣尺寸的1/10，在載荷50 μN作用下，最大壓痕深度基本達到56 ～59 nm范圍之內，滿足壓痕實驗要求。但是在載荷75 μN作用下，最大壓痕深度達到80～86 nm之間，最大壓痕深度與碳微球半徑比值(hmax/R)為0.16～0.17之間，基本上不能滿足實驗要求，所測試的值受到周圍基體的影響。圖2所示為碳球的P-h曲線和基體的P-h曲線，如果沒有足夠的壓痕區域，碳微球的壓痕行為將受到基體的影響，因為基體的彈性模量和硬度遠遠小于碳微球，產生較大的彈性變形和塑性變形，P-h曲線中加載曲線與卸載曲線所包容面積也就越大，對于載荷100 μN、125 μN、150 μN，其曲線所包容面積逐一明顯增加，抗變形能力下降，塑性變形程度逐步增加。通過P-h曲線，可直觀地描述載荷作用下的壓痕行為，在最大載荷下的最大壓痕深度，和卸載后即載荷為0時，由于塑性變形而形成的不可恢復的殘留壓痕深度hf。圖3描述了在載荷作用下的最大壓痕深度與殘留壓痕深度的關系，最大壓痕深度、殘留壓痕深度均隨著載荷的增加而以不同的斜率增加。特別是在載荷大于50 μN時，其殘留壓痕深度急劇增加，說明碳微球由于受到環氧樹脂基體的影響，基體的彈性模量和硬度遠遠小于碳微球的，故將產生較大的塑性變形。

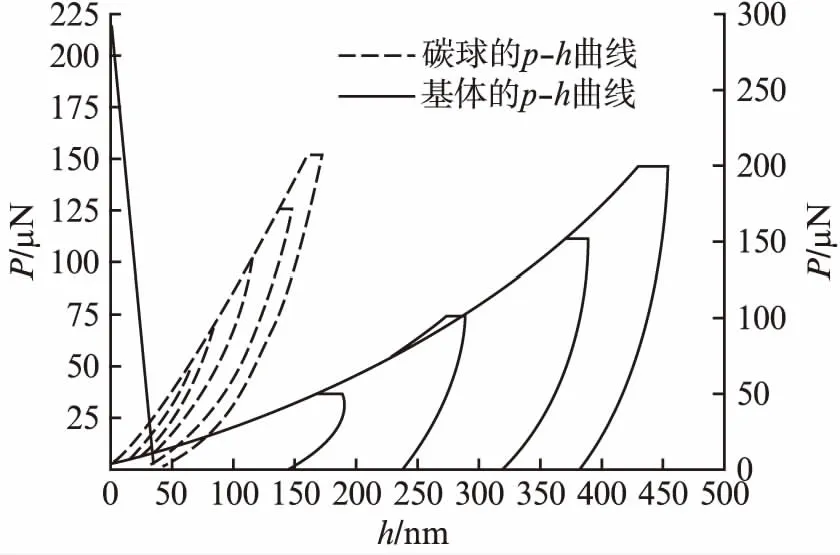
圖2 碳微球的P-h曲線和基體的P-h曲線

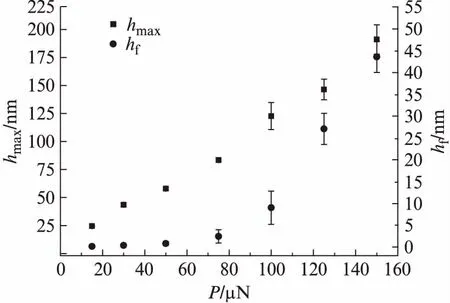
圖3 最大壓痕深度和殘留壓痕深度

2.2 彈性模量及基體效應

卸載后，試樣表面試圖要恢復到原來形狀，但是由于塑性變形而產生形變，彈性應變存在一定程度的回彈，因此，基于P-h曲線，根據卸載初始部分的響應可以估算材料的彈性模量，一般是在最大載荷處基于卸載曲線的斜率來計算，與斜率dP/dh和接觸面積A有關[12]。彈性模量為

(1)

對于Berkovich壓頭，端部的角度θ=65.27°時，則其接觸面積為

(2)

式中：hc為壓痕接觸深度，即卸載曲線頂部切線(接觸剛度S=dP/dh)和橫軸的交點。其值為

(3)

式中：ε為一個依賴于壓頭幾何形狀的常數，對Berkovich壓頭，ε=0.75。

聯立式(1)～(3)，彈性模量與P-h曲線中參數有關，其值為

(4)

碳微球是測試對象，用于包埋的環氧樹脂為基體，在壓痕實驗中，當不滿足壓痕實驗要求時，基體的性能將會影響碳微球性能的測量結果，這就是所謂的“基體效應”，在文獻[13-16]中指出，在基體的彈性模量小于試樣顆粒的彈性模量5倍、硬度5倍的情況下，當hmax/R<0.02時，壓痕所測試的試樣顆粒即碳微球的彈性模量與有限元分析值誤差較小；當0.020.5時，被測顆粒即碳微球的彈性模量將接近于基體的彈性模量。在本次實驗中，根據實驗結果進行分析，如圖4所示。隨著載荷的增加，最大壓痕深度也隨著增加，hmax/R的比值也隨著增加，所測碳微球的彈性模量隨著hmax/R的增加而減少，其誤差也隨之增加，體現出“基體效應”。

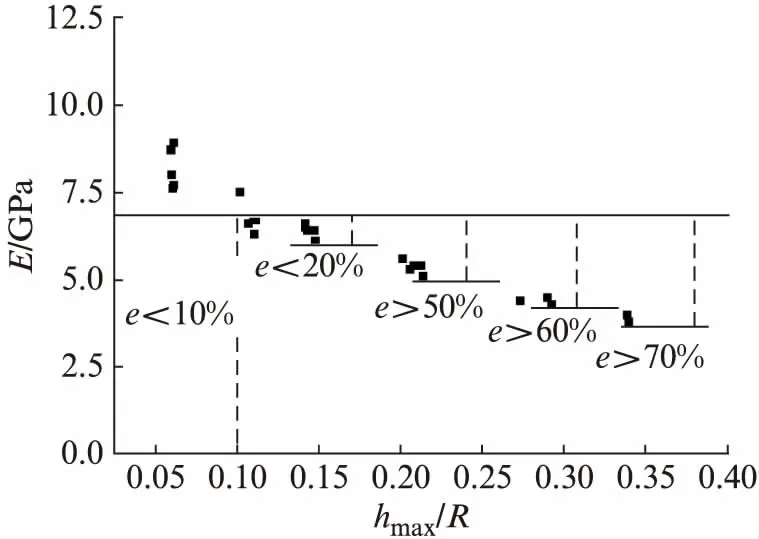
圖4 彈性模量與hmax/R關系圖

2.3 彈性性能

卸載后，由于材料的彈性回彈和能量釋放，將產生一定的回彈量δ=hmax-hf，其彈性回彈率ζ=δ/hmax，圖5描述了碳微球在載荷作用下的回彈量和回彈率的變化，回彈量均隨著載荷的增加而增加，當載荷小于50 μN之內，回彈率基本穩定，其值高達99%；隨著載荷的增加，碳微球的回彈率逐漸下降，在載荷125 μN、150 μN下，回彈率急劇下降至81%、75%。

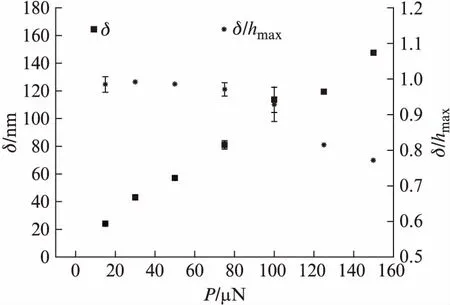
圖5 回彈量與回彈率在載荷作用下的變化圖

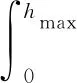
塑性能反映了材料儲存能量的大小，而彈性能反映了材料的彈性回彈能量的大小，可通過彈性能量回復率描述材料回彈能力，即彈性能與總能量之比η=Ee/Etotal。圖6描述了微碳球的彈性能和彈性回彈能力，彈性能隨著載荷的增加而增加；在載荷50 μN之內，彈性能量回復率基本恒定，隨著載荷的增加逐漸下降；在載荷150 μN作用下，彈性能量回復率下降為0.45，說明在較高載荷下產生了較大的不可回復的塑性變形和儲存了較大的塑性能。

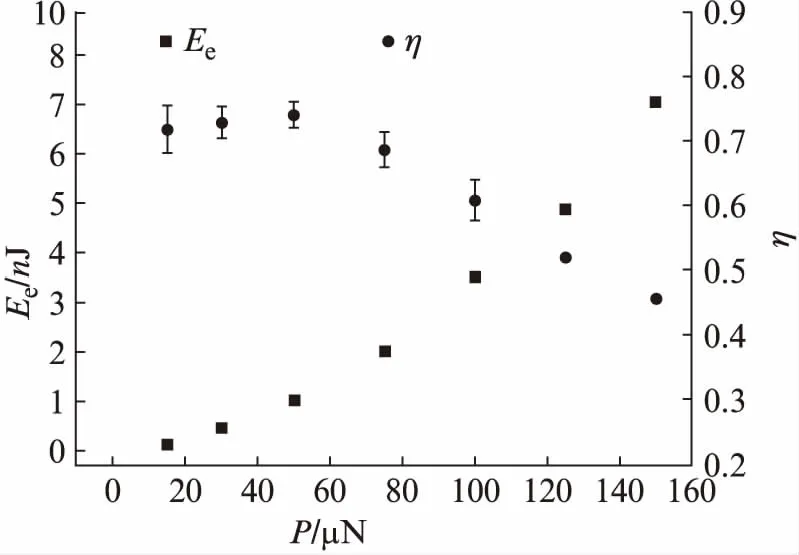
圖6 彈性能與彈性能量回復率在載荷作用下的變化圖

3 結 論

碳微球由于其高導熱系數和電導率、良好的耐熱性能、優異的化學穩定性等，成為一種新型的功能型材料，1 μm的碳微球包埋于環氧樹脂中,采用壓痕法研究了其納米壓痕行為以及壓入響應，分析了載荷作用下最大壓痕深度、彈性回彈量、接觸剛度、彈性能和彈性回彈能力等彈性性能，在hmax/R超過0.1時，由于基體效應，所測得的碳微球的接觸彈性模量值將產生一定的誤差，隨著載荷的增加，hm/R增加，誤差也隨著增加；在載荷75 μN下，hm/R為0.16～0.17時，所測得的接觸彈性模量值誤差將接近50%；當hm/R>0.5時，被測顆粒的彈性模量將接近于基體的彈性模量，碳微球的彈性回彈率、彈性能量回復率隨著載荷的增加而逐漸下降，碳微球將發生較大塑性變形并儲存了較大的塑性能。