基于自適應觀測器的風機變槳系統故障診斷

宋昌舉， 文傳博

(上海電機學院 電氣學院， 上海 201306)

風能，作為當前一種清潔、可再生能源，已成為人們解決能源缺乏問題不可或缺的力量[1]。風力發電是有效利用風能的最主要形式，對于一些風電設備安裝在高山和海邊等比較惡劣的環境中，風力發電系統運行十分復雜，當系統出現參數不確定時，對系統的控制將更加復雜[2]。因此，對風機可能產生的故障進行快速有效地估計，確保風力發電系統能安全可靠地運行具有重要意義。

變槳系統故障在風電機組的運行故障中發生率較高[3]，風電機組變槳系統故障主要有傳感器故障、齒輪箱故障及軸承故障等，傳感器是變槳系統中最基本的元件，也是最容易發生故障的[4]。如果故障傳感器的輸出信號被用于系統控制器的輸入，將會對閉環反饋控制產生影響，使風力發電系統輸出異常，導致系統性能降低[5]。變槳系統能否穩定運行，在很大程度上會受到風速的影響，當風速發生改變時，槳距角傳感器根據風速的變化，可以實時將槳距角變化的信息傳遞給控制器，由控制器及時地發出改變槳距角的指令信息，并通過執行機構迅速動作，調整槳距角，來保證風機的穩定運行。因此，對系統中傳感器單元進行實時故障檢測顯得尤為重要。

當前的幾類故障檢測方法有基于解析模型[6-7]、基于信號處理方法[8]以及基于知識的方法[9]。其中，基于解析模型的方法中，觀測器法又是應用最為廣泛的，可以對產生的各類故障進行準確估計[10]。近年來，基于觀測器的故障診斷方法受到了很多關注，文獻[11]提出了一種基于未知輸入狀態觀測器的設計方法，卻在實際的應用方面有一定的局限性；文獻[12]是將文獻[11]設計觀測器的方法應用于風機執行器的故障診斷中，但是其輸出只能為確定的情況；文獻[13-14]采用的是基于滑模觀測器對傳感器的故障檢測，僅僅是對狀態方程為線性且沒有未知參數的情況下的觀測器設計；劉聰等[15]將自適應算法與滑模觀測器相結合，研究了執行器和傳感器故障重構的問題，但是不能保證觀測器穩定性。本文針對風機變槳系統的執行機構故障和傳感器故障問題，提出一種基于自適應解耦觀測器的故障診斷方法，主要通過兩個方面設計出理想的故障診斷方案：① 對未知干擾因素具有魯棒性；② 對故障信號具有較強的靈敏度。考慮到建模誤差、噪聲等不確定因素，將這些不確定因素統一作為系統的未知輸入干擾矩陣，設計一種基于解耦形式的自適應觀測器。該方法通過解耦處理技術使系統的狀態方程不再含有未知故障向量，使系統的故障估計和狀態估計的求解得以分開，通過得到狀態估計和測量輸出后，對系統的故障向量進行估計，從而產生了對擾動因素不敏感而對故障量非常敏感的殘差信號，利用此殘差信號的閾值評價函數，建立故障決策邏輯，對系統進行故障檢測。

1 風機變槳系統建模

變槳系統是風力發電機正常運行的重要環節之一，風力發電機組能否正常工作與變槳系統能否穩定高效的運行有著重要聯系，而變槳系統中，槳距角傳感器和變槳系統執行機構則是保證變槳系統正常工作的重要器件。

根據變槳系統運行原理進行動力學分析，如圖1所示。

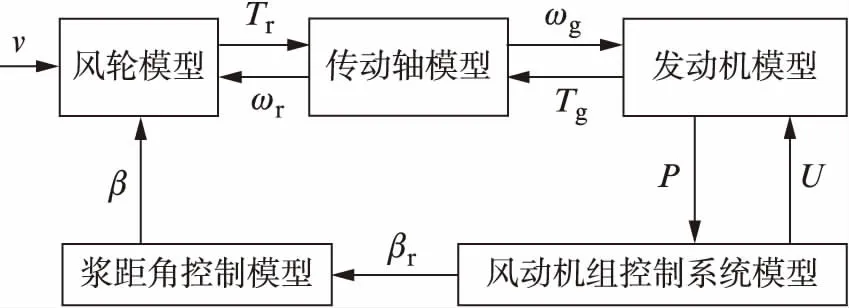
圖1 風機液壓變槳系統動力學模型

圖1中，v為空氣進入風輪前的實際風速；Tr為主傳動軸轉矩；Tg為發電機轉矩；ωr為主傳動軸轉速；ωg為發電機轉子的實際轉速；P為發電機的實際發電功率；U為控制系統的控制電壓；β為槳距角；βr為槳距角的測量值。

在不影響模型精度的條件下，忽略液壓缸的內部摩擦和部分負載，僅對含有噪聲、干擾等不確定因素和系統故障的液壓變槳系統進行故障模型的建立，并將系統的未知不確定因素統一歸并到一起，用干擾信號矩陣d(t)表示。根據系統的動力學模型，可建立變槳系統故障模型如下：

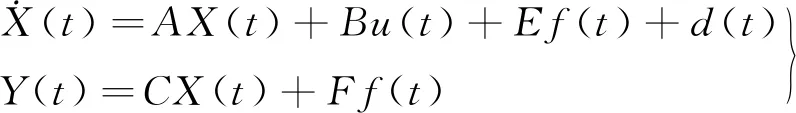
(1)

式中：X(t)=[βωgωgm]T；u(t)=[βr]；d(t)=[v,U]T；X、Y、u分別為系統的狀態向量、系統輸出向量和系統控制輸入向量；ωgm為發電機轉速測量值；A、B、C均為常數矩陣；E、F均為已知的故障分布矩陣；f(t)為故障特征向量，是待估計的定常向量，可表示f(t)=[f1(t)，f2(t),…fn(t)]T，則f(t)的每個分量分別為該系統中不同故障類型。f(t)=0時，表示沒有故障；f(t)≠0時，表示發生故障。Ef(t)和Ff(t)分別為系統的執行機構故障和傳感器故障。

2 解耦自適應觀測器設計與穩定性分析

2.1 問題描述

根據變槳系統的故障模型，并結合解耦形式的自適應觀測器設計原理，對系統進行重新描述如下：

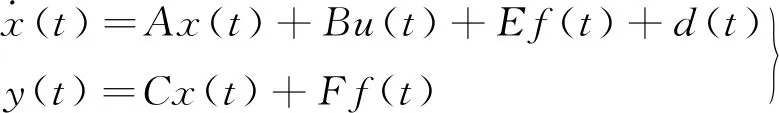
(2)

式中：x(t)∈Rn為系統的狀態向量；u(t)∈Rr為系統的控制輸入向量；y(t)∈Rm為系統輸出向量；A∈Rn×m，B∈Rn×l，C∈Rm×n均為為常數矩陣；E∈Rn×p，F∈Rm×p均為已知的故障分布矩陣；f(t)∈Rp為未知故障特征向量，是待估計的定常向量。

2.2 解耦自適應觀測器設計

對系統構造自適應觀測器得

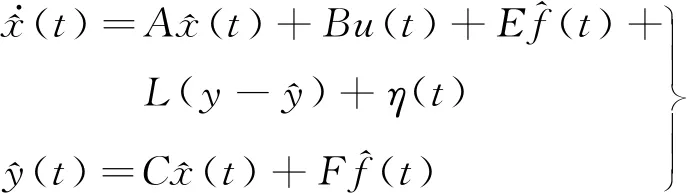
(3)

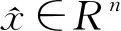
定義狀態估計誤差

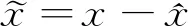
故障估計誤差

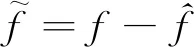
則有

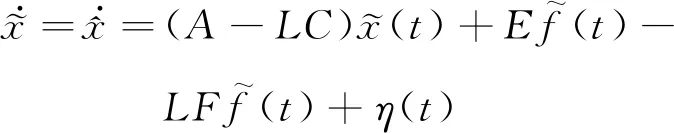
(4)

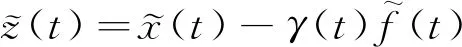
(5)

式中：γ(t)∈Rn×p為待設計矩陣。

由式(4)和式(5)可知：

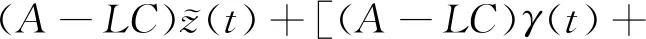
(6)

為簡化式(6)，可以將待定的參數γ(t)、η(t)選擇如下取值：

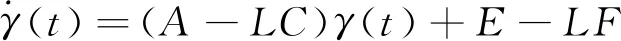
(7)

(8)

將式(7)和式(8)代入式(5)可簡化為

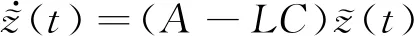
(9)

再由式(8)代入式(3)可得：

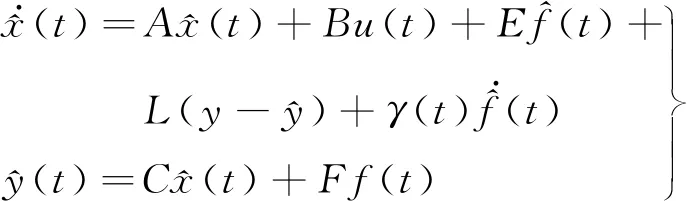
(10)

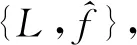
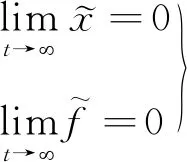
(11)

令Δk=A-LC，則自適應觀測器增益矩陣的選擇應該滿足

(12)

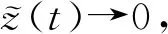
(13)

式中：K為待設定的時變矩陣。

從而可知故障估計誤差方程為

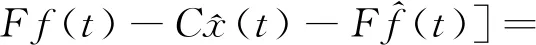
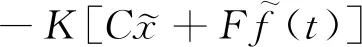
(14)

將式(5)代入式(14)得

(15)

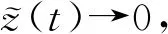
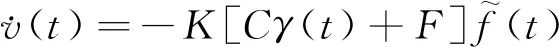
(16)

當選擇：

K=Γ[Cγ(t)+F]T

(17)

其中，Γ∈Rp×p為任意的正定矩陣，則可使式(16)收斂，具體證明在下一節的觀測器穩定性分析中。

將式(17)代入式(13)中，得到故障估計狀態方程為

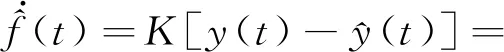
(18)

接著將通過上述推導，對自適應觀測器進行解耦形式的變換。結合式(5)和式(7)對式(2)進行變換后得到解耦后的新系統為

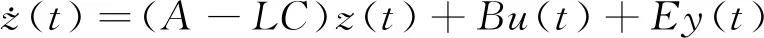
y(t)=Cz(t)+[Cγ(t)+F]f(t)

(19)

通過解耦變換后的新系統具有的優點：通過解耦處理后，系統的狀態方程不再含有未知故障向量，使得系統的故障估計和狀態估計的求解得以分開，有利于先得到狀態估計和測量輸出后，再對系統的故障向量進行估計。

通過式(12)設計增益矩陣L，使得(A，C)具有一致可觀性，即其狀態z(t)穩定。

狀態z(t)的估計方程為

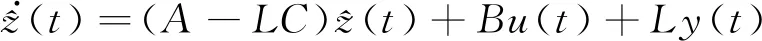
(20)

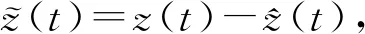
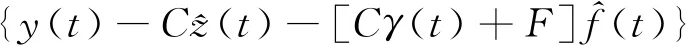
(21)

根據式(7)、式(20)、式(21)可確定解耦自適應觀測器設計方程為

(22)

2.3 觀測器穩定性分析

本章所設計觀測器的方法與第3章中自適應觀測器的證明過程相比，減少了比較嚴格的Lipschitz函數條件，使得解耦后的自適應觀測器設計要求的自由度更高，對故障系統的應用也就更加的廣泛。

對解耦后式(19)設計自適應觀測器的穩定性分析需要作如下假設。

假設1式(19)中的矩陣E、F均為有界且分段連續。

假設2針對矩陣(A,C)，存在有界的時變增益矩陣L(t)，滿足式(12)時，使得式(9)穩定。

假設3由矩陣E、F組成的線性濾波器(H(t)∈Rm×p)為

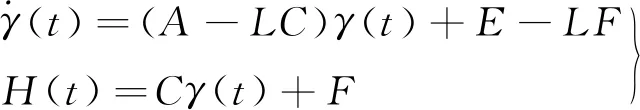
(23)

其中，將γ(t)和H(t)作為該濾波器的正常狀態和輸出。假設存在正常數α、T,對所有的t≥t0，使如下不等式成立，即

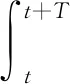
(24)

式中：Ip為單位矩陣。

引理1存在正常數α、T,對所有的t≥t0，使得不等式(24)成立時，則系統

(25)

是穩定的。其中，Γ∈Rp×p為任意的正定矩陣。

引理2若如下系統穩定

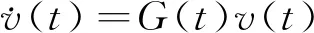
(26)

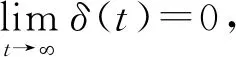
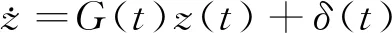
(27)

也是有界且收斂于0，其中，若δ(t)為快速的指數收斂，那么z(t)也是可以快速收斂的。

根據以上假設和引理，可以得出如下定理:

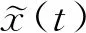
證明由上一節自適應觀測器設計過程可知，狀態z(t)和故障參數f(t)的誤差狀態聯立方程為

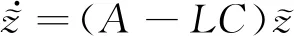
(28)

(29)

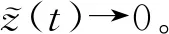
令式(29)的后半部為

(30)

又由式(5)可知：

(31)

3 殘差設計及仿真分析

3.1 殘差評價函數設計

殘差是系統的實際輸出與狀態觀測器輸出的差值,反映實際系統與系統數學模型之間不一致程度的一個量。變槳系統的殘差主要由系統的干擾和故障確定,假設風機系統的殘差表達式為

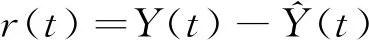
(32)

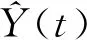
要設計殘差的評價函數，就必須先考慮殘差閾值的設計，在變槳系統中，考慮到在系統發生故障時，可能存在未知輸入擾動的原因，對系統的輸出信號的測量值會受到較大影響，為了克服干擾的影響，引入殘差的均方根函數表達式為

(33)

式中：JRMS表示殘差信號r(t)的均方根值。則定義閾值為

(34)

根據以上故障決策邏輯為

當|r(t)|>Jth,RMS，系統發生故障，報警。

當|r(t)|≤Jth,RMS，系統未發生故障，不會報警。

3.2 仿真結果與分析

為驗證基于觀測器方法故障診斷的有效性，對系統(1)中的部分系統矩陣和參數選取如下：

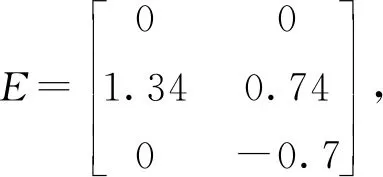
(1) 當變槳系統執行機構發生故障時，故障矩陣F=0，取執行機構在t=10 s時，發生幅值變化的跳變故障，根據殘差的閾值評價函數，計算出故障診斷的閾值Jth,RMS=0.658 8，即當|r(t)|>Jth,RMS，診斷系統發生故障。仿真結果如圖2、圖3所示。

圖2 執行器故障幅值估計

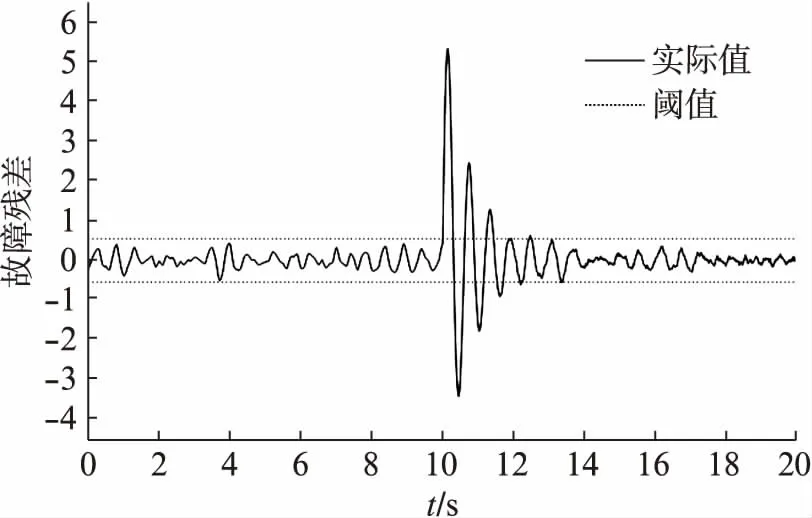
圖3 故障殘差與閾值對比

由圖2可見，所設計的解耦形式的自適應觀測器能夠很好的反映變槳系統在發生執行機構故障前后的實際情況，具有較好的跟隨性，并且估計的故障值能準確反映系統的變化。由圖3可知，根據設定的閾值，系統故障殘差r(t)的值在t為10—11 s左右超出閾值范圍，說明基于自適應觀測器方法能檢測出風機變槳系統的執行機構發生了故障。

(2) 當系統發生傳感器故障時，系統方程中的故障矩陣E=0,假定槳距角傳感器正常工作式f=0，當傳感器發生信號丟失故障時，取傳感器分別在t=3 s、t=7 s、t=10 s、t=15 s發生故障，具體故障描述如下：

接著根據殘差的閾值評價函數，計算出故障診斷的閾值Jth,RMS=0.459 8，即當|r(t)|>Jth,RMS，診斷系統發生故障。仿真結果如圖4、圖5所示。

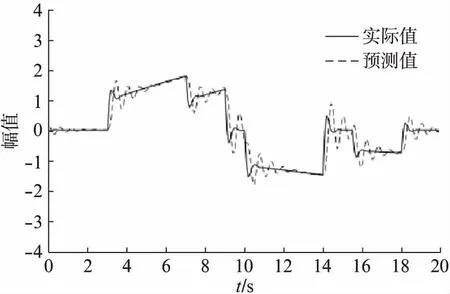
圖4 傳感器故障幅值估計

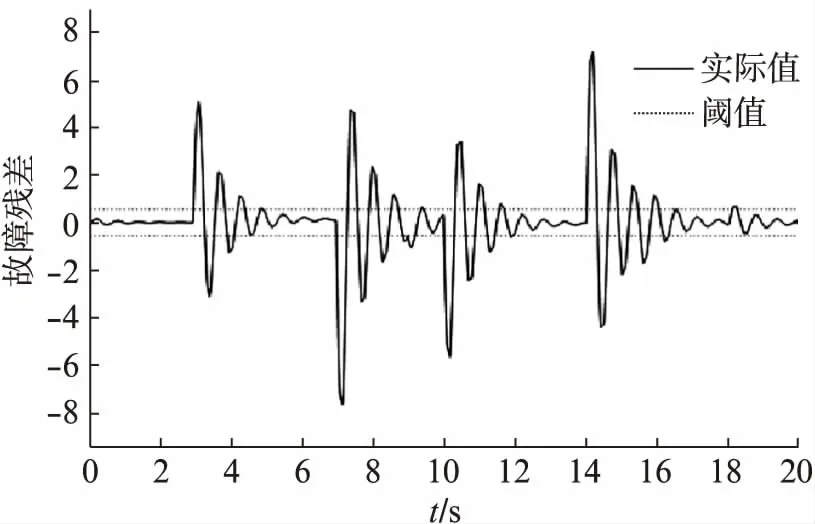
圖5 故障殘差與閾值對比

由圖4可見，所設計的解耦形式的自適應觀測器也能夠很好地反映變槳系統在發生傳感器故障前后的實際情況，在多次故障發生時也能準確反映系統的變化，具有很好的收斂性與跟隨性。由圖5故障殘差和閾值的對比可知，通過設定的閾值，可以有效地檢測出系統故障的發生，對于傳感器多次發生故障也可及時檢測，說明基于自適應觀測器方法能檢測出風機變槳系統的傳感器故障的發生。

4 結 語

本文將自適應觀測器設計方法和解耦處理方法相結合，針對風機變槳系統的故障診斷問題，提出了一種解耦形式的觀測器設計，通過對系統方程進行解耦設計后，系統的狀態方程不再含有未知故障向量，使系統的故障估計和狀態估計求解得以分開，有利于通過先得到狀態估計和測量輸出后，再對系統的故障向量進行估計，由仿真結果可以看出，通過設計的解耦觀測器，對具有干擾等不確定因素的復雜變槳系統故障問題，可準確有效地檢測和估計故障，對故障幅值的變化也有很好的跟隨性。