含分布式能源的電網優化調度研究
張 倩, 張延遲, 解 大
(1. 上海電機學院 電氣學院, 上海 201306;2. 上海交通大學 電子信息與電氣工程學院, 上海 200240)
據統計,2018年,國家電網26家省公司積極開拓綜合能源服務市場,累計實施2 943個項目,實現綜合能源服務業務收入49億元,同比增長了133%[1]。從業務領域來看,實施綜合能效服務項目數量最多,占比73%,分布式能源服務項目占比9%。
隨著售電側的放開,大批能源服務商自建分布式能源,在自給自足的同時,也實施余電上網,拓展企業新的利潤增長點。開發的電力市場賦予需求側用戶以購電主體和售電主體雙重身份參與電網的雙向互動。博弈論作為解決2個及以上的決策主體之間利益關聯問題的重要工具[2-4],在電力系統規劃、電力市場方面應用已久。文獻[5-6]介紹了將谷諾博弈模型(Cournot duopoly model)和伯特蘭德博弈模型(Bertrand duopoly model)運用于發電公司競價上網的問題。文獻[7-8]討論分析了非合作博弈和斯塔克爾伯格博弈模型(Strackel-berg leadership model)運用于售電公司將儲能反向售電給電網的情景;文獻[9]設計了N人非合作博弈框架,討論了居民用戶售電商在分布式能源與儲能的運行管理方面的作用;文獻[10-11]介紹了演化博弈論的均衡分析方法運用于電力大用戶與發電公司之間的直接交易情況。
本文介紹了博弈論的基本理論,分析了售電側改革對需求側博弈行為的影響,重點討論了以能源服務商為群體與電網的博弈關系以及各能源服務商之間博弈行為,以此達到電網和能源服務商之間的收益平衡。
1 對需求側博弈行為的影響
1.1 能源服務商的影響
為了主動適應能源供給側改革和電力體制改革的新要求,國家發改委發布的《關于做好2018年降成本重點工作的通知》提出,要合理降低用能成本,支持有條件的企業自建分布式能源,支持新能源發電與用能企業就近就地進行交易。
新電改鼓勵發展能源服務業務,支持能源服務商自建分布式能源,參與電力市場交易競爭,從而豐富了需求側的用戶類型,從單一的用電用戶向購售電用戶轉變,增加了需求側的博弈行為,建立起能源服務商群體與電網之間的博弈關系。
1.2 分布式能源發展的影響
新電改提出綠證交易,鼓勵開發和發展可再生能源,但是分布式可再生能源受諸多因素影響,如地理位置、規模大小和天氣環境等,其輸出功率具有明顯的波動性、隨機性和間歇性,影響電網的功率平衡,降低其供電的穩定性和可靠性。
因此,一方面自帶分布式能源的能源服務商可以作為售電方參與市場博弈,另一方面電網也需要考慮分布式能源接入電網,使電力系統尤其是配電網面臨一些新問題,在追求電網收益最大的同時,也需保證電力系統安全可靠的運行。
1.3 博弈行為的轉變
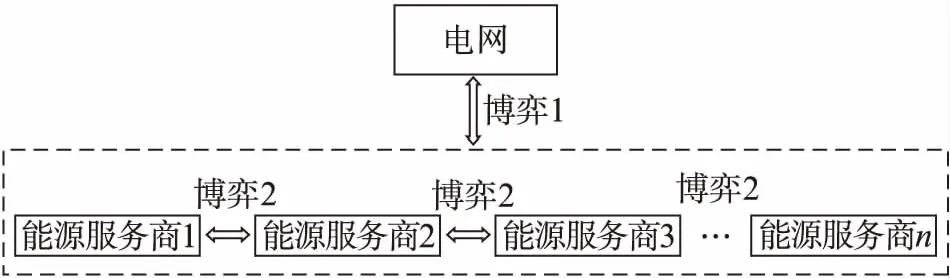
根據《推進售電側改革的實施意見》,電力市場交易方式從單一的由電網公司統購統銷向用戶自主選擇售電主體轉變[12],售電側市場主體不再局限于傳統的電網企業,還包括了售電公司和能源服務商。隨著售電側改革的推進,需求側出現了新的博弈行為(見圖1)。在電力市場改革前,電網公司與售電公司存在單一博弈關系,即博弈A,但是所有的銷售電價和交易模式都是由電網公司制定,用戶并不參與任何售電行為;博弈B表示電力大用戶直接與發電公司進行購電交易,以此省去中間環節,降低購電成本;博弈C表示中低能用戶與電網公司或售電公司進行購電交易,例如商業、居民等中小型用戶可以在電力市場中自主選擇售電主體,彼此之間存在博弈行為;博弈D表示自建分布式能源的能源服務商在自給自足的情況下,余電上網,以售電主體的身份與電網進行交易,兩者之間存在利益沖突。
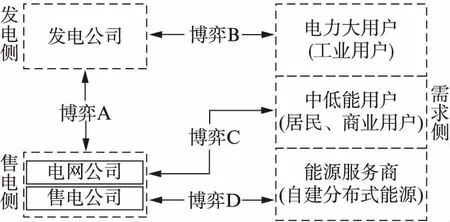
圖1 電力市場博弈行為
2 博弈模型
在售電側改革的大背景下,本文主要討論由新電改產生的能源服務商(具備分布式能源發電的能力,具有售電和用電的雙重身份)群體和電網公司之間的博弈行為,以及能源服務商個體之間的博弈關系。
2.1 博弈理論
一個博弈格局包括參與者、策略空間和支付函數,其中,參與者為決策主體,一般為兩個及其以上,用N={1,2,…,n}表示一個含多名參與者的集合,Si表示參與者i(i∈N)的策略集合,S={s1,s2,…,sn}表示所有參與者的策略組合,支付用于衡量參與者之間博弈所獲的收益,U={u1,u2,…,un}。
2.2 電網與能源服務商群體的博弈模型
2.2.1 雙方拍賣 將多個能源服務商作為一個群體來與電網公司進行交易,一般經歷4個階段:電網公司確定分布式能源上網的電量,雙方雙向報價,序貫報價、交易成功或失敗。但是這一切交易是在確保電網安全穩定的大前提下進行的,如果交易電量不滿足安全校核的條件,則需要電網公司重新確定分布式能源并網的電量,交易流程見圖2。
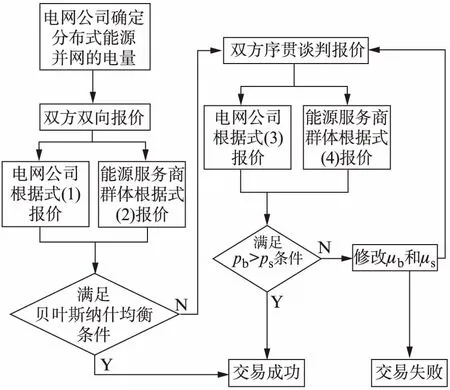
圖2 交易流程圖
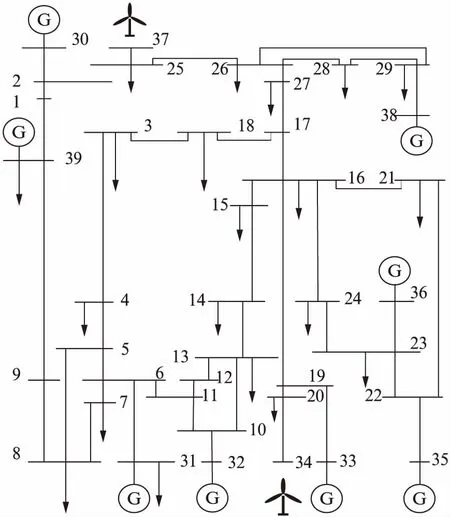
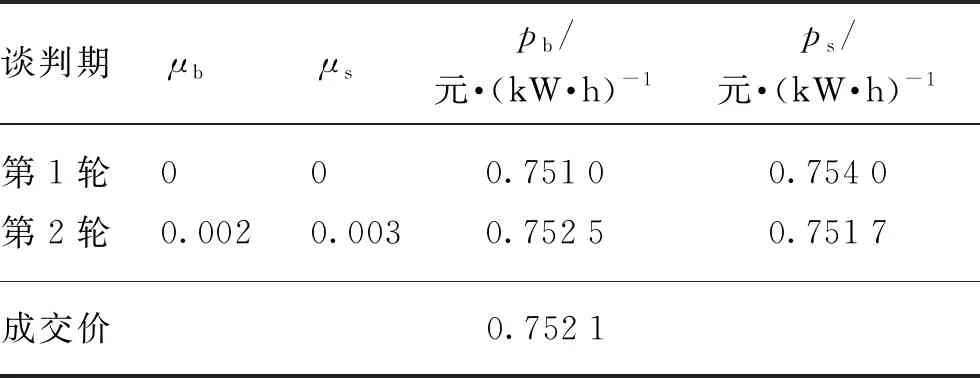
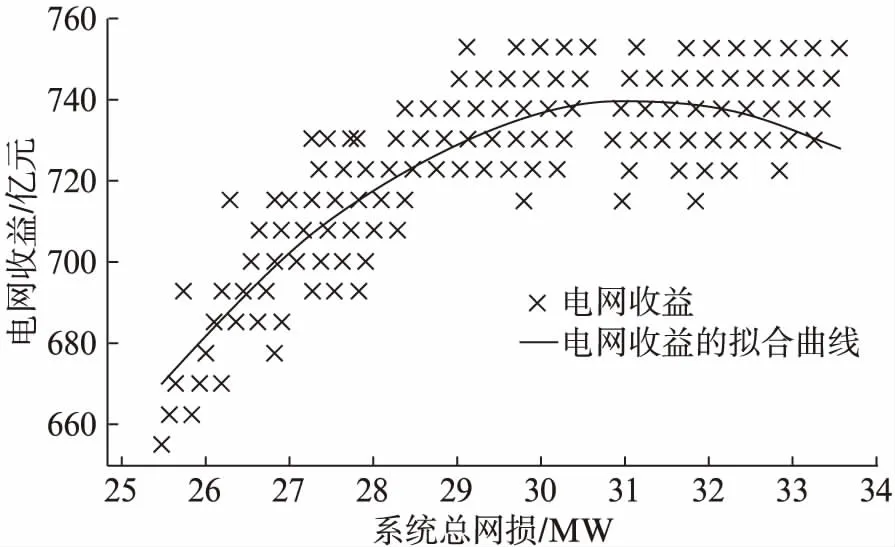
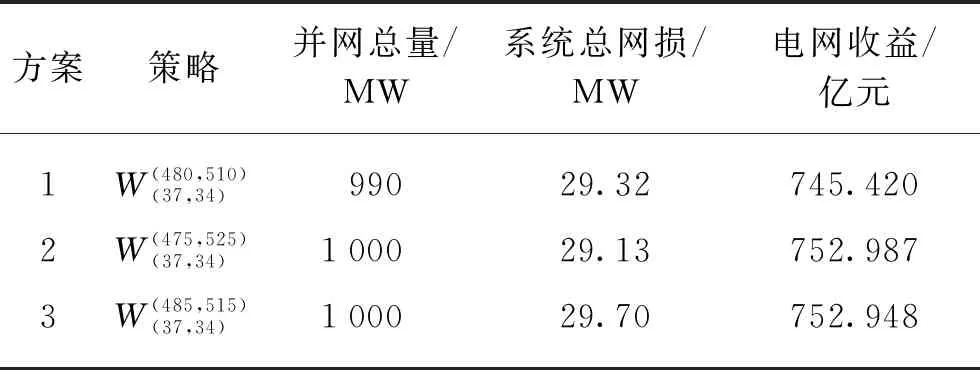
在雙方拍賣的交易博弈中,電網公司對該對象的估價為vb,能源服務商群體對該對象的估價為vs,電網公司確定一個買價為pb,能源服務商群體確定一個賣價為ps,若pb≥ps,則交易以p=(pb+ps)/2的價格進行,若pb 由貝葉斯納什均衡定理[14]推導可知,只要滿足pb、ps在一定條件下的最大化,則策略{pb(vb),ps(vs)}即可達到貝葉斯納什均衡,有: Prob{pb≥ps(vs)} (1) Prob{pb(vb)≥ps} (2) 表1 雙方報價表 則電網公司第2輪出價pb2應該滿足 (3) 式中:pb*為能源服務商群體能接受的二次報價。 于是發電商群體第2輪出價ps2應該滿足 (4) 式中:ps*為電網公司能接受的二次報價。 由推導可得: (5) (6) 2.3.1 收益函數 文中討論的是2層模型(見圖3),第1層模型是電網公司與能源服務商群體的博弈關系(即圖1中的博弈D,此處定義為博弈1),以能源服務商群體的收益為目標,結合分布式能源上網的價格政策得出價格區間。第2層為能源服務商之間的博弈關系(博弈2),但不是簡單的能源服務商個體之間的價格博弈,而是構建電網收益函數,由電網公司給出某時段電網可以接納分布式能源上網的總電量,各能源服務商個體在價格區間內自由報價競爭,計算總體收益,在電力系統約束條件內達到電網收益的最大目標。電網的收益模型為 (7) 式中:p*為電網購電價的平均值;pDG_loss為該時間段內的網損;ρ為電網公司能接納的能源服務商并網電量。 圖3 2層博弈模型 2.3.2 電力系統約束 (1) 電壓約束 Umin≤|Ui|≤Umax (8) 式中:Umin和Umax分別為i節點的電壓上下限。 (9) 式中:Vtotal為所有節點的電壓穩定因子的加和,用來表示整個系統的電壓穩定情況,值越小說明系統越不穩定。 (2) 分布式能源的最大滲透率 (10) (11) 式中:PD和QD為i節點負荷的有功功率和無功功率;PL0和QL0為在沒有接入分布式電源之前的系統總的有功網損和無功網損。 本文以修改的IEEE-39節點電力系統的數據來分析上述2個博弈模型,測試系統見圖4(圖中數字表示節點,表示發電機,表示風力發電)。 圖4 IEEE-39節點電力系統 第1層:假設某時刻電網公司和能源商群體進行談判交易,并且交易電量滿足系統的安全可靠性要求且電網公司和能源服務商群體的估價和對彼此的出價推斷都服從均勻分布,雙方估價分別為vb~U(0.72,0.77)和vs~U(0.73,0.78),其中vb=0.75,vs=0.756;雙方的出價分別為ps~U(0.71,0.76)和pb~U(0.73,0.765),則博弈交易結果見表2。 由表2可見,由于第1輪報價不滿足貝葉斯納什均衡條件,故進入第2輪的談判,根據公式計算出第2輪的報價滿足pb≥ps,交易成功。故根據定義和政策,則能源服務商個體的報價策略需在[0.752 1,1]之間。 表2 均勻概率分布的談判結果 第2層:假設該時段電網允許1 000 MW分布式能源并網,且能源服務商A和B分別處于節點37和34附近,配備有自建的風電機組和自備儲能裝置,而且能源服務商A和B的報價是已知的,分別為0.76和0.77。由式(8)~(13)可知,該模型必須在滿足式(12)的情況下使式(13)獲取最大值,即 (12) y=max{ρApA+ρBpB- (PA_Loss+PB_Loss)·p*} (13) 采用Matpower軟件中IEEE-39節點系統驗證上述模型和算法的正確性,功率基準值為100 MVA,測試了能源服務商A和B的各種策略組合得出系統總網損和電網總收益的對應關系(見圖5),并選擇3組方案進行具體比較。 圖5 電網總收益與系統總網損的關系圖 表3 3種規劃方案 由表3可知,方案2相較于方案1電網收益更高、并網總量更多,并且系統總網損較低;方案2相較于方案3在電網收益相差不多的情況下,系統網損較低。因此,方案2優于其他2個方案。由圖5可知,在本文的模型下,電網收益與系統網損開始是成正比關系,隨后達到頂峰,但是需要考慮系統網損的限制,系統網損過大,也不建議實施對應的策略。 隨著售電側改革的推進,需求側用戶的博弈行為發生了質的變化,自建分布式能源的用戶可以以售電主體的身份向電網公司或售電公司進行售電。本文介紹了能源服務商群體和電網公司之間的博弈模型以及能源服務商個體之間的博弈模型。通過第1層模型可以采用拍賣競價的方式得出以能源服務商為收益對象的售電價區間。第2層模型在第1層模型得出的價格區間內,能源服務商個體之間進行博弈,以電網為收益對象,得出在電網收益最優和電力系統安全穩定的基礎下的分布式能源并網的策略方案。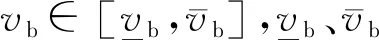
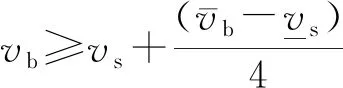

2.3 能源服務商個體間的博弈模型
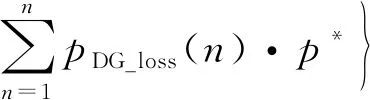
3 算例分析
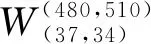
4 結 語

