高斯偽譜法在變推力導彈彈道優化中的應用*

李怡昕，李旭，劉少波，康鵬

(北京電子工程總體研究所，北京 100854)

0 引言

推力可調固體火箭發動機可根據作戰任務、作戰平臺實時調節推力大小，實現推進劑能量的合理分配，從而實現武器裝備作戰能力多樣化，因而成為固體火箭發動機發展的趨勢[1]。

國外已在推力可控固體火箭發動機的應用方面取得一些進展。美國Aerojet公司的EIHAWK導彈集成了喉栓式推力可調噴管，在裝藥量一定的條件下成功實現導彈增程。美陸軍精確攻擊導彈PAM采用了Aerojet公司的喉栓式變推力發動機，可根據任務目標實時調節推力，從而擴大作戰范圍，且在2007～2009年間，成功進行多次飛行試驗，展示出固體發動機推力可調技術的可行性[2]。

近年來，國內外學者對于偽譜法用于最優控制問題的應用研究愈加廣泛，發展愈加成熟，而飛行器軌跡優化中的偽譜法應用研究是偽譜法應用最成功的領域之一。

目前，偽譜法在飛行器軌跡優化中的應用已取得相當可觀的成果。其中，Legendre偽譜法已被應用于解決運載火箭上升段軌跡快速優化問題[3]、通用航空飛行器性能優化問題[4]、航天飛機應急下降軌跡優化問題[5]、航天器最優轉移軌道問題[6]、月球軟著陸軌跡快速優化問題[7]；Gauss偽譜法已被應用于解決小推力航天器軌跡優化問題和Delta運載火箭上升段軌跡優化問題[8]、日-火Halo轉移軌道快速優化設計問題[9]、多級固體運載火箭上升段軌跡快速優化問題[10]、空空導彈最優中制導律設計中的應用問題[11]；月球軟著陸軌道優化中的應用問題[12]、高超聲速飛行器的軌跡優化問題[13]。總的來說，國內外對于偽譜法在飛行器軌跡優化設計中的應用正處于快速發展向逐步成熟的邁進階段[14]。

針對攔截近程目標，本文采用變推力控制，選用固體火箭發動機實現推力可調，提出考慮末速最大的目標函數，給出相應的約束條件，并使用高斯偽譜法進行彈道優化設計，最后給出相應的仿真校驗結果。其中，選用的變推力固體火箭發動機推進劑質量給定，可根據實際需要調節推力大小。本文將高斯偽譜法應用于處理可變推力近程導彈彈道優化設計，在推進劑一定的條件下考慮合理分配能量，提出了一種設計變推力彈道的新思路。

1 建立高斯偽譜優化模型

1.1 導彈運動學模型

本文作如下假設：導彈在整個飛行期間都處于瞬時平衡狀態；導彈繞彈體軸的轉動是無慣性的；導彈的控制系統理想工作，無誤差，無時間延遲。

導彈在鉛垂平面內的運動方程組可以簡化為

(1)

式中：m為導彈質量；v為速度；FY為升力；FX為阻力；G為重力；P為推力；α為攻角；θ為彈道傾角;重力加速度g=9.81 m/s2。

改寫成狀態方程的形式

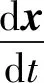
(2)

式中：狀態變量x=(v,θ,x,y,m)T；控制變量u=(P,α)T；t0為初始時刻；tf為末端時刻。

1.2 基于高斯偽譜法的離散表示

Gauss偽譜法實質上是一種離散變量表示法，其核心在于將狀態變量和控制變量在高斯點上離散，并以離散點為節點構造Lagrange插值多項式逼近原連續函數。下面將利用高斯偽譜法完成系統微分方程式(2)到代數方程式(11)的轉化[15]：

首先，將原系統的狀態方程式(2)做時域變換

(3)

將原時間區間t∈[t0,tf]映射到τ∈[-1,1]，則變換后的最優控制問題狀態方程為

(4)

性能指標、邊界條件、不等式約束為

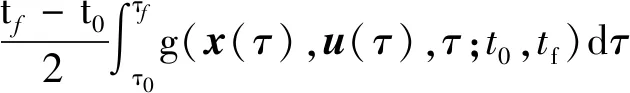
(5)

Φ(x(τ0),t0,x(τf),tf)=0,

(6)

C(x(τ),u(τ),τ;t0,tf)≤0,τ∈[-1,1],

(7)

式中：容許控制u(τ)∈U;τ∈[-1,1]。

其次，在區間τ∈[-1,1)內選取Gauss點τk(k=1,2,…,N)作為節點構造Lagrange多項式逼近原連續狀態變量x(τ)和控制變量u(τ)，即離散化為

(8)

(9)

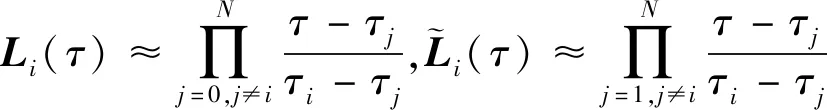
記Xk=X(τk)=x(τk)，Uk=U(τk)=u(τk)。式(8)對時間求導則有

(10)

式中：D∈RN∧(N+1)為微分矩陣，從而系統微分方程式(2)轉化為代數約束：

(11)

式中：k=1,2,…,N。

原性能指標、邊界條件和不等式約束式(5)到式(7)可離散表示為

(12)

Φ(X0,t0,Xf,tf)=0,

(13)

C(Xk,Uk,τk;t0,tf)≤0,

(14)

式中：ωk為高斯權重系數;k=1,2,…,N。

至此，原最優控制問題最終轉化為非線性規劃問題，式(11)到式(14)定義的非線性規劃問題的解就是原最優控制問題的近似解[16]。轉換所得NLP問題采用序列二次規劃(SQP)方法求解。

2 彈道優化方案設計

本文以近距導彈攔截目標為特定研究背景，在推進劑質量給定的情況下采用Gauss偽譜法進行彈道優化設計，考慮選取J=vf末速最大為優化目標函數，旨在提高其末端過載能力。

2.1 發動機方案

為了進一步驗證推力可調的彈道性能，本節給出變推力發動機的主要參數，且將在此基礎上用高斯偽譜法進行彈道優化設計并與傳統推力形式的彈道作比較和分析。

給出某變推力發動機參數見表1，推力調節范圍500 N～15 kN。

可控推力固體火箭發動機的技術途徑包括調節噴管喉部面積、實時改變推進劑燃速、加質發動機、膠狀推進劑發動機等，其中喉部面積可調的方案理論和試驗基礎好，能夠實現推力大小無級調節[1]。

2.2 優化模型

狀態方程(2)中，狀態變量x=(v,θ,x,y,m)T、控制變量u=(P,α)T為未知量，即需按一定的制導規律生成制導指令。即原運動方程聯立控制方程則方程組封閉，給出相應的初始條件即可求解。

本節提出一種高斯偽譜法的優化模型，以J=vf最大為目標函數，約束條件為攻角約束-40°≤α≤40°和法向過載約束-60≤ny≤60，選取u=(P)作為待優化控制變量，由比例導引給出α值。

比例導引給出α值的原理如下：

第1步：由比例導引

(15)

給出N個高斯點τk(k=1,2,…,N)上的過載指令；

第2步：根據預先設定的狀態變量、控制變量猜測區間將狀態變量、控制變量在各高斯點τk(k=1,2,…,N)上初始化，即此時各高斯點上x=(v,θ,x,y,m)T，u=(P)為一系列確定值；

第3步：由動力學方程

ny=

(16)

得出各高斯點上的一系列α值。

隨著高斯偽譜法優化的逐步進行，α值同步更新，該最優控制問題可以求解。

3 仿真校驗

導彈初始狀態x0=0，y0=10 km，v0=400 m/s，滿載質量mfull=82.3 kg，空載質量memp=55 kg。

仿真圖中*號各點為高斯偽譜法優化得到的離散狀態量/控制量，另將高斯偽譜法得到的P，α作為輸入進行數值積分，其結果用細實線表示，以驗證高斯偽譜法優化結果的正確性。

3.1 發動機方案對比

目標設定為(xt,yt)=(5,12) km定點目標，導彈發射角θ=90°。

首先在表1給出的發動機參數的基礎上，給定幾組工程常用推力比，通過仿真計算其在比例導引下的彈道，并比較末速如表2所示，仿真結果見圖1。

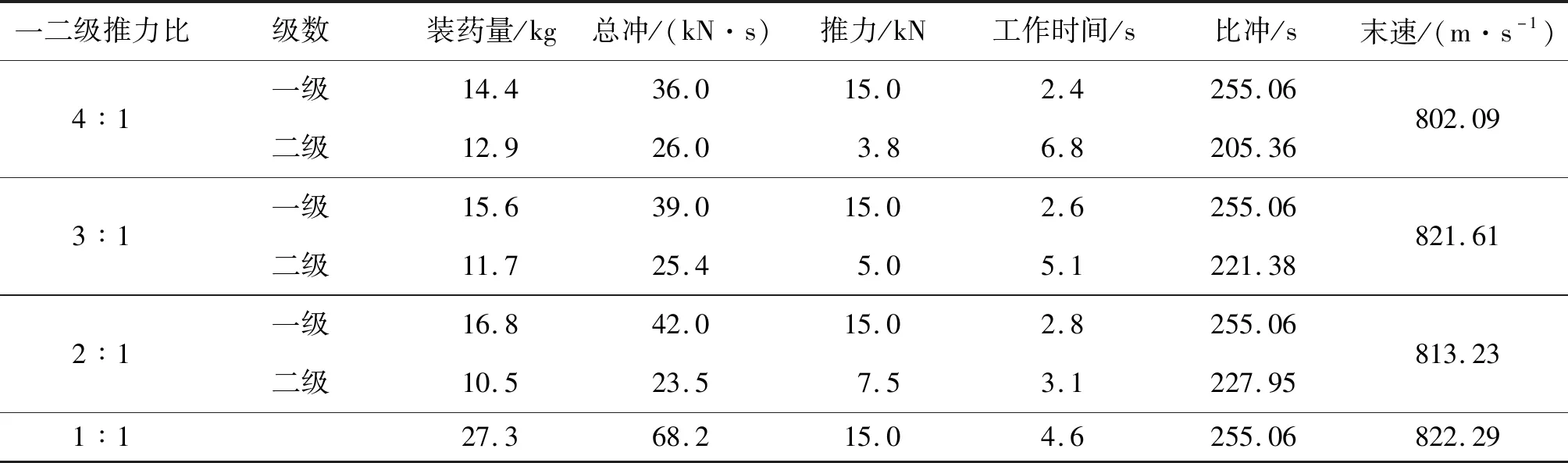
表2 傳統發動機參數Table 2 Parameters of traditional engines

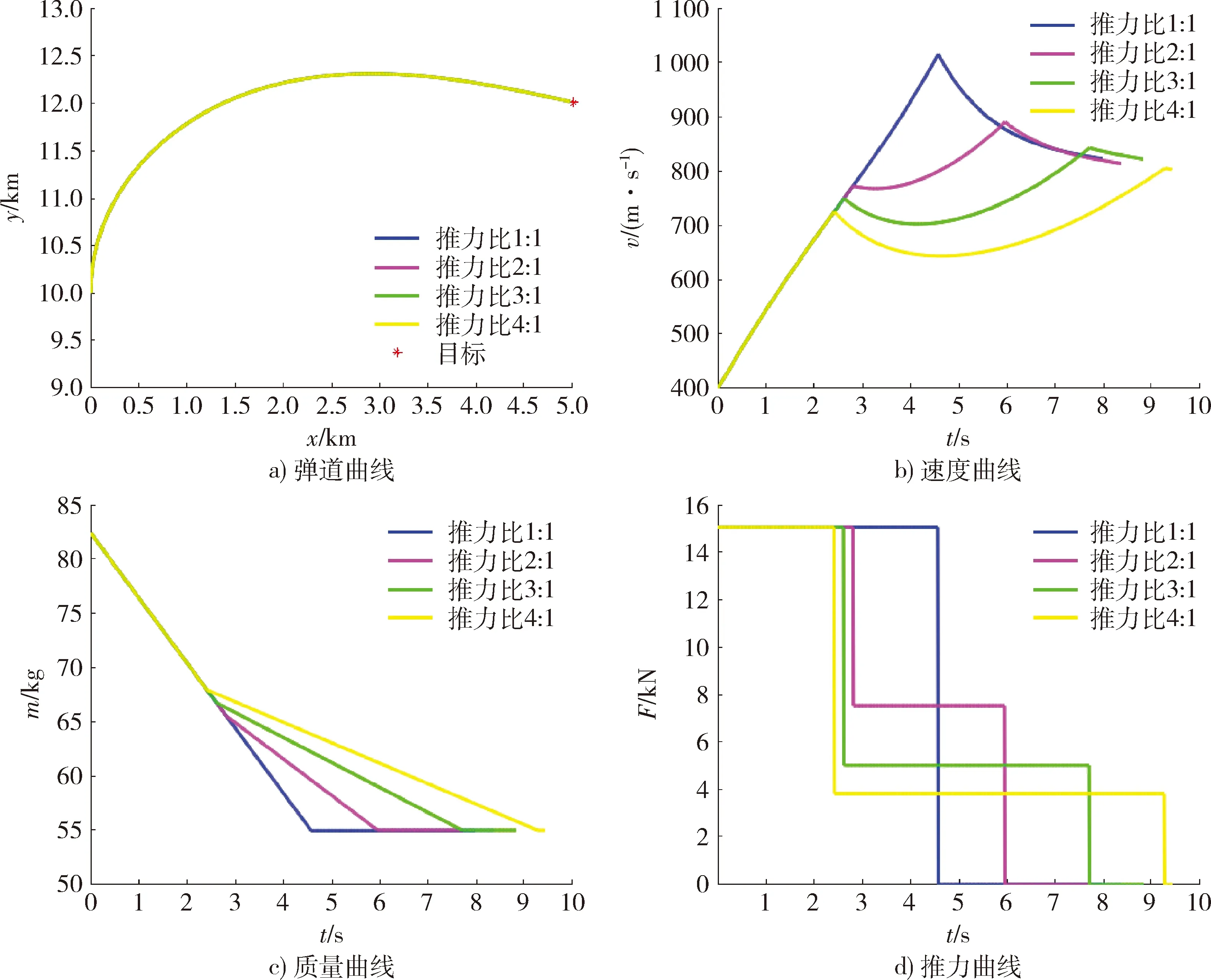
圖1 傳統發動機方案的彈道仿真Fig.1 Trajectory simulation of traditional engine schemes

由表2可知，近距目標考察末速最大時推力比1∶1性能最優(末速最大)，將其與高斯偽譜法優化所得的變推力方案作對比，給出仿真結果如圖2所示。

分析仿真結果可知，對比最佳的傳統發動機方案比例導引彈道，推力可調的發動機方案下，以末速最大為優化目標，高斯偽譜法優化得到的彈道末速提升9.97%，表明采用變推力控制可顯著提升導彈的彈道性能，對比結果見表3。

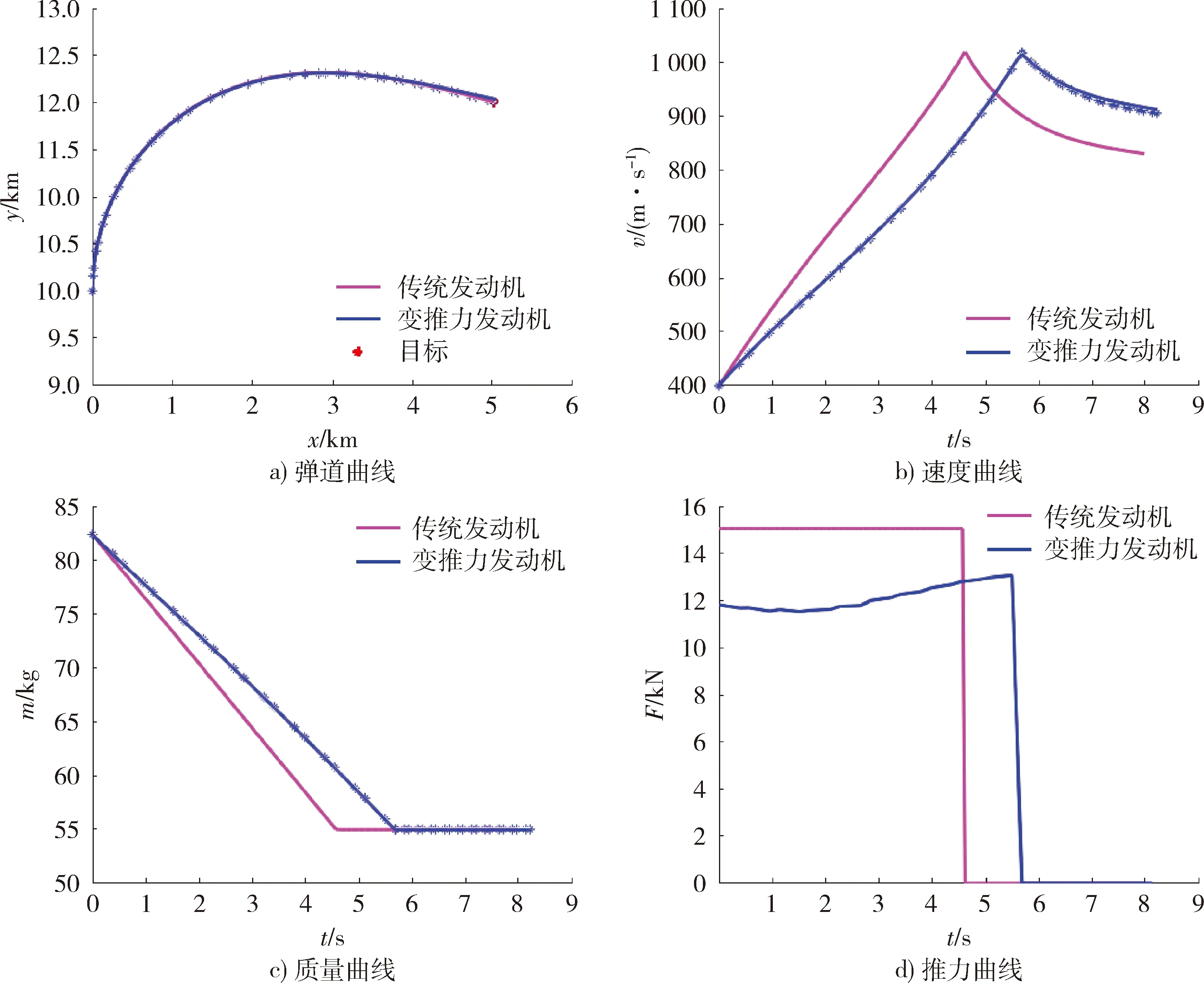
圖2 兩種發動機方案的彈道仿真Fig.2 Trajectory simulation of two engine schemes

表3 2種發動機方案的性能Table 3 Trajectory performance comparison of two engine schemes

由圖2可看出，高斯偽譜法優化結果與數值積分結果有一定誤差，這是由于高斯偽譜法給出的最優解為離散值，由式(9)可知，最優控制變量應以這些離散點作為節點構造Lagrange插值多項式來逼近。而細實線表示的曲線則是在離散推力值的基礎上線性插值作為輸入量進行數值積分的結果，因此在推力值波動較大時，二者出現誤差。

3.2 有效性驗證

為進一步驗證高斯偽譜法應用于可變推力導彈彈道優化的有效性，本節考慮近程導彈全向發射情況，選用比例導引控制變量u=(P)的高斯偽譜法優化方案，在表1給出的推力可調發動機參數的基礎上進行彈道仿真。

目標設定為(xt,yt)=(5,12) km定點目標，選取導彈發射角θ=0°,30°,…,150°，同3.1節給出推力可調與最優傳統推力的彈道性能對比結果見表4。

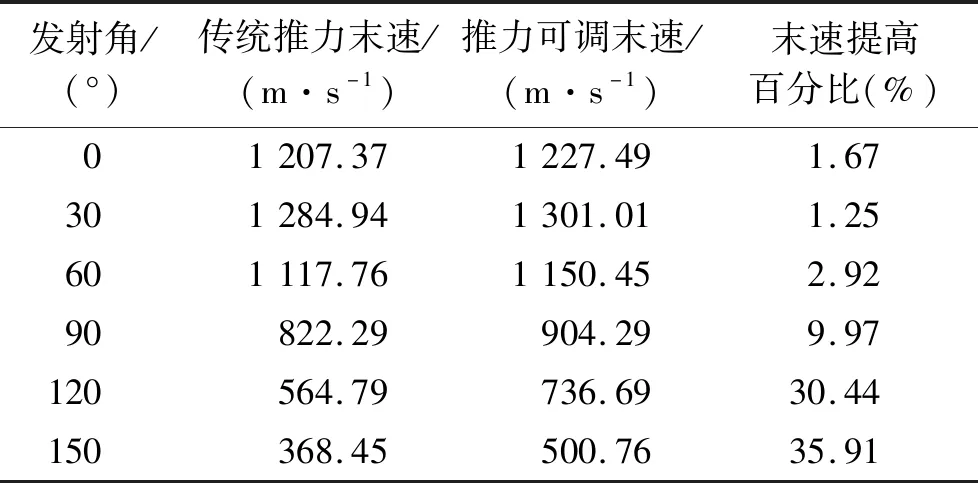
表4 全向發射兩種發動機方案的性能Table 4 Trajectory performance comparison of two omnidirectional attack engine schemes

高斯偽譜法給出導彈在不同的發射角θ=0°,30°,…,150°下的變推力彈道優化結果如圖3所示，高斯偽譜法優化得到的彈道末速分別提升1.67%，1.25%，2.92%，9.97%，30.44%，35.91%。區別于傳統推力方案，圖3d)推力曲線圖體現出可變推力控制下的推力形式多樣性，說明了高斯偽譜法應用于可變推力導彈彈道優化設計的可行性和有效性。

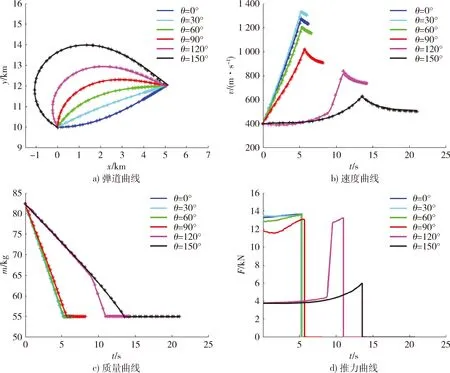
圖3 全向攻擊彈道仿真Fig.3 Trajectory simulation of omnidirectional attack

4 結束語

對于可變推力導彈彈道優化問題，本文提出基于比例導引的變推力導彈彈道優化模型，研究在推進劑質量給定的條件下進行能量的合理分配。仿真結果表明了高斯偽譜法應用于可變推力導彈彈道優化設計的有效性。本文采用比例導引給出制導指令，總體計算量小，可以實時在線運行。后續將對打擊中遠程目標及機動目標的情況進行研究，同時考慮采用hp-自適應方法對其進行改進，逐步細化網格并提高基函數階次以獲得更高的精度。