聚類分析和支持向量機回歸的交通流預測

鄧晶 　張倩

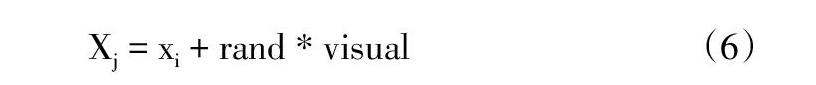
中文摘要：本文以交通流數據為研究對象，主要對數據挖掘技術在交通流預測方面的應用進行了研究和探討。并基于研究內容，提出了基于聚類分析和支持向量機回歸的交通流預測模型。并針對支持向量機參數選擇，提出了人工魚群算法使其快速尋找到最優參數組合。最后，通過實驗數據論證本文所提出的算法和模型。

關鍵詞：數據挖掘;交通流預測;聚類分析;支持向量機;人工魚群算法

中圖分類號：TP18 ? ? ? ?文獻標識碼：A

文章編號：1009-3044（2019）15-0013-04

Abstract： This paper takes traffic flow data as the research object， mainly studies and discusses the application of data mining technology in traffic flow prediction. Based on the research content， a traffic forecasting model based on clustering analysis and support vector machine regression is proposed. Aiming at the parameter selection of support vector machine， an artificial fish swarm algorithm is proposed to quickly find the optimal parameter combination. Finally， the algorithm and model proposed in this paper are demonstrated by experimental data.

Key words： data mining; Traffic flow forecasting; cluster analysis; Support Vector Machine; afsa

隨著城市規模和交通出行需求的不斷增長，人們對出行決策服務的需求越來越強烈。如何能夠實時準確地預測交通流成為交通管理和控制是否能有效實現的關鍵問題。傳統的交通流預測模型早已無法滿足實踐中高實時性、高精度的預測要求。目前，在智能交通流預測領域，主要采用基于非線性理論的預測模型、基于神經網絡的預測模型、基于支持向量機的預測模型和多模型融合的預測模型等，以研究、開發和實現實時道路交通預測。支持向量機（SVM）是近十幾年出現的一種先進的數據挖掘方法。由于交通流數據具有數據量大、維度高、非線性等特征，SVM采用結構風險最小化的學習方式可以實現在小樣本的學習環境下，采用凸優化的學習方式，有效地避免過擬合和局部最優，從而使交通流預測性能大大提高。對于樣本量較大的交通流數據，按照不同的屬性對數據進行聚類分析，同一類別內的數據相似度更高，且數據樣本量相對減小，使用支持向量機回歸進行預測能夠獲得更好的預測效果。最后的實驗數據也證明了這一點。

1 數據預處理

交通數據采集的途徑和方法有很多。在采集過程中不可避免的會產生一些問題。假如不對原始采集數據進行預處理，檢查并清除問題數據，妥善處理好缺失值和異常值，必然會使研究結果產生很大偏差。

本文采用牛頓插值法對缺失數據進行補值計算。采用合適的小波函數對數據進行一定尺度的小波變換，通過信號重構，去掉噪聲數據。考慮到交通數據的特點，采用0均值標準化對數據進行歸一化處理。

最后，從大量的交通流原始數據中選擇出特征集。數據特征選擇是從已知的特征集合中選擇一個子集，該子集可以全面有效地對數據進行描述，后續的預測分析工作可以針對該子集進行。選擇出優良的特征數據，不僅可以降低數據計算量，提升效率，而且可以幫助研究者更深入的理解研究對象。

2 基于聚類分析和支持向量機回歸的交通流預測

交通流數據具有非線性、高維度的特性。支持向量機回歸算法在處理小樣本、非線性、高維度數據時，具有很好的預測效果。因此，我們采用支持向量機作為核心預測算法。但交通流數據樣本數量比較龐大，可能會導致支持向量機的訓練速度緩慢，且預測容易產生偏差。針對這一問題，我們首先采用K-means++聚類算法將數據按照交通流量、天氣、節假日等屬性進行聚類得到若干類別。同一類別內的數據相似度高，數據規模也相對較小。然后，通過實時數據匹配相應類的數據進行樣本訓練，再使用支持向量機進行預測能夠獲得更好的預測效果。

在支持向量機模型參數的選擇的問題上，采用人工魚群算法對支持向量機回歸的參數進行優化，采用合適的參數能夠進一步提高預測精度和推廣能力。

2.1交通流數據的聚類分析

傳統的K-means聚類算法需要人為確定初始聚類中心。不同的聚類中心可能會導致不同的聚類結果。在交通流數據聚類分析中，我們采用K-means++聚類算法，它的核心思想是選擇的初始聚類中心之間的距離要盡可能遠。

2.3人工魚群算法優化支持向量機參數

支持向量機回歸中參數的選擇對模型的預測效果有著十分重要的影響。即損失函數ε、懲罰因子C、高斯徑向基函數。如何組合這三個參數成了支持向量機回歸不可避免的問題。由于參數選擇的復雜性，目前還沒有確定的理論來指導，而群體智能算法在參數優化問題上有很好的效果。本文使用群體智能化算法中的人工魚群算法對支持向量機的參數進行尋優。人工魚群算法對初值和參數不太敏感，具有自適應搜索空間的能力，且魯棒性強，收斂速度快。更重要的是，能夠避免陷入局部極值而失去全局最優。

在人工魚群算法中包括三種主要的算子：聚群算子、追尾算子和覓食算子。這三種算子是算法的核心，并且決定算法的性能和最優解搜索的準確度。

設Xi表示第i條人工魚的位置;Yi表示第i條人工魚的適應度值。其中，Yi=f（Xi）;β表示擁擠度因子;try表示人工魚在覓食算子中的最大試探次數。

（1） 覓食算子

人工魚按式（6）隨機選擇當前感知范圍內的一個位置Xj，若Yi〉Yj，則按式（7）向該位置前進一步，達到一個新位置Xnext。反之，則重新隨機選擇位置，判斷是否滿足前進條件;這樣反復嘗試try次后，如仍不能滿足前進條件，則在感知范圍內隨機移動一步。

Xj = xi + rand * visual ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （6）

Xnext = Xi + rand * step * ? ? ? ? ? ? ? ? ? ? ?（7）

（2） 聚群算子

人工魚i以自身位置Xi為中心，其感知范圍內的人工魚數目為nf，當nf ≥1時，這些人工魚形成如式（8）的集合Si，按式（9）計算Si的中心位置Xcenter。如果Yenter< Yi且Ycenter/nf>β*Yi，表明伙伴中心有很多食物且不太擁擠，則按式（10）朝該中心方向移動一步;否則，執行覓食算子。

Si = { xj∣〡xj - xi〡≤ visual } ? ? ? ? ? ? ? ? ? ? ?（8）

Xcenter = ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（9）

Xnext = xi + rand * step * ? ? ? ? ? ? ? ? ? （10）

（3） 追尾算子

人工魚i根據當前位置搜索其感知范圍內所有伙伴中適應度最小的伙伴位置Xmin，其適應度為Ymin，如果Ymin< Yi，就Xmin為中心搜索其感知范圍內的人工魚。數目為nf，且Ymin< Yi且Ymin/nf>β*Yi，表明該位置較優且不太擁擠，則按式（11）向著適應度最小伙伴位置Xmin的方向前進一步。否則，執行覓食算子。

Xnext = xi + rand * step * ? ? ? ? ? ? ? ? ? ? ? ? ? ?（11）

人工魚群算法中每條人工魚首先分別試探執行聚群算子和追尾算子，通過目標函數計算其適應度是否得到改善。將適應度改善較大的算子作為該條人工魚的更新算子;否則執行覓食算子;若這條人工魚達到覓食算子的最大嘗試次數后，適應度依舊沒有改變，則在自己周圍隨機移動一個位置。所有人工魚執行上述操作后，最終人工魚群集結在幾個局部最優解周圍，且全局最優極值區域周圍也有較多人工魚集結。

該模型的詳細描述如下：

Step1：設置支持向量機回歸相關參數的取值范圍：包括損失函數ε、懲罰因子C、高斯徑向基函數δ。對人工魚群算法進行參數設置。包括魚群的種群規模，種群迭代次數，種群的擁擠度因子，最多試探次數，人工魚的感知距離以及人工魚移動的步長等;

Step2：在聚類分析后得到的數據集中，選取部分測試數據，剩下的數據作為訓練數據集用來進行SVR的預測分析，從而判別SVR的預測效果;

Step3：人工魚群中的每條魚是SVR優化參數組合（ε、C、δ），即損失函數、懲罰因子、高斯徑向基函數。根據setp1中的參數取值范圍初始化魚群位置。對所有人工魚并行尋優;

Step4：根據SVR運用訓練數據集得到的預測結果，通過計算預測值與實際值的均方根誤差，以此作為人工魚的目標值。同時，比較每條人工魚目標值的大小，將其中的最小值作為當前魚群中的最優，并保存當前的最優人工魚參數組合（ε、C、δ）;

Step5：每條人工魚分別模擬聚群行為和追尾行為，通過選擇游動后目標值比較小的行為來確定實際執行的行為。覓食行為是缺省行為;

Step6：在魚群中，每更新一次位置，都需要計算當前魚群的最優目標值。如果其中一條魚對應的目標值小于目前保存的最優目標值，那么將其替代保存的最優目標值，同時保存最優人工魚參數組合（ε、C、δ）。否則，最優目標值和參數組合保持不變;

Step7：判斷迭代次數是否達到最大迭代次數。如果達到，輸出人工魚參數組合（ε、C、δ）和最優目標值。否則，返回step5。

2.4基于K-means++聚類算法和支持向量機回歸交通流預測

本文研究的交通流數據包括交通流量、車速、占有率、日期、天氣、交通時間等，在分析各方面因素后，設計了一種基于基于K-means++聚類算法和支持向量機回歸的交通流預測模型。該模型的預測流程為：

Step1：對數據進行預處理，得到相對完整準確的交通流特征數據;

Step2：將交通流特征數據按照交通流量、天氣、節假日等屬性進行聚類得到若干類別，使得同一類別內的數據相似度更高，每個類別數據的規模也相對小;

Step3：計算交通流實時數據與已經生成的所有聚類簇的歐氏距離，匹配到相應的簇中，使得簇內的數據與預測當天的特征相似度更高。將該簇內的交通流數據作為訓練樣本;

Step4：使用選取的訓練樣本數據，應用人工魚群算法對支持向量機參數尋優，得到支持向量機最優參數組合;

Step5：使用參數優化后的支持向量機回歸模型進行預測，得出預測結果;

3實驗結果和分析

3.1數據來源與評價指標

本文實驗數據來源于美國加州交通局的PEMS系統。PEMS系統的數據是開源的，用于各類研究者學習和使用。在PEMS系統中，我們隨機選取一個時段的數據。該段數據已經被處理成5分鐘一個間隔的交通流數據。包括車輛流數、車速及車道占有率等。另外，引入天氣因子，對天氣情況特征做出說明;引入時間類別，對普通工作日、節假日、重大節日等作出區分。

針對本文的最終目的是為了準確地進行回歸預測，我們引入了廣泛應用于回歸問題的評價指標，分別為平均絕對百分比誤差（MAPE）和均方跟誤差（RMSE）。其中，MAPE表征了預測值偏離實際值的程度。MAPE越小，表明預測值越接近于實際值，預測效果越好。RMSE表征了誤差大小以及誤差分布的離散程度。RMSE越小，誤差離散程度就越低，預測效果也就越好。

3.2 實驗一：基于聚類分析和支持向量機回歸的交通流預測

3.2.1 聚類分析

本文抽取了2017年12月的交通流數據進行聚類分析。12月一共有31天，將其中的2日、11日、18日的交通流數據抽出，作為測試樣本進行驗證。剩下的28天數據進行聚類分析。根據最佳聚類數計算方法，即聚類數應該在2到之間。為數據樣本數28。則最佳聚類數取值為2到5之間。對12月份28天交通流量歷史數據進行聚類，采用輪廓系數來評價聚類效果，不同K值對應的聚類結果和輪廓系數的實驗數據如表1。

由上表可知，當K=4時，聚類效果最好。即最佳聚類數K為4，聚類結果為四個簇。第一類為圣誕節及連接的周末;第二類是周末;第三類是工作日且天氣良好;第四類為普通工作日且天氣狀況差。由此可見，聚類后的每個類的特征都比較相似，類間特征差別比較明顯。之后將預測的日期匹配到相應的聚類簇中，使用簇內數據作為訓練樣本，得到更好的預測效果。

3.2.2 支持向量機交通流預測

本文對2日、11日、18日部分時段進行交通流預測。計算預測時段前三個小時的交通流量數據與四個簇類樣本中心的歐式距離，得到某一個聚類簇的歐式距離最小，并將其歸為一類。將這一簇內的數據作為訓練樣本數據集

以下以11日的預測為例，說明實驗結果。

當預測11日的交通流量時，計算得到與第三個聚類的歐式距離最小。選取第三個類中14天的數據為訓練樣本。使用人工魚群算法計算得到最優參數組合（ε、C、δ）=（0.74、69、0.26）。使用優化的參數組合建立預測模型得到預測結果。與傳統的SVR預測結果和實際值的對比如圖1。

為了驗證本文提出的預測算法，將其與傳統的支持向量機回歸算法、ARIMA預測算法、BP神經網絡預測算法進行對比。在相同的實驗環境下，不同算法的MAPE和RMSE指標如表2。

3.2.3 實驗結果分析

由圖1可以看出，基于聚類分析和支持向量機回歸預測模型要優于傳統的支持向量機模型。其預測曲線與原始實際值擬合的更好，變化趨勢也與原始實際值基本一致。這表明本文提出的預測模型使用聚類對數據區分后進行訓練，并對參數進行優化，可以有效地削弱隨機數據導致的誤差，從而有助于提升短期交通流預測的準確性。

由表2可以看出，ARIMA算法預測精度最差。傳統的支持向量機和BP神經網絡算法兩項指標比較接近，預測精度基本相似。但支持向量機還是略勝一籌。兩種SVR預測模型都優于兩種經典的預測算法。而基于聚類分析和支持向量機回歸預測模型的兩項指標又優于傳統的SVR。其中MAPE降低了30.2%，RMSE降低了35.7%。

4 結束語

本文在對交通流數據進行預處理后，通過聚類分析和支持向量機回歸算法建立預測模型，實現對非線性、高唯度交通流數據的有效預測。經實驗驗證，優于傳統的預測模型且更接近于實際交通流數據。

由于時間和水平有限，本文的研究內容有待于進一步拓展。主要有以下幾點：

由于影響交通流的因素很多，本文只考慮了其中重要的若干因素，需要考慮將更多的影響因子加入模型中。

人工魚群算法對SVR參數尋優收斂速度較慢，可以研究其與其他尋優算法結合，以達到更好的參數優化效果。

參考文獻：

[1] 李青. 城市交通流預測關鍵技術研究[D]. 西南科技大學， 2015.

[2]王允森，蓋榮麗，孫一蘭. 基于牛頓迭代法的NURBS曲線插補算法[J].組合機床與自動化加工技術，2013（4）：13-17.

[3]丁世飛，齊炳娟，譚紅艷.支持向量機理論與算法研究綜述[J].電子科技大學學報，2011，40（1）：1-28.

[4] Son J，Jung I，Park K，et al . Tracking-by-Segmentation with Online Gradient boosting decision Tree[C]. IEEE Internatiomal Conference on Computer Vision .IEEE，2015： 3056-3064.

[5] Arthur D，Vassilvitskii S. k-means++：the advantages of careful seeding[C]Eighteenth Acm-Siam Symposium on Discrete Algorithms. Society for Industrial and Applied Mathematics，2007：1027-1035.

[6] EI-Sheimy N， Nassar S， Noureldin A . Wavelet de-noising for IMU alignment[J].IEEE Aerospace & Electronic System Magazine，2004，19（10）：32-39.

[7]朱連江，馬炳先，趙學泉. 基于輪廓系數的聚類有效性分析[J]. 計算機應用，2010（s2）：139-141.

[8] 李曉磊，薛云燦，路飛，等. 基于人工魚群算法的參數估計方法[J]. 山東大學學報（工學版），2014，34（3）：84-87.

[9] Yao X ， Wang X， Zhang Y. Summary of feature selection algorithms [C]. International Conference on Advances in Multimedia Modeling. Spring-Verlag， 2012：452-462.

[10]譚滿春，馮牽斌，徐建閩. 基于ARIMA與人工神經網絡組合模型的交通流預測[J]. 中國公路學報，2007，20（4）：118-121.

【通聯編輯：唐一東】