基于伯努利效應在煤塵檢測通道的實現研究

景明明 韓東志

摘要：依據流體力學中的伯努利效應，優化現有裝置，從而設計了具有效應段的煤塵濃度檢測通道裝置。采用CFD軟件，在Gambit2.4中建立改進裝置模型，在Fluent6.3設定計算求解參數，通過對仿真結果的云圖分析、數值分析以及不同管道的粒子參數對比分析，得出了伯努利效應在改進裝置中的有效性。經過與項目組之前研究的文丘里效應管進行速度對比以及歸一化處理，其平均速度提高了9.2%。對于后續設計煤塵濃度檢測結構具有一定的參考意義。

Abstract： According to Bernoulli effect in hydrodynamics， the existing device is optimized， and a dust concentration detection channel device with effect section is designed. Using CFD software， an improved device model is established in Gambit 2.4. The parameters of calculation and solution are set in Fluent 6.3. The effectiveness of the Bernoulli effect in the improved device is obtained through the cloud image analysis， numerical analysis and the comparison of particle parameters of different pipes. The average velocity of Venturi effect tube was increased by 9.2 times after comparing and normalizing with the Venturi effect tube studied by the project team. It has certain reference significance for the follow-up design of coal dust concentration detection structure.

關鍵詞：伯努利效應;小粒徑煤塵;速度對比;建模仿真

Key words： Bernoulli effect;small particle size coal dust;velocity comparison;modeling and simulation

中圖分類號：TP391.7 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：1006-4311（2019）09-0087-03

0 ?引言

煤礦生產的整個環節較為復雜，在生產中的每一個環節都會產生大量煤塵，嚴重影響著井下工人的身體健康，煤塵濃度過高還會引起職業病。近年因煤塵爆炸的事故屢屢發生，對廣大礦工生命安全造成巨大威脅，也造成了巨大的經濟損失[1-3]。目前市面上有許多基于不同原理的煤塵測量方法以及測量系統，如濾膜稱重法、光散射法、靜電感應法等，為煤礦井下粉塵濃度測試提供了強有力的保障。而這些測量方法普遍存在著測量結果易受人為因素影響、測量周期相對較長、不能實現連續實時測量等缺點[3-5]。因此，有效準確地檢測礦井煤塵濃度，并且實現連續實時檢測是防治煤塵污染的重要保障，也是預防作業人員患塵肺病最主要的手段。本文基于流體力學中的伯努利效應對現有測量裝置進行改進，項目組研究伯努利效應對氣固兩相流相關作用，通過CFD軟件進行建模仿真，驗證伯努利效應對煤塵通道的有效性，為后續工作研究做好相應準備。

1 ?改進裝置模型

1.1 模型原理

伯努利效應，也稱邊界層表面效應。適用于包括氣體在內的一切流體，是流體作穩定流動時的基本現象之一，反映出流體的壓強與流速的關系，流速與壓強的關系：等高流速時，流體的流速越大，壓強越小;流體的流速越小，壓強越大。實質是流體的機械能守恒，如下式所示：

其中p為流體中某點的壓強，Pa;ρ為流體密度，kg/m3;v為流體該點的流速，m/s;g為重力加速度，m/s2;h為該點所在的高度，m;c為常數[5-12]。

1.2 改進裝置圖

依據伯努利原理，圖1為基于伯努利效應的改進裝置圖，當煤塵粒子進入測量管道中，在運動過程中會發生摩擦碰撞，如果在管道內發生伯努利效應，那么壓力的逐漸減小，將會使粒子的運動速度的增加，這對于煤塵濃度的檢測通道而言，不僅可以更加準確的檢測濃度，而且降低了設備的損耗。因此，驗證改進裝置的有效性，是極其重要的。本文依據現有裝置，設計了改進裝置管道直徑D為6cm，進口段長度d1為4cm，效應段長度d2為8cm，出口段長度d3為4cm，d為效應段最小間距，如圖1所示。

2 ?幾何模型

2.1 建立及網絡劃分

為了使實驗結果更加直觀，本次實驗將模擬為2D平面模型，故將其通道結構簡化為兩個開口。利用Gambit2.4建立改進裝置的實驗模型，選擇Quad/Tri格式作為網格化的工具，Interval Size為0.1，定義左為進口，類型為速度入口邊界，定義右為出口，類型為自由出流邊界，其他默認為管壁。以d=3cm為例，簡化流場模型如圖2所示。

2.2 計算方法

利用Fluent6.3對改進裝置的內部流場進行數值模擬。選擇壓力基隱式求解器，計算模型為歐拉模型下具有較高穩定性的k-ε模型，在標準大氣壓環境中進行，定義煤塵的物理性質，將第一相流設置為air，第二相流設置為fenchen，最后定義邊界條件。

通過上述計算方法的設置，根據研究對象為小粒徑煤塵，因此設定煤塵的粒徑分別為11μm、9μm、7μm、5μm、3μm、1μm作為研究對象，設置了含塵氣流初始速度分別為3m/s、4m/s、5m/s，可實現對不同運動速度粒子的模擬化研究，同時在每一個初始速度的對應下分別設置了效應段最小值為2.5cm、3cm、3.5cm的測量通道管。

3 ?結果分析

3.1 云圖分析

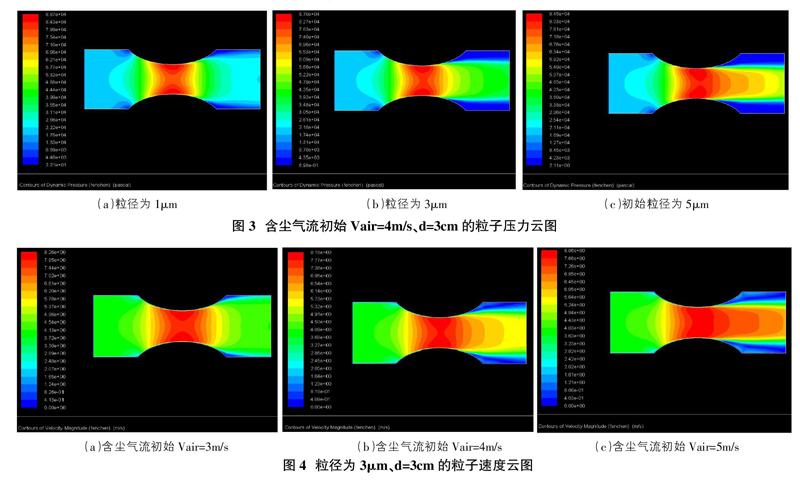
通過Fluent6.3相關求解計算，從而獲得大量的壓力云圖與速度云圖，以粒子的含塵氣流初始Vair=4m/s，d=3cm，粒徑為1μm、3μm、5μm為例。

由圖3粒子壓力云圖可知，在同等條件下，隨著粒子粒徑的增加，在管道內的效應段粒子所受壓力隨之增大，同時在效應段的壓力逐漸形成“壓力后移”現象，壓力傾向于出氣口一側。因此，對于管道而言，損耗將會隨之降低，也便于日后對設備的維護。

由圖4粒子速度云圖可知，在同等條件下，隨著粒子粒徑的增加，在管道內的效應段粒子運動速度沒有增大反而逐漸減小，同時也形成了“速度后移”的現象。雖然在效應段的粒子運動速度有所減小，但傾向于出口一側粒子運動速度較之而言略有提高，因此該現象可降低煤塵的沉降問題。

3.2 數值分析

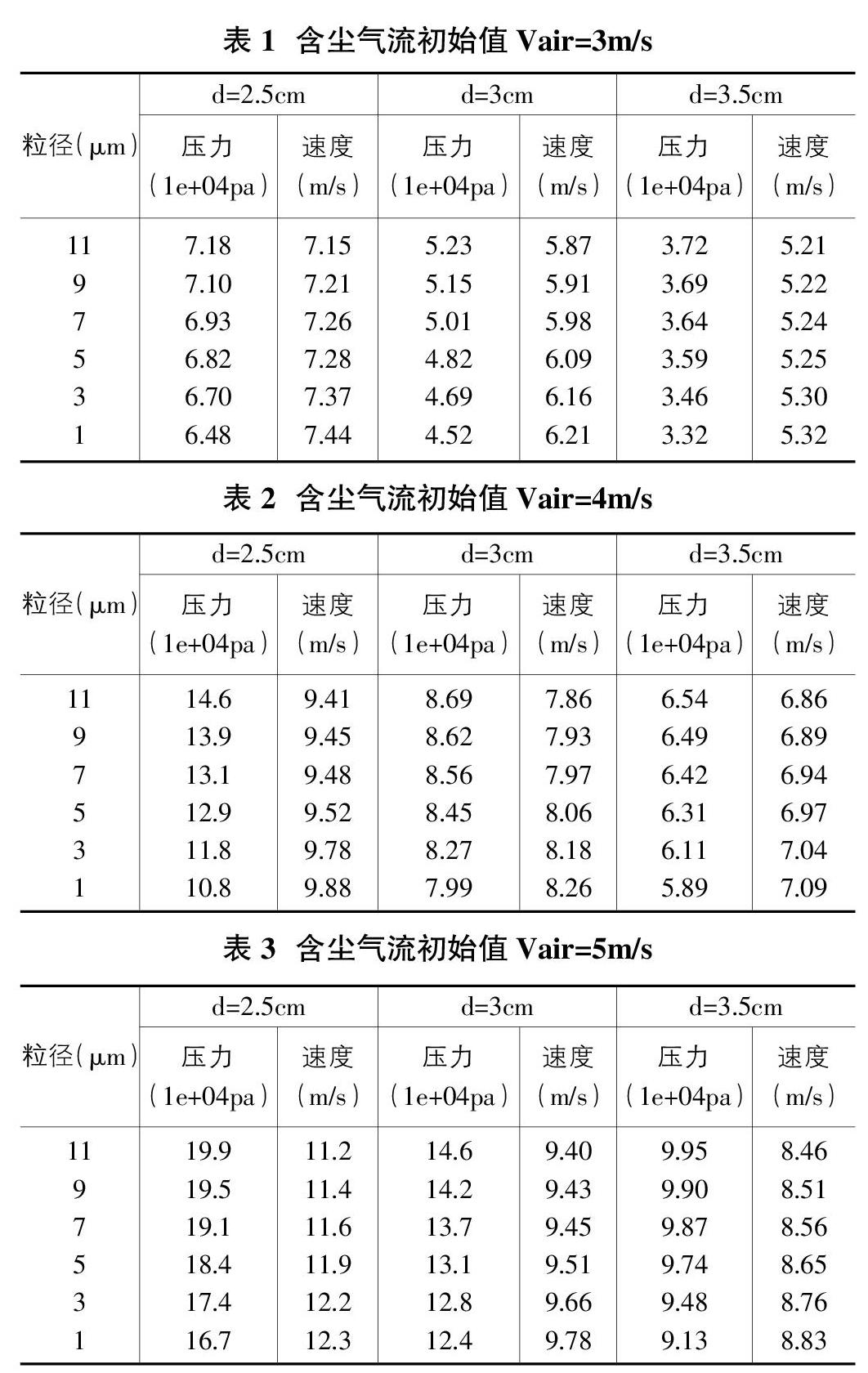
通過相應云圖，從而獲取不同狀態下的數值，分別取不同含塵氣流初始速度值作為實驗的研究前提，通過不同的顆粒物粒徑以及不同的管道效應段最小值，從而進行相關數值分析，如表1-表3所示。

由表1-表3中煤塵的壓力與速度數據，可以清晰的得出：在改進測量裝置中，無論是怎樣的實驗條件，當粒徑的逐漸減小時，壓力總是隨之減小，反而速度會逐漸增大，反之亦然，因此驗證了伯努利效應在改進裝置中的有效性。

3.3 不同管道的參數對比分析

改進裝置中伯努利效應得到充分利用，但對于是否提高了粒子的運動速度，需要作進一步分析。因此，改進裝置與項目組研究的文丘里效應管的粒子運動速度進行對比，選擇管道內效應管的最小值d=3cm，含塵氣流速度初始值Vair=4m/s，作為對比參考。由于其速度對比如表4所示，在同等實驗條件下進行模擬實驗。

根據表5可知：對于煤塵而言，改進裝置不同粒徑的運動速度均大于項目組研究的文丘里效應管，有利于提高煤塵濃度測量的準確性。對表5的速度值進行相關處理，如圖5所示。

由圖5可知：對于小粒徑煤塵，粒子在改進裝置中的平均速度提高了9.2%，因此，伯努利效應對于測量結果的準確度具有一定的提高，也保證了對煤塵的檢測精度。

4 ?結論

①首先對流體力學中的伯努利效應進行介紹，依據現有裝置的結構，優化現有裝置，從而設計了具有效應段的煤塵濃度檢測裝置，從而進行驗證伯努利效應能否作用于改進裝置。

②采用CFD軟件，基于伯努利效應的相關原理，在Gambit2.4中建立改進裝置模型，在Fluent6.3設定計算求解參數，同時仿真實驗設定煤塵的粒徑分別為11μm、9μm、7μm、5μm、3μm、1μm，設置了含塵氣流初始速度分別為3m/s、4m/s、5m/s，在每一個初始速度的前提下分別設置了效應段最小值為2.5cm、3cm、3.5cm的測量通道管，可實現對管道的參數設定提供理論依據。

③通過對仿真結果的云圖分析、數值分析以及改進前后的粒子參數對比分析，得出了伯努利效應在改進裝置中的有效性。經過與項目組之前研究的文丘里效應管進行速度對比以及歸一化處理，其平均速度提高了9.2%。后續會結合項目組研究方向，進一步研究伯努利效應對于檢測煤塵的相關問題。

參考文獻：

[1]多英全，劉垚楠，胡馨升.2009～2013年我國煤塵爆炸事故統計分析研究[J].中國安全生產科學技術，2015，11（02）：186-190.

[2]孫博.礦井煤塵濃度測量技術研究[D].長春理工大學，2014.

[3]張二強，張禮敬，陶剛等.煤塵爆炸特征和預防措施探討[J].中國安全生產科學技術，2012，8（02）：88-92.

[4]菅潔，謝建林，郭勇義.煤礦井下煤塵濃度與煤塵粒度測定分析[J].太原理工大學學報，2017，48（04）：592-597.

[5]石天娥.氣固兩相流固相速度與濃度測量[D].東北大學，2012.

[6]陸倩倩，阮健，李勝.伯努利效應引起滑閥閥芯徑向力的研究[J].中國機械工程，2017，28（19）：2332-2338.

[7]梁磊，張玲.對流干擾下的重力分異——基性巖側向分帶及礦化的主要機制[J].地質論評，2017，63（04）：869-880.

[8]劉丹丹，曹亞迪，湯春瑞，等.基于測量窗口氣鞘多相流分析的粉塵質量濃度測量裝置優化[J].煤炭學報，2017，42（07）：1906-1911.

[9]王禮平.煤礦粉塵濃度監控系統研究與實現[D].西安建筑科技大學，2018.

[10]黃技，呂鴻冠，林燦彬，等.基于Fluent的不同雷諾系數下二元圓柱繞流的研究[J].廣東海洋大學學報，2015，35（04）：81-86.

[11]白普慶.靜電式氣固兩相流固相濃度的測量研究[D].東北大學.

[12]劉丹丹，魏重宇，李德文，等.基于氣固兩相流的粉塵質量濃度測量裝置優化[J].煤炭學報，2016，41（07）：1866-1870.