服務半徑約束下城市快遞雙層配送網絡節點選址優化

杜剛誠 冉林娜

摘要：為提高快遞配送效率，基于城市快遞雙層配送網絡的構成和優勢，建立該網絡二級節點選址模型，包括末端配送站點和便民寄存點選址，其中便民寄存點選址需考慮服務半徑約束和容量限制。提出分解算法進行模型求解，其中針對便民寄存點選址采用改進的最少點覆蓋啟發式算法，針對末端配送站點選址采用k-均值聚類算法。利用算例進行模型和算法驗證，結果表明，該模型和算法能有效解決城市快遞雙層配送網絡的節點選址優化問題。

關鍵詞：物流規劃;城市快遞;雙層配送網絡;節點選址

中圖分類號：U294.1

文獻標志碼：A

Abstract：In order to improve the efficiency of express delivery， based on the structure and advantages of the double-layer distribution network of urban express delivery， a two-level node location model of the network is established， where the nodes include the terminal distribution stations and temporary storage stations， and the service radius constraint and capacity constraint are considered in the location of temporary storage stations. A decomposition algorithm is used to solve the model， where an improved least point coverage heuristic algorithm is applied to the node location of temporary storage stations， and the k-means clustering algorithm is applied to the node location of terminal distribution stations. An example is used to verify the model and the algorithm. The result shows that the model and the algorithm can effectively solve the node location optimization problem of the urban express double-layer distribution network.

Key words：logistics planning; urban express delivery; double-layer distribution network; node location

收稿日期：2018-05-14

修回日期：2018-08-30

作者簡介：

杜剛誠（1977—），男，湖北秭歸人，高級工程師，碩士，研究方向為城市規劃、交通規劃，（E-mail）dgch2002@163.com

*通信聯系人。 （E-mail）ranlinna@126.com

0 引 言

近年來我國電子商務發展迅速，快遞業務量不斷增長，快遞作為物流產業的一個重要組成部分，逐漸滲透到社會經濟的各個領域。合理的配送網點布局可以提高配送資源的利用率，降低企業運營成本。以往快遞配送企業多采用單層配送模式。快遞單層配送網絡通常由兩級節點構成：一級節點即快遞分撥中心，一般設立在機場、鐵路貨站、公路貨站等大型交通樞紐，負責對快遞進行城市間的集散和轉運;二級節點即快遞末端配送站點，一般會設在各個城市分區，負責對快遞進行配送并兼顧快遞攬收業務。在這種單層配送模式下，快遞末端配送站點配送人員工作量過大，快遞配送效率低，因此，很多快遞配送企業已經開始采用雙層配送模式。快遞雙層配送網絡通常由三級節點構成：一級節點即快遞分撥中心;二級節點即快遞末端配送站點;三級節點即快遞便民寄存點。一般一個便民寄存點負責對一個或多個居民小區快遞的寄存和配送。為更好地服務客戶、擴大市場份額，研究快遞企業的網點布局及其優化具有現實意義。

近年來，針對快遞配送網絡的研究主要有：張哲輝[1]提出了快遞網絡的構成，即“取送—集散—網路”，并運用數學和管理學方法，詳細分析了快遞市場的發展因素;張蘭[2]建立了快遞網絡覆蓋模型和中轉場選址模型，并給出拆分和合并兩種模式下網點布局優化的策略;焦艷[3]將網絡成本最小作為最終目標，建立了基于城市電子商務的物流網絡選址多目標模型，采用遺傳算法和禁忌搜索算法分別對配送區域、選址分配、路徑優化問題進行了求解;叢迪悅[4]建立了快遞企業服務網點布局優化策略模型，建立了基于層次分析法和成本約束條件的目標規劃模型，最終完成了快遞網點整體布局優化;楊從平等[5]以配送時間和節點流量作為約束條件進行快遞網絡優化，將網絡配送總成本最小化作為優化目標，運用Floyd算法和Dijkstra算法進行了求解;盧文濤[6]在考慮時間閾值的基礎上構建了快遞網絡優化模型，基于成本懲罰和嚴格時間閾值構建了數學模型，同時用摩西網絡進行了演算;程賜勝等[7]在假定城市物流系統運行費用最低的條件下構建了城市物流節點選址模型，并用離散粒子群優化算法對該模型進行了求解。

上述研究主要針對快遞配送節點選址的模型和算法設計，較少涉及對快遞企業雙層配送網絡及其節點選址的研究。本文在分析城市快遞雙層配送網絡構成的基礎上，建立考慮便民寄存點服務半徑約束的快遞雙層配送網絡模型，并提出分解算法求解模型，分別就便民寄存點選址和末端配送站點選址提出改進的最少點覆蓋啟發式算法和k-均值聚類算法，借助算例進行了模型和算法的驗證。

1 考慮服務半徑約束的快遞配送網絡模型建立為提高快遞配送效率，便民寄存點選址需要考慮合適的服務范圍。從城市物流網絡規劃的角度出發，快遞末端配送站點與便民寄存點聯動配合形成網絡。城市快遞雙層配送網絡示意圖見圖1。

快遞雙層配送模式一方面能夠分割城市配送區域，便于快遞配送人員熟悉掌握地理位置，另一方面可有效減少單個配送點負責的客戶數量，提高快遞配送效率。在建立城市或區域的快遞配送網絡時，往往已知各快遞分撥中心的數量、位置和快遞業務量，只需進行末端配送站點和便民寄存點的選址。本文以居民小區中心點代表客戶點。

1.1 問題描述

某地區有若干居民小區，已知該地區快遞分撥中心數量、位置和各小區快遞業務量，現欲在各居民小區周邊建立便民寄存點，為各居民小區客戶提供上門配送快遞服務。若便民寄存點與居民小區中心點之間的距離超過限值則不予配送;選擇合適的位置建立末端配送站點。本文只考慮前期建設成本，不考慮后期運營成本，選擇改進的最少點覆蓋模型進行求解，建立模型的目標為用最少的末端配送站點和便民寄存點服務所有的客戶。

1.2 假設條件

為簡化配送節點選址問題，假設：（1）已知快遞分撥中心數量、位置;（2）各居民小區需求必須得到滿足，一個居民小區由一個便民寄存點服務;（3）便民寄存點多建在小區周邊，不宜過大，因此有容量限制;（4）末端配送站點沒有容量限制;（5）從各快遞分撥中心到各小區的快遞業務量已知;（6）便民寄存點有服務半徑約束，與小區中心點之間的距離超過限值即不予服務;（7）快遞以件計。

1.3 模型參數設定

N為居民小區（客戶）集合，i∈N;S為便民寄存點集合，j∈S;R為末端配送站點集合，k∈R;M為分撥中心集合，m∈M;l為便民寄存點服務半徑約束;qim為從分撥中心m配送到居民小區i的快遞量;qij為從便民寄存點j配送到居民小區i的快遞量;qjk為從末端配送站點k到便民寄存點j的快遞量;qkm為從分撥中心m到末端配送站點k的快遞量;qkk′為從末端配送站點k到末端配送站點k′的路徑上分配的快遞量;Qj為便民寄存點j的容量限制;A（j）為便民寄存點j所服務的居民小區的集合;B（i）為服務居民小區i的便民寄存點j的集合;C（k）為末端配送站點k所服務的便民寄存點j的集合;xj為0-1變量，xj=1表示備選點j被選中作為便民寄存點，否則xj=0;yk為0-1變量，yk=1表示備選點k被選中作為末端配送站點，否則yk=0;zmk為0-1變量，zmk=1表示分撥中心m與末端配送站點k之間有路徑連接，否則zmk=0;Qkk′為0-1變量，Qkk′=1表示末端配送站點k與k′之間有路徑連接，否則Qkk′=0。

1.4 模型建立

式（1）和（2）為模型建立的目標，式（1）表示用最少的便民寄存點服務所有的居民小區，式（2）表示用最少的末端配送站點覆蓋所有的便民寄存點。式（3）～（6）為模型的約束條件，式（3）表示居民小區的所有快遞量都被處理，式（4）表示一個居民小區只能由一個便民寄存點服務，式（5）為便民寄存點容量限制，式（6）為便民寄存點服務半徑約束。

2 求解算法設計

本文建立的模型需要求解以下問題：確定末端配送站點和便民寄存點的位置及其服務范圍。本文采用分解法進行求解，將該問題分解為兩個相互銜接的子問題，即先確定便民寄存點的位置及其服務范圍，然后求解末端配送站點的位置及其服務范圍，第二個子問題的解建立在第一個子問題解的基礎上。

2.1 便民寄存點選址求解算法

采用改進的最少點覆蓋啟發式算法求解，主要步驟如下：

步驟1 初始化。令所有qij=0，xj=0，并確定集合A（j），同時保證備選點i與j之間的距離小于服務半徑l。

步驟2 選擇下一個便民寄存點。在S中選擇xj=0且A（j）的模為最大的點j′為便民寄存點，即A（j′）=maxj∈M{A（j）}，xj′=1，并在S中剔除節點j′，即S=S{j′}。

步驟3 確定便民寄存點j′的覆蓋范圍。令zi=1， 居民小區i已被便民寄存點覆蓋0， 其他

令qi=m∈Mqim，將A（j′）中的元素按qi從大到小的順序分配給j′，直至j′的容量達到最大且不超過容量限制或A（j′）為空。為保證每個便民寄存點的最大利用率，若加入新元素后累計容量超過限制，則跳過該項嘗試下一元素，直到容量已滿或A（j′）為空。其中，對于i∈A（j′）且zi=0，將i指派給j′的方法為：令qij=qi，若qij（1-zi）≤Qj′，則Qj′=Qj′-qij（1-zi），zi=1，并在A（j′）和N中剔除居民小區i;若qij（1-zi）>Qj′，qij=0，則跳過該項嘗試下一居民小區。

步驟4 若N和S為空，則停止，否則更新集合A（j），轉步驟2。

2.2 末端配送站點選址求解算法

2.2.1 數量確定

假設：（1）所規劃區域的總面積為A′，快遞總需求量為G;（2）區域內的快遞需求量平均分布，各末端配送站點的規模相同，且位于其服務區域的中心;（3）相同規模的末端配送站點在區域內各處的建設費用相等，即末端配送站點的建設費用與位置無關。

設當區域的末端配送站點數為n時，區域內快遞配送總成本為Cz（n），Cz（n）又由快遞配送成本Cd和快遞配送站建設成本Cs兩項組成。由假設（1）和（2）有：每個末端配送站點服務范圍的面積a相同，a=A′/n;每個末端配送站點的快遞處理量g相同，g=A′/n。

末端配送站點配送的平均距離d與服務范圍面積a的平方根成正比，即d=θfa，式中：θ為平均配送距離參數，與配送區域的形狀有關，如當配送區域為圓形時θ可取0.376，當配送區域為正方形時θ可取0.383，當配送區域為長寬比為2∶1的長方形時θ可取0.42;f為非直線系數，一般可取1.2。

快遞配送的主要內容包括配貨、裝載、運輸、卸載、車輛返回等幾項工作，其中：配貨、裝載、卸載這3項工作的費用與運輸距離無關，只與快遞量成正比（設比例系數為b）;運輸、車輛返回這2項工作則與運輸距離成正比。因此，快遞的配送成本可表示為

式中：k′為快遞配送單位成本。末端配送站點的建設費用包括兩部分：一部分是征地、倉庫堆場建設、設備購買的費用，這部分費用與末端配送站點的規模成正比，亦即與快遞處理量成正比（設比例系數為r）;另一部分是固定費用C0，如附屬設施建設費用等。因此，末端配送站點的建設費用可表示為

總成本為

區域內快遞配送總成本Cz（n）與末端配送站點數量n之間的關系為

確定區域最佳末端配送站點數量問題就是要求整數n，使上式中Cz（n）取值最小。先設n為實數變量，Cz（n）為n的連續函數，令

比較在n分別為

分別表示不大于X的最大整數和不小于X的最小整數。當n=Gk′θfA′2C02/5時總成本最小。

2.2.2 選址算法

得到需建設的末端配送站點數量后，就可以開始進行選址。本文采用k-均值聚類算法進行求解。k-均值聚類算法基于各個類內的數據點與所在類質心的誤差平方和最小原則，將數據點分為具有相似特征的k個簇。也就是說，將含有n個樣本數據的集合X=

{s1，s2，…，sn}劃分為k類（C1，C2，…，Ck），其中每個數據點只能歸屬為一類。

k-均值聚類算法最小化目標函數為

式中：sj為第i類Sj中的樣本;mi為第i類的聚類中心，即第i類樣本數據的均值;sj-mi2為第i類內各樣本與聚類中心的歐氏距離。

3 算例分析

為分析模型算法有效性，選取某快遞配送企業在M市的業務情況作為算例進行驗證。某快遞企業將該市劃分為105個居民小區，在該市設有A、B、C、D等4個快遞分撥中心。為滿足客戶需求，該企業計劃在該市建立一個完善的配送網絡：首先，在居民小區周邊建立服務半徑為3 km的便民寄存點，客戶以居民小區中心點代替，本市所有居民小區周邊都可以建立便民寄存點，因此其備選位置集合即所有居民小區集合;其次，在合適位置建立合適數量的末端配送站點，并確定相應的配送方案。

圖2為該企業業務情況分布圖;表1列出了4個分撥中心和居民小區的編號和坐標，各節點之間距離用歐氏距離表示;表2列出了M市的4個分撥中心某天需要配送到各居民小區的快遞量。

3.1 便民寄存點選址

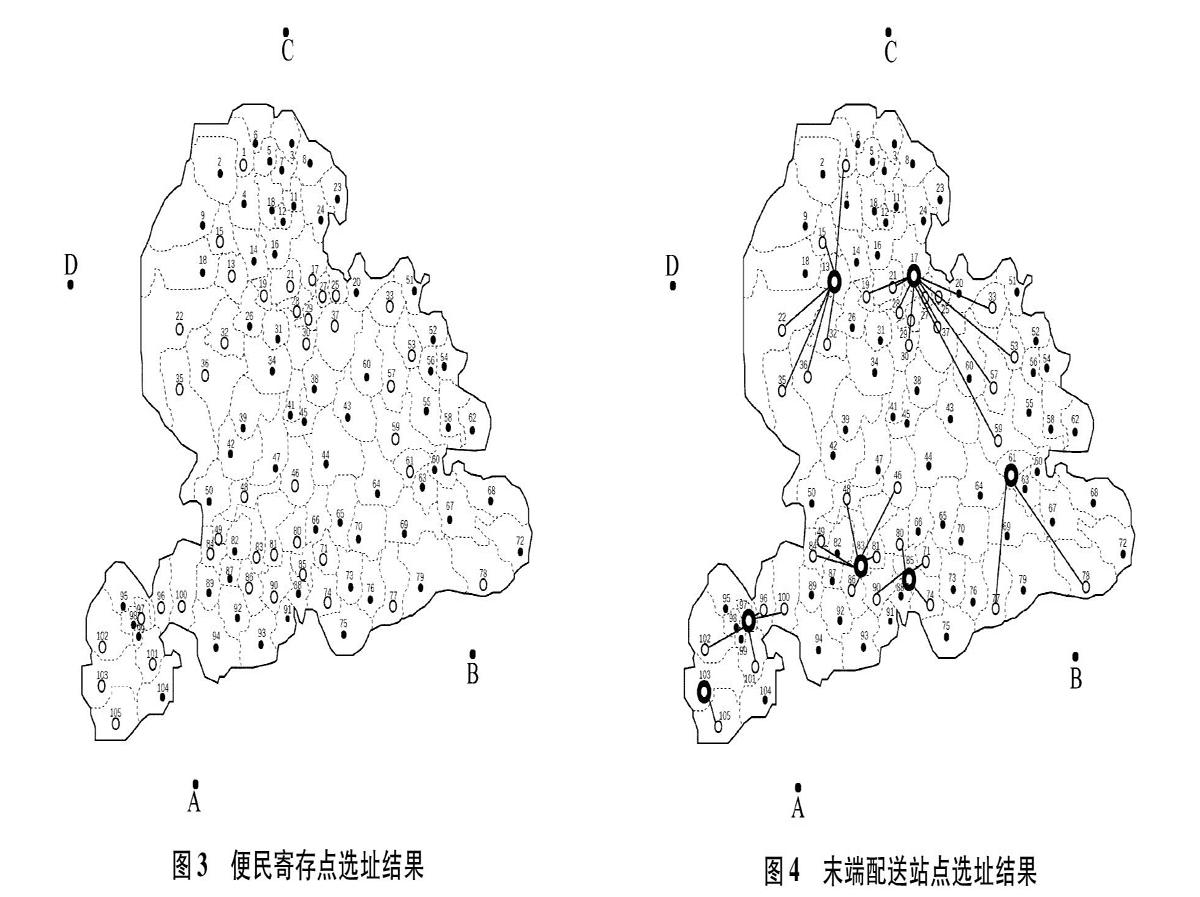
用MATLAB對模型算法進行編程求解，最終得到42個便民寄存點。表3為便民寄存點選址及分配方案，圖3為便民寄存點選址結果。

3.2 末端配送站點選址

末端配送站點數量計算。取G=26 142件，A′=294 km2，θ=0.42，f=1.2，C0=2億元，k′=0.02元/（件·km）（為市場調研均價），n=Gk′θfA′2C02/5，計算可得7個末端配送站點。

末端配送站點選址。在已選好的便民寄存點中選擇末端配送站點。假設可同時建設末端配送站點和便民寄存點，采用SPSS統計分析軟件，運用k-均值聚類分析方法，將42個便民寄存點按照空間聚類分為7個區域，選擇每個區域的聚類中心（或離聚類中心最近的點）作為末端配送站點位置。表4為末端配送站點選址及分配方案，圖4為末端配送站點選址結果。

3.3 算例結果分析

由表3、表4、圖3、圖4可得，區域內105個居民小區由4個快遞分撥中心，7個末端配送站點，42個便民寄存點負責M市快遞配送業務，便民寄存點與各居民小區中心點之間的距離不超過3 km。選址結果圖表明節點選址均勻，與居民小區距離合理。分配方案根據各自設施能力（便民寄存點服務半徑約束）及周邊居民小區需求緊迫性，已達成優化分配目的。選址及快遞量分配方案較合理，可有效降低快遞企業成本、提高配送效率、便于配送業務管理。算例結果表明本文所建立的模型符合實際，具

4 結束語

本文研究了考慮雙層配送模式的城市快遞配送網絡的構成及其優勢，從系統的角度對城市快遞雙層配送網絡進行了闡述。

本文建立了城市快遞雙層配送網絡的二級節點選址模型，提出分解算法求解模型。首先采用改進的最少點覆蓋啟發式算法進行便民寄存點選址;其次在便民寄存點選址的基礎上，采用k-均值聚類算法進行末端配送站點選址;最后通過算例進行模型和算法驗證，應用MATLAB編程實現了便民寄存點選址，應用SPSS軟件實現了末端配送站點選址。算例結果表明本文所提出的數學模型符合實際，所提出的分解算法能夠在較短時間內求解得到合理的解，具有一定的實用價值。

參考文獻：

[1]張哲輝. 快遞企業國內服務網點布局研究[D]. 大連：大連海事大學， 2005.

[2]張蘭. 快遞企業網點布局研究[D]. 長沙：中南大學， 2008.

[3]焦艷. 城市電子商務物流網絡優化設計與系統實現[D]. 上海：上海交通大學， 2013.

[4]叢迪悅. 快遞企業服務網點布局優化研究[D]. 大連：大連海事大學， 2014.

[5]楊從平， 鄭世玨， 黨永杰， 等. 基于配送時間及節點流量約束的快遞網絡優化[J]. 系統工程， 2015， 33（11）：53-59.

[6]盧文濤. 基于時間閾值的區域快遞網絡優化[J]. 溫州大學學報（自然科學版）， 2016， 37（2）：46-54.

[7]程賜勝， 蒲云虎， 高慧. 基于離散粒子群算法的城市物流節點選址模型[J]. 長沙理工大學學報（自然科學版）， 2008， 5（2）：20-24.

（編輯 賈裙平）