基于C0復雜度和GG模糊聚類的軸承性能退化狀態識別

王微，胡雄,王冰,孫德建

(上海海事大學 物流工程學院，上海 201306)

0 引言

港口起重機械是碼頭重要的物資裝卸設備，軸承是其起升機構中重要的旋轉支承部件，一旦發生突發性故障，輕則帶來經濟損失，重則導致人員傷亡。采集并分析軸承的運行監測信號，進而準確識別軸承性能退化狀態，能夠降低發生突發故障的概率，提升港口起重機械的運行可靠性。軸承性能退化狀態識別的關鍵步驟包括退化特征提取和識別模型構建[1]。

特征參數的優劣決定著性能退化狀態識別的準確性。常見的退化特征主要基于時域、頻域以及時頻域分析方法，其中時域、頻域指標因計算簡單且有應用價值而被廣泛采用，如信號的有效值、方差、峭度、平均頻率等[2-3]，但該類方法缺乏對信號的全面描述。時頻分析方法具有更好的多尺度分辨率特性，但本質上仍是基于線性分析，在面對非平穩和非線性的信號時的針對性不強。針對軸承振動信號非線性、非平穩性的特點，以信息熵為基礎的復雜度分析方法為該領域的研究提供了一條有效的途徑。應用較多的包括模糊熵[4]、樣本熵[5]、近似熵[6]等行為復雜度參數[7]，該類型方法通過度量短時間窗口中新模式的概率表征信號的復雜度。與行為復雜度相對應，結構復雜度則通過變換信號的頻率特性，結合信息熵分析信號的復雜度，典型方法即以Fourier變換為基礎的C0復雜度。C0復雜度主要應用在腦電以及語音信號的處理中，與行為復雜度相比具有計算量低，運算速度快，參數影響小等優勢[8-11]。然而，利用C0復雜度分析機械設備性能退化規律的研究較少，該方法具有在線特征分析的優勢和潛力。

由于機械設備的性能退化時間長，退化過程不可預知，退化狀態數目以及邊界難以確定，機械設備退化狀態的在線識別一直是該領域的難點問題。因此，嘗試通過無監督聚類方法分析特征數據的關聯性，挖掘數據之間的內在規律，識別不同的退化階段，完成退化狀態的無監督離線識別，從而為退化狀態在線識別奠定基礎。目前，應用較多的無監督聚類方法包括K均值聚類[12]，模糊C均值聚類(Fuzzy center means，FCM)[13]，GG模糊聚類(Gath-Geva fuzzy clustering,GG)[14]，GK聚類(Gustafaon-Kessel clustering, GK)[15]等。其中，GG模糊聚類算法采用了模糊最大似然估計距離范數，具有更優的聚類精度[16-18]。但目前GG聚類算法的研究熱點主要集中在軸承故障模式診斷中，對軸承性能退化狀態的聚類分析相對較少，而且對性能退化識別中時間連續性的約束考慮較少，算法的性能還有進一步提升的空間。

綜上，將C0復雜度應用于性能退化特征提取，采用logistics序列分析該參數的有效性，將時間參數映射到指數函數中，形成更符合退化過程的彎曲時間參數(Curved Time)，并與C0復雜度、有效值(RMS)構成三維退化特征向量，通過GG模糊聚類算法實現不同退化狀態的識別。

1 基于C0復雜度的退化特征分析

C0復雜度算法是一種非線性分析方法，無需對原始信號進行粗粒化處理，避免了信號動力學性質的改變，并且具有計算速度快的優勢[19]。C0復雜度的主要思想是以序列中非規則成分的比例定量描述信號的復雜度。對于一個長度M的一維時間序列{x(t),t=0,1,2,…,M-1},C0復雜度的計算步驟如下：

1)對x(t)進行離散Fourier變換可得

(1)

2)令WM=e-2πi/M，則

(2)

3)計算均方值GM

(3)

4)保留大于GM的頻譜，其余置零得

(4)

(5)

6)計算復雜度得

(6)

一般而言，C0復雜度能夠描述序列的復雜性，復雜度越大，序列波動模式越復雜，取值越大；復雜度越小，序列的波動模式越簡單，取值越小；因此，可以采用C0復雜度對機械設備的性能退化特征進行描述。

1.2 退化特征性能分析

Logistic混沌映射是研究動力系統、混沌、分形等復雜系統行為的一個時間離散動力系統[20]。本節以Logistic迭代作為仿真信號，分析C0復雜度在復雜度表征方面的規律和性能，信號表達式為

u(t+1)=λu(t)[1-u(t)],

(7)

式中：λ為非線性參數，λ∈[0,4]；u(t)為狀態變量，u(t)∈[0,1]；t為迭代次數。設置初始值為u=0.4，該方程的分叉圖如圖1所示。

圖1 Logistic混沌映射分叉圖

可以看出，當λ∈(3.00,3.57)時，系統處于周期狀態，并且周期個數在不斷變化；當λ∈(3.57,4.0)時，系統處于混沌狀態，同時一些狹小的區間混雜有周期性循環，使序列的復雜性下降。

分別計算每個λ取值下的C0復雜度，采用常用的熵分析方法進行對比，仿真計算機處理器為AMD A8-7600 Radeon R7，內存為8.00 GB，算法的參數及計算結果見表1，其中運行時間代表累計計算2 000次復雜度參數的總時間，Dim為嵌入維數，r為容差，τ為延遲因子。不同λ取值下的復雜度參數變化趨勢如圖2所示。

表1 算法參數以及計算結果

圖2 不同復雜度方法的變化趨勢

由圖2可知，C0復雜度和模糊熵能夠反映區間(3.00,3.57)中周期個數增多，復雜度逐漸增大的趨勢，近似熵和樣本熵算法則效果欠佳；同時，C0復雜度能夠清晰反映混沌態復雜度不斷增大的趨勢，對其中混雜的周期性循環導致復雜度下降的趨勢也能有所體現。從運算速度看，C0復雜度由于只涉及Fourier變換及其逆變換操作，運算速度遠優于其他3種方法。因此，C0復雜度參數與序列的復雜程度具有良好的關聯性，并且參數少，運算速度快，適合于在線退化特征的分析。

2 基于GG聚類的退化過程識別

2.1 GG模糊聚類評價指標

一般情況下，以模糊理論為基礎的聚類算法均是采用隸屬度最大原則進行類別聚類，判斷的數據依據為隸屬度矩陣U。應用較多的指標有分類系數(Classification Coefficient，CC)以及平均模糊熵(Average Fuzzy Entropy，AFE)[14]。CC指標越接近1，AFE指標越接近0，模糊聚類的效果越好。

此外，退化狀態聚類的主要特征是同一運行狀態的時間連續性。因此，提出一種序列離散度指標(Sequence Dispersion，SD)，以此衡量同一類別樣本時間標簽的連續性。對于某個聚類，假設I為該集合的標簽序列，n為該聚類的樣本個數，m-1為該標簽序列最大值與最小值之差，定義該聚類的序列離散度為

b=(m-n)/m，

(8)

顯然，如果I為連續序列，則b=0；I越不連續，序列中存在“空位”越多，序列離散度越大。

假設整個樣本集合被劃分為c類，則此次聚類的時間序列離散度為

(9)

該指標越接近于0，代表時間聚集度越高，退化狀態聚類效果越好；取值越大，時間聚集度越低，聚類效果越差。

2.2 退化過程識別流程

基于C0復雜度與GG模糊聚類的退化狀態識別方法如圖3所示。以機械設備全壽命數據為基礎進行退化狀態離線劃分，首先提取三維特征向量對退化狀態進行GG模糊聚類，然后通過3個指標對聚類效果進行評價。

選取有效值CRMS，C0復雜度以及時間彎曲參數CCT構成了三維特征向量[CRMS,C0,CCT]。其中，CRMS能夠表征信號的能量累積規律；C0復雜度能夠反映信號復雜度變化；CCT用于在狀態聚類時考慮同一種退化狀態在時間尺度上的集聚度。計算方法是將全壽命數據中的時間參數T歸一化并映射到函數CCT=eT-1中，從而獲得初期平緩，后期劇烈的“彎曲時間維度”，從而更準確地反映機械設備性能退化的時間分布特性,如圖4所示。

3 退化狀態識別實例分析

3.1 軸承全壽命數據試驗

軸承全壽命數據集來自辛辛那提大學IMS中心[21],加速試驗臺示意圖如圖5所示。試驗中采用的軸承類型為Rexnord ZA-2115雙列圓柱滾子軸承，滾子數量為16，滾子組節圓直徑為75.501 mm，滾子直徑為8.407 mm，接觸角為15.17°。

圖5 加速試驗臺結構示意圖

選取其中一組數據集進行分析，該組試驗的加載力為5 000 N，轉速為1 500 r/min，采樣頻率為20 kHz，每組采樣時間為1 s，組間采樣間隔為10 min，共采集984組數據。試驗臺停機后檢查發現軸承1出現故障，失效形式為外圈滾道面磨損；其余3套軸承均完好。忽略數據集的采樣間隔，軸承性能退化的時域波形如圖6所示。信號幅值在第700組采樣點開始出現增大的趨勢，需要進一步進行退化特征分析。

圖6 軸承全壽命數據的時域波形

3.2 退化特征提取

分別對每組采樣數據進行退化特征分析，計算C0，CRMS及CCT。為降低不同量綱對聚類效果的影響，對3個特征指標進行量綱一化。C0的計算中，參數r設置為10。軸承全壽命數據集的退化特征趨勢如圖7所示。由圖可知：1)從整體趨勢上看，C0隨著性能退化程度加深而逐漸降低，CRMS的趨勢則與之相反；說明隨著性能退化程度的增加，信號中的隨機成分逐漸減少，信號的復雜度隨之降低；而從能量累積角度分析，信號的能量隨著退化程度的增加而不斷增大，CRMS也隨之增大。2)從細節上看，C0和CRMS均呈現出一定的階段性，反映了軸承性能退化的不同狀態；而通過時間的“彎曲化”，CCT與性能退化的整體趨勢關聯性更強。

圖7 軸承全壽命數據的性能退化特征趨勢

3.3 退化狀態識別

對軸承退化狀態進行GG模糊聚類，參考同類文獻[22-23]將退化狀態劃分為4類：正常、輕微退化、嚴重退化、失效。設置參數為c=4，m=2，容差為ε=0.000 01，對不同的退化狀態進行無監督GG聚類，聚類效果的等高線圖如圖8所示。由圖可知，GG聚類算法的等高線為任意形狀，說明該算法對數據源的分布要求較低，具有更好的適應性。

圖8 GG聚類等高線示意圖

GG聚類的軸承退化狀態識別結果如圖9所示，整個退化過程同樣聚集為了上述4種狀態，且各個狀態在時間尺度的連續性均較好。

圖9 GG聚類效果圖

由圖9可知：1)CRMS反映了性能退化過程中的能量積累情況，因此取值隨著退化程度的加深而逐漸增大。2)CCT反映了性能退化的時間標度，呈現嚴格的單調性。3)在約第520組采樣點之前，軸承一直保持較長時間的正常狀態，C0維持在0.7附近；當軸承性能輕微退化時，C0非常敏感且快速下降，并出現明顯的波動現象；進入到約第820組采樣點后，軸承性能嚴重退化，C0基本維持在0.4左右，數值反彈不大；當進入到失效狀態時，C0取值低于0.4且出現一些數值異常的離散點，此時認為軸承已經完全失效。

3.4 對比分析

3.4.1 時間特征參數對聚類效果的影響

首先分析時間特征參數對于聚類效果的影響。保持GG模糊聚類算法和參數設置不變，分別采用二維特征[C0，CRMS]和三維特征[C0，CRMS，T]進行對比分析，結果如圖10和表2所示，其中T為未進行映射的時間參數。對比分析可知，3種方法在分類系數上取值相近，但文中方法的平均模糊熵和序列離散度最低，說明聚類的時間集聚性和聚類效果最優。

圖10 選取不同特征參數的聚類效果圖

表2 不同特征參數的定量評價結果

3.4.2 聚類算法對聚類效果的影響

保持三維特征向量[C0，CRMS，CCT]不變，分別采用GK聚類、FCM聚類與GG聚類進行對比分析，結果如圖11和表3所示。對比分析可知，由于引入了CCT，3種算法的序列離散度均較低，說明分類的時間集聚度得到了提高。但GK和FCM聚類算法的平均模糊熵仍較高，說明模糊矩陣U中的隸屬度取值相近，算法在進行模糊決策時容易造成狀態誤判，例如圖11a中GK聚類算法將第500組采樣點后出現的輕微退化狀態誤判為正常狀態。GG聚類算法采用了模糊最大似然估計距離范數，模糊矩陣的隸屬度區分較大，分類系數和平均模糊熵的取值更優，易于做出正確的決策。

圖11 不同特征參數的一維聚類效果圖

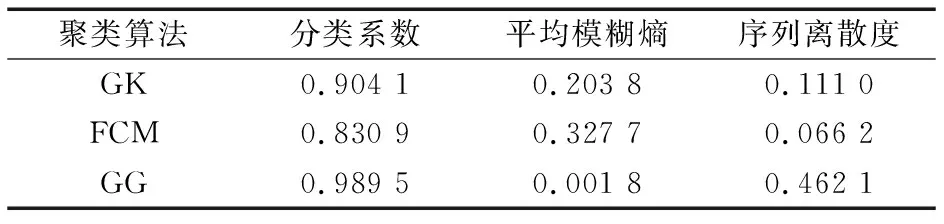
表3 不同聚類算法的定量評價結果

綜上所述，C0復雜度具有良好的性能退化指示能力，結合彎曲時間參數和有效值能夠構成科學的退化特征向量；通過GG聚類算法良好的聚類性能，能夠科學地識別軸承性能退化狀態。

4 結論

提出了基于C0復雜度與GG聚類的退化狀態劃分方法，通過實例數據的分析驗證得到以下結論：

1)C0復雜度能夠反映信號中不規則成分的比例，有效描述性能退化過程中的規律性，對復雜度變化十分敏感。

2)彎曲時間參數能夠反映采樣數據的時間特征，并且通過對指數函數的映射操作使其更符合機械設備的性能退化規律。

3)GG聚類方法能夠對任意形狀的數據進行聚類，將時間約束加入到特征向量中，能夠在保持聚類精度的同時提高類別內部的時間聚集度。所提出的序列離散度指標參數較好地反映出了聚類的時間聚集效果。