汽車主減速器圓錐滾子軸承的最佳軸向預緊量
廖鑫,周獻文,高俊聰,蔡萬野,翟敬宇
(1.大連理工大學 機械工程學院,遼寧 大連 116024;2.遼寧重大裝備制造協同創新中心,遼寧大連 116024;3.瓦房店軸承集團 國家大型軸承工程技術中心,遼寧 瓦房店 116300)
圓錐滾子軸承廣泛應用于汽車、機床、機車等重型機械中,其使用性能及壽命直接影響設備的正常運轉[1]。圓錐滾子軸承可同時承受較大的徑向、軸向聯合載荷,安裝時需施加一定的軸向預緊量以消除軸向游隙,軸向預緊量會直接影響軸承的內部接觸狀態和使用壽命[2-4],故有必要分析軸向預緊量對軸承使用性能及壽命的影響。
國內外學者對軸承預緊做了大量研究,文獻[5]分析了角接觸球軸承預緊力與位移、軸向力、疲勞壽命的關系;文獻[6]分析了軸向預緊力對角接觸球軸承模態特性的影響;文獻[7]分析了軸向、徑向預緊力對軸承動態特性的影響;文獻[8]分析了角接觸球軸承接觸載荷和鋼球的運動規律,得到了防止鋼球陀螺滑動所需的最小預緊力;文獻[9-10]分析了過盈配合和軸向預緊力對角接觸球軸承性能的影響;文獻[11]建立圓錐滾子軸承內部載荷的計算模型,得到了預緊力-壽命特性曲線。上述研究從理論上分析了預緊力對軸承力學性能和疲勞壽命的影響,但均未分析預緊量與軸承使用壽命的關系。鑒于此,以某型汽車主減速器用圓錐滾子軸承為研究對象,在分析輸出軸傳動系統受力的基礎上,考慮汽車運行中主減速器齒輪的嚙合效應,基于Romax建立傳動系統力學模型,分析了圓錐滾子軸承軸向預緊量對軸承內部接觸狀態和疲勞壽命的影響。
1 載荷計算
以某型汽車單級錐齒輪減速器為例分析,汽車整車參數[12]見表1,不同擋位的傳動比見表2。整體結構圖如圖1所示,所采用的單級減速器的輸出軸兩端由2個FAG30313A圓錐滾子軸承支承(1#軸承在輸出軸左端,2#在輸出軸右端),圓錐滾子軸承結構如圖2所示,其主要結構參數見表3,輸出軸系統中從動錐齒輪的主要參數見表4。

表1 整車參數Tab.1 Vehicle parameters

表2 不同擋位的傳動比Tab.2 Transmission ratios for different gears

1—輸出軸;2—從動錐齒輪;3—輸入軸;4—主動錐齒輪
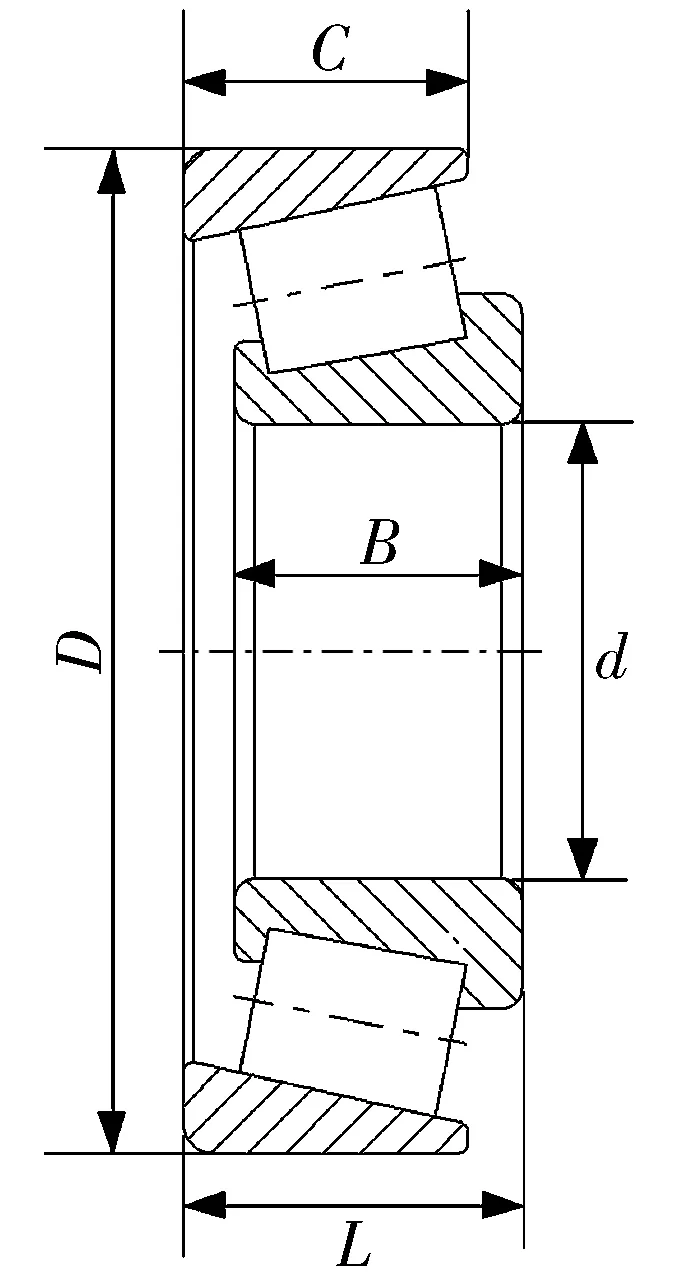
圖2 圓錐滾子軸承結構Fig.2 Structure of tapered roller bearing

表3 軸承主要結構參數Tab.3 Main structural parameters of bearing

表4 從動錐齒輪主要參數Tab.4 Main parameters of driven bevel gear
發動機輸出的動力通過齒輪嚙合由減速器的輸入軸傳遞到輸出軸,軸承可簡化為固定鉸支座,輸出軸系統的受力如圖3所示。圖中:FN1,FN2分別為1#,2#軸承的支反力;F1,F2分別為1#,2#軸承的軸向力;Fa為從動錐齒輪的軸向力;Fr為從動錐齒輪的徑向力;Ft為從動錐齒輪的圓周力。
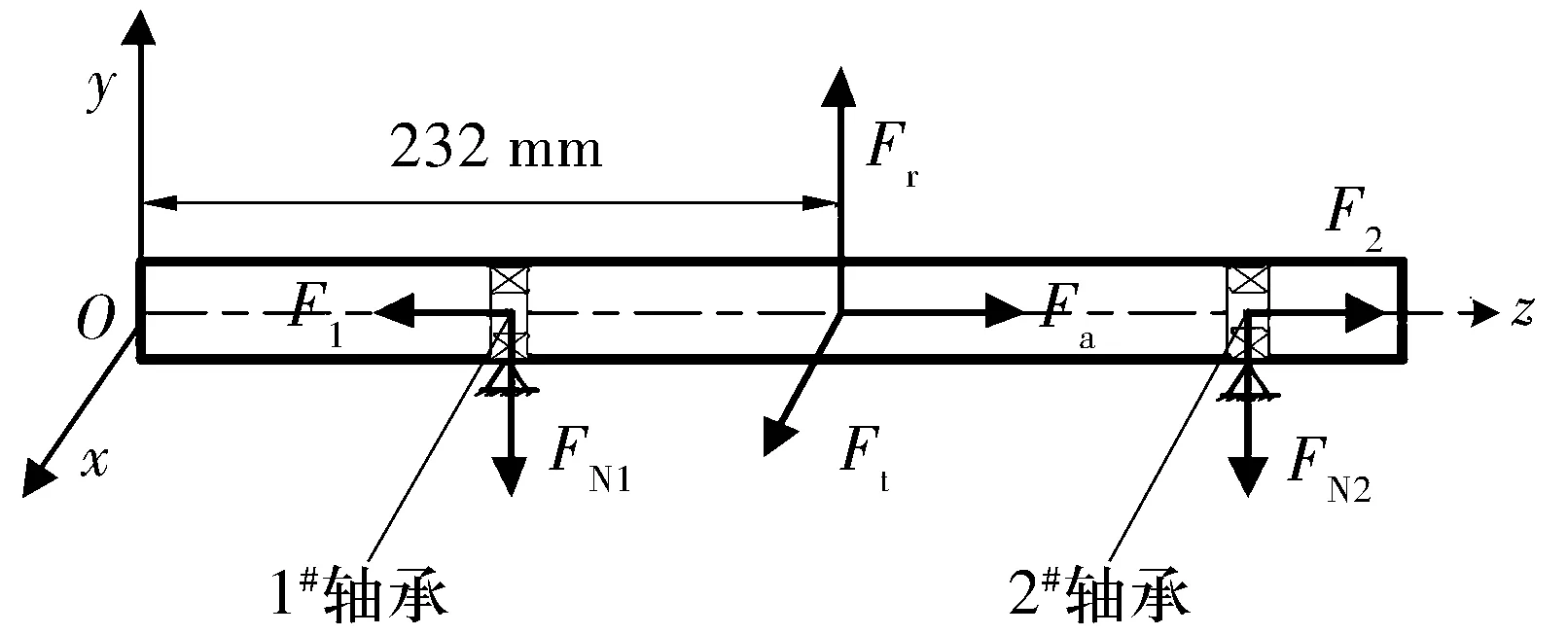
圖3 輸出軸系統受力示意圖Fig.3 Load diagram of output shaft system
為簡化模型,基于Romax建立傳動系統模型時忽略齒輪,將齒輪傳動產生的力和力矩等效施加于輸出軸相應位置。軸系平衡方程為
Fr=FN1+FN2,
(1)
F1=Fa+F2。
(2)
為得到不同工況下齒輪傳動產生的載荷,對主動錐齒輪進行受力分析,如圖4所示。將名義法向載荷Fn在主動小齒輪平均分度圓處分解為圓周力Ft1(Ft1=Ft)、徑向力Fr1(Fr1=Fr)及軸向力Fa1(Fa1=Fa),根據力平衡條件和各力之間的幾何關系可得
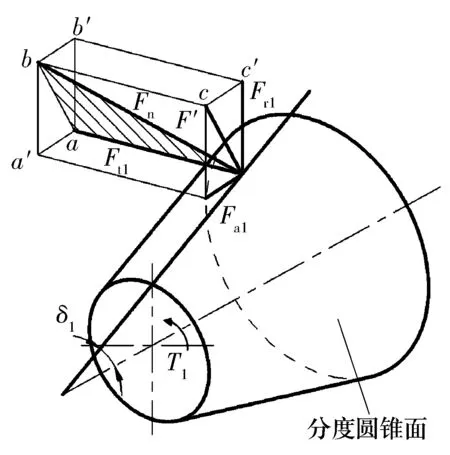
圖4 齒輪受力示意圖Fig.4 Load diagram of gear
(3)
Fr1=Ft1tanαcosδ1,
(4)
Fa1=Ft1tanαsinδ1,
(5)
Fn=Ft1/cosα,
(6)
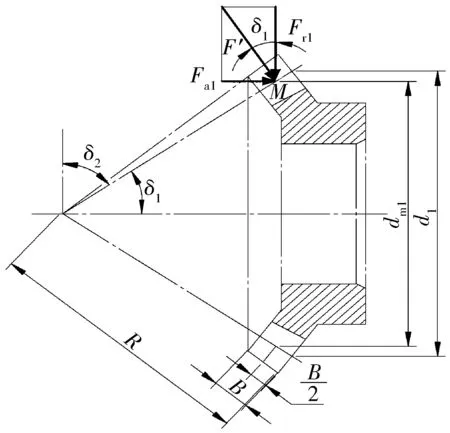
式中:dm1為參考點M的分度圓直徑;T1為主動齒輪傳遞的轉矩;δ1為齒輪分錐角;α為齒輪壓力角。
汽車實際運行中工況復雜,僅分析其中3種典型工況[13]:1)工況1為汽車在平穩路面上以3擋低速行駛;2)工況2為汽車啟動,發動機輸出最大轉矩且傳動系選擇最低擋;3) 工況3為汽車滿載,驅動車輪打滑。3種工況下從動錐齒輪扭矩分別為
T1=TEi3i0K0ηT,
(7)
T2=Temaxi1i0K0ηT,
(8)
(9)
式中:TE為額定功率時的發動機轉矩;i3為變速箱3擋時傳動比;i0為主減速器傳動比;K0為超載系數,一般取為1;ηT為發動機到從動錐齒輪間傳動部分的效率,取0.9;Temax為發動機最大轉矩;i1為變速箱1擋時傳動比;G為汽車滿載時驅動橋對水平地面的最大載荷;φ為輪胎對路面的附著系數,取0.85;r為車輪滾動半徑;ηLB,iLB分別為主減速器從動輪到驅動輪之間的傳動效率和減速比,分別取0.95和1。
通過(1)~(9)式可得3種典型工況下從動錐齒輪的載荷見表5。

表5 3種典型工況從動錐齒輪的載荷Tab.5 Loads of driven bevel gear under three typical operating conditions
2 建立模型
Romax Designer是一種應用于機械傳動系統虛擬產品開發與模擬的平臺,可對減速器和變速箱等傳動系統建模、設計及分析。與ANSYS等有限元軟件相比,Romax具有快速建模、精確仿真等特點,在汽車軸承等領域廣泛應用,在此采用Romax對汽車主減速器圓錐滾子軸承的預緊量進行計算。
由圖4可知,齒輪傳動時在距離輸出軸左端232 mm處會產生x,y,z軸3個方向的力和1個力矩,考慮到研究對象是輸出軸單軸系統,建模時忽略從動錐齒輪,把齒輪傳動產生的力和力矩等效加載在輸出軸相應位置。在Romax軟件中,根據圖1結構分別添加FAG30313A軸承在軸段相應位置,軸承外圈固定。軸的工作轉速為350 r/min,將表5工況的載荷施加在輸出軸上,得到輸出軸-軸承傳動系統Romax簡化模型,如圖5所示。
圖5 Romax模型Fig.5 Romax model
3 預緊量對軸承性能的影響分析
以1#軸承為例,基于Romax Designer對軸承載荷分布、接觸應力和使用壽命等進行分析。
3.1 預緊量對載荷分布的影響
將表5中不同工況對應的載荷施加在Romax模型中,得到預緊量與受載滾子數量的關系如圖6所示。從圖中可以看出,隨預緊量增大,受載滾子數量逐漸增多直到全部滾子受載,這是因為隨預緊量的增加,軸承扇形受載區域逐漸增大。
由于輸出軸工作轉速較低,滾子離心效應影響較小,滾子與內、外圈的接觸載荷基本相同。主要以滾子與內圈的接觸載荷為例分析,最大接觸載荷隨預緊量的變化如圖7所示,從圖中可以看出:隨預緊量增大,滾子與內圈的最大接觸載荷呈先減小后增大的趨勢;隨徑向載荷增加,最佳預緊量也逐漸增大。
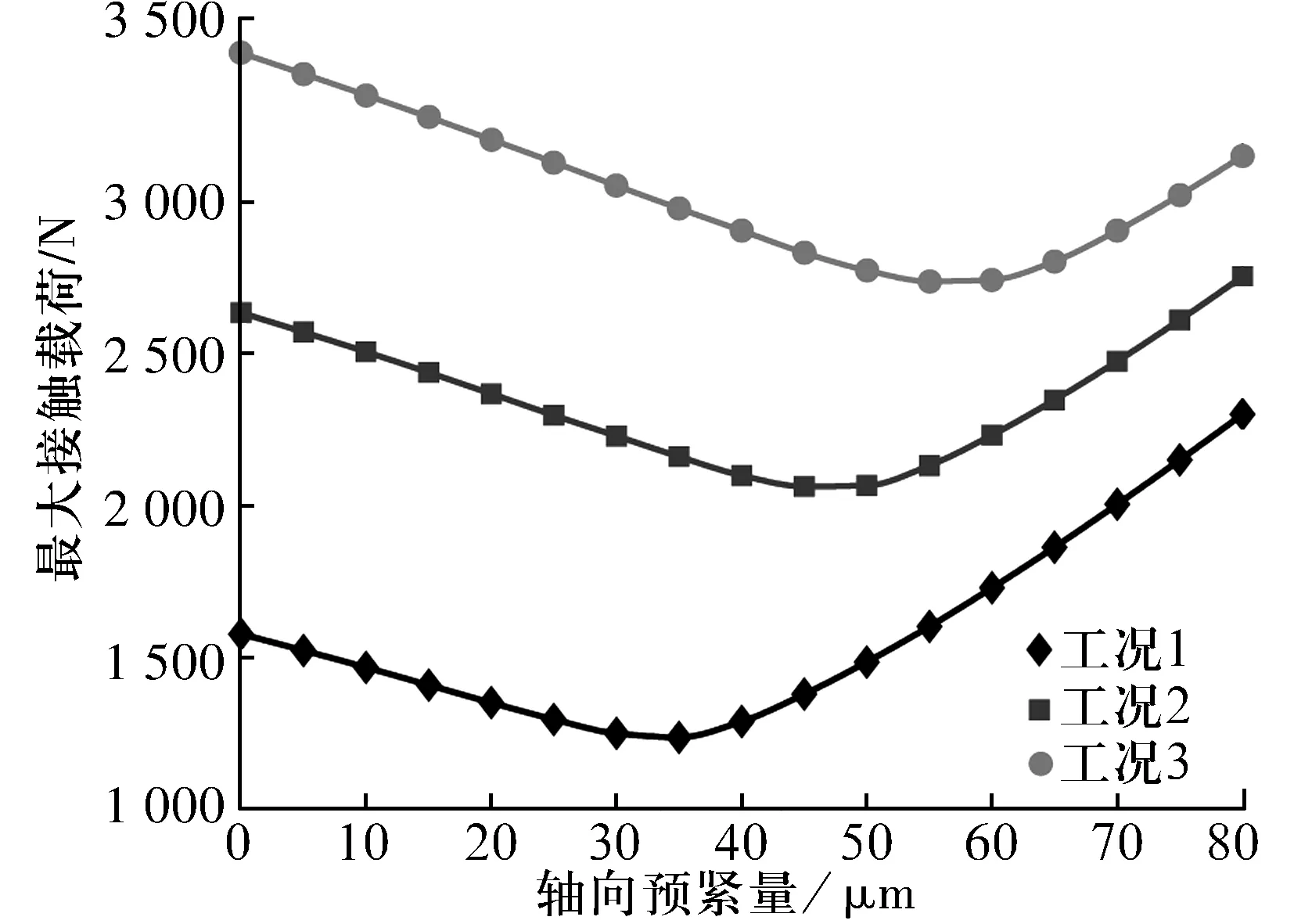
圖7 最大接觸載荷隨預緊量的變化曲線(內圈)Fig.7 Variation curves of maximum contact load with preload(inner ring)
3.2 預緊量對軸承接觸應力的影響
最大接觸應力隨預緊量的變化曲線如圖8所示。從圖中可以看出:隨預緊量增大,最大接觸應力先減小后增大,這是由于隨著預緊量增大,軸承受載區的滾子數不斷增大,最大接觸應力減小;當軸向預緊力增加到一定程度時,受載滾子數不變,隨預緊量增大,最大接觸應力增大。
3.3 預緊量對軸承壽命的影響
滾動軸承的壽命計算主要參考ISO 281:2007 《Rolling bearings—dynamic load ratings and rating life》,在Romax中選擇ISO281 Rev2(2007)壽命計算標準,考慮了潤滑油液等的影響,其中潤滑劑選擇ISO VG100礦物油,工作溫度為70 ℃。分析得到軸承壽命(L10h)隨預緊量的變化如圖9所示,從圖中可以看出:隨預緊量增大,軸承壽命呈先增大后減小的趨勢;當預緊量過大時,軸承壽命急劇下降。
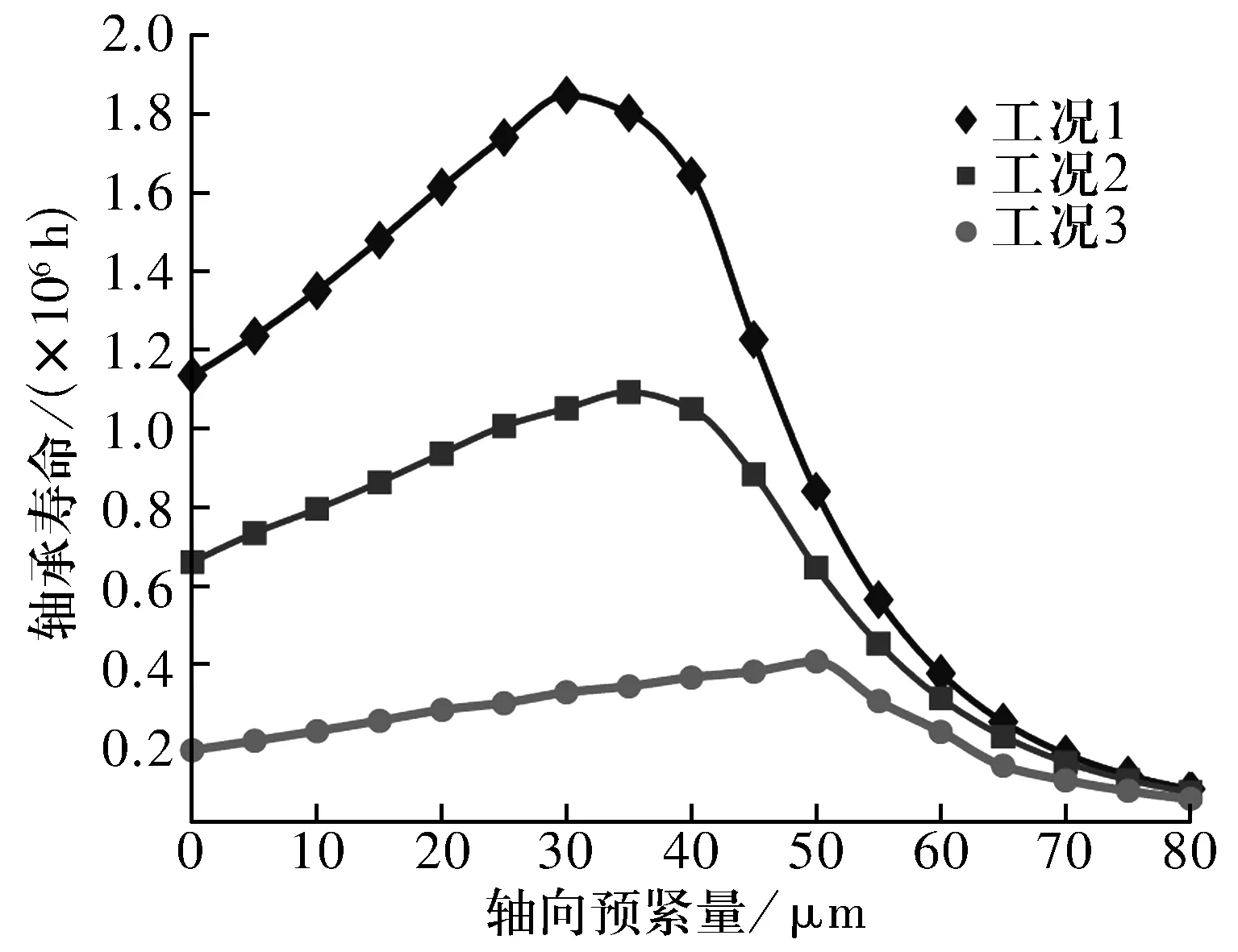
圖9 壽命隨預緊量的變化曲線Fig.9 Variation curves of life with preload
在不同徑向載荷下分析軸承預緊量對其壽命的影響規律,得到不同徑向載荷作用下軸承壽命最大時的最佳軸向預緊量,如圖10所示。從圖中可以看出:隨徑向載荷的增大,最佳軸向預緊量近似呈線性增大。
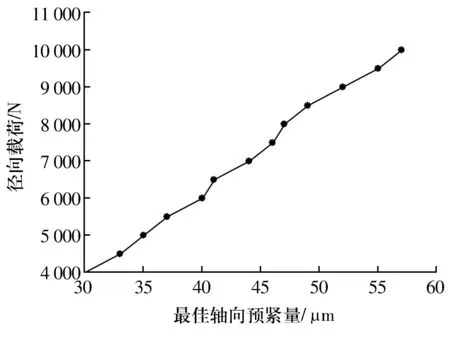
圖10 不同徑向載荷作用下的最佳軸向預緊量Fig.10 Optimal axial preload under different radial loads
4 結論
基于Romax分析了不同載荷工況下軸向預緊量對圓錐滾子軸承內部接觸狀態和疲勞壽命的影響,得出以下結論:
1)隨軸向預緊量增大,受載滾子逐漸增多直至全部受載,最大接觸載荷及最大接觸應力呈先減小后增大的趨勢。
2)隨軸向預緊量增大,軸承壽命先增大后減小,存在最佳軸向預緊量使軸承壽命最佳。
3)最佳預緊量隨徑向載荷的增大而逐漸增大,且近似呈線性關系。

