金屬切削加工本構模型研究進展*

呂明航， 李安海,2， 呂豪劍， 葛德俊

(1. 山東大學 機械工程學院， 高效潔凈機械制造教育部重點實驗室， 濟南 250061)(2. 山東大學， 機械工程國家級實驗教學示范中心， 濟南 250061)

在金屬切削加工過程中，復雜的熱力現象制約著加工技術的發展。隨著計算機技術的發展，采用有限元方法來模擬加工過程，研究加工過程中復雜的熱力耦合現象，成為一種重要的研究方向。而本構模型表征了材料應變、溫度、應變速度等變形參數，決定了材料的力學行為[1]。因此，建立的有限元模型能否與真實加工精確吻合，本構模型是關鍵[2]。

為了準確地對加工過程進行仿真，國內外學者采用多種方法對本構模型進行了修正，主要分為唯象本構和物理本構2大類[3]。本文從幾種常用的本構及其修正模型、模型中原始參數確認方法等方面進行總結及分析，為加工本構模型的建立和應用提供參考。

1 常用本構模型及其修正

1.1 Johnson-Cook模型及其修正

Johnson-Cook模型(JC模型)是由Johnson和Cook[4]在1983年提出的。該模型綜合考慮金屬材料加工過程中應變、應變率、溫度等因素對流動應力的影響，建立了應變強化、應變率強化和溫度軟化的函數，可用于大變形、大應變率條件下的材料變形行為，模型的形式為：

(1)

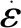
由于JC本構模型結構形式簡單，且所需的材料參數較少，便于通過實驗獲取，在切削加工仿真中應用廣泛。但是由于加工中會發生復雜變化，JC本構在某些情況下不能很好地反映加工的真實情況，因此各國學者對其做了大量的修正工作。

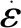
(2)

CHEN等[6]在對Ti-6Al-4V鈦合金分離式霍普金斯壓桿實驗(SHPB)實驗中發現應變硬化與溫度相關，其隨溫度的變化會對流動應力產生影響。因此，他定義了一個溫度函數Δ(T)來表征這種特性。柯志宏[2]在鈦合金切削仿真中，在JC本構的基礎上加入CHEN所定義的溫度函數，形成新的模型：

(3)

KHAN等[7-8]在對鈦合金的研究中發現塑性應變和應變速率之間存在著很強的相關性，二者相互作用對流動應力造成一定的影響。為了正確反映二者的相互影響，在JC模型基礎上將應變強化項中的塑性應變與應變速率進行耦合，建立新的KHL模型：

(4)

CHENG等[9-10]在研究中發現加工過程中不同應力狀態的變化也會對流動應力產生影響，因此在JC本構方程的基礎上進行修正，加入應變狀態項[1-cη(η-η0)]，形成新的本構方程：

(5)

ANDRADE等[11]在純銅壓縮實驗中發現了在一定溫度范圍內流動應力隨溫度升高而降低的現象，認為這是由于材料內部再結晶軟化的影響，從而提出在JC本構模型的基礎上引入與再結晶溫度有關的函數H(T)來修正這一現象。SEO等[12]將此本構模型應用于鈦合金Ti-6Al-4V的加工仿真過程中，發現這種本構同樣適用：

(6)

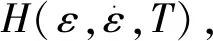
(7)

劉麗娟等[15-16]在對鈦合金高速銑削切屑形態的微觀研究中，發現由于加工過程高溫和大變形的作用，使絕熱剪切帶發生動態再結晶現象，這使得材料軟化程度增大，對材料的流動應力產生影響，促進了鋸齒形切屑的形成和發展。在此基礎上，建立了反映動態再結晶行為的本構方程：

(8)

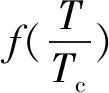
王琪等[17]在對鈦合金高速切削研究中，同樣發現溫度達到臨界溫度時，材料會發生動態再結晶行為，使材料流動應力下降的現象。但他們對JC本構進行了不同的修正，采取引入一個連續溫度函數式Y(T)的方法來反映鈦合金在各個溫度下的真實流動應力變化情況：

(9)

程國強等[18]在對HY-100鋼的研究中，發現材料內部缺陷和夾雜在加工過程中會擴大聚集形成孔洞，到一定程度后產生破壞，會對材料的流動應力產生影響。通過在JC本構模型的應變項中增加反應材料損傷的軟化項來修正：

(10)

滑勇之等[19]研究鋁合金時，發現鋁合金在到達一定溫度時，材料會發生急劇軟化，而JC本構中的熱軟化項無法滿足材料的特性曲線，為了更好地描述這一特性，對熱軟化項Kt進行了修正：

(11)

CALAMAZ等[20]在對鈦合金加工研究中，發現流動軟化和應變軟化等因素對流動應力的影響很大，因此在原本構模型的基礎上引入分別反映應變軟化和流動軟化的修正項，形成新的Hyperbolic Tangent本構(TANH本構)：

(12)

這種本構模型被李川平等[21-23]采用。并且YAMEOGO等[23]認為新加入的軟化項只有在重結晶發生時才會起作用，因此在仿真中同時使用JC本構和TANH本構，通過檢測應變值是否達到臨界值來確定哪種本構生效：

(13)

1.2 Zerilli-Armstrong本構模型及其優化

Zerilli-Armstrong模型(Z-A模型)是由Zerilli和Armstrong提出的[24]。Z-A模型是基于位錯動力學形成的，能夠很好地反應體心立方金屬和面心立方金屬的熱變形行為，表達形式簡單，獲得了廣泛的應用。

面心立方金屬材料本構方程為：

(14)

體心立方金屬材料本構方程為：

(15)

Zerilli和Armstrong在之后的研究中，對模型不斷優化，建立了適用于密排六方金屬的本構方程，并通過鈦合金Ti-6Al-4V實驗驗證了其可行性。

(16)

但是Z-A模型也存在局限性，模型中的應變硬化率與溫度和應變率之間的影響是相互獨立的，但是大多數金屬三者之間是相互耦合的，因此Z-A模型不適合于描述三者之間有強相關性的材料。

LIU等[25-26]在進行Ti-6Al-4V加工仿真時，發現傳統的Z-A模型未能夠反映剪切帶形成過程中材料孔洞、微裂紋等對流動應力的影響。因此，其在原模型的基礎上引入多重失效函數來表征這種現象：

(17)

1.3 GAO-ZHANG本構模型

除了常用的JC本構和Z-A本構模型外，國內外學者基于基礎理論提出了新的本構模型。GAO等[27-28]在仿真密排六方金屬加工時，以熱激活位錯理論為基礎，建立了新的本構模型GAO-ZHANG模型(G-Z模型)。在此模型中，等效應力是由非熱應力項和熱應力項組成的：

(18)

1.4 多物理場模型

SHEN等[29-30]在對銅和鋁合金切削仿真研究中，提出了一種基于位錯密度的晶粒細化子模型，其原理如圖1所示，通過模擬晶胞的拉長、細化等過程來體現加工過程的微觀作用，修正流動應力。

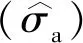
(19)

同時，為了體現微觀變化對流動應力的影響，ATMANI將臨界應力模型和位錯密度模型相結合，建立了一種多物理場模型，其耦合方式如圖2所示。

2 本構模型參數的優化方法

本構方程的形式對仿真結果有影響，模型中的初始參數對于仿真結果也有很大的影響，因此眾多學者對本構模型中原始參數的確定進行了大量的研究[33]。為了提高本構模型的修正精度，彭臣西等[34-35]采用單因素仿真實驗方法探究JC本構模型5個系數(A、B、n、C、m)對切削力、切屑形態以及參與應力分布狀態的影響。FENG等[36-37]通過熱壓縮試驗測得鋁、鈦合金在特定溫度范圍的應力、應變值，確定了本構方程的原始參數。SEO等[12]采用分離式霍普金斯壓桿實驗(SHPB)研究了高溫下鈦合金的應變行為，并對本構方程中的原始參數進行了擬合。汪冰峰等[38]在根據SHPB實驗數據擬合方程時，采用引入應力應變取向發展趨勢項的方法，分兩步擬合曲線，簡化對溫升等因素的估算。魯世紅等[3]利用SHPB實驗所測到的數據，通過MATLAB應用自適應遺傳算法來優化本構模型中的原始參數。

雖然SHPB實驗被廣泛應用于本構方程原始參數的確定過程中，但這種方法存在著一定的局限性：(1)SHPB實驗所能達到的應變和應變率與真實切削加工還存在差距；(2)SHPB實驗需要特殊的測試儀器且測試費用昂貴。因此，研究人員探索通過其他方式來獲取原始參數。SHATLA等[39]開發了專用的計算機軟件《OXCUT》來獲取數據修正模型的原始參數。李川平[21]通過將正交切削實驗數據與有限元仿真數據比較、迭代的方法，修正了鈦合金在大應變、高應變率條件下的本構模型材料常數。葉玉剛等[40]在確定本構模型初始值時，在魯世紅等[3]所測參數的基礎上，對多次有限元實驗采用下山單純型法迭代來確認原始參數。

楊勇等[41]提出有限元模擬和單因素流動應力公式計算聯合建模的策略。先由單因素公式計算出與應變率對應的流動應力，再基于新的流動應力進行有限元迭代分析，通過反復迭代最終得到準確的本構方程。

上述本構方程在確定原始參數的過程中，每個參數是分別擬合的，而GAO等[27]認為單獨擬合確定的參數不是整體上的最優解，因此提出采用全局算法和局部算法相結合的多目標非線性優化法來確定本構模型的最優原始參數，此方法確定的本構方程在仿真過程中得到更加精確的結果，其優化流程如圖3所示。

3 結語

本構方程在金屬加工仿真過程中有重要作用，目前對于本構方程的研究有了長足的發展和進步，但在以后的研究中還需要關注以下方面：

(1)對本構模型的建立只考慮了再結晶等變形機制的影響，對于加工過程中微觀復雜的變化對流動應力影響的研究還不夠深入，同時對宏微觀作用的綜合研究還不夠完善。依據宏微觀作用機制，建立多物理場耦合的本構模型是未來的研究方向。

(2)由于本構模型中原始參數的確定還不夠準確，目前經過優化的本構模型仿真結果仍與實驗結果存在差距。未來可以采取加工實驗和計算機優化協同作用的方式來優化本構模型，使模型仿真結果更加精確。