貝葉斯統(tǒng)計中單參數(shù)后驗分布的精確計算方法
黨 紅
(長治學院 數(shù)學系,山西 長治 046011)
1 引言
統(tǒng)計學界主要分為兩大學派:經(jīng)典統(tǒng)計學派和貝葉斯統(tǒng)計學派,兩者的主要區(qū)別在于是否利用先驗信息,主要分歧在于是否把總體中的未知參數(shù)看作是一個隨機變量。
近年來,貝葉斯統(tǒng)計思想在不同的領(lǐng)域都得到了廣泛的應(yīng)用,2017年薛玲余研究了貝葉斯估計在教育學中的應(yīng)用[1],2017年鐘建軍等研究了貝葉斯統(tǒng)計在心理學上的應(yīng)用[2],2018年張翠玲,譚鐵君研究了基于貝葉斯統(tǒng)計推理的法庭證據(jù)評價[3],2012年王彩鳳等研究了中國股市量價關(guān)系分析中的后驗分布構(gòu)造與模擬[4]。貝葉斯統(tǒng)計中一切統(tǒng)計推斷都是基于后驗分布來進行的,所以后驗分布的重要性不言而喻。
2 后驗分布的計算方法
2.1 直接計算后驗分布
在一個單參數(shù)貝葉斯統(tǒng)計問題中,設(shè)X~p(x|θ),在獲得樣本X后,參數(shù)θ的后驗分布即為給定X=x條件下θ的條件分布,記為π(θ|x)
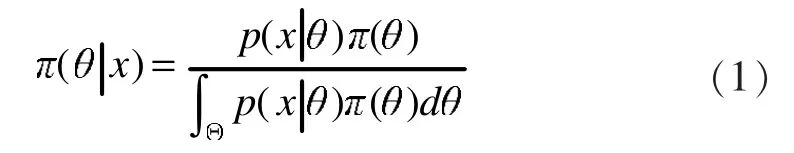
其中,p(x|θ)為樣本 X 對應(yīng)的總體分布,π(θ)為參數(shù)的先驗分布。
當已獲得樣本為X1,X2,…Xn時,可以利用似然函數(shù) L(x|θ)代替(1)式中的總體分布 p(x|θ)來計算后驗分布,即
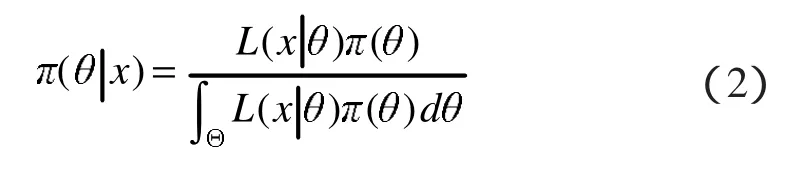
例 1 設(shè) X|θ~B(n,θ),參數(shù) θ服從均勻分布 U(0,1),求參數(shù) θ的后驗分布[5]。
解:因為 X|θ~B(n,θ),則其概率分布為
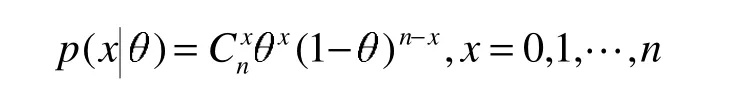
參數(shù) θ的先驗分布為 π(θ)=1,θ∈(0,1),故由后驗分布
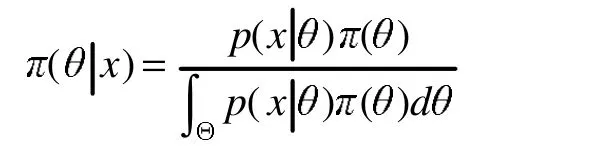
得到
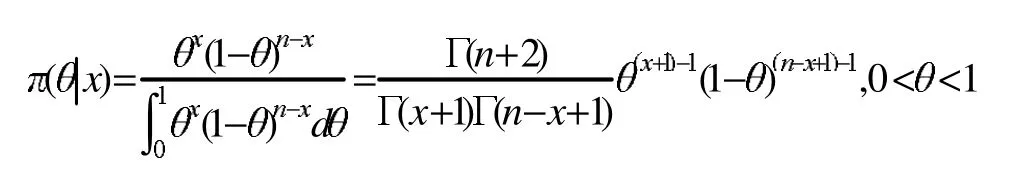
即,參數(shù)θ的后驗分布為貝塔分布Be(x+1,n-x+1)
2.2 由后驗分布的核計算后驗分布
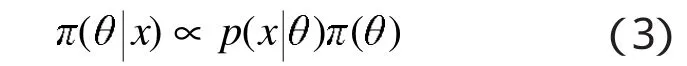
式(3)中,p(x|θ)π(θ)即可作為后驗分布 π(θ|x)的核,左端和右端兩式相差一個與參數(shù)θ無關(guān)的常數(shù)因子,將 p(x|θ)π(θ)正則化即可得到后驗分布。
例 2 設(shè) X|θ~N(θ,σ2),其中 σ2已知而 θ未知,參數(shù) θ的先驗分布為 N(μ,τ2),其中 μ 和 τ已知,求參數(shù)θ的后驗分布[5]。
解:因為 X|θ~N(θ,σ2),則其概率密度為
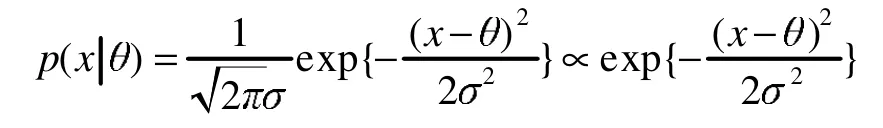
參數(shù)θ的先驗密度為
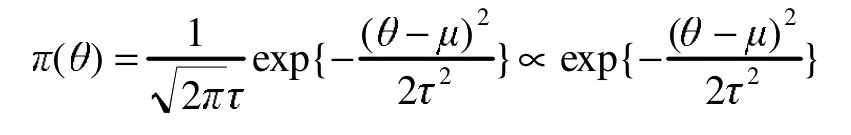
則參數(shù)θ的后驗密度
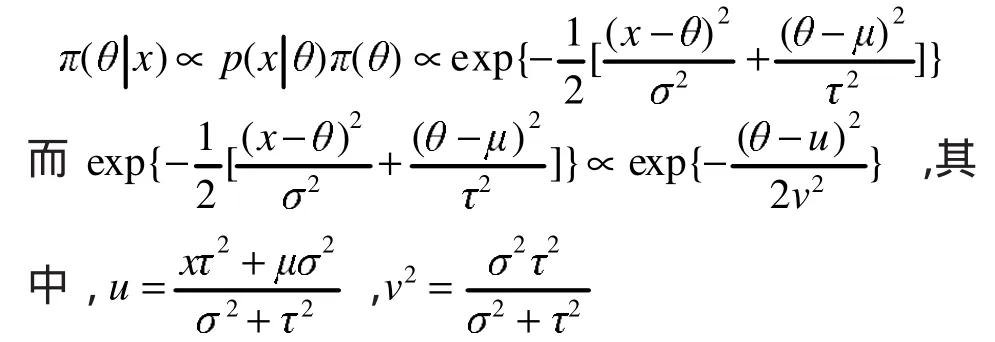
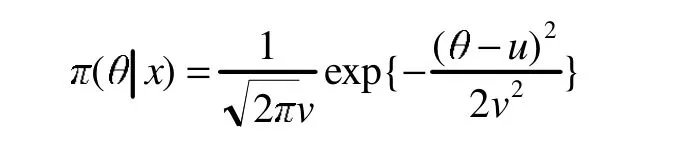
然而,常見的統(tǒng)計分布是非常有限的,式(3)中后驗分布的核在針對較為常見的分布時才便于計算。
上述兩種方法是僅有的針對單參數(shù)貝葉斯統(tǒng)計模型的精確后驗分布的計算方法。由于常見的分布十分有限,精確計算方法在實際應(yīng)用過程中具有局限性,這也是精確計算方法的主要缺點。
3 結(jié)束語
文章旨在為后驗分布在實際應(yīng)用中的計算提供理論基礎(chǔ),如果對后驗分布計算中的要求精度不高的話,在后驗分布計算方面還可以用利用R軟件[6]、SPSS軟件或Matlab軟件做輔助工具,更有利于簡化貝葉斯統(tǒng)計中后驗分布的計算,這也是后續(xù)研究過程中需要注意的方向。

