智能RGV的動態調度策略

賈武艷，王慧蓉

（長治學院 數學系，山西 長治 046011）

1 引言

RGV（Rail Guided Vehicle，有軌制導車輛）是一種無人駕駛、能在固定軌道上自由運行的智能車。它能根據指令自動控制移動方向和距離，并自帶一個機械手臂、兩只機械手爪和物料清洗槽，能夠完成上下料及清洗物料等作業任務。可有效提高了加工效率，在智能加工系統中起著重要的作用。具體智能加工系統的示意圖如圖1。

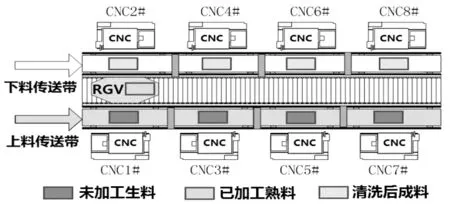
圖1 智能加工系統示意圖

2 動態任務調度問題

2.1 要解決的問題

（1）在每臺CNC上安裝同樣的刀具，只有一道工序的物料可以在任意一臺CNC上加工完成，在一班次的連續作業八小時下，生產出多少成料？

（2）在完成第一道、第二道工序的CNC上分別安裝不同的刀具，每個物料的第一和第二道工序分別由兩臺不同的CNC依次加工完成，在一班次的連續作業八小時下，生產出多少成料？

針對上述兩個具體問題給出兩各不同條件：一是寫出RVG動態調度模型和求解相應的算法；二是在CNC在加工過程中會發生概率大約為1%的故障的情況下，給出以下兩種情況的RGV動態調度模型和求解相應的算法。

2.2 模型假設

①假設題目給出的CNC工作時間是有效的、合理的；

②假設加工所有物料的速度是均勻的，恒定的；

③假設傳送帶運行速度很快，可忽略不計；

④假設每個CNC只能運輸一件物料；

⑤假設CNC在加工物料過程發生故障時，故障不會發生在首輪上料過程中。

1.3 符號說明

xi是 RGV移動個單位所需的時間（i=1，2，3）；

m是CNC加工完成一道工序的物料所需的時間；

n是CNC加工完成一個兩道工序的第一道工序所需的時間；

l是CNC加工完成一個兩道工序的第二道工序所需的時間；

y是RGV為CNCj一次上下料所需時間（j=1，3，5，7）；

z是RGV為CNCk一次上下料所需時間（k=2，4，6，8）；

w是RGV完成一次物料的清洗作業所需時間；

a是循環一次時，RGV移動1個單位的次數；

b是循環一次時，RGV移動2個單位的次數；

c是循環一次時，RGV移動c個單位的次數；

t為首次上料結束后，循環過程中相鄰兩次到達第一個上料位置的時間。

3 模型的建立與求解[1-3]

3.1 模型一的建立與求解

3.1.1 一道工序的物料加工作業的優化模型分析

（1）模型分析

①在協作時間內，RGV在一次循環中，路徑最短時方為最優。

②在循環中，8個CNC必須協作工作，即首次上料時，8個CNC均要上料。因此，無論怎么上料，上料時RGV所走的路徑必須大于6個單位距離。

③8個CNC上料完成，途中需停留6次，RGV每運行一次均要停留一次。

④如果RGV在進行完一次循環，每個CNC均未發出需求或下料信號時，RGV處于等待狀態。直到信號出現時，RGV進行智能操作。

（2）運行路徑

①上料階段：在每個CNC空閑時，先進行隨機上料，直到8個CNC均處于工作狀態，回到第一個上料的CNC前，等待。

②循環階段：開始按照上料的順序依次下料上料。

（3）具體符號表示

假設t表示首次上料結束后，循環過程中相鄰兩次到達第一個上料位置的時間。那么，如果t＜m+y時，則需要等待m+y-t秒；如果t≥m+y時，則在RGV到達第一個上料位置時，該CNC已在等待。

3.1.2 模型一的求解

RGV循環一次的清洗時間：t1=8 w；

RGV循環一次的上下料時間：t2=4（y+z）；

循環一次RGV移動所需要的時間：t3=ax1+bx2+cx3；

循環過程中，RGV到達初始位置的時間：t1+t2+t3；

根據上述分析建立線性規劃模型來求解一道工序的物料加工作業的最優值。建立模型如下：

目標函數：tmin=t1+t2+t3

決策變量：a，b，c

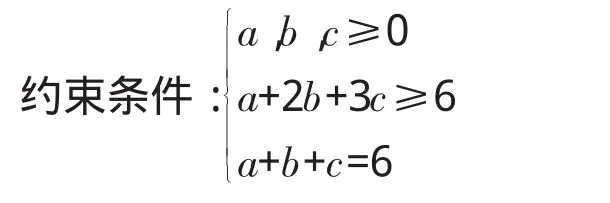
8小時中能加工物料的個數為

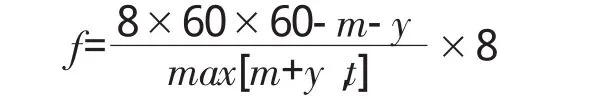
當max[m+y，t]取到最小時，f最大，即8小時中加工物料的個數最多，利用MATLAB軟件求得最優結果。

3.2 模型二的建立與求解

3.2.1 兩道工序的物料加工作業的優化模型的分析

（1）問題分析

①（設計CNC方面）：因為該物料需要兩步才可完成，所以需要考慮各個CNC負責的相應工序。

②（運行過程）：即在設置好CNC分別負責哪道工序后，使得RGV進行隨機上料，而后循環，使得RGV運行的總路徑最短。此時為最優解。

③只有設計最優和運行最優時，在8小時內生產物料最多。

（2）分析結果

（設計最優）CNC1#，CNC3#，CNC5#，CNC7#負責第一道工序。

CNC8#，CNC6#，CNC4#，CNC2#負責第二道工序。

（路徑最優）（其中給 CNC i上料記為 A（i），給CNC i下料記為 a（i），當然，除了第一次上料外，以后的上下料同時進行）

第一階段（上料過程） A（1）-A（3）-A（5）-A（7）-等待一段時間。

第二階段（循環過程）-a（1）-A（2）-a（3）-A（4）-a（5）-A（6）-a（7）-A（8）-等待一段時間或直接上下料。

3.2.2 模型二的求解

RGV循環一次的清洗時間：t1=4 w；

RGV循環一次的上下料時間：t2=4（y+z）；

循環一次RGV移動所需要的時間：t3=3x1+x3；

循環過程中，RGV到達初始位置的時間：t=t1+t2+t3；其中，t越小，模型越優。

8個小時加工兩道工序物料的個數：

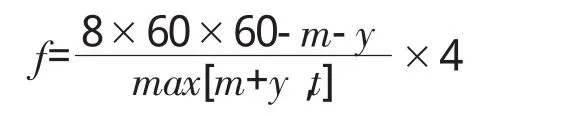
3.3 模型三的建立與求解

3.3.1 一道工序的物料加工作業且考慮故障時的優化模型的分析

由模型一可知，當加工只有一道工序的物料時，沿路徑 CNC1#，CNC3#，CNC5#，CNC7#，CNC8#，CNC6#，CNC4#，CNC2#的順序加工時RGV運行總路徑最短。其中每個CNC均可加工。運行示意圖如下：（其中給 CNC i上料記為 A（i），給 CNC i下料記為a（i），當然，除了第一次上料外，以后的上下料同時進行）

第一階段：（上料過程）A（1）-A（3）-A（5）-A（7）-A（8）-A（6）-A（4）-A（2）-等待一段時間。

第二階段：（循環過程）a（1）-a（3）-a（5）-a（7）-a（8）-a（6）-a（4）-a（2）

模型分析如下。

①優化：假設故障不會發生在上料過程中。

②故障出現在循環中的任意一段中，而實際上CNC中時刻有物料，故每次故障均有8個作廢。

③因為故障發生的概率為0.01，所以每加工100次平均有1次故障，而每個CNC每次加工一個物料。

④每次故障發生時均要維修并重新依次上料。

3.3.2 模型三的求解

在8小時只加工一道程序物料能加工數目：x；

在8小時只加工一道程序物料時出現故障次數：0.01x；

由于出現故障廢掉的時間：0.01（600+x+y）～0.01（1200+x+y）秒；

RGV循環一次的清洗時間：t1=8w；

RGV循環一次的上下料時間：t2=4（y+z）；

循環一次RGV移動所需要的時間：t3=6x1；

循環過程中，RGV到達初始位置的時間：t=t1+t2+t3；其中，t越小，模型越優化，可得結果如下：

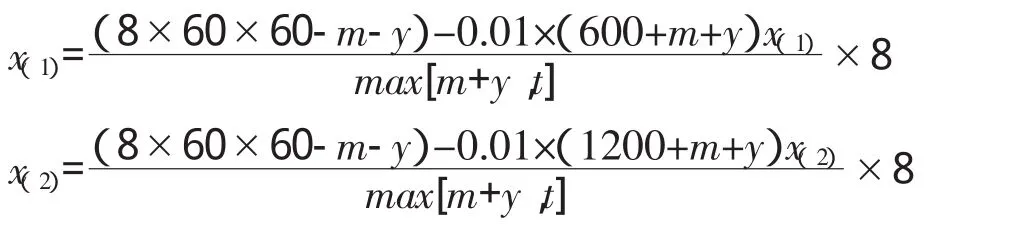
所以8小時能加工的物料數目范圍為x2≤x≤x1。

3.4 模型四的建立與求解

3.4.1 兩道工序的物料加工作業且考慮故障時的優化模型的分析

由模型二可知：當只加工兩道工序的物料時，沿以下順序加工時RGV運行總路徑最短。其中CNC1#，CNC3#，CNC5#，CNC7#加工第一道工序，CNC8#，CNC6#，CNC4#，CNC2#加工第二道工序。運行示意圖如下：（其中給CNC i上料記為A（i），給CNC i下料記為 a（i），當然，除了第一次上料外，以后的上下料同時進行）

第一階段：（上料過程）A（1）-A（3）-A（5）-A（7）-等待一段時間。

第二階段：（循環過程）a（1）-A（2）-a（3）-A（4）-a（5）-A（6）-a（7）-A（8）-

模型分析如下。

①優化：假設故障不會發生在上料過程中。

②故障出現在循環中的任意一段中，而實際上CNC中時刻有物料，故每次故障均有4個作廢。

③因為故障發生的概率為0.01，所以每加工50個均有8個CNC工作100次，平均有1次故障，而每個CNC每次加工一個物料中一個工序。

④每次故障發生時均要維修并重新依次上料。

3.4.2 模型四的求解

在8小時只加工兩道程序物料能加工數目：x

在8小時只加工一道程序物料時出現故障次數：0.02x。

由于出現故障廢掉的時間：0.02x（600+x+y）～0.02x（1200+x+y）秒

RGV循環一次的清洗時間：t1=4w；

RGV循環一次的上下料時間：t2=4（y+z）；

循環一次RGV移動所需要的時間：t3=3x1+x3；

循環過程中，RGV到達初始位置的時間：t=t1+t2+t3，其中，越小，模型越優化可得結果如下，

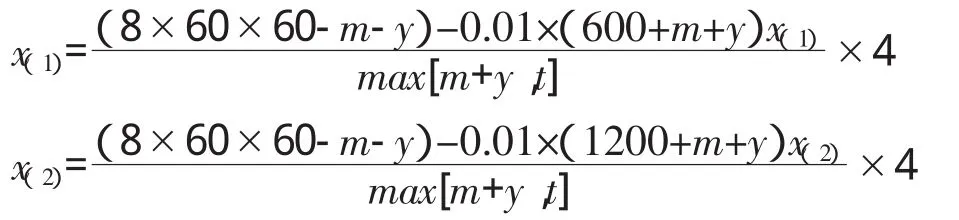
所以，8小時能加工的物料數目范圍為 x（2）≤x≤x（1）。

4 模型的評價[3]

4.1 模型的優點

（1）模型二是模型一優化之后的結果，更符合實際情形；

（2）運用MATLAB編程實現模型求解，使得求解結果更加精確，減少了人為因素帶來的誤差；

（3）建立的模型能與實際結合起來，結合實際問題求解，使得模型具有很好的通用性與推廣性。

4.2 模型的缺點

（1）模型不考慮傳輸帶的速度，而實際生產中必須考慮；

（2）模型沒有考慮RGV的清洗時間，而在實際生產中，熟料在清洗槽中需短暫停留，只不過是遠小于機械手將成料放到下料傳送帶上的時間，這點需要考慮。