無線傳感器網絡中基于自適應網格的多目標定位算法

王天荊，李秀琴，白光偉，沈航

（南京工業大學計算機科學與技術學院，江蘇 南京 211816）

1 引言

近年來，基于無線傳感器網絡（WSN, wireless sensor network）的多目標定位技術已被廣泛應用于機器人導航、地理路由、公共安全、環境監測、車輛跟蹤等多個領域[1-5]，其中，高精度、高效率的定位算法一直是研究熱點之一。傳統的多目標定位算法可分為基于測距和基于非測距兩類，前者需要節點有測距功能，主要有基于到達時間[6]、基于到達時間差[7]等定位算法；后者通過網絡的連通性實現多目標定位，主要有加權質心定位算法[8]、修正權值網格質心定位算法[9]等。上述算法雖簡單易行，但需要額外的輔助設備，且定位精度易受到復雜環境下無線電波波動的干擾。為了不增加硬件設施成本，基于接收信號強度(RSS, received signal strength)的多目標定位技術根據傳感器節點可以獨立測量接收信號強度的特性，通過檢測監測區域內RSS來確定目標位置。文獻[10]在離線階段使用核函數特征提取方法獲得 RSS 信號特征，構成位置指紋空間；在線定位階段采集在線位置指紋數據，利用改進的加權k近鄰算法匹配位置指紋空間中的數據，估計待測目標位置。但是，基于位置指紋的定位技術需要對大量的數據進行測量、處理和存儲，然而傳感器節點的能量、內存和通信能力均受限。不同于RSS定位技術，文獻[11]提出的語義目標定位算法通過節點間大量的信息交互來探知監測環境，再利用環境信息估計目標位置。這兩類方法中大量信息的傳遞消耗了有限的網絡資源，因此減少數據傳輸和資源消耗是多目標定位亟待解決的問題之一。

近年來，興起的壓縮感知（CS, compressive sensing）技術[12]為多目標定位帶來了新的機遇。WSN中的多目標定位問題具有天然的稀疏性，因此可以利用CS理論大幅減少節點采樣的數據量，減少資源消耗。文獻[13]將WSN的監測區域離散成若干個網格，并依據CS理論將多目標定位問題轉化成一個K-稀疏信號的重構問題，由sink節點利用l1最優化從觀測向量中重構出目標位置。文獻[14]以目標節點與錨節點連通度為觀測值，運用最小化l1范數法，通過高計算量的梯度下降法求解目標位置。針對l1最優化重構算法計算復雜度高的問題，文獻[15]利用貪婪匹配追蹤（GMP, greedy matching pursuit）算法實現多目標定位，但該算法的定位誤差需要進一步改善。文獻[16]改進了GMP算法，提出使用貪婪匹配殘差優化算法重構K-稀疏信號，提高了定位精度。基于貪婪法的定位算法雖計算復雜度低，但需要信號的稀疏度作為先驗條件，即需要預知目標個數。然而，實際應用中節點不僅無法獲知目標個數，而且無法確定滿足CS重構條件所需的采樣數據量。因此，如何確定最優觀測次數以克服因采樣數據量未知而導致的不充分采樣或過度采樣問題，是多目標定位的挑戰之一。

通常，基于CS的定位方法用固定網格劃分監測區域[14-17]。為了保證辨識出每個目標的位置，只能將網格劃分得十分細小，這大大增加了最優化模型的規模及重構算法的計算復雜度，從而存在加大定位誤差的風險。為了解決此問題，文獻[17]提出了一種基于稀疏貝葉斯學習的網格自適應多源定位算法，該算法設計的自適應網格能使定位誤差低于固定網格劃分下定位誤差的理論下界。文獻[18]提出了一種兩階段的目標定位算法：在粗定位階段利用l1最優化重構出目標的初始候選網格；在細定位階段依次四分每個初始候選網格，在越來越小的子網格內確定目標的精確位置。上述定位算法雖解決了在大范圍內以高計算代價估計目標位置的問題，但在細定位時依然要求所有節點傳輸感知數據至sink，這種集中式的定位方法易使節點因通信量大而過早失效，從而導致網絡拓撲的不穩定性。根據目標在監測區域內的稀疏性，如何建立分布式的多目標定位方法是熱點問題之一。

針對以上問題，本文提出了一種基于自適應網格的多目標定位算法，該算法分為2個階段：在大尺度網格定位階段，采用序貫壓縮感知（SCS,sequential compressed sensing）原理選擇最優觀測次數，通過lp最優化重構出目標所在的初始網格位置；在小尺度網格定位階段，根據CS重構要求自適應劃分目標所在的初始網格，再次采用SCS原理選擇最優觀測次數，通過lp最優化確定目標在初始網格中的精確位置。本文主要貢獻如下。

1) 基于大尺度網格的定位方法在監測區域內區分目標存在和不存在的子區域；基于小尺度網格的定位方法在目標存在的子區域估計目標的位置，使目標定位更有針對性和高效性。

2) 利用 SCS數據采集方法和lp最優化稀疏重構方法共同減少節點的觀測數據量，從而大大降低網絡資源開銷。

3) 實驗仿真結果表明，與傳統的基于CS的多目標定位算法相比，在保證定位精度的同時，本文算法所需的觀測次數大大減少，定位的時間開銷顯著降低。

2 相關背景及準備工作

2.1 壓縮感知

CS技術可用遠低于奈奎斯特采樣率(Nyquist sampling frequency)的速率對K-稀疏信號進行采樣，并利用如式(1)所示的l0最優化問題重構出K-稀疏信號*

x。

其中，觀測矩陣P滿足有限等距性質（RIP, restricted isometry property）[19]。正交匹配追蹤算法（OMP, orthogonal matching pursuit）[20]、分段正交匹配追蹤算法（StOMP, stagewise orthogonal matching pursuit）[21]等貪婪算法都可求解式(1)問題，但是它們均需要信號稀疏度作為先驗條件，且重構誤差較大。于是，文獻[22]將l0最優化問題松弛為l1最優化問題，如式(2)所示。

式(2)所示的問題可由梯度投影法（GPM, gradient projection method）、基追蹤算法（BP, basis pursuit）[23]、子空間追蹤算法（SP, subspace pursuit）[24]、迭代收縮閾值法（ISTA, iterative shrinkage-thresholding algorithm）等求解，但易于收斂到次優稀疏解，且計算復雜度高。

2.2 CS定位問題描述

假設在WSN監測區域內隨機部署了M個位置已知的傳感器節點和K個位置未知的目標，則基于CS的多目標定位系統將此區域離散為N(N=n×n)個網格，并設每個目標只出現在某個網格的中心位置，如圖1所示。

不妨定義K個目標的位置向量為x=(x1, … ,xN)，其中，若第j個網格存在目標，則xj=1，否則xj= 0 。根據強度-距離損耗模型[25]，第i個節點在理想情況下接收到第j個網格中目標發出的RSS值為其中，pt表示在參考距離d0處的接收信號強度，dij為第i個節點與第j個目標之間的歐式距離，路徑衰減指數η一般為 2～5。監測區域內M個節點采用觀測矩陣獲得觀測向量y=Px，并將之傳輸給sink；接收到y后，sink可以由觀測信息重構出K-稀疏向量x*來估計目標的位置，因為x*中非零元素的位置對應著K個目標在N個網格中的位置。

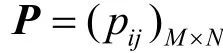
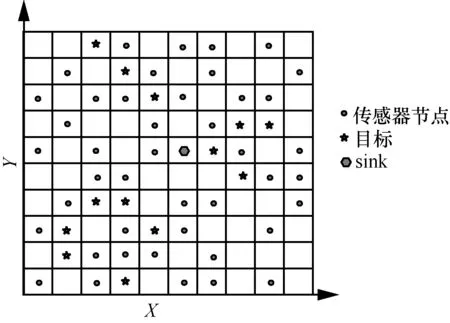
圖1 基于CS的多目標定位系統模型

傳統的基于CS的定位方法主要利用l0最優化或l1最優化來重構目標位置，很少考慮利用lp(0 ＜p＜ 1 )最優化[26]完成定位任務；而lp范數對向量稀疏性的度量優于l0范數和l1范數，因此本文通過求解如式(4)所示的lp(0 ＜p＜ 1 )最優化問題實現多目標定位。

充分的觀測數據量是求解問題式(4)的前提條件，然而在實際場景下，定位系統無法預知目標個數，即無法獲知向量x的稀疏度，因此無法確定重構所需的觀測次數。若觀測次數過多，對提高重構精度的貢獻有限，但增加了采樣成本；若觀測次數過少，則無法精確重構出*x。

2.3 基于SCS的最優采樣

SCS技術克服了因觀測數據量未知而導致的不充分或過度采樣問題，其基本思想是在初始m個觀測值上疊加T個觀測值，使以的概率得到的重構誤差滿足式(5)。

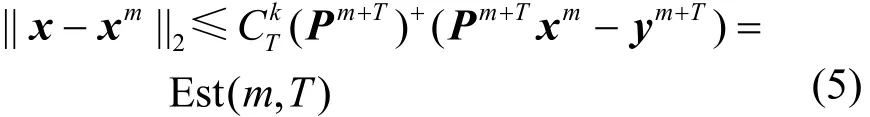
于是，當重構誤差的估計值Est(m,T)小于門限值τ時，停止接受新的觀測值；否則，以T為步長，序貫增加觀測次數直至Est(m,T)滿足門限要求，獲得最優觀測向量m+STy。

3 基于自適應網格的多目標定位算法

由上述討論可知監測區域的網格劃分影響著式(4)所示問題的求解。若網格劃分的尺度過小，則使式(4)所示問題中欠定線性方程組的規模急劇增加，從而大大增加重構算法的計算量，延長定位時間；若網格劃分的尺度過大，則一個網格中可能存在多個目標，定位時容易出現目標丟失。由此，設置合理的網格尺度可提高定位的準確性、及時性及降低系統的計算復雜度。通常，網格尺度的劃分依賴于目標的先驗信息，但WSN無法獲知這些信息。不過某些實際場景下多個目標會分別聚集在小區域內，如圖2所示。于是，本文分別采用大尺度網格劃分和小尺度網格劃分這2個階段實施多目標定位，具體過程如下。

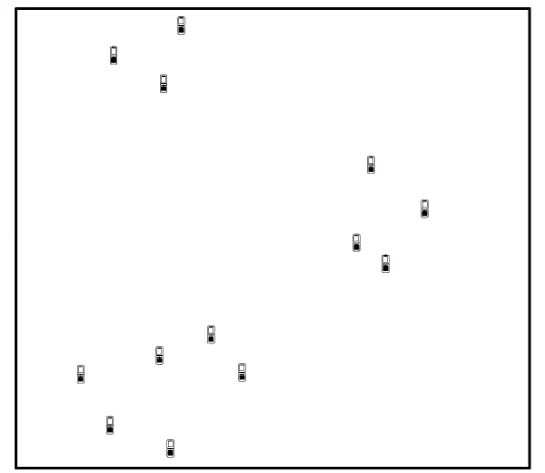
圖2 實際的多目標定位場景

3.1 大尺度網格定位

WSN啟動多目標定位任務時，為了減少感知開銷，首先用大尺度劃分監測區域，以確定存在目標的子區域，如圖3所示。假設面積為S=a0×a0的監測區域被劃分為N0=n0×n0個初始網格, 第i(i∈{ 1,…,N0})個初始網格的狀態向量定義為其中為初始網格的中心位置，或分別表示該初始網格中存在或不存在目標。根據SCS原理，在區域內隨機選擇m0+T0個節點進行目標感知，且將觀測值傳送給sink；sink計算重構誤差的估計值 E st(m0,T0)確定是否繼續接收新的觀測值，經過S0-1次的序貫接收，最終獲得最優觀測向量利用式(6)所示的l最優p化重構出稀疏向量

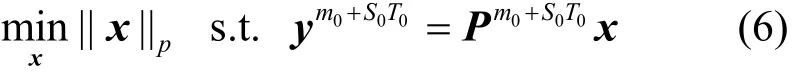
對預設的門限值γ，當時，說明第i個初始網格中可能存在著多個目標，且元素的幅值是多個目標位置信息的累加；反之，不存在目標，此時只需簇頭周期性地監測子區域，成員節點暫時休眠，以減少網絡資源開銷。

圖3 大尺度網格劃分下多目標定位模型

下面，本文重點對存在目標的K0個子區域進行基于自適應網格的目標定位。

3.2 自適應網格定位

為了在第i(i∈ {L1, … ,LK0})個初始網格中進一步確定目標的精確位置，需要自適應調整尺度來重新劃分初始網格，其中，子列 {L1, …,LK0} ? {1,…,N0}是存在目標的初始網格的序號。

因為此網格中目標個數未知，第一步假設只存在一個目標，記個數為由 CS原理可知，通常精確重構出稀疏解所需的觀測次數應至少滿足M=4K[27]，則劃分初始網格后的小尺度網格個數需滿足即（如圖 4(a)所示）。sink隨機激發初始網格中的個節點進行聚類和感知，成員節點將觀測值發送給簇頭。如果簇頭由SCS計算的估計值 E st(mi,Ti1)＜τ，則增加新的觀測值。如果每次固定增加T個觀測值，則由SCS無法較快地確定最終的觀測次數。為了快速分析出所需增加的觀測值，不妨定義比值如式(7)所示。

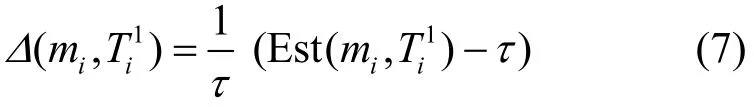
ii例如，在圖4(a)中計算得到Δ(mi,Ti1) ＞ 0 ，為了提高定位效率，需將初始網格重新劃分成個小網格，且需滿足圖 4(b)顯示3× 3的網格被劃分為5× 5，而非4×4的網格。由CS重構條件可知，使用3× 3的網格至多可識別出2個目標，即3× 3 ＞ 8 = 4 × 2 ；而使用5×5的網格至多可識別出6個目標，即5× 5 ＞ 2 4 = 4 × 6 。因CS中壓縮比不易過高，考慮5× 5 ＞ 1 6 = 4 × 4 。于是，簇頭新接收Ti2= 1 2個觀測值，總觀測次數為

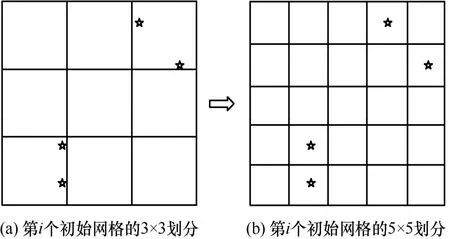
圖4 第i個初始網格的自適應劃分示意

第二步，簇頭計算重構誤差的估計值Est(m,T1+T2)，若此估計值仍大于τ，則重新劃

iii分網格且接收Ti3個觀測值；反之，則停止接收新的觀測值。簇頭由式(8)所示的lp最優化重構出稀疏向量

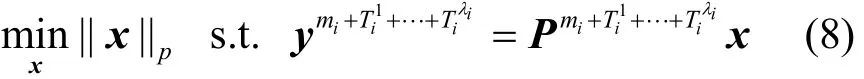
傳統的 CS定位方法一般采用集中式處理方式，消耗了大量的信道資源和傳輸開銷。同時，節點實時感知不存在目標的子區域會產生過多的感知開銷。本文設計的定位方法較好地解決了上述問題，初始階段基于大尺度網格的集中式定位方法在監測區域內區分目標存在和不存在的子區域，后續階段基于小尺度網格的分布式定位方法并行地對存在目標的多個子區域進行精細定位。這種全局與局部結合、集中式與分布式結合及粗定位與細定位結合的方式為高精度、高效率的多目標定位提供了一種新的思路，更易應用于現行的分層結構的WSN，并推廣至不同場景下的多目標定位問題。

根據上述討論，本文提出的基于自適應網格的多目標定位算法的流程如圖5所示。

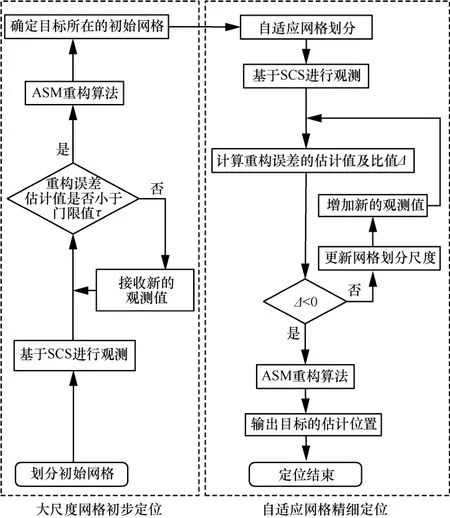
圖5 基于自適應網格的多目標定位算法流程

3.3 初始網格的合并與定位

初始階段，sink由重構向量x0確定了每個初始網格的狀態向量并獲得了位置向量ID0= (L1, … ,LK0)，其中，所在的網格位置序號。如前文所述，監測子區域內聚集著多個目標，所以不難發現ID0中目標所在的初始網格常常相互鄰近。如果聯合這些相鄰網格一起進行基于自適應網格的細定位，相比于單個初始網格各自進行定位可以大大減少感知、傳輸和計算開銷。

如圖6所示，大尺度網格定位將監測區域劃分為N0= 5× 5 個初始網格，并確定了存在目標的初始網格，其中存在3種初始網格相鄰情況。下面分別討論合并初始網格后的自適應網格定位方法。

Case 1 3個初始網格相鄰。將圖6 (a)中c1區域擴展為4個初始網格且假設目標個數為首先，由SCS將子區域劃分為個小網格，并在子區域及周圍隨機選擇個節點進行觀測，計算估計值及比值此時有需要接收較多的觀測值。于是將子區域重新劃分為個小網格，獲取新的次觀測。然后，簇頭重新計算估計值及比值此時有簇頭從觀測向量中由最優化重構出稀疏向量個非零系數所在的網格中心即為個目標的估計位置，坐標為其中

圖6 合并且自適應劃分目標所在的相鄰初始網格

Case 2 2個初始網格直接相鄰。將圖6(a)中c2區域擴展為 2個初始網格且假設目標個數為首先，由SCS將子區域內每個初始網格劃分為3× 3個小網格，共個小網格，并在子區域及周圍隨機選擇m+T1=8個節點進行觀測，計算估計c1c2值及 比值此 時有只需接收少量新的觀測值，取次觀測。然后，簇頭重新計算估計值及比值此時有不需要再接收新的觀測值。簇頭從觀測向量中由最優化重構出稀疏向量個非零系數所在的網格中心即為個目標的估計位置，坐標為

Case 3 2個初始網格對角相鄰。將圖6(a)中c3區域擴展為 4個初始網格且假設目標個數為首先，由SCS將子區域劃分為個小網格，并在子區域及周圍隨機選擇個節點進行觀測，計算估計值和比值此時時，需要接收較多的觀測值，于是將子區域重新劃分成個小網格, 再接收次觀測。然后，簇頭計算估計值和比值此時有簇頭從觀測向量中由最優化重構出稀疏向量其中，個非零系數所在的網格中心即為個目標的估計位置，坐標記為

4 實驗仿真及結果分析

下面對本文提出的WSN中基于自適應網格的多目標定位算法進行仿真實驗，主要分為兩部分：首先，分別與基于CS的多目標定位算法和基于兩階段的多目標定位算法進行對比，驗證本文算法具有更優的定位性能；然后，對比不合并和合并初始網格的定位性能，驗證合并初始網格的高效性。

4.1 仿真場景

在Matlab中進行仿真實驗。假設在正方形監測區域內隨機高密度部署大量的傳感器節點，K個待定位的目標隨機分布在區域內的任意位置。參照文獻[18]，仿真參數的設置如表1所示。

表1 仿真參數設置

為了評估定位性能，定義多目標定位誤差為

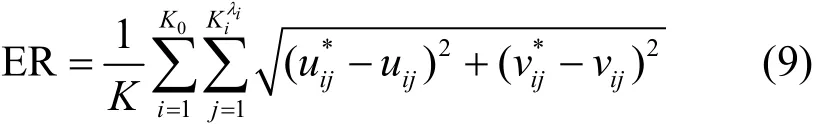
其中，tcen為大尺度網格劃分下的定位時間，tdis為小尺度網格劃分下的定位時間；若ti為自適應劃分第i個初始網格的定位時間，則tdis=max{t1, … ,ti,…,tK0}。

4.2 基于自適應網格的多目標定位算法的性能分析

4.2.1 大尺度網格的定位性能分析

WSN啟動多目標定位后，大尺度網格的設置影響著后續自適應網格的設置。下面實驗分析不同的大尺度網格劃分對定位性能的影響。將K=7個目標和M=50個節點隨機部署在不同面積的監測區域內，定義平均定位時間作為評估指標，其中，Nt= 5 0表示蒙特卡洛實驗的次數，TIi為第i次實驗的多目標定位時間。

針對不同的大網格尺度劃分，圖7顯示不同監測區域面積下平均定位時間隨著網格尺度變小而減小，但當初始網格數量達到一定規模時，平均定位時間又會增加。這是因為初始網格尺度設置過大時，自適應網格定位階段會進行多次網格細劃分操作，增加了計算時間；而初始網格尺度設置過小，存在目標的初始網格就過多，增加了自適應網格定位的計算時間。可以看出，4種監測區域面積對應的最佳大網格劃分分別為8× 8、9×9、9×9、10× 10，則網格劃分尺度n0與監測區域邊長a0比值分別約為 16%、13%、10%、9%，因此可以按照8%～18%比例來確定大網格的尺度。

4.2.2 對比基于CS的多目標定位算法

在上述實驗的基礎上，本文分析了50 m×50 m的監測區域內不同CS定位算法的性能。傳統的基于CS的定位算法直接將監測區域細劃分成20×20的網格，應用BP算法、OMP算法或GMP算法對K個目標進行定位，而本文算法在8× 8的初始網格劃分下實施自適應網格定位，估計K個目標的精確位置。定義平均定位誤差來評估不同定位算法的定位性能。

圖7 不同監測區域面積下平均定位時間與初始網格規模的關系

由圖8(a)可知，隨著目標個數的增加，本文算法均獲得了最佳定位結果，其平均定位誤差遠遠小于BP算法、OMP算法和GMP算法。例如，當K=8時，本文算法的定位精度比BP算法、OMP算法和GMP算法分別提高了85%、89.6%和83.6%。這不僅因為基于lp最優化的稀疏重構精度優于l0最優化和l1最優化，而且分為全局和局部2個階段定位目標比直接全局定位目標更精確、更符合實際場景。圖 8(b)顯示本文算法的平均定位時間少于 BP算法和GMP算法，雖高于OMP算法，但為了提高定位精度，可容忍增加37%的平均定位時間。圖8(c)顯示了感知節點個數隨著目標個數變化的情況，與其他3種算法相比，本文算法可大大減少感知節點個數，即重構所需的觀測次數。

圖9給出了K=7時4種算法的定位示意，可以看出，本文算法的定位準確性最高。利用BP算法、OMP算法和GMP算法重構稀疏解時，其非零元素的位置都出現了偏差，因而出現了漏檢目標和虛假目標的情況。

基于CS 的多目標定位易受環境的影響，為驗證本文算法的抗噪性能，將K=10個目標和M=60個傳感器節點隨機部署在監測區域內。圖10(a)顯示隨著信噪比的增加，節點接收的目標信號強度準確性顯著提高，因此4種定位算法的平均定位誤差均呈下降趨勢，其中，本文算法的定位精度明顯優于其他3種算法。當SNR從-6 dB變化到24 dB時，本文算法的平均定位誤差分別比BP算法、OMP算法和GMP算法最多降低了77.0%、82.5%、65.0%；當SNR大于20 dB時，本文算法的定位精度在0.5 m以內，而此時其他3種算法的定位精度分別在2 m、3 m和1.8 m以內。圖10(b)顯示隨著信噪比的增加，4種定位算法的平均定位時間均逐漸減少，本文算法的平均定位時間明顯小于BP算法和GMP算法，但大于OMP算法。為了提高定位精度，可以容忍一定程度上增加定位時間。因此，本文算法的抗噪性能優于傳統的CS定位算法。

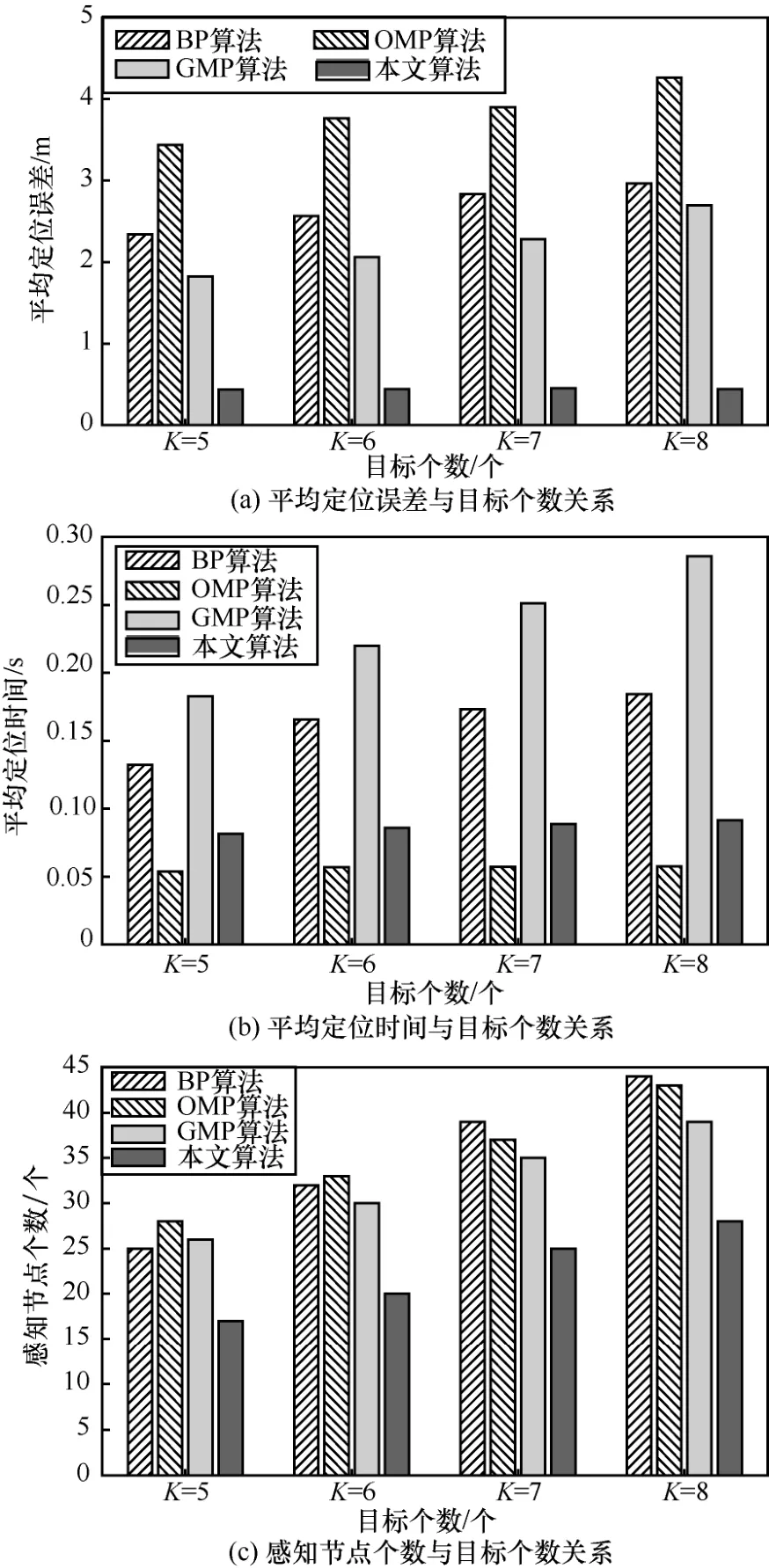
圖8 不同目標個數下4種定位算法的定位性能比較

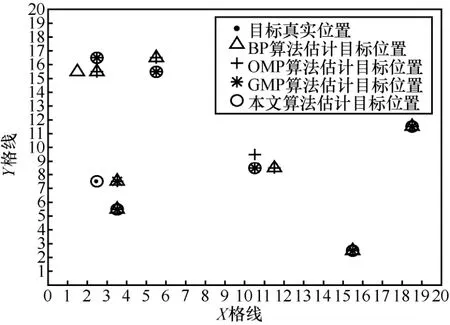
圖9 4種定位算法的多目標定位示意

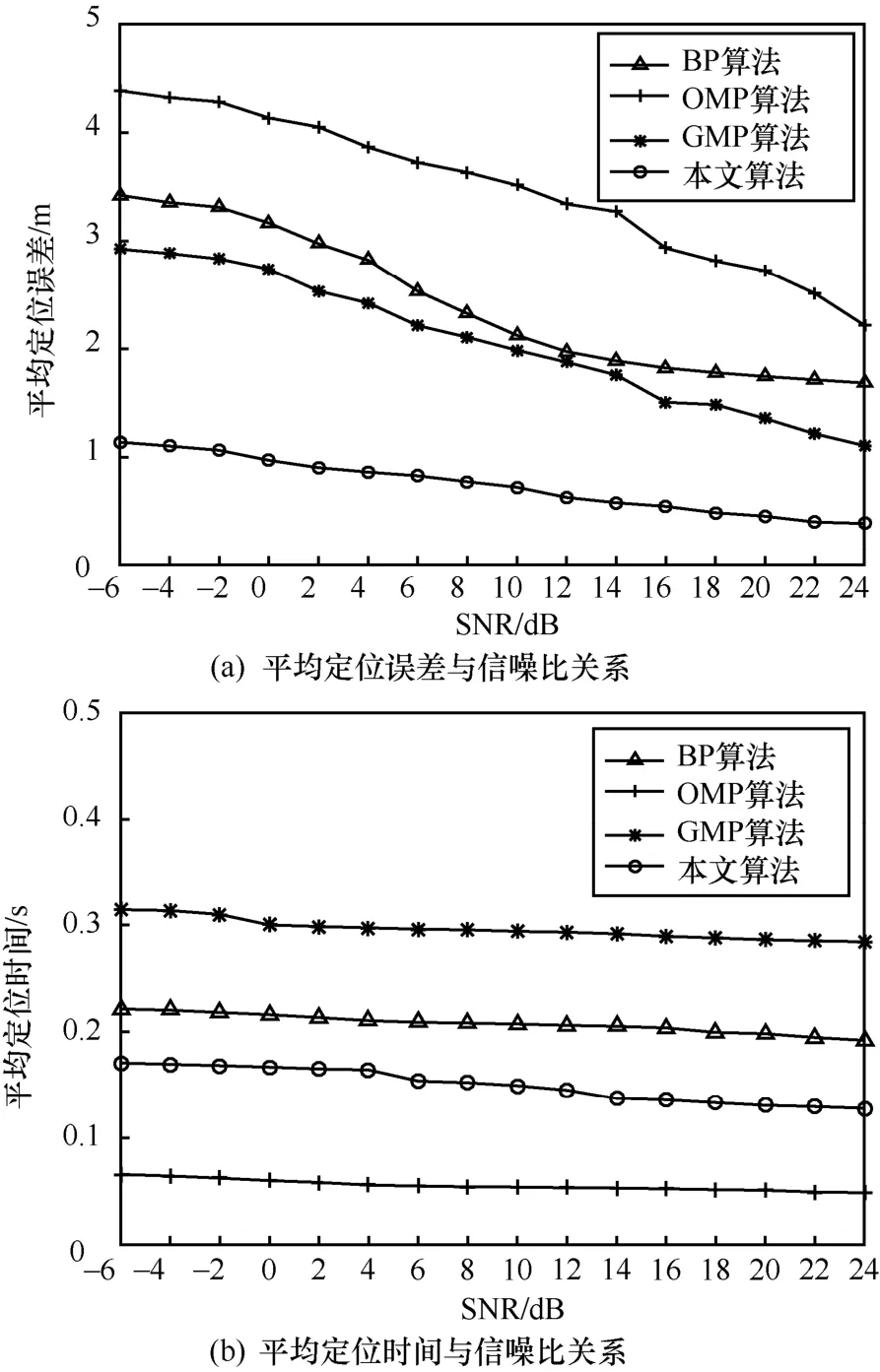
圖10 不同信噪比下4種定位算法的定位性能

隨著“萬物相連”的物聯網的廣泛應用，WSN作為其基礎設施，規模越來越大，因此傳統的多目標定位算法不再適用于大規模的 WSN。當監測區域面積不斷增加時，傳統的基于CS的定位算法劃分出的網格數量急劇增加，使重構算法的計算復雜度大大增加，從而影響了目標定位精度。例如，在K= 1 5，M=90，SNR=20 dB情況下，分別將50m× 50m、80m× 80m、100m× 100m、120m× 120m的監測區域劃分為20×20、25×25、30× 30、35× 35的網格。圖 11(a)顯示隨著監測區域面積的增加，BP算法、OMP算法和GMP算法的平均定位誤差均有大幅增長。然而，本文算法首先大尺度劃分監測區域，避免了在大范圍內以高計算代價重構目標位置，然后對存在目標的小區域進行自適應網格定位，大幅提高了定位精度，減少了平均定位時間，如圖 11(b)所示。例如，監測區域為120 m× 120 m時，本文算法的平均定位誤差比 BP算法、OMP算法和GMP算法分別降低了77.2%、81.8%和 87.2%；相應的平均定位時間分別減少了81.4%、56.2%和86.3%。

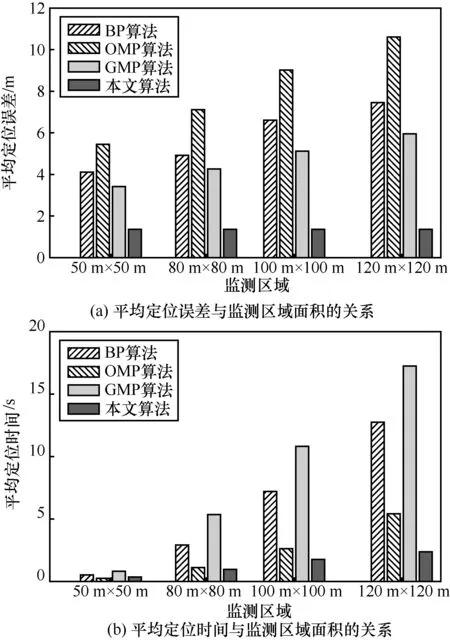
圖11 不同監測區域面積下4種定位算法定位性能比較

4.2.3 對比基于兩階段的多目標定位算法

為了提高定位精度，文獻[18]設計了基于兩階段的多目標定位算法（下文中稱為對比算法），該算法按次對每個候選網格進行多次四分操作來確定目標位置，花費較長的定位時間。本文算法并行地對所有存在目標的子區域進行自適應網格定位，大大減少了定位時間。下面的實驗比較了在50 m×50 m的監測區域內不同信噪比下 2種分階段定位算法的性能。圖 12(a)顯示隨著信噪比的增加，2種定位算法的平均定位誤差均逐漸減小，然而在所有 SNR下本文算法的平均定位誤差均遠遠小于對比算法，約減少了72%～88%。相應地，隨著信噪比的增加，圖12(b)中2種定位算法的平均定位時間均逐漸減少，但本文算法的平均定位時間比對比算法減少了約 83%～94%。當K=8， S NR為- 6 ～ - 2 dB時，本文算法的平均定位誤差比對比算法降低了 62%～60%，而平均定位時間比對比算法減少了90%～88%。因此在低SNR下本文算法仍然可以及時、精準地確定出多個目標的位置，為復雜無線環境下的多目標定位提供有力的保障。

目標個數的增加（即位置向量x的稀疏度降低）直接影響著從觀測向量中重構目標位置的性能，所以本文分析信噪比為5 dB和-5 dB下目標個數對定位結果的影響。在監測區域內隨機部署M= 9 0個傳感器，圖 13(a)顯示隨著目標個數的增加，2種分階段定位算法的平均定位誤差均逐漸增大，但本文算法的平均定位誤差遠遠小于對比算法，最多減少了 73%。同時，圖 13(b)顯示其平均定位時間也遠遠小于對比算法，最多減少了93%。這是因為對比算法按次對每個候選網格進行多次四分定位，隨著目標個數的增加，定位時間必然會大大增加。然而，本文算法對存在目標的初始網格并行地進行自適應網格定位，可大大減少定位時間。可見在目標個數較多時，本文算法具有更好的準確性、及時性。

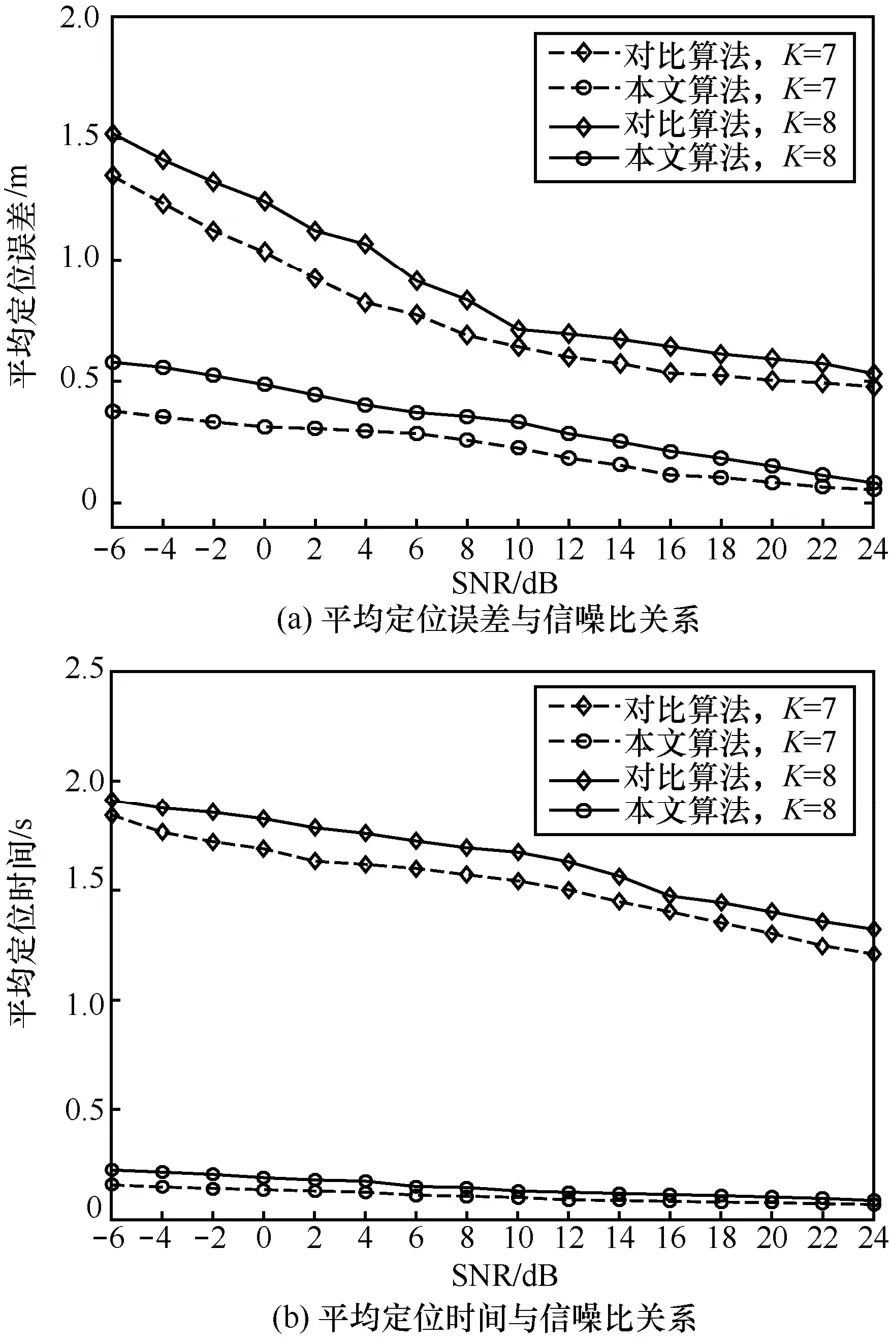
圖12 不同信噪比下2種分階段多目標定位算法的定位性能

4.3 自適應合并初始網格的性能分析

對每個初始網格進行自適應定位，必然使WSN出現較多的分簇，引起過多的資源開銷。如果將相鄰的初始網格合并，可以更高效地實現子區域的目標定位。為此，將K=10個目標隨機分布在圖14中40 m×40 m的監測區域內，并將之先劃分成6×6的網格。sink根據SCS收集m+3T= 3 0(m=6,T=8)個觀測值，利用lp最優化確定出存在目標的初始網格，并依據稀疏解中非零元素的位置合并初始網格，如圖14中黑色線框所示。自適應網格定位階段，表2顯示合并初始網格的定位方法比不合并初始網格的定位方法在定位時間上具有明顯優勢，而且當合并的初始網格個數越多，定位時間的減少越明顯。例如，c1區域合并 3個相鄰的初始網格后，其定位時間比不合并初始網格減少了71.5%。

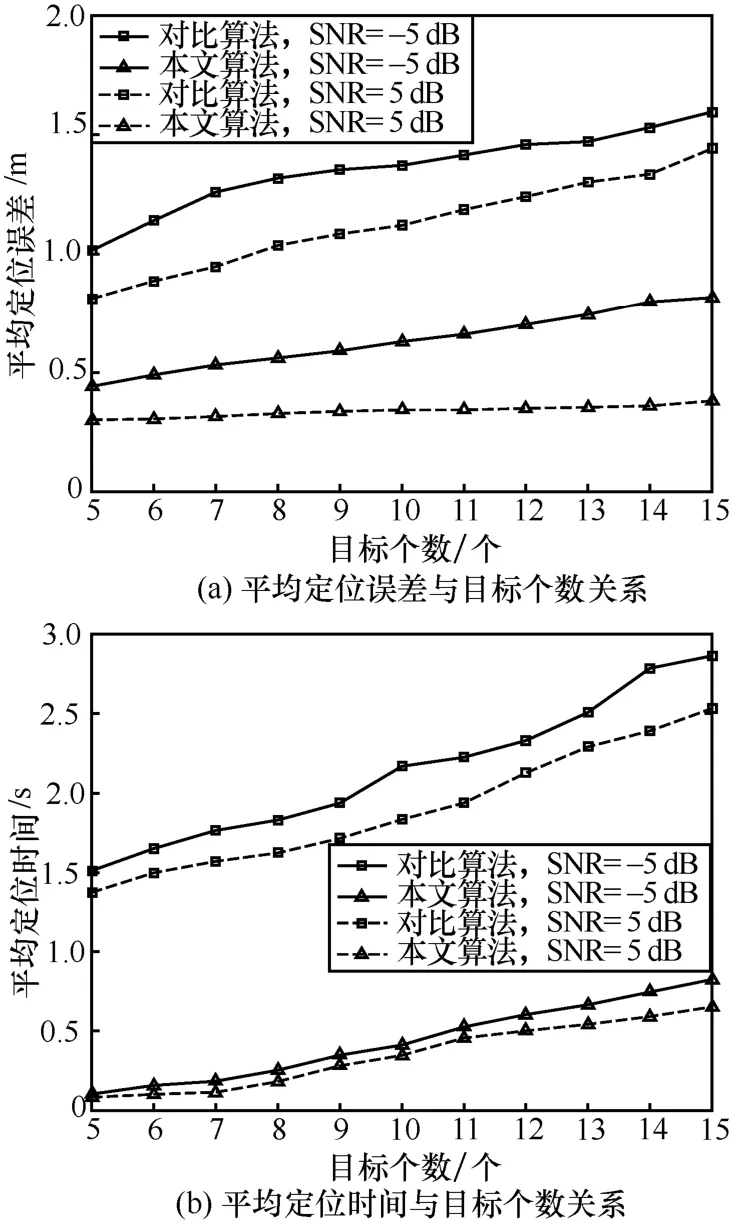
圖13 不同目標個數下2種分階段多目標定位算法的定位性能比較

圖14 自適應合并目標所在初始網格的實景

表2 2種小尺度網格定位方法的定位時間比較

5 結束語

本文提出了一種WSN中基于自適應網格的多目標定位算法，將大尺度網格確定目標大致位置與小尺度網格確定目標精確位置相結合。與傳統的基于CS的定位算法相比，本文算法減少了網絡的采樣開銷，且具有良好的抗噪性能。仿真實驗表明本文算法在保證定位精度的同時有效地降低了定位時間開銷。目前，尚沒有在OPNET或OMNET++等仿真平臺上進行實驗，因此對于本文算法在實際傳感器網絡中的驗證有待下一步解決。