采用結構仿生的重型機床立柱的綜合優化

李宇鵬 巴春來 劉來超

1.燕山大學機械工程學院，秦皇島，0660042.河北省重型智能制造裝備技術創新中心，秦皇島，0660043.中國汽車工程學會，北京，100055

0 引言

在提升重(大)型機床重型復雜構件的剛度、抗振性、可靠性基礎上，實現重型構件的輕量化和尺寸最佳化，是發展先進重型精密數控機床必然面臨的一項關鍵而迫切的課題[1]，目前常用的諸多單一優化方法難以滿足高精度、高可靠性重型機床的高剛度、高抗振性、輕量化、尺寸最佳等綜合需求。探究新的綜合優化方法以進行重型機床結構設計是發展的需求。蒲凡等[2]對機床立柱進行了靜特性分析及拓撲優化，賽宗勝等[3]用有限元分析找到了機床立柱的薄弱環節并對關鍵尺寸進行了優化。然而，單一優化存在諸多局限性，難以實現多項性能指標的綜合提升。本文以球形蝸桿砂輪磨齒機立柱為研究對象，探討拓撲優化、結構仿生優化、尺寸優化的綜合應用。

1 球形蝸桿砂輪磨齒機

球形蝸桿砂輪磨齒原理源于球形蝸桿與內齒輪的嚙合。磨齒機有5種基本運動：立柱(旋轉型)展成轉動ωC、工作臺展成轉動ωD1、工作臺差動轉動ωD2、砂輪軸轉動ωE、砂輪架移動vE，圖1為磨齒機的原理圖。砂輪軸線與內齒圈軸線成一空間夾角，砂輪法剖面“當量齒輪”與內齒圈的嚙合運動展成出齒廓包絡線[4]。砂輪沿內齒圈的徑向進給實現磨削齒圈的全齒高；砂輪沿內齒圈的軸向進給實現磨削齒圈的全齒長。

C—旋轉型立柱部件 D—組合工作臺部件 E—砂輪架部件圖1 球形蝸桿砂輪磨齒機原理圖Fig.1 Principle diagram of gear grinding machine

球形蝸桿砂輪磨齒機總體結構見圖2a[5]，用連續分度展成法加工分度圓直徑3～6 m、模數10～40 mm的硬齒面直齒齒圈與斜齒齒圈。

在連續分度展成磨齒過程中，如果立柱不動，工作臺(及工件)與立柱(及砂輪)之間會產生很高的相對轉速(遠高于滾齒機或其他類型磨齒機的工作臺與立柱間的相對轉速)，超大的慣性力導致機床難以設計和實現。為減小工作臺(及工件)產生的慣性力，在相對轉速不變的前提下，讓立柱部件與工作臺部件同時反向旋轉，且兩者的回轉軸線同軸，可大幅度降低工作臺轉速。相對旋轉示意圖為圖2b。

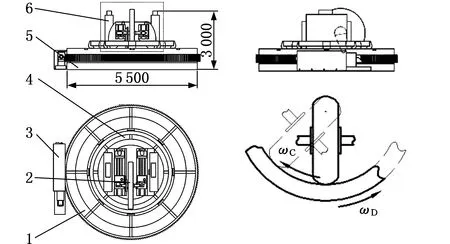
(a)球形蝸桿砂輪磨齒機結構(b)相對旋轉示意 1.組合工作臺部件 2.砂輪架部件 3.工作臺驅動系統 4.砂輪架進給系統 5.機床底盤部件 6.回轉型立柱部件圖2 球形蝸桿砂輪磨齒機結構布局Fig.2 Structure layout of gear grinding machine

選取回轉型立柱部件中的主立柱(不含可旋轉底座等)為研究對象，通過SolidWorks建立主立柱構件的幾何模型和主立柱的完整結構，見圖3，建模過程中忽略倒角、凸臺等一些細小結構。

圖3 主立柱結構Fig.3 The main column structure

2 原型立柱的有限元分析

主立柱的靜剛度和動態特性對磨齒機的加工精度有很大的影響，因此，在立柱的設計初期，需通過有限元分析來了解立柱的靜動態特性。本文主要分析主柱的應力應變、敏感方向的變形和前4階固有頻率，找出原型立柱設計的薄弱環節，為拓撲優化設計提供明確的方向。材料選取HT200，其力學性能參數見表1。有限元分析的具體步驟這里不贅述，僅列出分析結果，靜力分析結果見表2，靜力分析結果分布云圖見圖4。

表1 材料力學性能參數Tab.1 Properties of materials

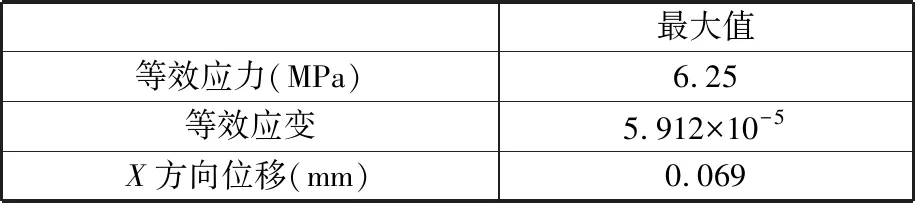
表2 靜力分析結果Tab.2 Static analysis results

(a)應力分布

(b) 應變分布

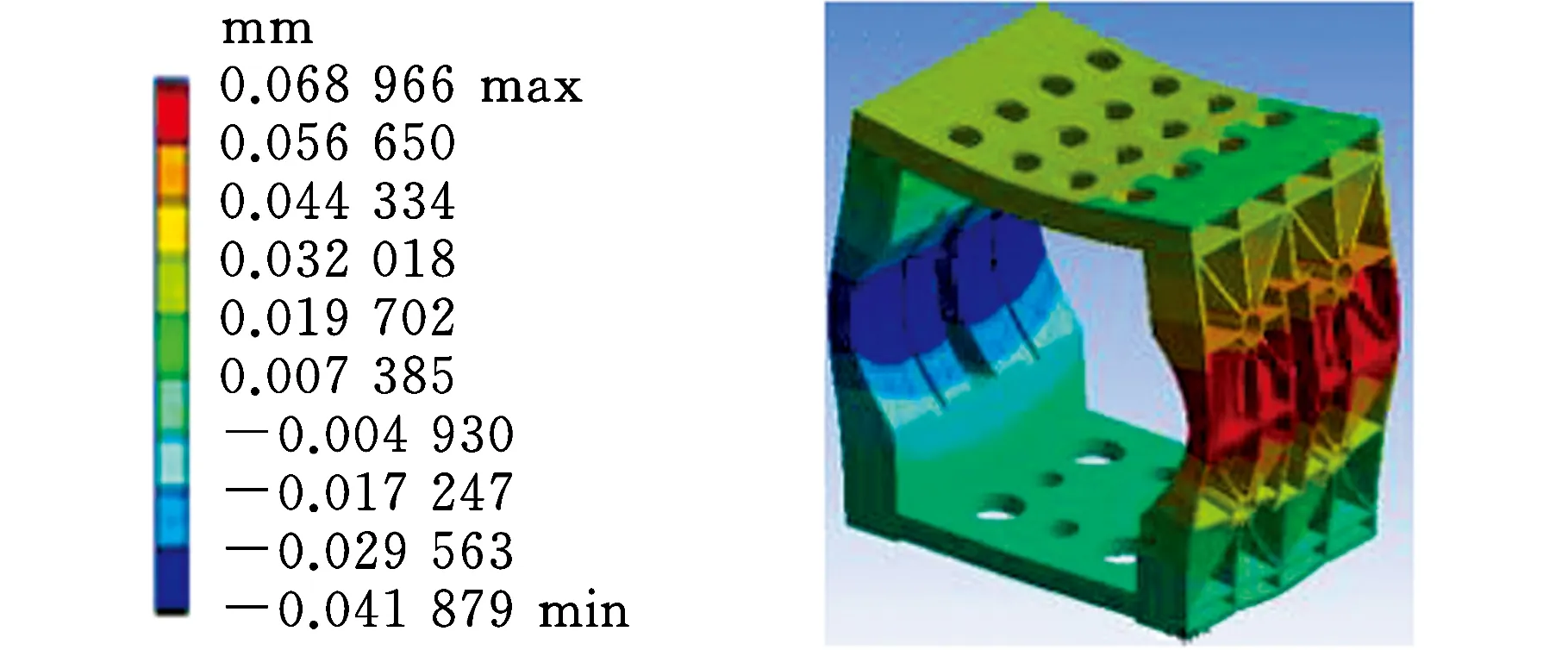
(c)X方向變形分布圖4 靜力分析云圖Fig.4 Static analysis cloud image

由于砂輪主軸的最高轉速為1 590 r/min，最大激振頻率為26.5 Hz，因而作用在立柱上的激振頻率不高，只有低階模態的固有頻率才有可能與激振頻率重合或接近，由此，本文提取前4階模態的固有頻率和振型進行分析，分析結果見表3。

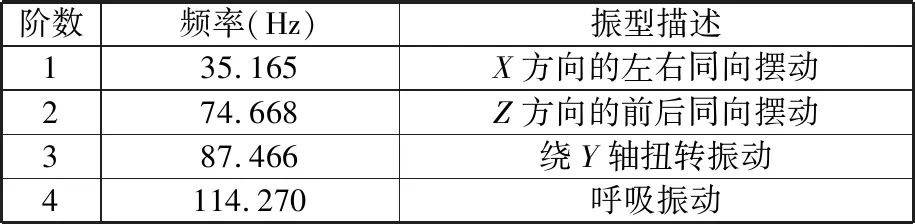
表3 模態分析結果Tab.3 Modal analysis results

前4階模態振型云圖見圖5。由模態分析的結果可以看出，立柱的1階固有頻率接近機床激振力的激振頻率，容易引起共振，因此，選1階固有頻率作為后續優化的一項參數。

(a)1階振型(頻率f1=35.165 Hz)

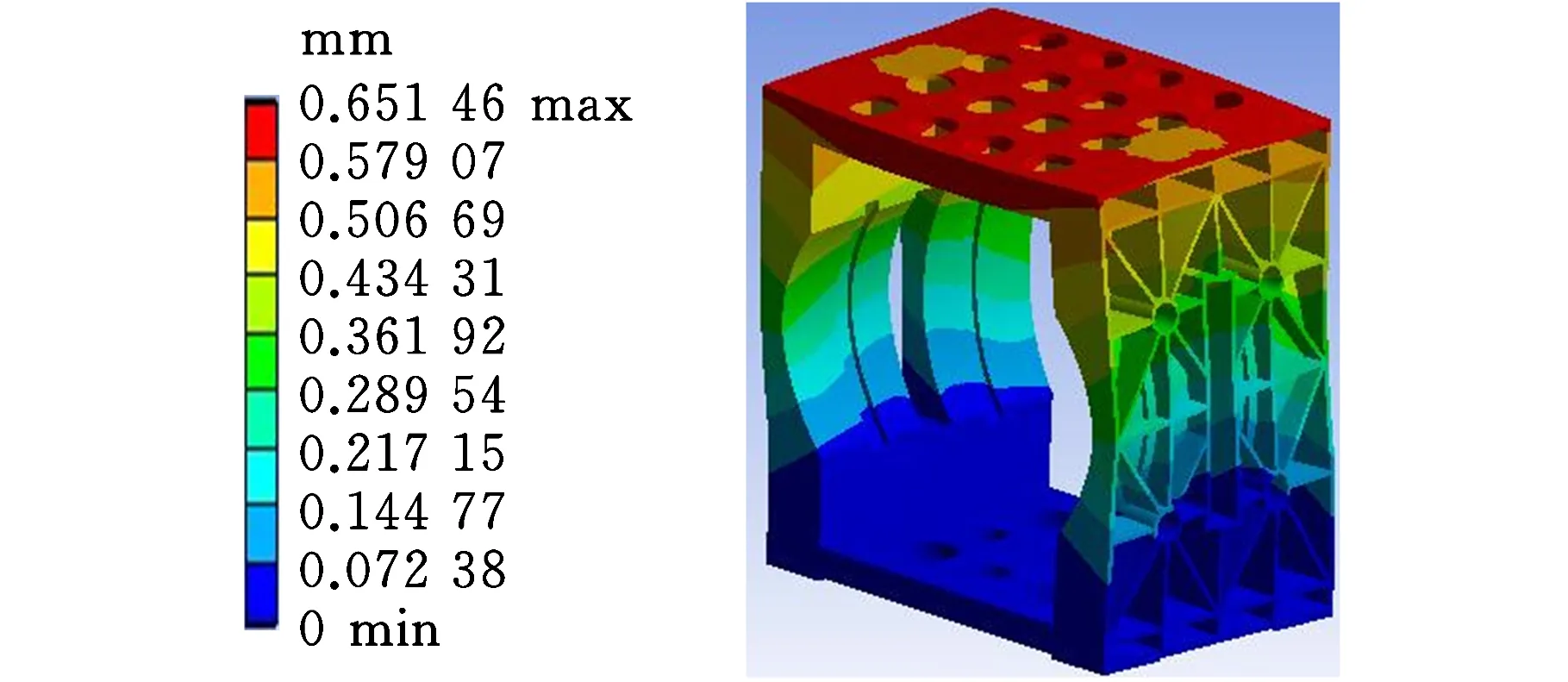
(b)2階振型(頻率f2=74.668 Hz)

(c)3階振型(頻率f3=87.466 Hz)

(d)4階振型(頻率f4=114.270 Hz)圖5 前4階模態云圖Fig.5 Vibration cloud images

3 立柱主體的拓撲優化

拓撲優化是在已知材料屬性和設計域內，通過優化設計方法得到滿足約束條件并使目標函數最優的結構布局形式及構件尺寸。通過有限元分析可知，立柱的靜剛度和1階固有頻率有待提高，可以分別以立柱的靜剛度、立柱的1階固有頻率為目標函數，進行各自的單目標優化；也可以同時考慮靜剛度與1階固有頻率進行多目標(這里即雙目標)優化。為了滿足輕量化的設計要求，以體積分數為約束，保證在不增大質量或質量略有減小的前提下，提高立柱的靜動態性能。根據目標函數的不同設置了3種優化方案。

(1)方案一。設計目標：應變能最小。設計約束：體積比設為0.3。設計變量：設計區域的偽密度。

(2)方案二。設計目標：1階固有頻率最大。設計約束：體積比設為0.3。設計變量：設計區域的偽密度。

(3)方案三。設計目標：加權應變能最小和加權模態最大化。設計約束：體積比設為0.3。設計變量：設計區域的偽密度。

通過Optistruct軟件，分別建立3個優化方案的數學模型，并對拓撲優化結果進行后處理，計算得到的拓撲優化結果見圖6。

4 立柱結構仿生優化

4.1 仿生優化

結構仿生是通過探究生物體的構造機理，利用“邏輯進化”與反求工程(RE)技術重構出“生物體結構”，通過結構相似來近似實現物理特性相似。

在結構仿生優化過程中，不僅要模仿生物體的整體物理結構及特性，更要探究其局部結構的構造特征與功能機理，以求為人類的設計提供 “優良構造”的典范。如蜂巢由排列有序的類六棱柱形子蜂房組成，子蜂房的底部由若干相同的菱形組成，構造出一種具有復雜變密度規律(對變密度規律和實現的研究目前仍屬熱點性難題)的輕量、堅固、以緊湊尺度形成大容量體的優異結構，這是人類用自研的優化手段難以實現的。人們仿其結構研發的蜂巢式結構具有強(剛)度高、質量小、隔熱、隔噪等特性，然而，蜂巢式結構難以制造。

仿生優化過程包括功能分析、相似性評價、邏輯進化設計和模擬實驗等。結構仿生優化設計的主體技術路線流程見圖7。

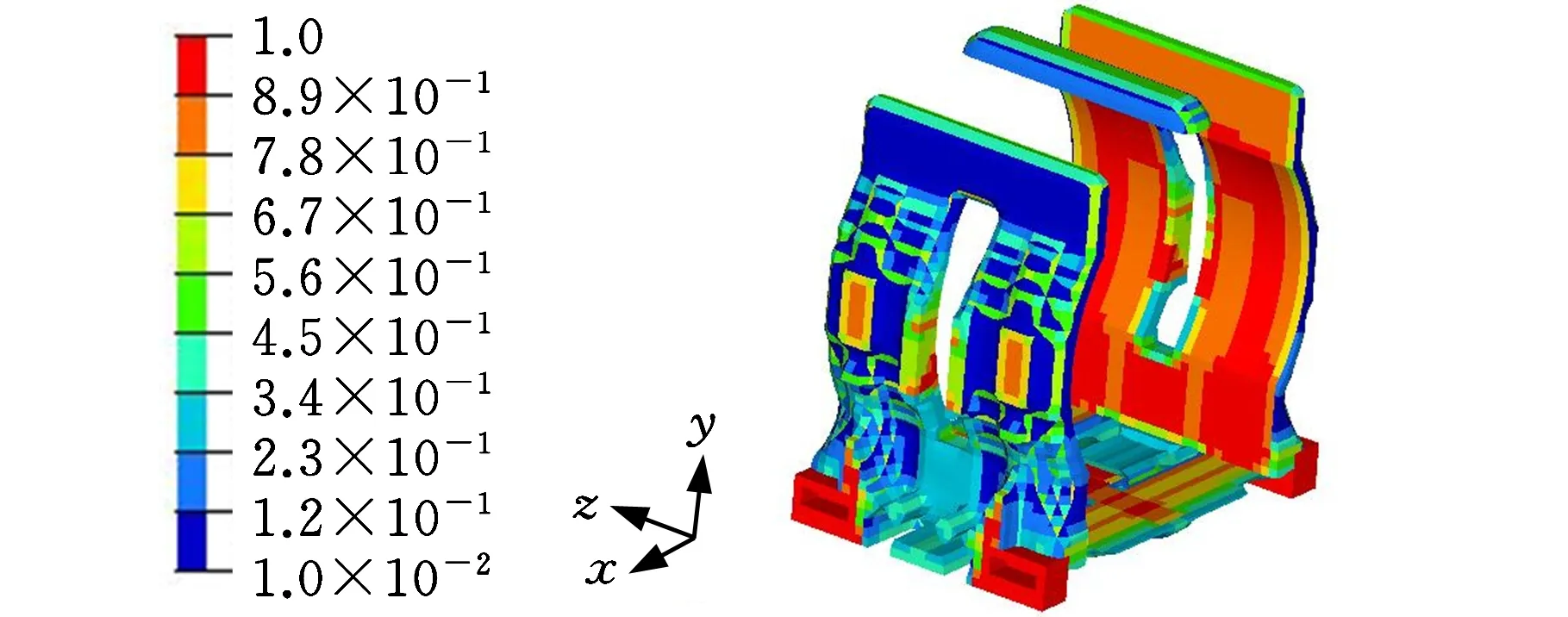
(a)方案一優化結果

(b)方案二優化結果

(c)方案三優化結果圖6 3種方案優化結果Fig.6 Optimization results

為驗證仿生優化的有效性，通常用RE技術重構其CAD模型，然后用有限元模擬分析結構性能。如果結果達到標準，則制作實體模型進行實驗驗證；否則，剖析出原因后重新選擇更合適的仿生結構。由此，結構仿生優化是不斷重復和改進直至獲得達標結果的過程。

4.2 仿生立柱的結構設計

根據立柱的高比剛度設計要求，選取王蓮和竹子為仿生對象。王蓮的葉脈結構和竹子的竹節結構都體現了完美的骨架結構，符合最佳的載荷傳遞路徑，能以最少的材料達到最大的負載能力[6]，且與立柱在結構、功能、載荷等方面都具有較高的相似性。由于拓撲優化能將結構的載荷路徑通過材料的分布體現出來，因此，結合上述拓撲優化的結果，借鑒王蓮葉脈和竹子竹節結構的構型原理，經過仿生邏輯進化，優化設計出立柱內部較復雜筋板的結構布局，如圖8所示。

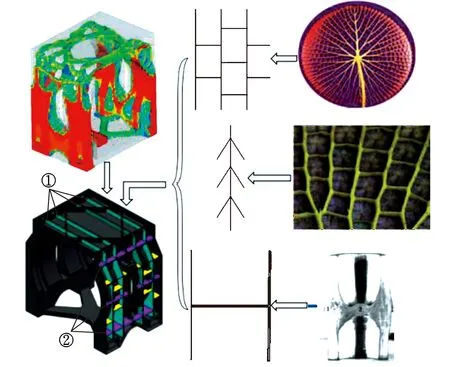
圖8 仿生立柱結構Fig.8 Bionic column structure

王蓮主葉脈起主要的支撐作用，所以在立柱載荷集中的左右弧形導軌處布置2個縱向隔板，并在2個隔板之間增加2個隔板，通過在側面布置4個縱向的隔板(圖中①部分)，保證立柱內外壁具有足夠的剛度，防止壁板出現局部的薄壁振動，同時便于內筋板的布置。根據竹節的結構特點，在立柱側壁布置橫向的隔板(圖中②部分)，使作用在導軌上的力可以通過橫向隔板傳遞到其他隔板上。根據王蓮相鄰葉脈的構型特點，通過在相鄰縱向隔板之間增加筋板(圖中淺色部分)，使導軌所受的力通過隔板和筋板傳遞到其他隔板以及外壁上，達到均化受力的效果。

5 立柱內部的尺寸優化

雖然經過拓撲優化與結構仿生優化可得到立柱結構的最佳布局，但是立柱內腔筋板的尺寸參數仍依據常規法設計。為獲得最佳拓撲結構下的最佳尺寸，對內腔筋板的參數進行尺寸優化。

通過靈敏度分析計算出各尺寸參數對立柱的結構性能參數(質量、敏感方向的變形(X方向)和1階固有頻率)的影響程度，有目的地選取對結構性能參數影響較為顯著的尺寸參數作為設計變量。立柱外形尺寸主要受安裝空間的限制，因此，只選取筋板厚度t1～t11和壁厚B共12個尺寸參數進行靈敏度分析，各參數的初始值按經驗法計算得出，各參數對應的立柱結構尺寸如圖9所示。

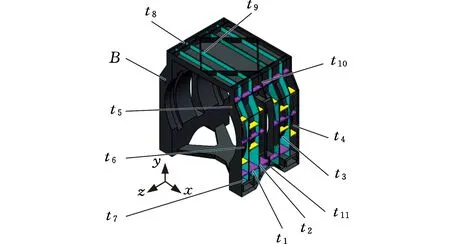
圖9 各尺寸參數Fig.9 Dimension parameters

經計算得到立柱質量靈敏度、總變形靈敏度和1階頻率靈敏度，如表4所示。綜合上述靈敏度分析結果，選取對質量、總變形和1階固有頻率影響都較大的壁厚尺寸B，縱橫筋板的厚度尺寸t1、t2、t3、t4、t6、t7以及局部筋板厚度尺寸t10、t11為優化變量。

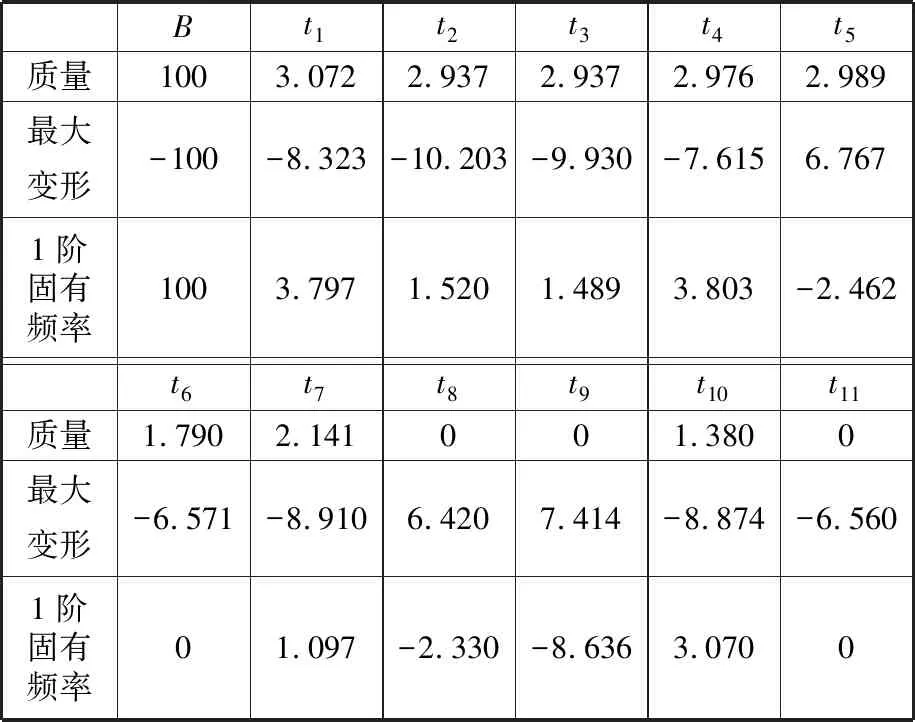
表4 立柱質量靈敏度、總變形靈敏度和1階頻率靈敏度Tab.4 The mass sensitivity, deformation sensitivity, first natural frequency sensitivity of column %

選取立柱質量m、靜剛度k和1階固有頻率f1為優化目標。其中質量越小越理想，靜剛度k和1階固有頻率f1則越大越好。優化模型為

V-minF(x)=f(min(m),min(-k),min(-f1))

式中，V為設計域(有質量)的體積；f(min(m),min(-k),min(-f1))表示對立柱的質量m求最小，對立柱的靜剛度k求最大，對立柱的1階固有頻率f1求最大。

經過優化計算后可以得到立柱優化前后的各尺寸參數變化，見表5。

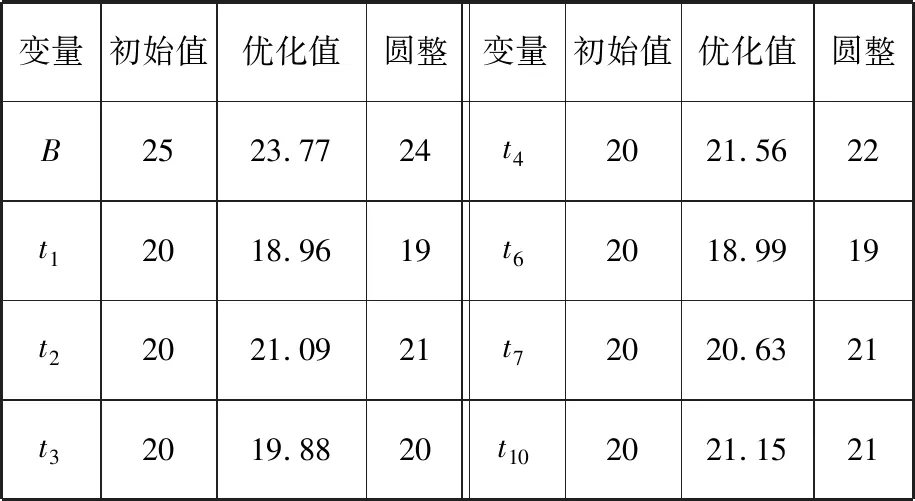
表5 設計變量參數Tab.5 Design variablesmm mm

將經過優化得到的數值插入到設計點列表并將其設置為當前設計點，更新生成新型立柱的參數化模型，對優化模型重新進行靜動態分析，對比優化前后立柱的性能參數(表6)，結果顯示，經拓撲優化、結構仿生優化、尺寸優化3種方法的綜合優化，在立柱靜剛度和1階固有頻率分別提高53.4%和5.46%的情況下，立柱質量減小了8.9%，證明了這種綜合優化方法在改進立柱靜動性能和輕量化設計上的有效性。

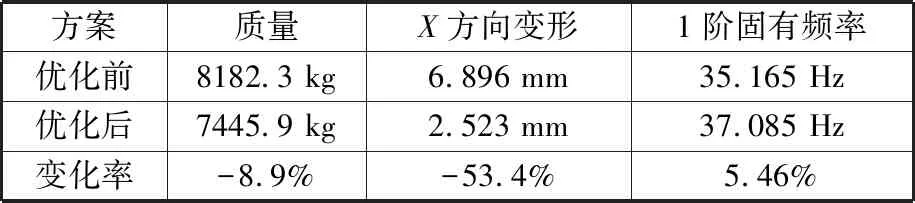
表6 優化前后立柱性能參數Tab.6 Column performance parameters before and after optimization

6 結論

以重型球形蝸桿砂輪磨齒機立柱為研究對象，研究了拓撲優化、結構仿生優化、尺寸優化3種方法在重(大)型機床復雜部件上的綜合應用。對比優化前后的結果可知，經過綜合優化的重型復雜立柱的靜動態特性都顯著改善。經綜合優化產生的新型立柱，在其體積、尺寸比例等與原型立柱基本相同的前提下，新型立柱的整體剛度與局部剛度均顯著提高。在載荷相同條件下，新型立柱(加工)敏感方向的變形量減小53.4%、質量減小8.9%、1階固有頻率提高5.46%。