考慮應(yīng)變率和溫度響應(yīng)的少煙NEPE推進劑粘彈性本構(gòu)模型

申依林，任 震，李軍強，馬 松

(1. 空軍駐西北地區(qū)軍事代表室，西安 710065；2. 解放軍95960部隊，西安 710089；3. 西安近代化學(xué)研究所，西安 710065)

0 引言

少煙NEPE推進劑是一類具備低特征信號和高能量水平的固體推進劑，在精確制導(dǎo)戰(zhàn)術(shù)武器中有著良好的應(yīng)用前景[1-2]。國內(nèi)對少煙NEPE推進劑的研制稍晚于NEPE推進劑，目前已在提高力學(xué)性能、拓寬燃速范圍、降低羽煙微波衰減等關(guān)鍵技術(shù)上取得一定進展。作為火箭發(fā)動機的部件，少煙NEPE推進劑在生產(chǎn)、裝配、儲存過程中會受到自身重量等低應(yīng)變載荷作用，且在運輸、點火和起飛、高過載轉(zhuǎn)彎等情況下又會受到高應(yīng)變率載荷作用；此外，因為導(dǎo)彈武器使用的氣候和地域不定，推進劑還要承受溫度載荷。所以，少煙NEPE推進劑的力學(xué)性能不僅與應(yīng)變有關(guān)，同時也受應(yīng)變率和溫度影響。而力學(xué)性能的優(yōu)劣直接關(guān)乎推進劑藥柱完整性及其它使用性能。因此，研究少煙NEPE推進劑在不同應(yīng)變率和溫度下的力學(xué)響應(yīng)，建立本構(gòu)模型，對于了解或分析火箭發(fā)動機在運輸、儲存過程中的受力情況具有重要意義。

固體推進劑的本構(gòu)模型常采用基于連續(xù)介質(zhì)力學(xué)的唯象學(xué)方法，如以應(yīng)變不變量為參數(shù)的超彈性多項式、Mooney-Rivlin模型[3-4]、Yeoh模型[5-7]及Ogden模型[8-9]等，還包括描述粘彈性質(zhì)的Maxwell模型[10]、Kelvin模型[11]、三參量固體模型[12]、Schapery模型[13]及ZWT模型[14]等。超彈性多以應(yīng)變能函數(shù)與偏應(yīng)變能和體積應(yīng)變能的標(biāo)量函數(shù)來反映，其中Mooney-Rivlin模型能較好地描述推進劑的單軸拉伸力學(xué)行為，但所得模量是常量，不適用于剪切和雙軸拉伸過程，且模型的準(zhǔn)確性與其階次呈正相關(guān)，準(zhǔn)確的模擬結(jié)果依賴高階次模型，同時使計算量增大；Yeoh模型對應(yīng)變能函數(shù)進行近似：忽略了Cauchy-Green張量的第二不變量I2對應(yīng)變能的影響，該模型形式簡便、常數(shù)項易獲得并可體現(xiàn)反“S”形應(yīng)力-應(yīng)變曲線的特點，但在處理復(fù)雜應(yīng)變狀態(tài)時偏差較大；Ogden模型是基于主伸長比的應(yīng)變能函數(shù)，其適用性較廣，高階模型可為大應(yīng)變過程提供近似解，但會造成累計誤差大、收斂困難等問題，因此高階Ogden模型的應(yīng)用受限。以上模型可反映推進劑應(yīng)力-應(yīng)變曲線的非線性特征，但在實際中推進劑變形時的應(yīng)力兼具應(yīng)變和率相關(guān)性，即具有粘彈特性，因此用粘彈性模型來描述更合適。在粘彈性模型中，以彈性和粘性元件形式組合成的Maxwell模型與Kelvin模型能直觀地解釋推進劑的粘彈性力學(xué)行為，但在階躍載荷作用下，Maxwell模型完全松弛無應(yīng)力，而Kelvin模型無瞬時響應(yīng)，這與實際情況不符；三參量模型是對Maxwell模型與Kelvin模型的改進，可反映推進劑的粘性松弛特性和瞬時彈性性質(zhì)，其適用性較好；Schapery模型從細觀損傷和不可逆力學(xué)的角度出發(fā)，提出偽應(yīng)變的概念，以偽應(yīng)變與損傷變量函數(shù)的乘積來反映材料的非線性粘彈特性，該方程形式靈活，能成功用于固體推進劑；ZWT模型是非線性彈簧和兩個Maxwell體的并聯(lián)形式，可考慮高、低應(yīng)變率對推進劑力學(xué)性能的影響，其結(jié)構(gòu)簡單、參數(shù)易獲取，但松弛時間是非線性回歸的結(jié)果，物理意義不明確。

本研究以少煙NEPE推進劑為例，在測試了應(yīng)變率和溫度對推進劑力學(xué)性能的影響后，建立了一種含多蠕變模式與非線性彈簧的本構(gòu)模型。該模型適用于寬的應(yīng)變率及溫度范圍，形式簡單且物理意義較明確，有助于理解少煙NEPE推進劑的粘彈特性，還可為固體火箭發(fā)動機的結(jié)構(gòu)設(shè)計及完整性分析提供支撐。

1 實驗

1.1 推進劑制備

各組分含量見表1。

表1 少煙NEPE推進劑配方

使用5 L立式混合機進行藥漿的混合，再澆注成方坯藥塊并在60 ℃固化7 d，按GB/T 528—1998標(biāo)準(zhǔn)制備啞鈴型拉伸樣條，如圖1所示。

圖1 啞鈴形推進劑試樣

1.2 性能測試

采用Instron 3300電子萬能材料試驗機進行單軸拉伸測試，其中拉伸速率分別為0.5、5、50、100、500 mm/min；測試溫度分別為50、20、0、-20、-40 ℃，在高溫或低溫測試前，對推進劑試樣保溫1 h。在每種條件下測試5次，除去非正常斷裂(從夾具處、圓弧處或缺陷處斷裂)的試樣，再求平均值得到推進劑在不同拉伸速率或溫度下的應(yīng)力-應(yīng)變曲線。

2 實驗結(jié)果分析

圖2 不同應(yīng)變率下的σ-ε曲線

圖3 不同應(yīng)變下的線性關(guān)系

從圖2中可見，隨著拉伸速率的增加，推進劑的斷裂強度σb、最大強度σm、斷裂延伸率εb和彈性模量(曲線初始斜率)均呈現(xiàn)增大的趨勢，說明少煙NEPE推進劑的力學(xué)性能存在著應(yīng)變率敏感特性。這是因為少煙NEPE推進劑交聯(lián)網(wǎng)絡(luò)的松弛速率較應(yīng)變速率相對滯后，導(dǎo)致在低拉伸速率下裂紋等缺陷可充分擴展，使推進劑試樣過早斷裂，而在高拉伸速率下則不然。進一步分析發(fā)現(xiàn)，定應(yīng)變條件下的應(yīng)力與對數(shù)應(yīng)變率呈線性關(guān)系，如圖3所示，且應(yīng)變越大，應(yīng)力對對數(shù)應(yīng)變率的變化越敏感。少煙NEPE推進劑應(yīng)力與對數(shù)應(yīng)變率的線性關(guān)系是下文研究力學(xué)性能率相關(guān)性的基礎(chǔ)。

本文還研究了溫度對少煙NEPE推進劑拉伸力學(xué)性能的影響。分別測試了拉伸速率為0.5～500 mm/min時，推進劑在-40、-20、0、20、50 ℃下的拉伸曲線，如圖4所示。從圖4可見，少煙NEPE推進劑的拉伸強度和初始模量均隨著溫度的下降而顯著增大。當(dāng)溫度下降后，高分子的鏈剛性增強、鏈間內(nèi)摩擦增大[15]，故其拉伸強度和模量大幅增加，但使用了PEG粘合劑的NEPE推進劑玻璃化溫度較高(-38 ℃左右)，因此低溫(-40 ℃)下延伸率較常溫下的略小。該實驗數(shù)據(jù)是下文中研究力學(xué)性能溫度相關(guān)性的基礎(chǔ)。

3 粘彈性模型的建立

為用模型反映少煙NEPE推進劑的線性對數(shù)應(yīng)變率效應(yīng)和溫度效應(yīng)，本文首先結(jié)合實驗分析了常用率相關(guān)模型的特征，對其改進并建立了適用于寬應(yīng)變率范圍的率相關(guān)模型；再根據(jù)力學(xué)性能的溫度變化特性，提出了溫度函數(shù)，結(jié)合前述模型最終建立起了粘彈性本構(gòu)模型。

3.1 率相關(guān)模型

為描述高分子復(fù)合材料的應(yīng)變率相關(guān)性，文獻[16-17]中提出了包含兩個Maxwell單元的非線性粘彈性模型。在該模型中，兩個Maxwell單元分別用于描述準(zhǔn)靜態(tài)和高應(yīng)變率下材料的力學(xué)性能，當(dāng)應(yīng)變率范圍不超過兩個數(shù)量級時，該模型的準(zhǔn)確性較好，具有借鑒意義；ZWT模型[14]包含兩個Maxwell單元和非線性彈簧，材料在高、低應(yīng)變率下的彈性和粘性響應(yīng)分別由Maxwell單元的模量Ei和松弛參數(shù)，θi來反映，該模型適合描述材料在準(zhǔn)靜態(tài)和高應(yīng)變率下的變形問題，其適用的應(yīng)變率范圍較固定，且Ei和θi是通過非線性回歸得到的參數(shù)，其物理意義不明確。若使用ZWT模型來擬合也可得到數(shù)學(xué)意義上的唯象參數(shù)，但不能直觀地反映線性對數(shù)應(yīng)變率效應(yīng)。

(a)500 mm/min (b)100 mm/min

(c)50 mm/min (d)5 mm/min

(e)0.5 mm/min

圖5 多蠕變模式與非線性彈簧并聯(lián)模型

圖5中的Ej和θj(j=1，2，…，n)分別為第j個Maxwell單元的彈性模量和松弛時間，Ee為非線性彈簧的彈性模量。

對于任一Maxwell單元，有

(1)

(2)

故本構(gòu)方程可表示為

(3)

σe=αε+βε2+γε3

(4)

使用實驗數(shù)據(jù)對式(3)進行回歸，可得到各蠕變模式的Ej和θj以確定推進劑的本構(gòu)方程，但直接得到各蠕變模式的松弛時間相差不大，其結(jié)果難以反映出多個蠕變模式的疊加效應(yīng)，因為擬合程序無法判別各個蠕變模式的差別，導(dǎo)致在使用包含兩個或多個蠕變模式的模型進行擬合時，其實際結(jié)果是同一種蠕變模式的多次累加。若能在擬合之前確定多個不同蠕變模式的松弛時間θj，則可通過非線性回歸得到各蠕變模式的彈性模量Ej，這樣一來，模型的物理意義更加明確。

(5)

圖6 ε和lgθ一定時，關(guān)系曲線

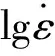
考慮將多個松弛時間不同的蠕變模式進行疊加，使各松弛過程“各司其職”：對于某一特定的松弛過程，當(dāng)對數(shù)應(yīng)變率變化較小時，其應(yīng)力與對數(shù)應(yīng)變率呈線性關(guān)系，而其它松弛過程在此范圍內(nèi)對材料的力學(xué)響應(yīng)為零或常數(shù)。這樣一來，該疊加的蠕變模式可在寬應(yīng)變率范圍內(nèi)描述材料的力學(xué)響應(yīng)。為此，將圖6中對數(shù)應(yīng)變率差值為2的曲線①、曲線②、曲線④和曲線⑧進行疊加，得到圖7中的曲線①；將圖6中對數(shù)應(yīng)變率差值為1的曲線③、曲線④、曲線⑥和曲線⑧進行疊加，得到圖7中的曲線②；圖6中對數(shù)應(yīng)變率差值為0.5的曲線⑤、曲線⑥、曲線⑦和曲線⑧進行疊加，得到圖7中的曲線③，如圖7所示。

圖7 多個蠕變模式的疊加

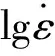
(6)

進而可得：

(7)

根據(jù)式(7)求得某一確定應(yīng)變下(為保證在高應(yīng)力區(qū)的擬合精度，本研究取0.4)，松弛時間與應(yīng)力-對數(shù)應(yīng)變率曲線上斜率最大點處(Pmax)應(yīng)變率的關(guān)系，見圖8。

圖8 lgθ與曲線上斜率最大點處的關(guān)系

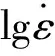
(8)

表2 對數(shù)應(yīng)變率和所對應(yīng)的松弛時間θ

由表2可見，與各對數(shù)應(yīng)變率對應(yīng)的松弛時間從0.61 s增至651.65 s，共跨越了4個數(shù)量級，考慮使用對數(shù)松弛時間為1的5個蠕變模式(θ分別為0.1、1、10、100、1000 s)進行疊加，以構(gòu)成少煙NEPE推進劑的粘彈性本構(gòu)模型，當(dāng)拉伸速率在0.5～500 mm/min之間變化時，可用5個蠕變模式的線性組合來反映推進劑的力學(xué)響應(yīng)。需說明的是，式(3)中使用多項式σe是為了表征推進劑的非線性彈性性質(zhì)，經(jīng)擬合后發(fā)現(xiàn)，三次多項式的效果較理想，σe的展開形式為αε+βε2+γε3。

將松弛時間以及各拉伸速率下的實測數(shù)據(jù)代入計算程序中進行多元非線性回歸，可得到模型中各參數(shù)的數(shù)值，其中非線性彈性部分的參數(shù)α、β和γ分別為1.971、-3.194和0.554；各蠕變模式的彈性模量及松弛時間見表3。

綜上可得少煙NEPE推進劑單軸拉伸的粘彈性本構(gòu)方程：

(9)

σe=1.971ε-3.194ε2+0.554ε3

(10)

3.2 溫度函數(shù)模型

在用模型反映推進劑力學(xué)性能的溫度相關(guān)性時，既有直接加入溫度項的方式[18]，也有采用率溫等效理論的方法[19]，而后者需應(yīng)變率與溫度能相互關(guān)聯(lián)，一般在模型上較難實現(xiàn)。本研究采用較直觀、有效地方法：在率相關(guān)模型的基礎(chǔ)上引入溫度函數(shù)項，來反映溫度對力學(xué)性能的影響，再根據(jù)不同溫度下的測試數(shù)據(jù)回歸出溫度函數(shù)中相關(guān)參數(shù)，最終建立起考慮應(yīng)變率和溫度響應(yīng)的本構(gòu)模型。

假設(shè)有溫度函數(shù)g(T)，加載過程的應(yīng)力為g(T)與率相關(guān)模型的乘積形式：

(11)

對于式(11)中的g(T)，分別使用過冪硬化函數(shù)和線性溫度函數(shù)，最終發(fā)現(xiàn)后者的擬合效果較好且又便于數(shù)據(jù)處理，因此本節(jié)使用線性函數(shù)來表示g(T)：

(12)

式中α為溫度因子，該參數(shù)可通過影響溫度函數(shù)從而決定應(yīng)力應(yīng)變曲線的形狀，α在給定應(yīng)變率下并非常數(shù)，而是T/T0的多項式形式。

值的說明的是，溫度函數(shù)g(T)中的參考溫度T0為20℃，其他溫度下的應(yīng)力值均是20℃的應(yīng)力應(yīng)變曲線與溫度函數(shù)的乘積。

將式(9)代入式(11)，可得少煙NEPE推進劑的率和溫度相關(guān)模型，再通過不同溫度下的實驗數(shù)據(jù)對該模型進行多元非線性回歸，得到α的表達式：

(13)

溫度函數(shù)g(T)的展開式：

(14)

歸并式(9)和式(14)，最終得到少煙NEPE推進劑本構(gòu)模型的展開式：

(15)

4 模型的實驗驗證

為驗證少煙NEPE推進劑粘彈性模型的準(zhǔn)確性，使用式(15)分別對不同拉伸速率和溫度下推進劑的應(yīng)力-應(yīng)變曲線進行預(yù)測，與實驗結(jié)果做了對比，如圖9所示，其中(a)～(e)是實驗和模擬曲線的比較，(f)和(g)是擬合結(jié)果偏離實測數(shù)據(jù)的百分誤差，百分誤差E%=|(ν-νfit)/ν|×100%，其中ν為實驗數(shù)據(jù)，νfit為擬合數(shù)據(jù)，E%反映了擬合值偏離實驗值的百分比率，以此反映該模型擬合效果的好壞。

(a)σ-ε,0.5 mm/min (b)σ-ε,5 mm/min

(c)σ-ε,50 mm/min (d)σ-ε,100 mm/min

(e)σ-ε,500 mm/min

(f)百分誤差,0.5、5、50 mm/min (g)百分誤差,100、500 mm/min

從圖9可見，實測和預(yù)測曲線符合地較好：在應(yīng)變?yōu)?.1～1.0的范圍內(nèi)，擬合百分誤差小于24%，而當(dāng)應(yīng)變小于0.1時，擬合誤差較大。這可能是由于為保證初始時刻的應(yīng)力為0，在實驗的初始時刻，推進劑試樣在夾具內(nèi)未完全固定至產(chǎn)生張力，在載荷作用下，試樣與夾具產(chǎn)生一定的滑移，而此時的測試值ν較小，導(dǎo)致百分誤差偏大。

總體而言，在較大的應(yīng)變范圍內(nèi)，模型的擬合效果較理想，說明多蠕變模式與非線性彈簧的并聯(lián)模型，以及率相關(guān)模型與溫度函數(shù)的乘積形式較適合描述少煙NEPE推進劑力學(xué)性能的應(yīng)變率與溫度相關(guān)性。該模型有助于更好地理解推進劑的力學(xué)行為，還可為本構(gòu)模型的發(fā)展提供思路。

5 結(jié)論

該模型結(jié)構(gòu)簡單，易于理解，且在寬應(yīng)變、應(yīng)變率及溫度范圍內(nèi)預(yù)測的準(zhǔn)確性較好。