基于Abaqus的干氣密封摩擦振動瞬時動態分析*

(蘭州理工大學石油化工學院 甘肅蘭州 730050)

在干氣密封環的開啟和閉合階段，由于槽所產生的動壓不足，兩密封面不可避免地產生干摩擦[1]。在對動靜環進行摩擦試驗的過程中，開啟和停止及變載變速的情況下摩擦界面出現了劇烈的摩擦振動及噪聲。目前，對于摩擦振動噪聲的研究，涉及到諸多領域，如鐵路機車制動[2-3]、汽車NVH[4-6]、石油勘探[7]等，但對于密封行業方面的摩擦振動的研究，國內外卻少有報道[8]。除清華大學高志等人[9]的干氣密封聲發射研究報道外，幾乎未見相關文獻。

在摩擦振動噪聲問題的研究中，有限元方法得到了廣泛的應用。與試驗方法相比，有限元方法既經濟又高效，大大節省了研究經費與周期。該方法還可輕松將復雜的摩擦表面實體化，在設計和計算具有表面織構[10]或其他復雜表面的問題中有較大的優勢。在此，本文作者借鑒汽車及機車制動領域有限元應用的成熟經驗及研究成果，對干氣密封動靜環摩擦振動進行有限元仿真分析。

目前，對于摩擦振動噪聲的有限元分析方法主要有2種：復特征值分析法[4-5,11-12]和瞬時動態分析法[2-3,10]。相比于復特征值分析法，近年來瞬時動態分析法得到了學者們的廣泛應用，其包含各種非線性因素的影響，便于在分析中考慮各種狀態及個監測點的時頻信息。如有限元模型完善，瞬態分析法可得到與試驗方法相對誤差很小的結果[3]。王曉翠等[10]利用瞬態分析法設計并驗證了織構界面在摩擦狀態時對摩擦振動的影響。張立軍等[13]基于Abaqus建立盤-銷系統的瞬態動力學模型，預測了摩擦過程中制動盤及銷的運動狀態，并結合復模態和部件約束模態計算驗證了其有效性。陳光雄等[2]利用瞬態分析法解決了地鐵某路線的小半徑曲線鋼軌波磨問題。張明明等[14]利用復特征值法與模態分析法結合的方法，討論了制動盤系統在特定情況下摩擦振動尖叫的規律。

根據干氣密封動靜環摩擦副的特點，本文作者采用瞬態分析法來討論其啟停階段干摩擦狀態下振動及噪聲的相關規律，建立真實工況下的有限元模型，探討干氣密封摩擦振動規律。

1 雙端面干氣密封有限元模型

1.1 有限元模型

文中所研究的對象為雙端面干氣密封，其主要應用于介質為有毒有害、易燃易爆的氣體場合及不允許有污染的食品加工和藥物加工過程。

應用UG軟件建立簡化模型爆炸圖如圖1所示。其主要參數如表1所示。應用Hypermesh軟件對模型進行結構網格劃分，得到的網格模型如圖2所示。該模型共有115 344個C3D8R網格以及112 640個節點，其中軸套網格數量為9 136，單枚動環網格數量為32 176，單枚靜環為20 928。動環、靜環及軸套的材料及性能參數如表2所示。

圖1 雙端面干氣密封簡化模型爆炸圖

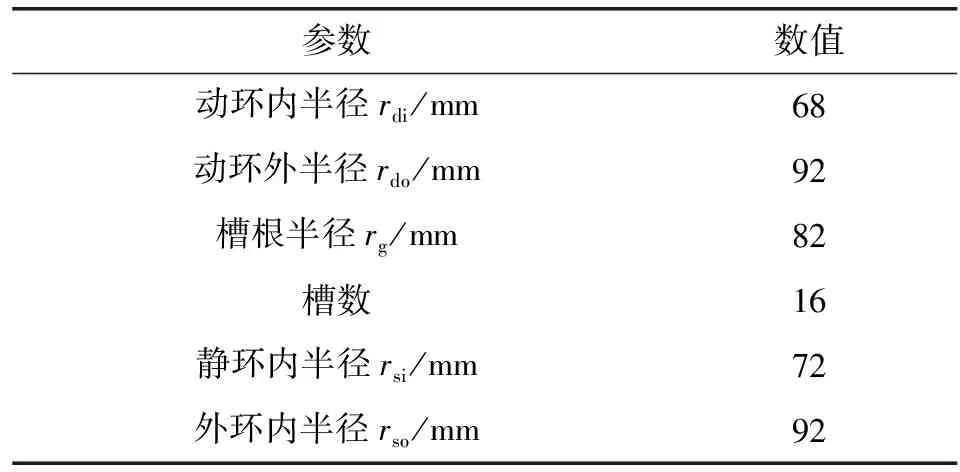
參數數值動環內半徑rdi/mm68動環外半徑rdo/mm92槽根半徑rg/mm82槽數16靜環內半徑rsi/mm72外環內半徑rso/mm92

圖2 干氣密封系統有限元模型

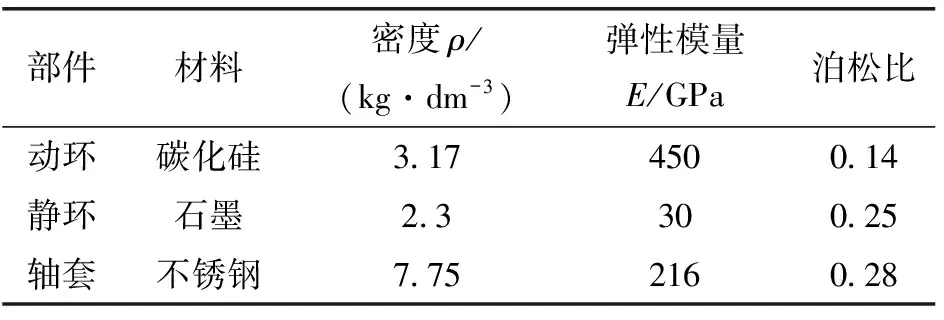
部件材料密度ρ/(kg·dm-3)彈性模量E/GPa泊松比動環碳化硅3.174500.14靜環石墨2.3300.25軸套 不銹鋼7.752160.28

1.2 瞬態分析

文中利用有限元分析軟件Abaqus/Explicit動力學顯示方法對模型進行分析，該方法應用中心差分法對運動方程進行顯式地時間積分，其動力學平衡方程[15]為

(1)

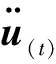
計算速度變化時設加速度為常數，利用前一個增量步中點的速度來計算當前增量步中點的速度值：

(2)

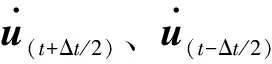
位移為

式中：u(t+Δt)為節點位移矢量。

根據采樣定理，采樣頻率ωs必須大于被分析信號成份中最高頻率ωmax值的兩倍以上：

即：

只有滿足此公式才能得到較為真實的信息。對于頻率較大的信號，Δt的取值要足夠小，但這也增加了Abaqus瞬態分析的時間。

1.3 基本假設

文中對該模型做如下基本假設：

(1)動環、靜環、軸套均為各向同性材料，材料的物理參數不隨時間的變化而變化；

(2)只考慮動環與靜環之間的摩擦，且摩擦過程中符合庫侖定律，既認為摩擦因數μ為常數，不隨摩擦過程而改變，且忽略O形圈對摩擦過程的影響；

(3)忽略裝置的結構阻尼、摩擦過程中的熱效應以及材料磨損對摩擦的影響；

(4)干氣密封在啟停階段由螺旋槽產生的動壓力較小，所以仿真試驗中忽略流體動壓力對開啟力的影響；

(5)由于文中忽略槽的動壓效應，為了避免跨尺度劃分網格，將動環螺旋槽槽深由微米級改為毫米級，此假設大大提高了計算效率，節省了計算時間。

定義干氣密封仿真試驗靜環受力分析如圖3所示，取合力并加載在靜環表面上。動環和軸套采用Tie連接，約束軸套除繞軸旋轉的其他5個自由度。定義密封壓力為1 MPa，彈簧力為50 N，環境壓力為標準大氣壓。摩擦因數設為0.2，施加速度約束為5 rad/s，檢測加速度的節點設置在靜環摩擦表面。

瞬態分析時間設定為0.06 s，按均勻間隔取6 000個時間節點數據。力與速度的加載歷程曲線如圖4所示。

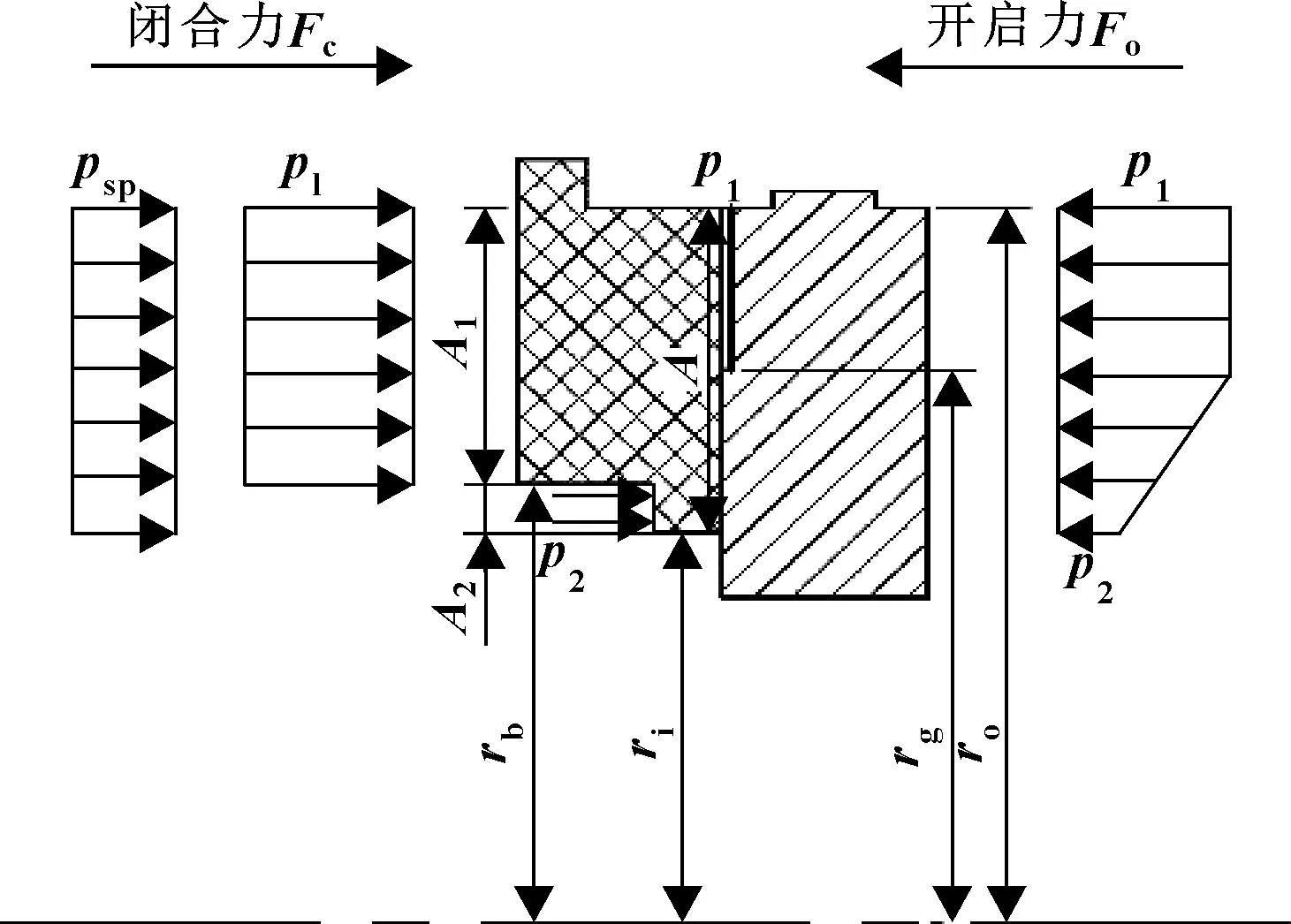
圖3 干氣密封仿真試驗壓力分布

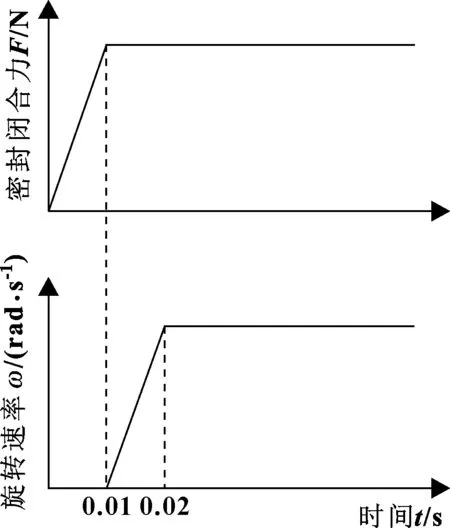
圖4 密封閉合力與速度加載歷程圖

2 結果與分析

2.1 槽及槽深對摩擦振動的影響

為了探究動環槽深對摩擦振動的影響，分別提取槽深為5、2、1 mm情況下靜環表面45314號節點時域信息，并對0.02 s后振動信號進行傅立葉變換，結果如圖5所示。可以看出，動環螺旋槽槽深對摩擦振動信息影響不大，因此可基于文中提出的基本假設(5)來提高動靜環摩擦過程的計算效率是可行的。

但無槽狀況下的接觸壓力與有槽時不同，由于無槽的情況下其密封開啟力隨環的半徑減小而單調遞減，又有其接觸面積的增加，所以在相同工況下兩密封環間會產生更小的開啟力。

無槽狀況下節點法向振動加速度時域信息如圖6所示，與圖6(a)相比可知，在相同密封壓力時無槽狀況相比有槽時振動更加劇烈。2種情況接觸壓力對比如圖7所示。

從圖7中可以看出，不管是無槽還是有槽情況下在前0.01 s內接觸壓力升高較為穩定,但在0.01～0.02 s加速階段，螺旋槽動環配對密封系統表現的接觸應力出現較大的不穩定波動。這是由于螺旋槽區域旋轉加速的能量積聚造成的，而無槽動環配對系統在該階段應力波動較為穩定。在經歷劇烈波動的加速階段之后，有槽密封系統所表現的接觸應力波動趨于穩定，波動幅度明顯小于無槽情況。

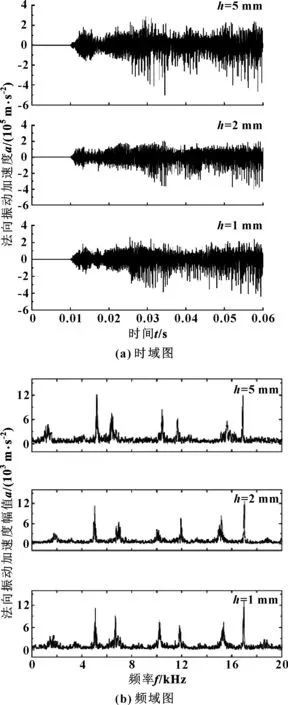
圖5 不同槽深時頻信息仿真試驗結果對比

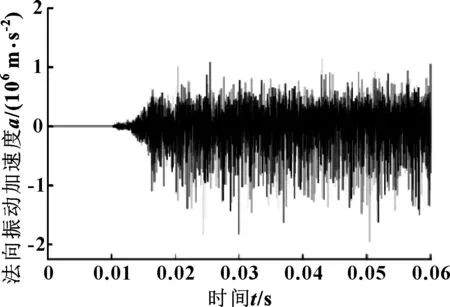
圖6 無槽情況下時頻信息仿真試驗結果

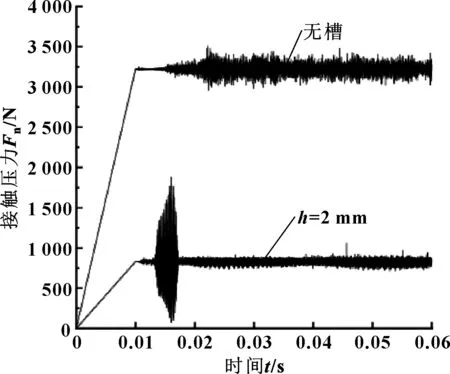
圖7 有無槽時頻接觸壓力結果對比

2.2 靜環材料及摩擦因數對摩擦振動的影響

近年來干氣密封動靜環材料的選擇及應用中出現了一種新型的“硬對硬”摩擦副設計，這種工程配對有效地降低了“軟對硬”(石墨-SiC配對)摩擦引起的應力變形[16]，但是也存在端面磨損嚴重等問題。文中采用SiC-SiC環模型對干氣密封“硬對硬”摩擦副進行分析。圖8所示為摩擦因數為0.2、槽深為2 mm時的時硬硬對摩時監測點的時域信息及表面接觸壓力歷程。

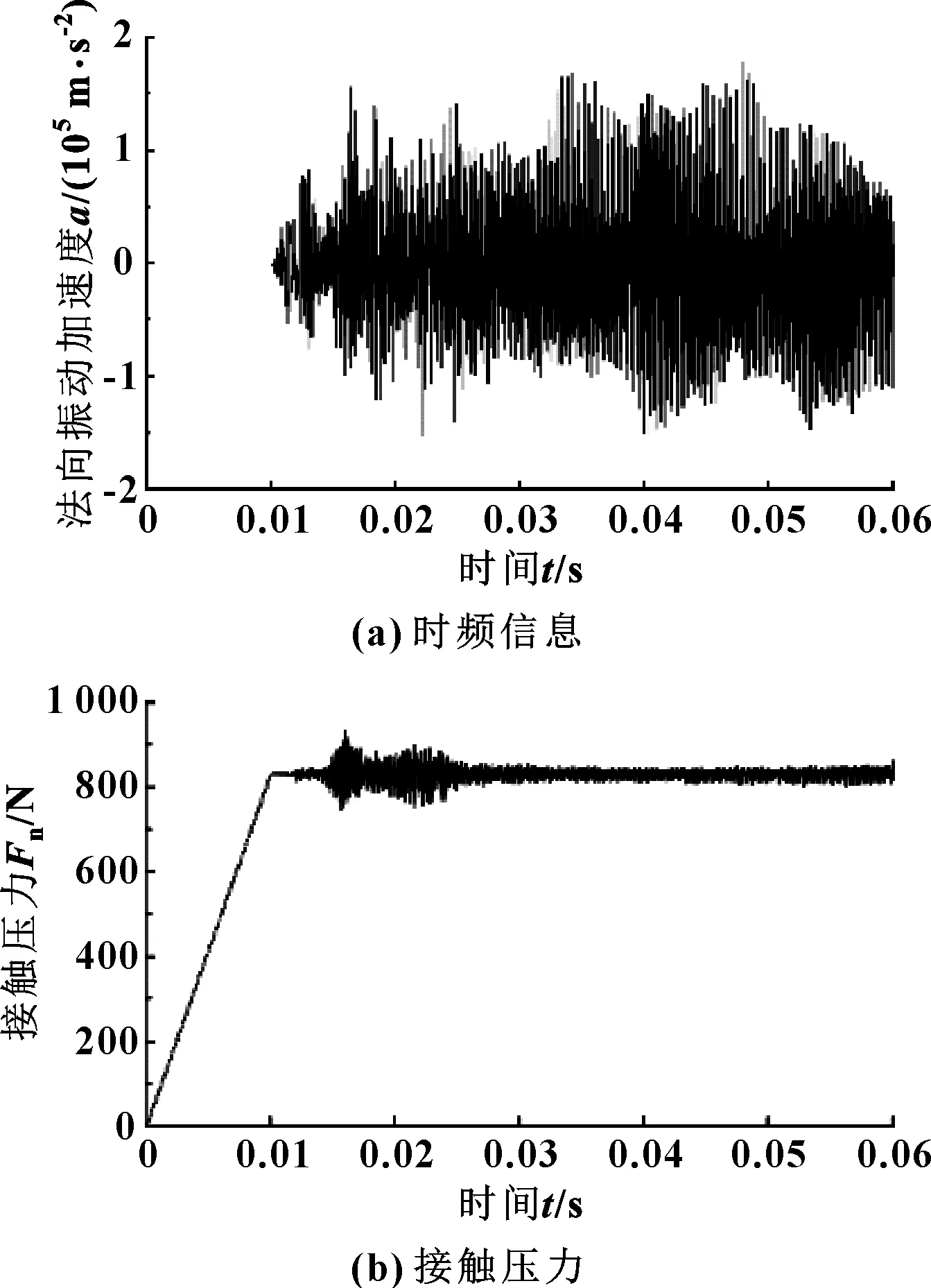
圖8 “硬對硬”接觸摩擦副振動加速度、接觸壓力時間歷程(μ=0.2)

對比圖8(a)及圖5(a)所示的槽深2 mm下的時域圖的可以看出，當摩擦因數相同時，“硬對硬”較“軟對硬”配合下的摩擦副振動幅度有小幅度降低，而比較圖8(b)和圖7可知，硬硬摩擦狀態下的接觸壓力在動環加速轉動時表現出更小的波動。可見，對于摩擦狀態下振動性能來說，雙SiC環配對要明顯優于SiC環與石墨配對。

為了提高端面的摩擦學性能，行業上對靜環表面采取鍍膜技術。具有表面薄膜的摩擦副滑動時，黏著點的剪切發生在膜內，其剪切強度較低。又由于表面膜很薄，實際接觸面積則由硬基體材料的受壓屈服極限來決定，實際接觸面積又不大，所以合理的鍍膜可以有效地降低摩擦因數[17]。假設薄膜對摩擦振動無影響，分別再對摩擦因數為0.1、0.08、0.06情況進行計算。為對比密封系統干摩擦狀態下不同摩擦因數下的平均振動幅度的大小，對0.02 s后的離散信號求解均方根值，如圖9所示。

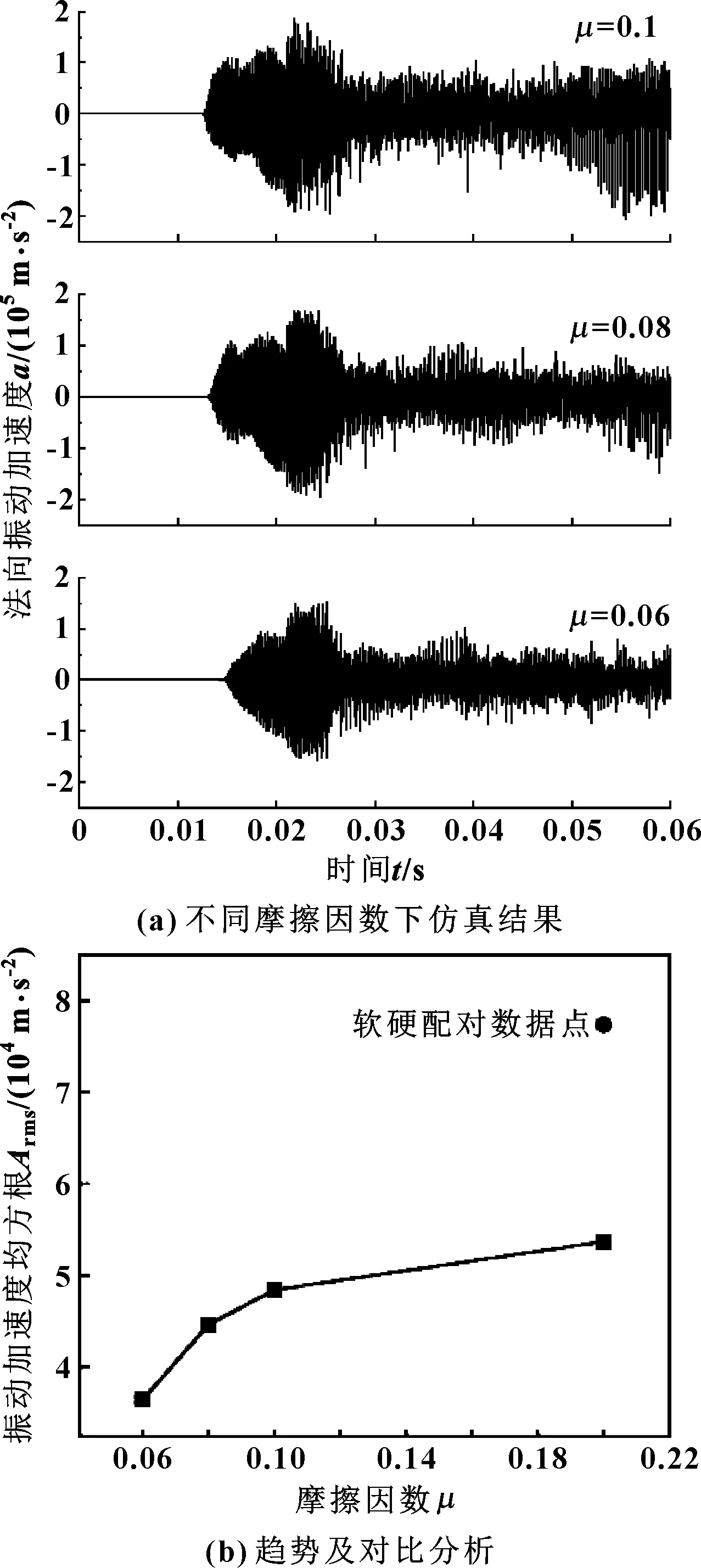
圖9 “硬對硬”情況下不同摩擦因數時仿真分析結果

當摩擦因數減小時，相應的摩擦振動幅度也會隨之降低。當摩擦因數由0.2降為0.1時，相應的振動加速度均方根有小幅度下降(降幅為0.1時，均方根減少大約為4%)；但當摩擦因數降為0.1以下時，振動均方根隨著摩擦因數的減少大幅度降低(在下降幅度僅0.02時，其均方根減少大于10%)，在圖9(b)中表現出的斜率更大。從圖9(a)中可以看出：摩擦因數為0.1時，“硬硬”配對在運行0.05 s后出現不穩定振動階段，隨著摩擦因數減小到0.08時，不穩定階段振幅降低；當摩擦因數等于0.06時，不穩定振動階段消失。由此可知，盡可能低的摩擦因數對降低摩擦振動波動幅值有很大作用。

圖5(a)中槽深2 mm下的摩擦時域信號的均方根值的計算結果為7.73×104m/s2,較相同狀態下雙SiC摩擦系統均方根值大44%左右。膜的作用間接地提高了密封環的防振性能，但“硬硬”配對在加速階段表現出的高量級振動也不容忽視。這可能是導致干氣密封鍍膜脫落的主要原因，也是今后探索研究的重點。

2.3 不同槽形對摩擦振動的影響

T型槽(T-DGS)干氣密封由于其端面槽型對稱，能適應雙向旋轉，而被廣泛地應用于石化、化工等行業用高速旋轉設備上。在相同工況下，對相同槽數、動壓槽根半徑、摩擦接觸面積的T型槽進行分析，其均方根對比如表3所示。可以看出，在相同摩擦因數、接觸面積相近的情況下，T型槽動環摩擦系統相對經典螺旋槽(S-DGS)來說，靜環監測點的法向加速度振動均方根要小大約20%，T型槽相對經典螺旋槽來說，具有較優越的摩擦振動性能。仿真結果可為今后試驗及工程應用提供參考。

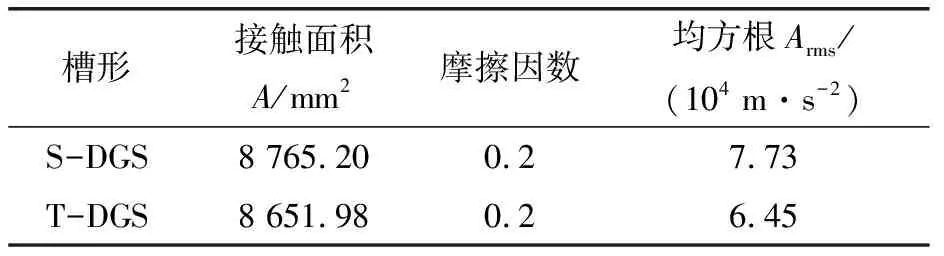
表3 槽形參數及RMS對比

3 結論

(1)通過對比槽深為5、2、1 mm情況下靜環表面監測節點時頻信息可發現，干氣密封動環槽深對摩擦振動的影響不大，依此假設建立的仿真研究具有可靠性。在同一密封壓力下，動環帶有槽的摩擦副振動幅度要明顯大于無槽情況。

(2) 雙SiC“硬對硬”密封環配對要明顯優于SiC與石墨“軟硬”配對，但在轉速增加時會出現振幅大幅度波動現象，這將是今后研究的重點。摩擦因數對密封環摩擦振動也具有較大影響，通過對雙SiC環不同摩擦因數的計算發現，當摩擦因數減小時，系統產生的不穩定振動會有明顯的降低。

(3) 在工況相同且動壓槽根半徑、摩擦接觸面積相近時，帶有T型槽動環的摩擦副較經典螺旋槽摩擦副表現出更好的摩擦性能。