基于預(yù)測函數(shù)控制的水面無人船航向控制器設(shè)計

夏云鵬 楊田田

（1.中船重工第七一三研究所 鄭州 450000）（2.武漢理工大學(xué) 武漢 430070）

1 引言

水面無人船是構(gòu)建海洋智能體系的重要組成部分。隨著無人船智能控制技術(shù)的發(fā)展，無人船在海事領(lǐng)域中的應(yīng)用也越來越廣泛［1］。無人船在推進(jìn)海事智能管理、提高海洋搜救應(yīng)急成功率等方面都有重要的應(yīng)用價值。

模型預(yù)測控制（MPC）算法因其先預(yù)測后控制的思想，使得其對于被控對象的控制響應(yīng)更加敏感，能夠更快地針對外部擾動變化調(diào)整控制動作；同時控制動作產(chǎn)生于其內(nèi)部優(yōu)化控制器的在線優(yōu)化過程，進(jìn)一步提高了控制系統(tǒng)對被控對象存在的不確定性的處理能力［2～4］。預(yù)測函數(shù)控制被稱為第3代MPC，其保留了MPC的基本特征，并加入對控制輸入進(jìn)行結(jié)構(gòu)化的步驟，將控制量分解為基函數(shù)的線性組合，提高控制輸入的規(guī)律性，降低算法參數(shù)在線計算量。依據(jù)MPC的上述特點，模型預(yù)測控制算法在無人船航向控制領(lǐng)域極具應(yīng)用價值。水面無人船本身存在操舵約束，其航行過程中還存在風(fēng)浪流等擾動，針對上述問題，本章采用預(yù)測函數(shù)控制算法設(shè)計無人船航向控制器，實現(xiàn)對航向的有效控制，并為間接航跡控制算法的設(shè)計提供支撐［5］。

2 基于經(jīng)典PID算法的航向控制器

經(jīng)典PID控制算法設(shè)計結(jié)構(gòu)簡單，在工程上已獲得廣泛的應(yīng)用。圖1表示了基于經(jīng)典PID算法的無人船航向控制系統(tǒng)。無人船航向控制系統(tǒng)為典型的負(fù)反饋系統(tǒng)，其輸入信號為無人船的目標(biāo)航向角ψd，輸出信號為無人船的實際航向角ψ；PID航向控制器的輸入信號為無人船目標(biāo)航向角ψd與實際航向角之間的偏差，輸出信號為無人船的舵角控制量。

如圖1所示，基于經(jīng)典PID算法的無人船航向控制器包括比例、積分和微分三個環(huán)節(jié)。基于經(jīng)典PID算法的無人船航向控制器的輸出信號與輸入信號之間的關(guān)系，可用式（1）表示。

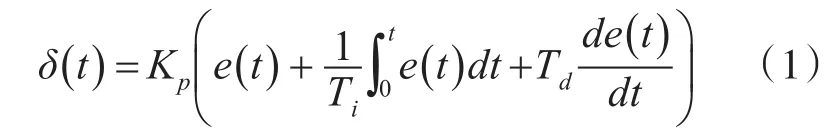
在進(jìn)行控制器設(shè)計時，為方便分析和整定參數(shù)，一般令 Ki=KpTi，Kd=Kp*Td，進(jìn)一步改寫式（2）為

其中，Kp為比例系數(shù)，Ki為積分系數(shù)，Kd為微分系數(shù)。

圖1 基于PID的無人船航向控制系統(tǒng)框圖

3 基于預(yù)測函數(shù)控制的航向控制器

基于預(yù)測函數(shù)控制（PFC）的水面無人船航向控制系統(tǒng)總體框圖如圖3所示。其中，航向控制系統(tǒng)的輸入信號為無人船的目標(biāo)航向角ψd，航向控制系統(tǒng)的輸出信號為無人船的實際航向角ψ，基于預(yù)測函數(shù)控制的航向控制器的輸入信號為無人船的目標(biāo)航向角ψd和無人船的實際航向角ψ，基于預(yù)測函數(shù)控制的航向控制器的輸出信號為無人船的輸入舵角控制量δ。水面無人船航向控制系統(tǒng)中的預(yù)測函數(shù)控制器的控制過程主要包括以下幾個步驟：

1）無人船預(yù)測模型根據(jù)當(dāng)前舵角控制量計算預(yù)測時域內(nèi)的無人船航向角預(yù)測輸出值。

2）根據(jù)無人船的當(dāng)前實際航向角輸出與預(yù)測輸出值的偏差對預(yù)測時域內(nèi)的預(yù)測輸出值進(jìn)行校正。

3）優(yōu)化控制器根據(jù)優(yōu)化性能指標(biāo)函數(shù)以及當(dāng)前無人船的目標(biāo)航向來計算控制時域內(nèi)無人船舵角控制量的最優(yōu)控制序列，并根據(jù)計算出的無人船舵角控制量的最優(yōu)控制序列確定當(dāng)前時刻施加于無人船上的舵角控制信號。

4）采用滾動優(yōu)化策略持續(xù)上述計算過程（如圖2），重復(fù)步驟1）～3）。

圖2 預(yù)測控制基本思想

根據(jù)以上控制過程，該航向控制器的設(shè)計主要涉及無人船預(yù)測模型的確定、優(yōu)化性能指標(biāo)的確定、反饋校正策略的制定以及預(yù)測時域和控制時域的參數(shù)選擇幾個方面。下面將從這幾個方面具體介紹基于預(yù)測函數(shù)控制的無人船航向控制器的設(shè)計過程。

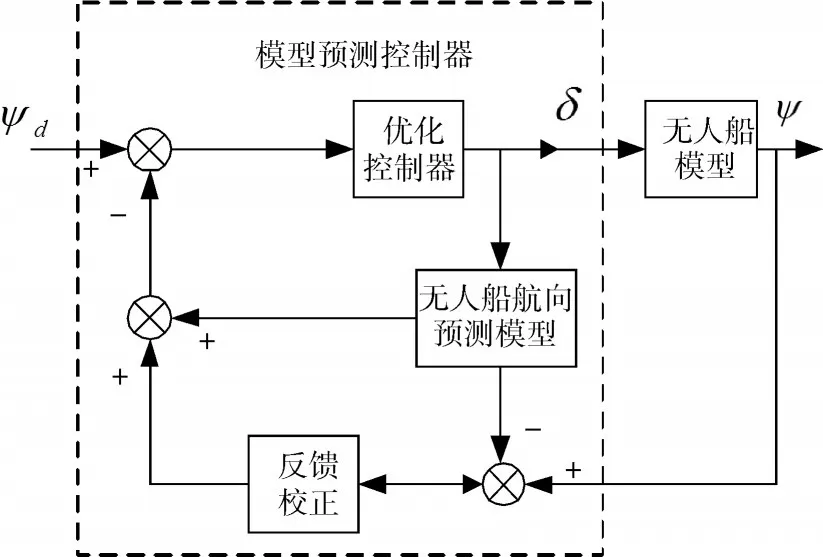
圖3 基于PFC的無人船航向控制系統(tǒng)框圖

3.1 預(yù)測模型

無人船航向控制系統(tǒng)的預(yù)測模型是指能夠正確描述航向控制系統(tǒng)輸入和輸出關(guān)系的模型。在進(jìn)行無人船航向控制研究時，采用能夠描述無人船操縱性特點的野本方程作為預(yù)測模型。野本方程表示為

其中，K表示無人船的旋回性指數(shù)，T表示無人船的追隨性指數(shù)。δ為無人船的舵角；ψ為無人船的艏向角。

取采樣時間為Ts，對方程式（3）進(jìn)行離散化，可得無人船預(yù)測模型的差分方程式表示為

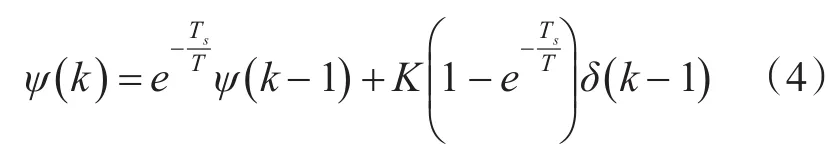
在方程式（3）中，無人船的旋回性指數(shù)K和無人船的追隨性指數(shù)T可以通過對已有實驗船進(jìn)行10°10°的Z形操縱性試驗來獲得。本文中的實驗船的基本參數(shù)如表1所示。

表1 無人船主要參數(shù)

在平靜的湖面進(jìn)行了實驗船的Z形（10°10°）試驗，獲得的實驗船艏向角和舵角關(guān)系變化曲線如圖4所示，根據(jù)文獻(xiàn)［6］中提到的計算方法，對無人船試驗數(shù)據(jù)進(jìn)行擬合，求得實驗船的K、T參數(shù)的值為K=0.49，T=1.94。

圖4 10°10°Z形操縱試驗結(jié)果

無人船在海上航行時容易受到風(fēng)、浪的干擾，將這些干擾 fa等效成舵角干擾添加到預(yù)測模型中，即將式（3）改寫為

3.2 反饋校正

基于預(yù)測函數(shù)控制（PFC）的無人船航向控制器中的反饋校正環(huán)節(jié)主要是對無人船預(yù)測模型給出的預(yù)測時域內(nèi)的航向預(yù)測輸出值進(jìn)行校正，以使其預(yù)測值更接近實際輸出值。此處采用k時刻已知無人船預(yù)測模型的預(yù)測輸出航向角ψm()k與系統(tǒng)實際輸出航向角ψ()k之間的誤差來校正系統(tǒng)未來預(yù)測時域內(nèi)的預(yù)測輸出航向角ψ^( )k+i。誤差表達(dá)式為

則校正后的系統(tǒng)未來預(yù)測時域內(nèi)的無人船預(yù)測模型的輸出航向角ψ^( )k+i表達(dá)式為

3.3滾動優(yōu)化

基于預(yù)測函數(shù)控制的航向控制器通過滾動優(yōu)化的方式來求解對應(yīng)于每一個時刻的最優(yōu)控制舵角輸入量，該舵角控制量的求取標(biāo)準(zhǔn)是控制器對于預(yù)設(shè)航向的跟蹤效果。另外，舵角控制量的選取在考慮航向最大化跟蹤的同時，要考慮舵角的變化量符合無人船操舵的實際情況［7］。因此，構(gòu)造如式（8）所示的標(biāo)準(zhǔn)函數(shù)J，對預(yù)測時域內(nèi)航向跟蹤誤差的平方以及控制時域內(nèi)舵角控制量變化增量的平方求加權(quán)平均值，并以標(biāo)準(zhǔn)函數(shù)J的最小化來獲得無人船最優(yōu)舵角輸入控制量。通過調(diào)整標(biāo)準(zhǔn)函數(shù)中的加權(quán)因子來反應(yīng)航向誤差以及舵角增量在求解控制時域內(nèi)最優(yōu)舵角控制量時的重要程度。通常情況下，在滿足無人船舵角約束的條件下，更注重航向控制效果，因此在式（8）中，航向誤差加權(quán)因子ai要設(shè)置的比舵角控制量誤差加權(quán)因子bi大。

其中，ψ是航向控制器的實際輸出航向角，ψr是無人船的參考航向角，Hp是預(yù)測函數(shù)控制的預(yù)測時域，Hc是預(yù)測函數(shù)控制的控制時域，且滿足Hc≤Hp，ai是航向誤差加權(quán)因子，bi是舵角控制增量加權(quán)因子。

另外，根據(jù)無人船本身的控制特點，模型預(yù)測航向控制器在輸出無人船的舵角控制量的過程中要考慮舵角約束。本文中使用的無人船模型舵角約束為

則滾動優(yōu)化中求取k時刻最優(yōu)舵角控制量問題可轉(zhuǎn)化為如式（10）表示的局部最優(yōu)控制問題，將k時刻式（10）求得的最優(yōu)控制序列的第一個控制值作為k時刻最優(yōu)舵角控制量作用于無人船航向控制系統(tǒng)，實現(xiàn)無人船的航向控制［8］。

4 仿真驗證及分析

本節(jié)以表1中介紹的無人船為基礎(chǔ)，在Matlab仿真環(huán)境中對所設(shè)計的航向控制系統(tǒng)進(jìn)行系統(tǒng)仿真，以驗證控制器的可行性。系統(tǒng)仿真主要涉及航向保持和航向跟蹤兩個方面。具體參數(shù)設(shè)置如下：

1）無人船初始參數(shù)設(shè)置為：航速v=1m/s，航向角ψ=0°。

2）PID航向控制器參數(shù)設(shè)置：Kp=0.5，Ki=0.00005，Kd=0.9 。

3）PFC航向控制器參數(shù)設(shè)置：預(yù)測時域Hp=10；控制時域Hc=2。目標(biāo)函數(shù)J中的航向誤差加權(quán)因子 ai=1，i=1，2，…Hp，舵角控制增量加權(quán)因子 bi=0.1，i=1，2，…Hc［9］。

4.1 航向保持效果

在無干擾的理想情況下，對兩種無人船航向控制器進(jìn)行航向保持效果仿真。給定目標(biāo)航向角ψd=10°的常值輸入，獲得的航向控制效果如圖5所示，舵角控制量變化情況如圖6所示。

圖5 航向保持效果圖（無干擾）

圖6 航向保持舵角控制量（無干擾）

由圖5和圖6的仿真結(jié)果可以看出，在無干擾的理想情況下，基于PFC的航向控制器和基于PID的航向控制器都可以無超調(diào)的達(dá)到給定的目標(biāo)航向角，基于PFC的航向控制器響應(yīng)速度比基于PID的航向控制器要快，但是其舵角控制變化量較大。

在進(jìn)行存在外部干擾的航向控制仿真中，風(fēng)浪干擾項用一個白噪聲乘以二階波浪函數(shù)來代替［10］，干擾信號中白噪聲信號的均值為2，功率譜密度為0.5；二階波浪函數(shù)表達(dá)式如式（11）所示，參數(shù)取值如下：增益常數(shù) Kω=0.42，主導(dǎo)海浪頻率ω0=0.606，阻尼系數(shù)ζ=0.3。

仿真實驗中的干擾信號如圖7所示。存在外部干擾情況下，兩種航向控制器的控制效果如圖8所示，對應(yīng)的舵角控制量變化情況如圖9所示。

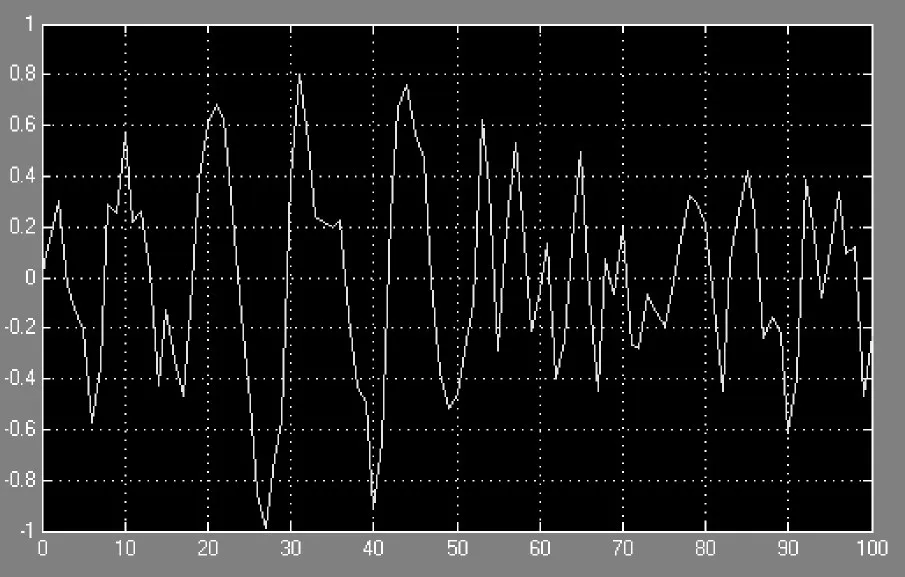
圖7 風(fēng)浪干擾信號

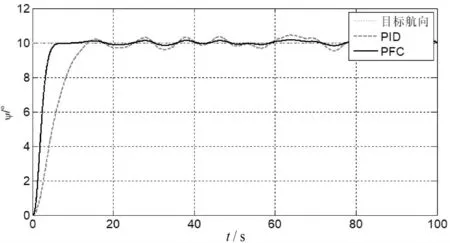
圖8 航向保持效果（存在干擾）

根據(jù)圖8和圖9所示的仿真結(jié)果可以看出，當(dāng)無人船航向控制系統(tǒng)存在外界風(fēng)浪干擾時，預(yù)測函數(shù)控制的控制效果要優(yōu)于經(jīng)典PID控制。由圖8的航向跟蹤曲線可以看出，基于預(yù)測函數(shù)控制的航向控制系統(tǒng)能夠更快地跟蹤到目標(biāo)航向，且在跟蹤目標(biāo)航向時的航向抖動更小［11～12］。由圖9的舵角控制量變化曲線可以看出，基于預(yù)測函數(shù)控制的航向控制器的輸出舵角控制量變化更加平滑。

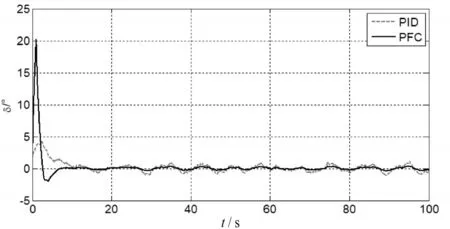
圖9 航向保持舵角控制量（存在干擾）

4.2 航向跟蹤效果

在無干擾的理想情況下，對兩種航向控制系統(tǒng)的航向跟蹤效果進(jìn)行仿真。航向跟蹤仿真實驗給定無人船的目標(biāo)航向角為幅值為90°、頻率為0.02rad/s的正弦信號。仿真實驗獲得的兩種控制器的航向跟蹤效果如圖10所示，舵角控制量變化曲線如圖11所示。

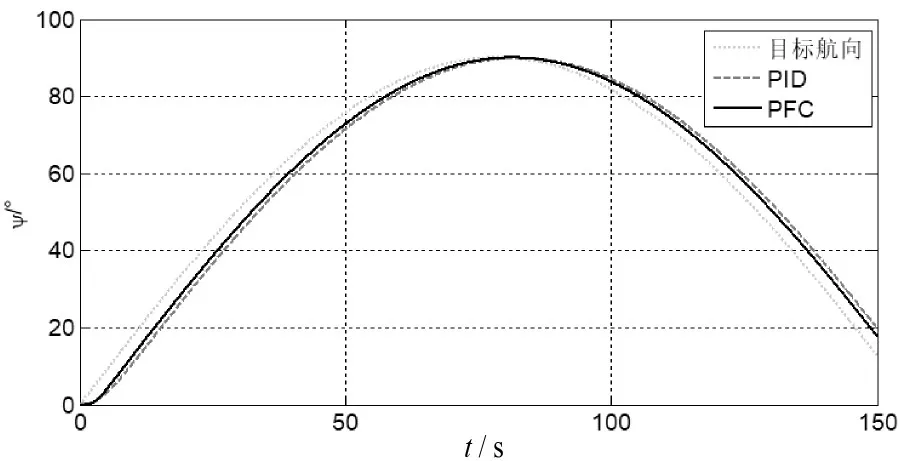
圖10 航向跟蹤效果（無干擾）

圖11 航向跟蹤舵角控制量（無干擾）

為了進(jìn)一步分析基于PID的航向控制器和基于PFC的航向控制器的控制效果，表2給出了兩種控制器的航向平均跟蹤誤差。從圖10、圖11以及表2可以看出，基于PFC的航向控制器能夠?qū)崿F(xiàn)穩(wěn)定的航向跟蹤性能，且跟蹤速度和跟蹤精度都高于傳統(tǒng)的PID航向控制器。

表2 航向跟蹤誤差

在存在外部干擾的情況下，給定無人船的目標(biāo)航向角輸入為幅值為90°，頻率為0.02rad/s的正弦信號，進(jìn)行兩種航向控制器的航向跟蹤效果仿真。干擾信號仍然采用式（11）所述的風(fēng)浪干擾，干擾信號如圖7所示。獲得的航向跟蹤效果如圖12所示，舵角控制量變化如圖13所示。

圖12 航向跟蹤效果（存在干擾）

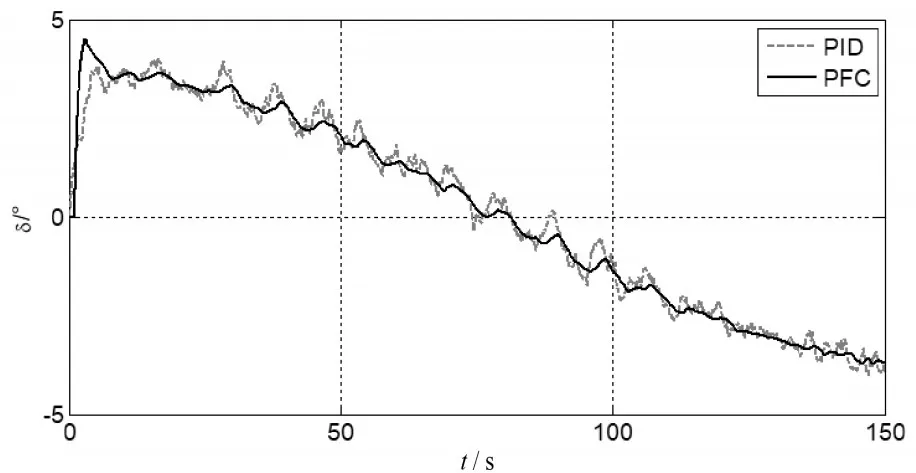
圖13 航向跟蹤舵角控制量（存在干擾）

為了進(jìn)一步分析基于PID的航向控制器和基于PFC的航向控制器的控制效果，表3給出了兩種控制器的航向跟蹤誤差。從圖12、圖13以及表3可以看出，基于PFC的航向控制器在有干擾的情況下也能夠?qū)崿F(xiàn)穩(wěn)定的航向跟蹤性能，且跟蹤速度和跟蹤精度都高于傳統(tǒng)的PID航向控制器。

表3 航向跟蹤誤差（有干擾）

5 結(jié)語

基于預(yù)測函數(shù)控制的算法原理，與無人船航向控制的要求相結(jié)合，提出了一種基于預(yù)測函數(shù)控制的水面無人船航向控制器。通過將該航向控制器與基于經(jīng)典PID算法的水面無人船航向控制器進(jìn)行航向保持和航向跟蹤的對比仿真實驗，驗證了基于預(yù)測函數(shù)控制的航向控制器有更好的航向保持和航向跟蹤效果。