灌漿凝結體強度參數(shù)的水—力耦合試驗研究及參數(shù)預測
楊昊天 王瑜鑫 王永翔
(中鐵西北科學研究院有限公司,甘肅 蘭州 730000)
1 概述
丹巴水電站工程壩址區(qū)覆蓋層具有厚度大、結構及組成復雜、力學性質差等特點,對壩基處理總體方案為上部20 m采用回填石渣料并固結灌漿,這一層稱為回填層,下覆50 m(主要地層為崩坡積層,③-1層,③-2層)采用高壓旋噴灌漿。壩基加固處理后,其壩基加固材料的力學性能及閘壩的穩(wěn)定安全性是工程關心的核心問題。特別是在大壩長期運行過程中,壩基承受水壓力作用下其強度參數(shù)的弱化程度值得研究,可對工程加固措施的評價和優(yōu)化提供重要參考。
對現(xiàn)場取得的灌漿凝結體試樣進行應力—靜水壓力耦合試驗,并通過地質—力學分析、數(shù)理統(tǒng)計分析的方法定量揭示了凝結體的強度特性,并對大壩運行工況下壩基加固的灌漿凝結體強度參數(shù)做出了預測。
2 試驗方案及試驗儀器
為了確定加固壩基在不同圍壓、不同水壓作用下的強度參數(shù),對現(xiàn)場采取的凝結體試樣進行了應力—水壓力耦合的三軸試驗,每個地層的試樣均進行4級水壓(0 MPa,0.4 MPa,0.8 MPa,1.2 MPa),及每級水壓對應進行7級圍壓(2 MPa,3 MPa,4 MPa,5 MPa,6 MPa,7 MPa,8 MPa)下的三軸試驗。
本次試驗采用的儀器是美國產(chǎn)MTS815 Flex Test GT巖石力學試驗系統(tǒng)。試驗機具有地殼應力場、地下水滲流場、地溫溫度場、地震動力場多場耦合試驗功能,可測得試樣的圍壓、軸向偏應力、孔隙水壓、試樣兩端頭的孔隙水壓差及軸向變形、環(huán)向變形等參數(shù)。
3 成果分析
3.1 強度參數(shù)的圍壓效應
為了揭示抗剪參數(shù)與應力條件的關系,在試驗數(shù)據(jù)整理過程中,計算c,f值時以每相鄰的4個圍壓進行,所以7個圍壓可以分為4個級別,如圍壓2 MPa~5 MPa為第Ⅰ級別,以此類推。圍壓的范圍分級如表1所示。
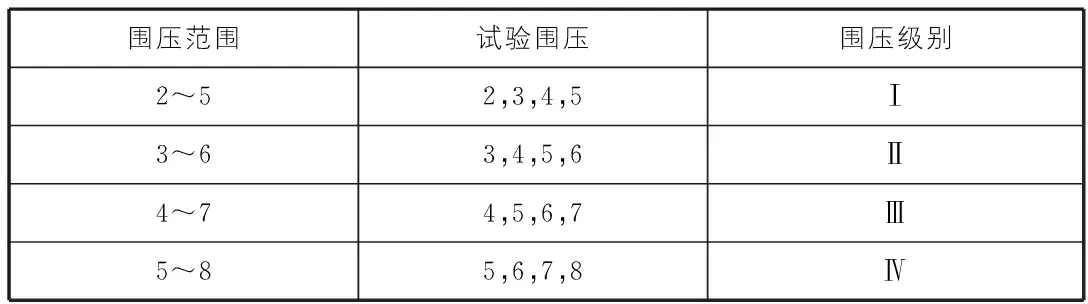
表1 圍壓范圍分級 MPa
針對以上四個圍壓級別,對抗剪參數(shù)c,f值分別進行整理分析,取典型水壓下(0.4 MPa)每個地層的圍壓級別與c,f值的關系曲線,分析其結果和規(guī)律。
3.1.1 凝聚力c的圍壓效應
通過統(tǒng)計回填層、崩坡積層、③-1層、③-2層在各水壓下的不同級別圍壓的凝聚力c值,考察凝聚力c與圍壓的關系,c值與圍壓的關系曲線如圖1所示。
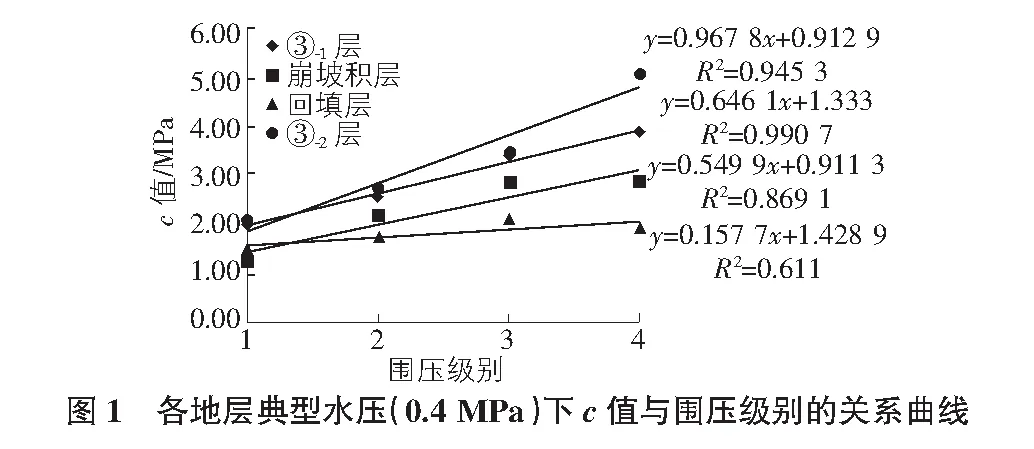
由各個地層在0.4 MPa水壓的計算結果可以看出,凝聚力c值有明顯的圍壓效應,線性擬合方程的斜率在15%~96%之間,即凝聚力c值在較低圍壓下計算結果小于在較高圍壓下的計算結果,這個現(xiàn)象從c值的物理意義來看可以解釋為,隨著試樣周圍圍壓的增大,使試樣被擠壓導致其內部物質分子之間的距離減小,從而使凝聚力增大。
3.1.2 摩擦系數(shù)f的圍壓效應
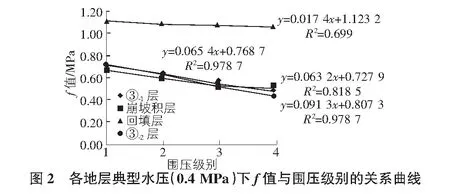
通過統(tǒng)計回填層、崩坡積層、③-1層、③-2層在各水壓下的不同級別圍壓的摩擦系數(shù)f的值,考察f與圍壓的關系,f與圍壓的關系曲線如圖2所示。
通過計算結果看出,f值與圍壓級別擬合線性關系的斜率較小,在-1%~-9%之間,說明雖然隨著圍壓級別的增大,f值表現(xiàn)為減小的趨勢,但f值的圍壓效應較不明顯。
對于以上討論強度的圍壓效應可以用非線性強度理論來解釋:莫爾圓的包絡線嚴格來說不是一條直線,而是一條曲線,該曲線的特點就是隨著應力水平的增大,包絡線的切線斜率逐漸減小,也就是說隨著應力水平的增大,包絡線切線在y軸的截距增大,而斜率減小,即c值增大,摩擦系數(shù)f減小。
3.2 強度參數(shù)的水壓效應
本次試驗在每級圍壓下設定了四級水壓:0 MPa(飽水狀態(tài))、0.4 MPa,0.8 MPa,1.2 MPa,試驗圍壓共有7級,在討論強度參數(shù)水壓效應時的c,f值是在7級圍壓下計算得到的,其結果和規(guī)律如下。
3.2.1 凝聚力c的水壓效應
各地層c—Pw的關系曲線如圖3所示。

從圖3可以看出,各個地層的凝聚力c值都因水壓的增大而減小,并且凝聚力c值與壓力均呈現(xiàn)出較好的線性關系,相關系數(shù)的平方都達到了90%以上。其中回填層的c值在水壓為1.2 MPa時為0 MPa。
3.2.2 摩擦系數(shù)f的水壓效應
各地層f—Pw的關系曲線如圖4所示。

從圖4可以看出,各個地層的摩擦系數(shù)f值隨水壓的變化規(guī)律并不一致,其中崩坡積層、③-1層和③-2層的f值隨著水壓的增大有減小的趨勢,但是減小的幅度很小,其擬合線性關系斜率在-2%~4%,線性趨勢線基本呈水平狀態(tài),回填層的f值隨著水壓的增大有升高的趨勢,但增大幅度不是很大。綜合來看f值的水壓效應不甚明顯,在工程應用中可以忽略不計。
3.3 強度參數(shù)預測模型
3.3.1 凝聚力c值的預測
通過以上分析看出,凝聚力c值有明顯的圍壓效應、水壓效應,通過系列水—力耦合試驗得到相應凝聚力c值,則可以在水庫運行工況下強度參數(shù)c提出以下預測模型。
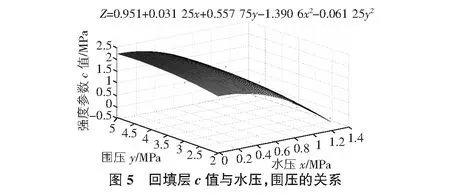
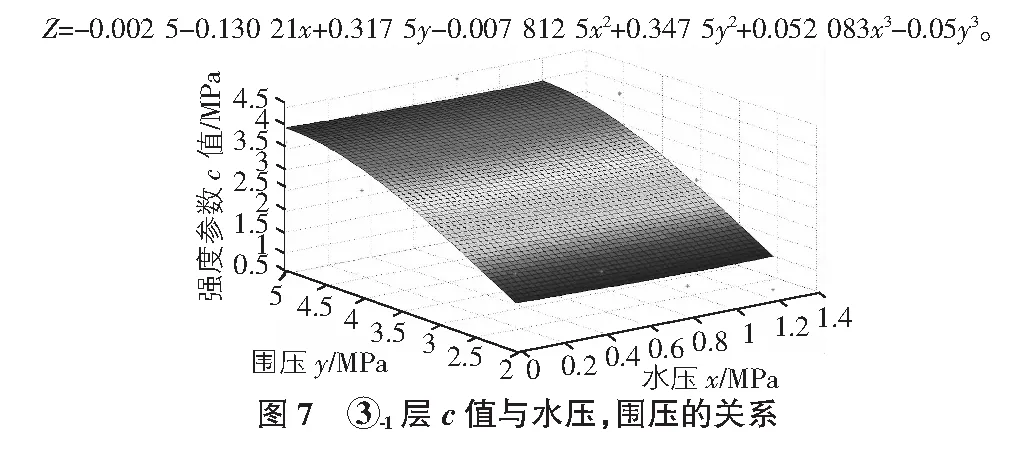
以水壓Pw為x軸,圍壓σ3為y軸,強度參數(shù)c為z軸,繪制了c—Pw—σ3的空間散點圖,并擬合一個空間曲面,擬合曲面精度較高,規(guī)律較好,滿足工程需要。各地層的c—Pw—σ3關系曲面圖如圖5~圖8所示。
從擬合的關系曲面中整理得到每個地層抗剪強度參數(shù)c值關于變量σ3,Pw的預測模型如表2所示。其中從R2(擬合方程的復相關系數(shù)的平方)的數(shù)值可以看出方程與試驗值擬合關系較好。


3.3.2 摩擦系數(shù)f值的預測
從上節(jié)的分析可以看出,各個地層的摩擦系數(shù)f值的圍壓效應、水壓效應均不甚明顯,所以認為在工程應用中摩擦系數(shù)f值的水壓效應和圍壓可以忽略不計。各地層f值的取值是由圍壓2 MPa~8 MPa的7級圍壓下計算得到,由于忽略水壓對f值的影響,所以可以把4級水壓力看成是4組平行試驗,即取4級水壓下f值的平均值作為工程建議值。各地層的f值如表3所示。

表2 強度參數(shù)c值預測模型 MPa

表3 強度參數(shù)f值預測模型
4 結語
回填層、崩坡積層、③-1層及③-2層灌漿凝結體的強度特性主要通過工程重點關注的抗剪強度參數(shù)c,f值表征,討論了各地層強度特性的圍壓效應和水壓效應,分析試驗結果主要得到以下幾點認識:
1)凝結體的強度特性有較為明顯的圍壓效應,其抗剪強度參數(shù)與試樣的應力條件有很大的關系:當試樣在較低圍壓級別下所計算得到的凝聚力c值較小,反之在較高圍壓級別下得到的凝聚力c值較大,摩擦系數(shù)f值受圍壓的影響不太明顯。
2)各地層的抗剪強度參數(shù)c具有明顯的水壓效應,其隨著水壓的增大而減小,并且有較好的線性關系;而水壓對抗剪強度參數(shù)f的影響很小,在工程應用中建議可以不考慮f值的水壓效應。
3)提出了試驗范圍內強度參數(shù)c值關于圍壓σ3和靜水壓力Pw兩個自變量的預測模型如表2所示,對參數(shù)f值的取值如表3所示;根據(jù)水—力耦合試驗所建立的預測模型,可計算得到各地層在其地應力、水壓力條件下的強度參數(shù)值,為工程設計提供參考。

