同步擠壓改進短時傅里葉變換分頻相干技術在斷裂識別中的應用
嚴海滔 周懷來 牛 聰 巫南克 周 健
(①成都理工大學地球物理學院,四川成都 610059;②油氣藏地質及開發工程國家重點實驗室,四川成都 610059;③中海油研究總院,北京 100028)
0 引言
斷裂的精確刻畫是地震資料解釋中的一大難題,1995年Bahorich等[1]提出了地震相干數據體的計算方法,使斷裂的自動解釋成為可能;地震相干技術自20世紀90年代中期Amoco公司成功地應用于地震資料斷裂解釋以來,取得了長足的進展。1998年Marfurt等[2]提出了基于相似性計算的第二代相干體算法,比第一代互相關算法具有更高的斷裂刻畫能力。1999年Gersztenkorn等[3]提出了基于本征結構的第三代相干算法,較第一、二代算法具有橫向分辨率高、抗噪性強的優點。諸多學者仍在不斷改進、發展新的相干算法,王西文等[4]結合時頻分析方法(小波變換)與相干算法,使分辨率比傳統相干算法更高。
1999年Partyka等[5]提出了譜分解方法,將全頻帶的地震數據體分解為不同頻率的數據體,以突出地震數據中一些不同尺度的地質體。2009年Zeng等[6]發現某些單頻地震數據體比常規的全頻帶數據體對地質體的邊界、范圍的刻畫更加清晰,細節更加豐富,為頻率域的斷裂解釋提供了新的思路。但是受時頻分析算法分辨率的影響,結果往往出現一些誤差,因此,只有利用高時頻分辨率算法在時頻域的斷裂刻畫,才能得到更為準確的結果。
2011年Daubechies等[7]在小波變換的基礎上提出了同步擠壓變換方法,在時頻域內對小波變換后的時頻譜值擠壓和重排,信號的瞬時頻率更加接近真實頻率,提高了信號時頻分析的時頻聚焦能力。2017年Yu等[8]拓展短時傅里葉變換(STFT)窗函數,提出了改進短時傅里葉變換,分辨率更為集中。但是,它仍受到海森堡不確定性原理的制約以及原因不明的交叉項影響。據此,在同步擠壓算法的啟發下,將改進短時傅里葉變換(GSTFT)與同步擠壓變換算法進行結合,發展了同步擠壓改進短時傅里葉變換(SSTFT)。
參考前人研究成果,本文結合同步擠壓改進短時傅里葉變換與相干算法,利用同步擠壓改進短時傅里葉變換的高時頻聚焦能力,對南海某工區的三維地震數據體進行頻譜分解,得到不同頻率的單頻數據體;然后應用多道傾角導向相干技術計算單頻數據體。結果表明,該方法可精細刻畫微小斷裂或裂縫發育區,驗證了該方法的準確性及實用性。
1 技術與原理
1.1 短時傅里葉變換
傅里葉變換是一項實用且強大的時頻分析工具,但對地震等非平穩信號開展時頻分析時,僅利用傅里葉變換達不到理想的分辨率。短時傅里葉變換是在傅里葉變換的基礎上使用窗函數截斷非平穩信號,此時可以將窗函數內的信號看作平穩信號,再對該信號做傅里葉變換。以此類推,對全部截斷的信號分別做傅里葉變換,可以得到二維時頻譜圖[9-15]。
假設信號x(t)屬于實數域平方可積函數空間,則其短時傅里葉變換表達式為

(1)
式中:f為頻率;τ為時窗中心;i為虛數單位;g(t-τ)為窗函數。當短時傅里葉變換的窗函數確定后,分辨率也隨之確定,即短時傅里葉變換的分辨率是唯一的。
將式(1)離散化可得到離散短時傅里葉變換
(2)
1.2 改進短時傅里葉變換
由于傳統的短時傅里葉變換分辨率由窗函數確定,因此它的分辨率固定,無法滿足地震數據高分辨率處理的要求。改進短時傅里葉變換窗函數得到新的短時傅里葉變換公式,由式(1)分別對信號和窗函數求復共軛,得到


(3)
(4)
令t-r=r′,則

(5)
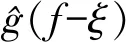
(6)
改進短時傅里葉變換為
(7)
1.3 同步擠壓改進短時傅里葉變換
根據式(7),對GSTFT的時間t求導,則
=GSTFT(t,f)if0
(8)
可得信號的瞬時頻率
(9)
根據式(9),可得同步擠壓改進短時傅里葉變換

(10)
式中:η為同步擠壓改進短時傅里葉變換后的時頻譜頻率;δ為同步壓縮算子。
由式(10)可知,將某一時間點所對應的頻譜值累加到某一瞬時頻率上,可提高信號的時頻分辨率。經合成的理論信號分析結果驗證,SSTFT具有高時頻聚焦能力。
1.4 多道傾角導向相干技術
實際地質體都存在一定的傾角和方位角,而傳統的相干技術是沿著地震網格方向計算相干值。因此,傳統的相干算法不能很好地處理地震信號的方向特征[16],相干算法的計算路徑無法與地層傾角保持一致。基于此,如果不考慮地層的傾角,相干體結果的精度將會受到嚴重影響,甚至會是錯誤的(通常會造成斷裂模糊、尖滅點不清楚等現象)[17-19]。多道傾角導向相干技術是利用多條地震道的信息計算某一點的相干值,并且在傾角估算時采用多窗口方法,使該技術對斷裂的刻畫更加清晰[20]。
2 應用效果
2.1 時頻效果分析
首先利用線性調頻信號檢驗算法的可靠性。合成信號是由兩個線性調頻信號疊加而成
(11)
圖1a為原始合成信號,圖1b是對圖1a信號作短時傅里葉變換得到的時頻譜。由圖可見,短時傅里葉變換的時頻分辨率不高,同時,由于短時傅里葉固定時窗,導致時頻譜末端拉伸。圖1c是對圖1a信號作改進短時傅里葉變換得到的時頻譜,發現改進短時傅里葉變換的時頻分辨率較高,但仍然無法擺脫海森堡不確定性原理的限制以及原因不明的交叉項的干擾。由此可見,改進短時傅里葉變換與短時傅里葉變換同樣存在對信號分析時頻分辨率不佳的局限。圖1d是對圖1a信號作同步擠壓改進短時傅里葉變換得到的時頻譜,對比圖1d與圖1b、圖1c可知,同步擠壓改進短時傅里葉變換具有最高的時頻分辨率,能清晰地刻畫信號的瞬時頻率,并且克服了短時傅里葉變換固定時窗的局限。
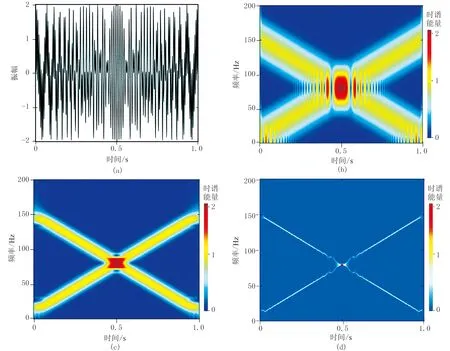
圖1 合成信號及不同算法得到的時頻譜
2.2 抗噪性研究
實際采集的地震數據存在大量噪聲,即使進行降噪處理,但仍然無法完全消除噪聲,因此,要求對地震數據時頻處理的方法具有一定的抗噪性。對圖1a合成信號添加隨機噪聲,分別采用STFT、GSTFT、SSTFT算法處理,得到的時頻譜如圖2所示。
圖2a為原始加噪信號。圖2b是對圖2a作短時傅里葉變換得到的時頻譜,可見短時傅里葉變換受噪聲影響很大,有效信息被噪聲淹沒,無法清晰地看出信號的時頻分布。圖2c是對圖2a加噪信號作改進短時傅里葉變換得到的時頻譜,時頻分辨率較短時傅里葉變換得到了很大的提高,受噪聲的影響非常小。由此可見,改進短時傅里葉變換具有更高的抗噪能力。圖2d是對圖2a加噪信號作同步擠壓改進短時傅里葉變換得到的時頻譜,有效信息幾乎不受噪聲的影響,具有一定的抗噪性,在含噪的信號中仍然可以得到分辨率很高的時頻分析結果。
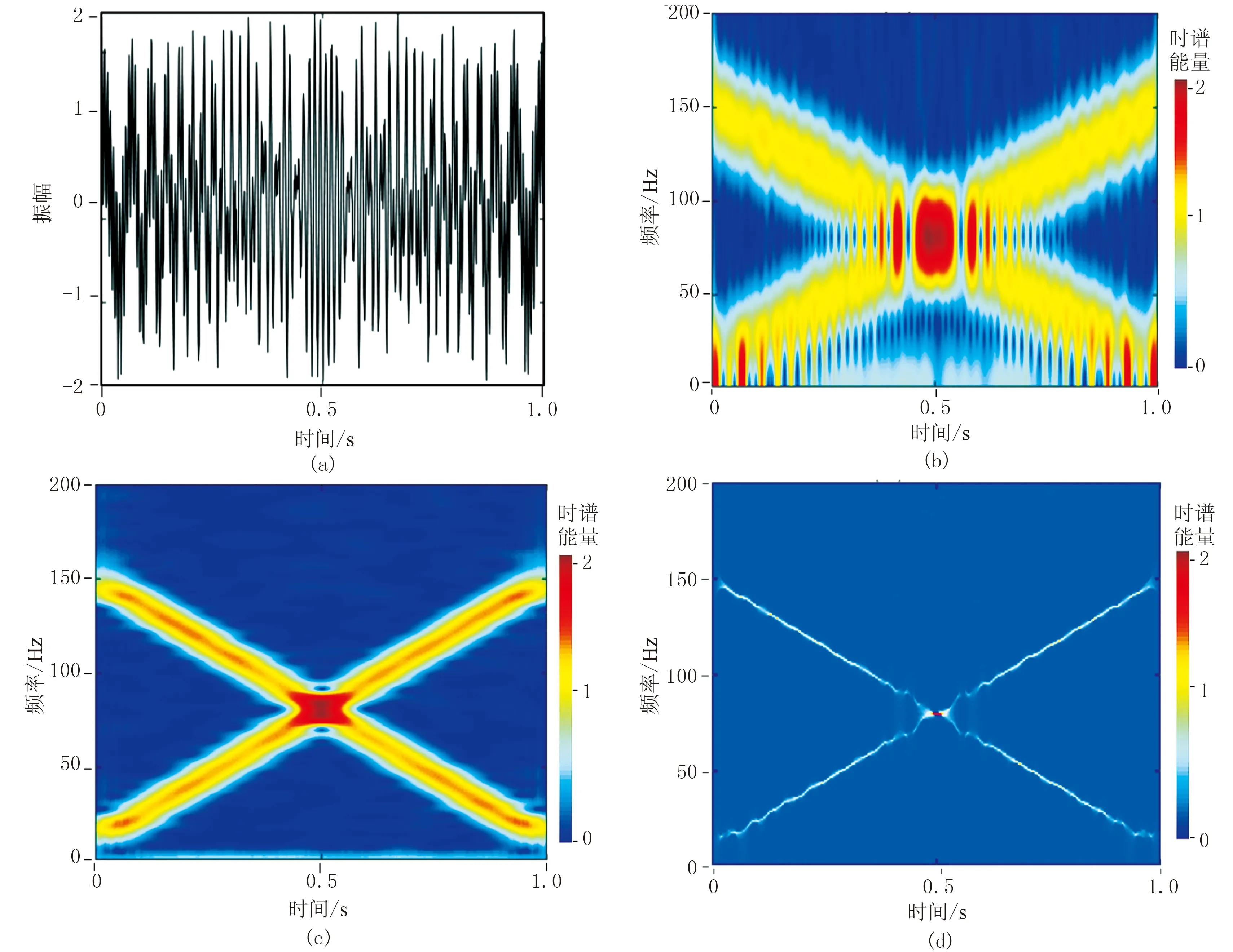
圖2 加噪信號及不同算法得到的時頻譜
2.3 多道傾角導向相干技術應用
南海海上某工區處于油氣開發階段,需要精細刻畫小斷裂及裂縫發育區。但前期處理的地震資料分辨率低,無法識別小斷裂及裂縫發育區。為了滿足不同級別斷裂的識別需求,本文采用同步擠壓改進短時傅里葉變換方法對地震資料進行分頻處理。在分頻處理時,頻率的選擇尤為重要。為此提取井旁地震道作時頻變換處理,確定地震資料的優勢頻帶范圍。采用短時傅里葉變換和同步擠壓改進短時傅里葉變換得到井旁地震道的時頻譜如圖3所示。
由圖3紅色虛線框內圖像可知優勢頻帶為25~63Hz。在優勢頻帶范圍內,采用同步擠壓改進短時傅里葉變換對原始三維地震資料作分頻處理,分別得到25、30、40、60Hz的單頻數據體,然后利用多道傾角導向相干技術進行相干計算,得到單頻相干數據體。
對比25、30、40、60Hz四個頻率的相干屬性剖面(圖4)可見,隨著頻率的增加,相干屬性剖面中所反映出的地質信息也會隨著改變。25Hz的低頻相干剖面中,可識別較大尺度斷裂;30Hz與40Hz的中頻剖面中,不僅可見斷裂整體展布特征,還可識別某些中尺度的斷裂(圖4b、圖4c紅色虛線框內);而60Hz的高頻剖面中,則可見小斷裂及裂縫發育區(圖4d紅色虛線框內)。
對單頻相干數據體提取沿層切片,得到結果如圖5所示。圖5a為低頻相干切片,可以用于刻畫較大斷裂;圖5b、圖5c為中頻相干切片,可用于識別中尺度的斷裂,如紅色虛線框紅色箭頭所示的中尺度斷裂在低頻相干切片中顯示不清晰,因此,中頻相干切片對由大斷裂所控制的中尺度斷裂信息更為敏感;而高頻相干切片中所反映的信息更為豐富,如圖5d紅色虛線框紅色箭頭所示,它不僅可以凸顯微小斷裂,還可以識別伴生裂縫發育區。

圖3 井旁地震道及不同算法得到的時頻譜
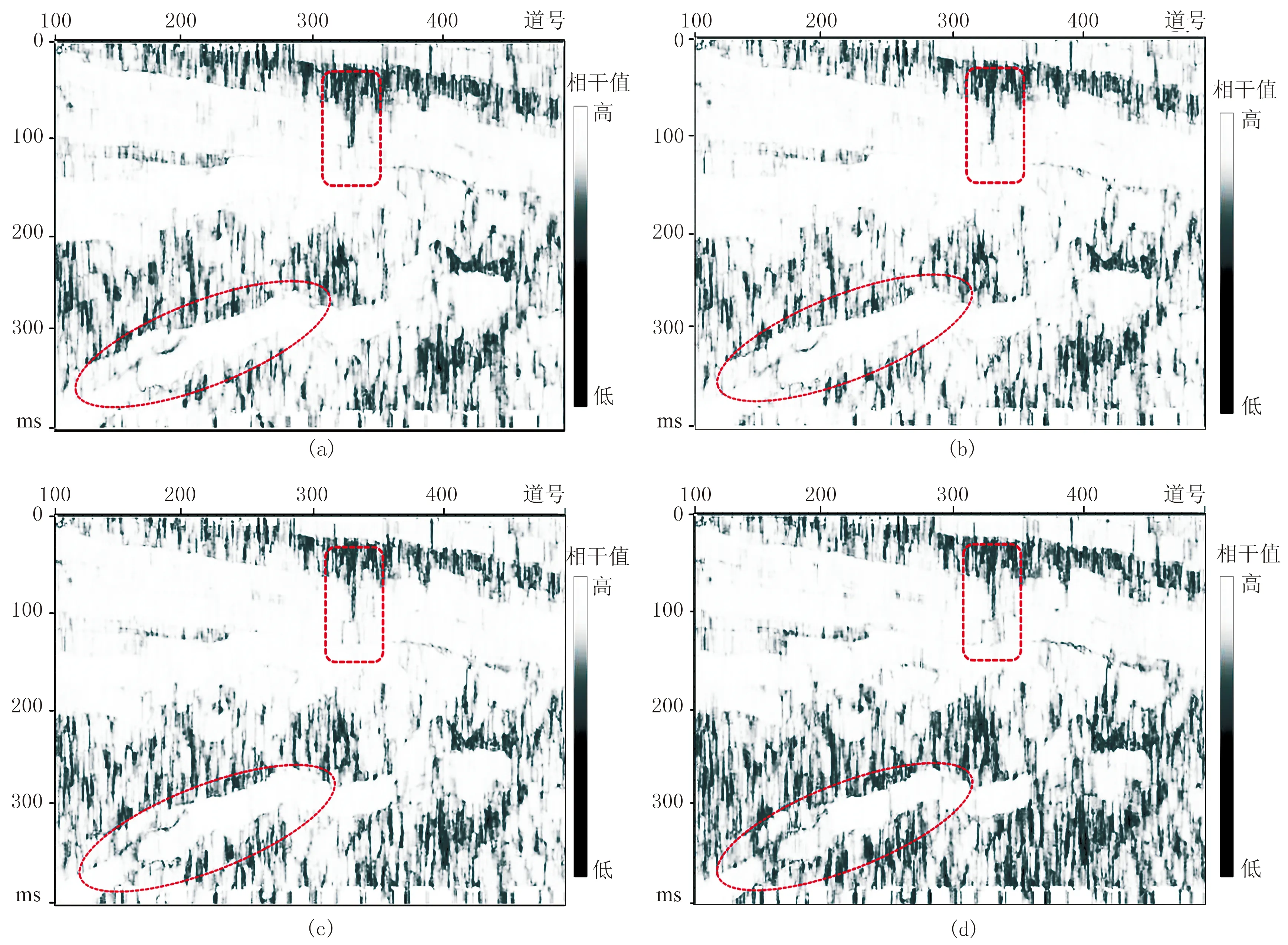
圖4 單頻相干屬性剖面
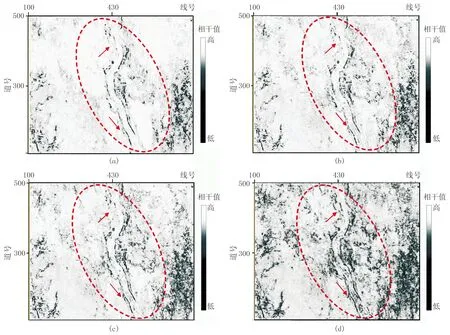
圖5 單頻相干屬性沿層切片
3 結束語
運用基于同步擠壓改進短時傅里葉變換分頻多道傾角導向相干技術處理南海某工區地震數據體,結果表明,得到的單頻數據體可以反映與原始數據體不同的地質體邊緣信息;在此基礎上計算得到的單頻相干屬性可以識別不同級別的斷裂。該方法不僅具有同步擠壓改進短時傅里葉變換的高時頻分辨率的優勢,而且還有多道傾角導向相干技術準確識別斷裂的優點。

