利用數據低秩性和稀疏性的位場分離

朱 丹 劉天佑* 李宏偉

(①中國地質大學(武漢)地球物理與空間信息學院，湖北武漢 430074；②中國地質大學(武漢)數學與物理學院，湖北武漢 430074)

0 引言

在應用科學和工程領域，觀測的數據集往往是高維的，提取高維數據的低秩結構尤為重要[1]。主成分分析(Principal Component Analysis,PCA)作為一種經典的低秩矩陣逼近方法被廣泛應用。對于被獨立同分布的高斯噪聲污染的觀測數據，經典PCA往往能夠給出低秩矩陣逼近問題的最優解，然而對于被高度污染的數據(如有色噪聲)卻難以準確估計[2]。

為了解決數據被高度污染的低秩矩陣逼近問題，Candes等[3-5]提出魯棒主成分分析(Robust Principal Component Analysis,RPCA)。該方法在經典PCA的基礎上，將原來求解噪聲矩陣Frobenius范數極小化的數學模型，拓展到求解低秩成分矩陣的秩和噪聲矩陣的L0范數極小化的數學模型。基于合理的數學模型，RPCA迅速成為圖像處理和數據挖掘領域的研究熱點。針對RPCA數學模型的優化問題，許多學者進行了研究。史加榮等[6]采用迭代閾值算法(Iterative thresholding,IT)求解其提出的數學模型。該算法具有迭代形式簡單且收斂的優點，但是由于收斂速度慢及難以選取步長，所以應用范圍有限。Lin等[2]采用加速近端梯度算法(Accelerated proximal gradient,APG)求解RPCA的數學模型。與IT算法相比，APG算法迭代次數大大降低。Lin等[2]提出精確拉格朗日乘子(Exact augmented Lagrange multipliers,EALM)法和不精確拉格朗日乘子(Inexact augmented Lagrange multipliers,IALM)法。實踐證明，EALM和IALM法具有更高的計算效率和精度[6]，因而逐漸成為求解RPCA數學模型的主流算法。本文采用EALM求解RPCA數學模型。

重磁場是由具有不同密度和磁性的地質體的共同響應，即不同尺度、不同幅值異常的疊加。如何從混疊重磁場中分離出目標地質體引起的異常，是重磁數據處理的重點之一。

位場的識別與分離方法包括解析延拓、滑動平均、趨勢分析、匹配濾波、插值切割以及近年發展起來的小波分析、最小曲率等[7-8]。Spector等[9]推導了航磁異常的能譜公式，提出利用能譜分析粗略估計塊狀體埋深的方法，并在1975年提出匹配濾波法分離重磁場；程方道等[10]提出插值切割法分離磁異常；Mickus等[11]首次將最小曲率法應用于美國某地區的布格重力異常分離；王萬銀等[12-13]研究了位場數據最小曲率擴邊和補空方法；隨著小波分析法的提出，Fedu等[14]、侯遵澤等[15]和楊文采等[16]提出一種基于離散小波變換的重磁位場分離方法。

現有的位場分離方法往往會出現參數難選擇、分離效果差、虛假異常等情況，這不僅會造成主觀上地質認識的錯誤，還給后續反演解釋帶來偏差。因此，精度高、自適應性強、應用簡單的位場分離方法是最佳選擇。朱丹等[17]提出基于奇異譜分析的位場分離方法，該方法先將位場數據表示成Hankel矩陣(原始數據是一維的情況)或塊Hankel矩陣(原始數據是二維的情況)，然后利用PCA或EOF(經驗正交函數分解，empirical orthogonal functions)實現數據降維，從而達到區域場與局部場分離的目的。

本文RPCA是信號處理領域的一種新方法。利用RPCA實現Hankel矩陣或塊Hankel矩陣的降維，RPCA可有效處理低秩矩陣逼近問題，其特點是參數設置簡單、結果穩健。本文主要研究RPCA在位場分離中的應用，介紹經典PCA和RPCA的數學模型，并從位場的低秩性和稀疏性的角度分析位場分離問題；利用EALM算法求解RPCA數學模型，并提出針對一維信號的RPCA處理方法；通過理論模型展示分離效果及參數的選取方式，并將本文方法應用于實際數據處理。

1 PCA和RPCA的數學模型及EALM求解方法

假設有一高維的數據嵌套在低維線性子空間中，那么PCA和RPCA的目標就是高效且準確地提取這個低維子空間。

1.1 數學模型

假定已知一混疊低秩和高秩成分的觀測矩陣D∈Rm×n，為了提取D的低秩成分，將D分解成矩陣A和E，這里A是低秩矩陣，E是服從獨立同高斯分布的矩陣。那么通過PCA估計A和E可歸結為求解最優化問題

(1)

式中‖·‖是Frobenius范數，其定義為

(2)

可利用奇異值分解D=UΣVT計算上述數學模型，確定r個主奇異值以及對應的左奇異向量。這r個主奇異值反映了信號的主要特征，并通過這r個主奇異值和奇異向量可以恢復出低秩矩陣A。

然而，若E是非獨立同高斯分布矩陣，PCA方法不再適用。此時，將原數學模型修改為雙目標極小的數學模型

(3)

式中‖E‖0是0范數，表示E中非零元素的個數。

從式(3)可以看出，與PCA只考慮‖E‖F極小不同，RPCA的數學模型要求E盡量稀疏、同時又保證了A的低秩性。

對于式(3)的雙目標極小問題，可以引入懲罰函數進行求解

(4)

式中λ是權系數。

由于上述數學模型是一個非凸的優化問題，為便于求解，需要將模型中的目標函數進行松弛處理[6]

(5)

式中‖·‖1,1和‖·‖*分別表示(1,1)范數和核范數，分別定義為

(6)

‖A‖*=max[trace(UTAV)∶

UTU=Im,VTV=In]

(7)

式中trace(·)表示求矩陣的跡。

1.2 EALM算法

在介紹EALM算法之前，先引入兩類優化問題及其最優解[2]。

令Q=(q1,q2,…,qn)為m×n維實矩陣，則優化問題

(8)

的最優解為P*=Sε(Q),Sε(Q)是關于參數ε、Q的函數，表示Q的第(i,j)元素經max(|qi,j|-ε,0)×sgn(qi,j)變換得到新的矩陣P*的第(i，j)元素，其中參數ε>0，且Sε(Q)=εS1(Q/ε)。

對于優化問題

(9)

有閉形式解P*=Dε(Q)，其中Dε(Q)=USε(Σ)VT，UΣVT是矩陣Q的奇異值分解，并且Dε(Q)=εD1(Q/ε)。

下面使用EALM求解式(5)。構造增廣拉格朗日函數

L(A,E,Y,μ)=‖A‖*+λ‖E‖1,1+

(10)

交替迭代A、E和μ，直到滿足收斂條件或達到最大迭代次數為止，其計算流程如下。

(1)輸入觀測矩陣D∈Rm×n和權系數λ。

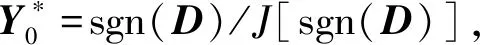
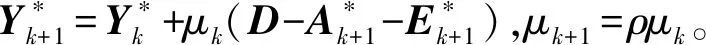
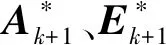
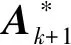
1.3 位場數據的延滯矩陣構建

秩的概念是針對矩陣而言的，對于重磁勘探一維觀測數據，把它表示成空間延滯矩陣，即對一維數據Hankel矩陣化，對于二維觀測數據，則構建塊Hankel矩陣。對數據進行重排列的原因是延滯矩陣具有低秩結構[18]。

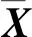
(11)

若有二維矩陣X=[xi,j]∈Rp×q，其中xi,j表示矩陣X的第i行第j列的元素。利用X的第l列構建Hankel矩陣

(12)

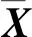
(13)

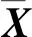
1.4 實現步驟

RPCA的位場分離方法包括下列3個步驟。

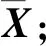
(2)利用RPCA實現矩陣降秩。選取合適的權參數構建雙目標優化模型，并利用EALM算法求解低秩矩陣A和稀疏矩陣E。

(3)數據重構。步驟(2)中得到的低秩矩陣A和稀疏矩陣E是近似Hankel矩陣或近似塊Hankel矩陣的結構，因此需要將其恢復成嚴格的Hankel矩陣或塊Hankel矩陣。對于一維數據，采用逆對角線平均的方法；對于二維數據，先求式(13)的逆對角線上的Hankel矩陣的平均，再求各Hankel矩陣的逆對角線平均。最后，將Hankel矩陣或塊Hankel矩陣恢復成數據向量或矩陣。

2 區域場的低秩性與局部場的稀疏性

矩陣秩定義為該矩陣中線性無關的行數或列數。考慮矩陣A∈Rm×m是一個方陣，其秩是矩陣A的非零特征值的個數。當A不是方陣時，即矩陣A∈Rm×n，其中m≠n，其奇異值分解A=UΣVT，且Σ=diag(σ1,σ2,…,σr,0,…,0)，其中σi是奇異值，那么矩陣A的秩是非零奇異值的個數。若rank(A)?min(m,n)，那么稱矩陣A是低秩的。

稀疏性描述的是矩陣中非零元素的個數，大多數元素為零的向量或者矩陣稱為稀疏向量或稀疏矩陣[1]。考慮矩陣E∈Rm×n，若‖E‖0?mn,那么稱矩陣E是稀疏的。實際情況中，區域場具有低秩性，局部場具有稀疏性，即位場的分離問題符合RPCA的數學模型。

下面解釋區域場的低秩特征。通常能夠利用數據間的相關性說明矩陣秩的大小，因為矩陣不同列之間的相關性差異往往能夠反映矩陣秩的差異。考慮一種極端的情況，當矩陣中每一列都是線性無關時，該矩陣為滿秩矩陣，若其中某些列是線性相關時，經過初等變換，那么可以使其中部分列變換成零向量，這時該矩陣是低秩的。

區域場通常變化平緩，其相鄰觀測點之間具有較強的相關性。由此，區域場的延滯矩陣的相鄰列之間的相關性更強，矩陣具有更低秩的特征。統計學上采用自相關系數描述這種自相關性

(14)

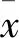
通過理論模型對比進一步說明區域場的低秩性。將由淺部規模較小場源引起的小尺度異常視為局部場(圖1a)，將由深部規模較大場源引起的大尺度異常視為區域場(圖1b)。對比區域場、局部場和高斯白噪聲的自相關系數(圖2)可以看出，區域場自相關性強，局部場次之，噪聲不具有自相關性。因此區域場通過滑動窗口構成的延滯矩陣不同列之間具有較強的相關性，局部場的延滯矩陣不同列之間具有較弱的相關性，而噪聲的延滯矩陣不同列之間不具有相關性。因此，從圖3可以看出，區域場延滯矩陣比局部場延滯矩陣的非零奇異值少，噪聲延滯矩陣的奇異值幾乎全大于0。這說明區域場延滯矩陣的秩低于局部場，噪聲延滯矩陣是滿秩的。

與低秩性相比，稀疏性相對容易理解。實際應用中，向量或矩陣中的元素通常不會嚴格等于0，因此利用接近于0的元素或明顯大于0的元素個數描述矩陣的稀疏性。深部規模大的場源引起的異常往往是大尺度的，一般會覆蓋整條剖面或測區，因此異常值明顯大于0的觀測點個數較多，具有非稀疏性或較弱的稀疏性。對于淺部小規模場源，即使具有較大的磁化強度和剩余密度，隨著觀測點遠離場源，它引起的異常會迅速衰減，因此僅很小的范圍內位場數據數值的絕對值明顯大于0。相比于區域場，局部場的稀疏性更強，并且兩者稀疏性的差異通常是顯著的。

圖1 磁場模擬

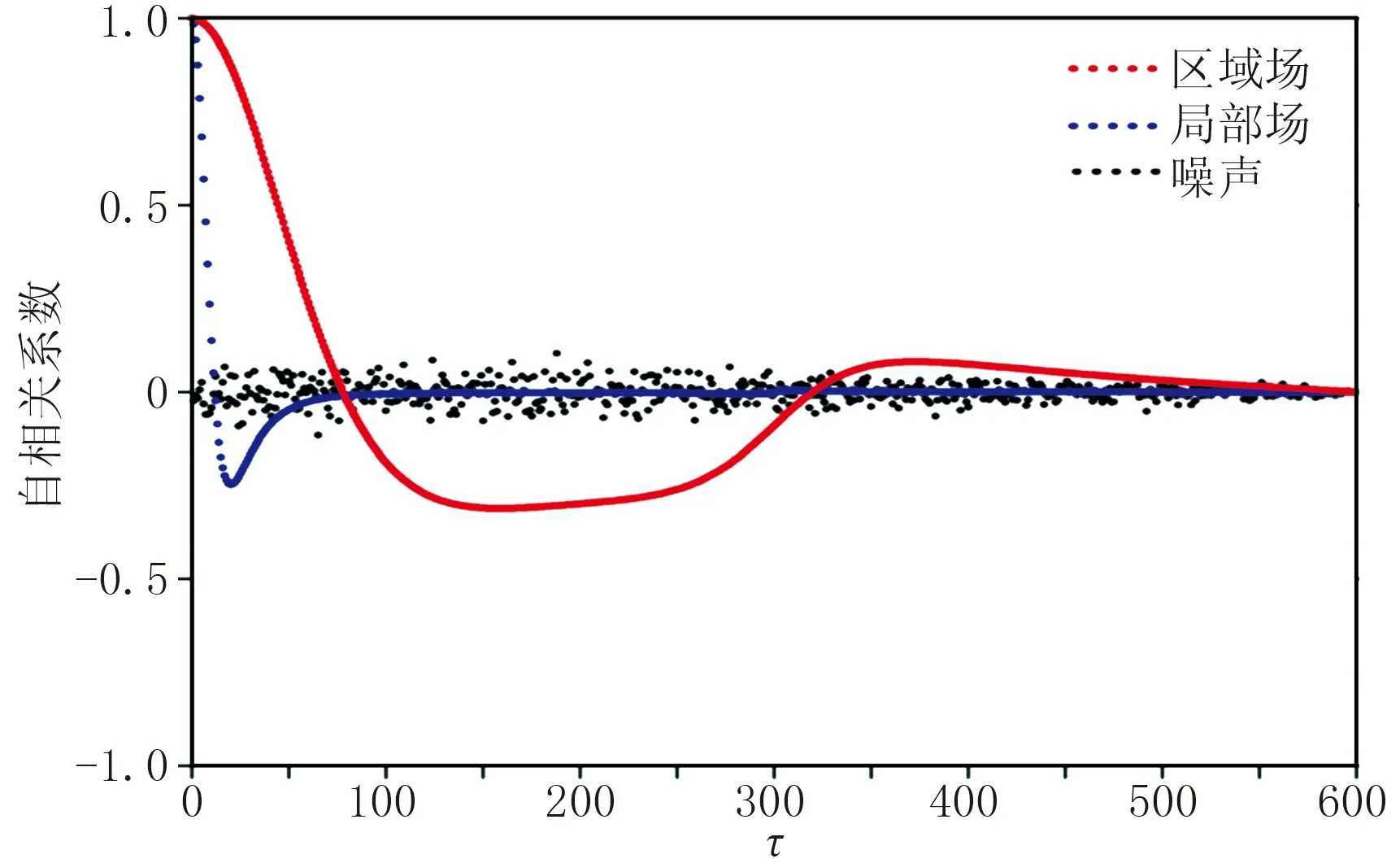
圖2 區域場、局部場和噪聲的自相關系數

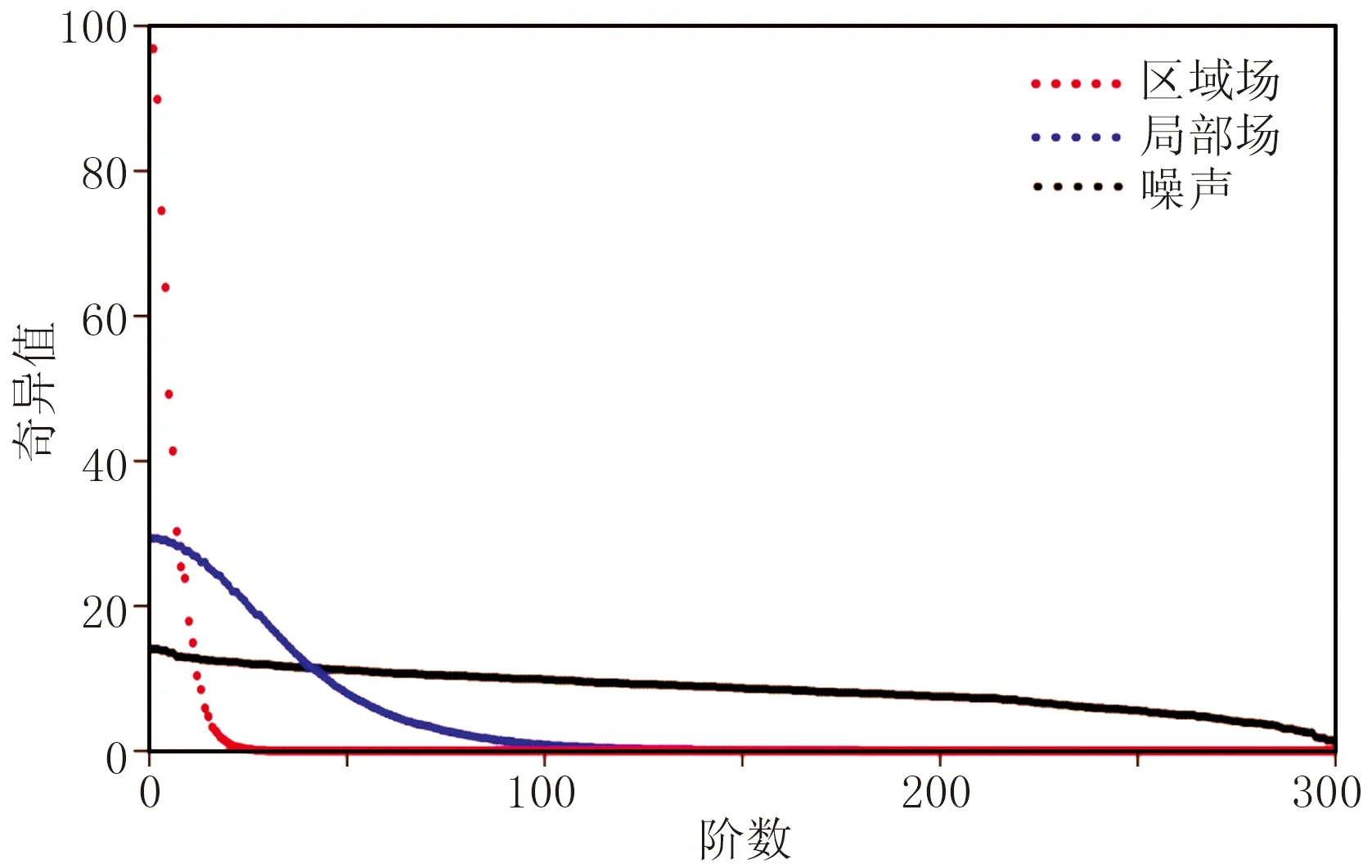
圖3 區域場、局部場和噪聲的奇異值

3 RPCA數學模型的地球物理意義

前面的分析說明尺度較大的異常具有低秩的結構，尺度較小的異常具有稀疏的結構，即區域場是低秩的，局部場是稀疏的。從區域場的逼近程度理解位場分離問題，在分離位場時往往會出現區域場的欠擬合和過擬合問題。欠擬合現象實質就是分離得到的區域場不夠低秩而局部場過分稀疏；過擬合現象的實質是分離得到的區域場過于低秩導致局部場不夠稀疏。利用傳統位場分離方法(如匹配濾波或小波分析等)分離位場數據時，往往存在穩定性較差的問題，即參數選擇的微小改變使分離結果變化顯著。例如，估計對數功率譜低頻線性段的斜率時，極小的估計誤差就會帶來深部場源似深度估計的巨大誤差，這容易導致位場分離結果的欠擬合或過擬合。小波分析的應用難點在于選擇哪一階或哪幾階細節疊加構成局部場或區域場。然而，RPCA的數學模型要求E盡量稀疏的同時又保證了A的低秩性，這使系統具有更強的魯棒性，即分離結果更穩定并且更容易避免欠擬合或過擬合現象。因為當分離的局部場過分稀疏(欠擬合)時，區域場低秩的結構被破壞并導致區域場的核范數增加；而當分離的區域場過分低秩(過擬合)時，局部場稀疏的結構被破壞并導致局部場的(1,1)范數增加。因此，RPCA數學模型的地球物理意義在于:在保證分離區域場盡可能低秩的前提下局部場盡可能的稀疏，并且，當區域場的低秩性結構和局部場的稀疏性結構被破壞時，其對應的核范數和(1,1)范數會快速增加。因此，采用RPCA分離位場很容易達成一種相對穩態，這種穩態體現在權系數變化時，分離結果幾乎不變。處于這種穩態時的分離效果最佳。

4 權系數的選擇

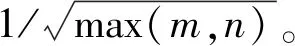
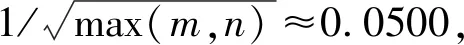
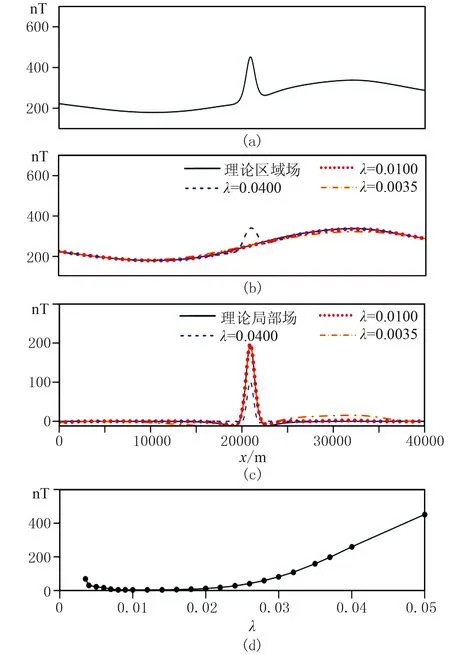
圖4 權系數與分離誤差的關系

5 理論模型計算

匹配濾波和小波分析是位場分離中的常用方法。匹配濾波是一種地質意義明確的位場分離方法，其基本原理是埋深不同的兩種場源在對數功率譜曲線上表現出不同梯度的線性下降特征，利用這種特征的差異構制濾波器，能夠分離上下疊加的地質體的場[7,19]。小波分析能夠將重磁場精細地分解到不同尺度的細節上，這些不同尺度的細節反映不同尺度和深度的場源，常被用于位場的分解和分析[15-16,20-21]。本文通過理論模型計算對RPCA與這兩種方法進行對比。

5.1 RPCA與匹配濾波法的對比

通過理論模型1(圖5d)對比RPCA與匹配濾波分離法。模型正演設定256個觀測點，分別對總場(圖5a)、理論區域場(圖5b)和局部場(圖5c)進行離散傅里葉變換并求取其對數功率譜。圖6是非負頻率對數功率譜，每條曲線共129個離散對數功率點。根據Spector等[9]提出的方法，分別在對數功率譜的低頻段和中高頻段的近似線性下降部分取切線，并通過兩條切線的斜率及在縱軸上的截距構建區域場和局部場濾波器，最終得到的分離結果如圖7所示。與理論場相比，匹配濾波分離的局部場多余了一部分低頻成分而區域場缺失了一部分低頻成分(圖7a和圖7b中藍色虛線部分)，說明分離結果與理論值不吻合。

分離效果較差的原因主要有以下幾點： ①區域場頻譜的能量過于集中于低頻段，導致只能利用很少的頻率點判斷切線位置。②由于局部場在低頻段同樣具有較強能量，并且位場具有頻率疊加性，因此局部場的低頻數據疊加到總場的低頻段，導致總場低頻段能量高于實際區域場的能量，使得估計的切線斜率大于實際值。③匹配濾波法穩定性較差，當低頻段切線的首、尾端點位置選取變化較小時，其計算的斜率值變化大，導致分離結果變化大。

與匹配濾波相比，RPCA的參數估計更為簡單。利用RPCA分離位場時，只需要估計權系數，又由于權系數的取值區間寬松，且當其位于最佳區間時分離結果十分穩定，因此容易選取合適的權系數λ。利用RPCA法分離圖5中理論場，當λ取值為0.03～0.10時，分離結果穩定。因此選取中間值即0.06時的分離結果(圖7紅色虛線)與匹配濾波法分離結果進行對比，發現RPCA分離效果更優。

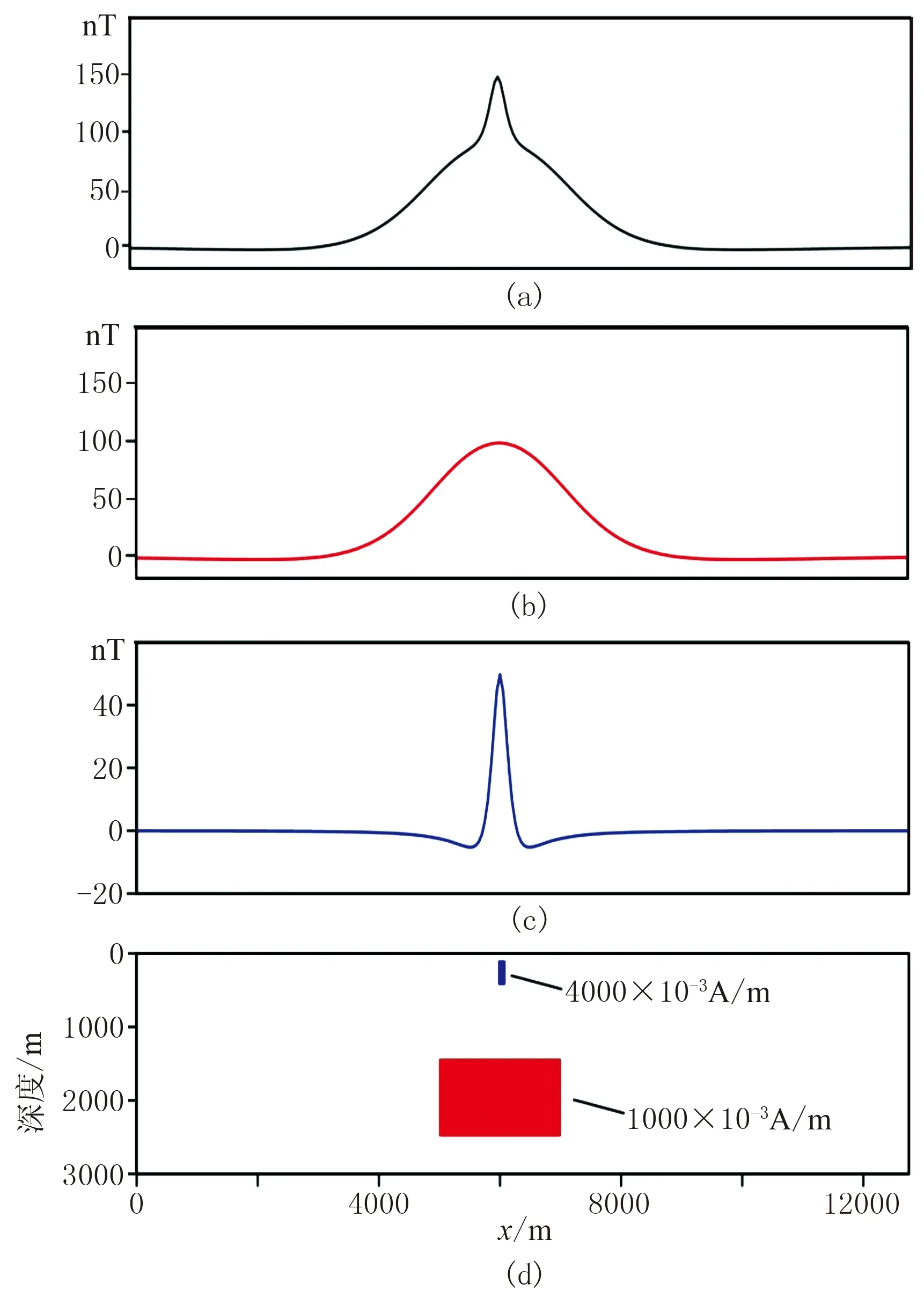
圖5 理論模型1及磁異常

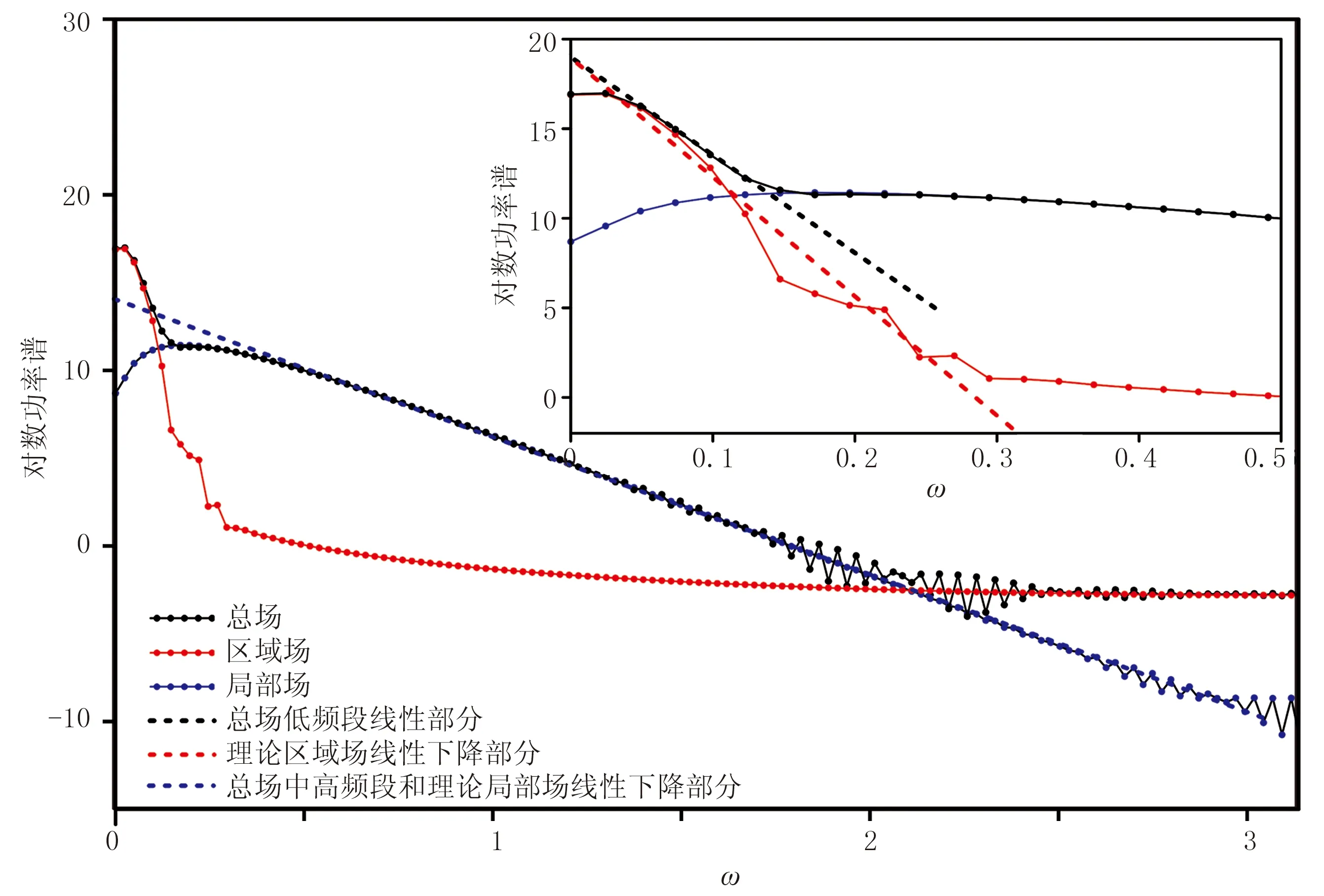
圖6 理論模型1的磁場總場、區域場和局部場的對數功率譜

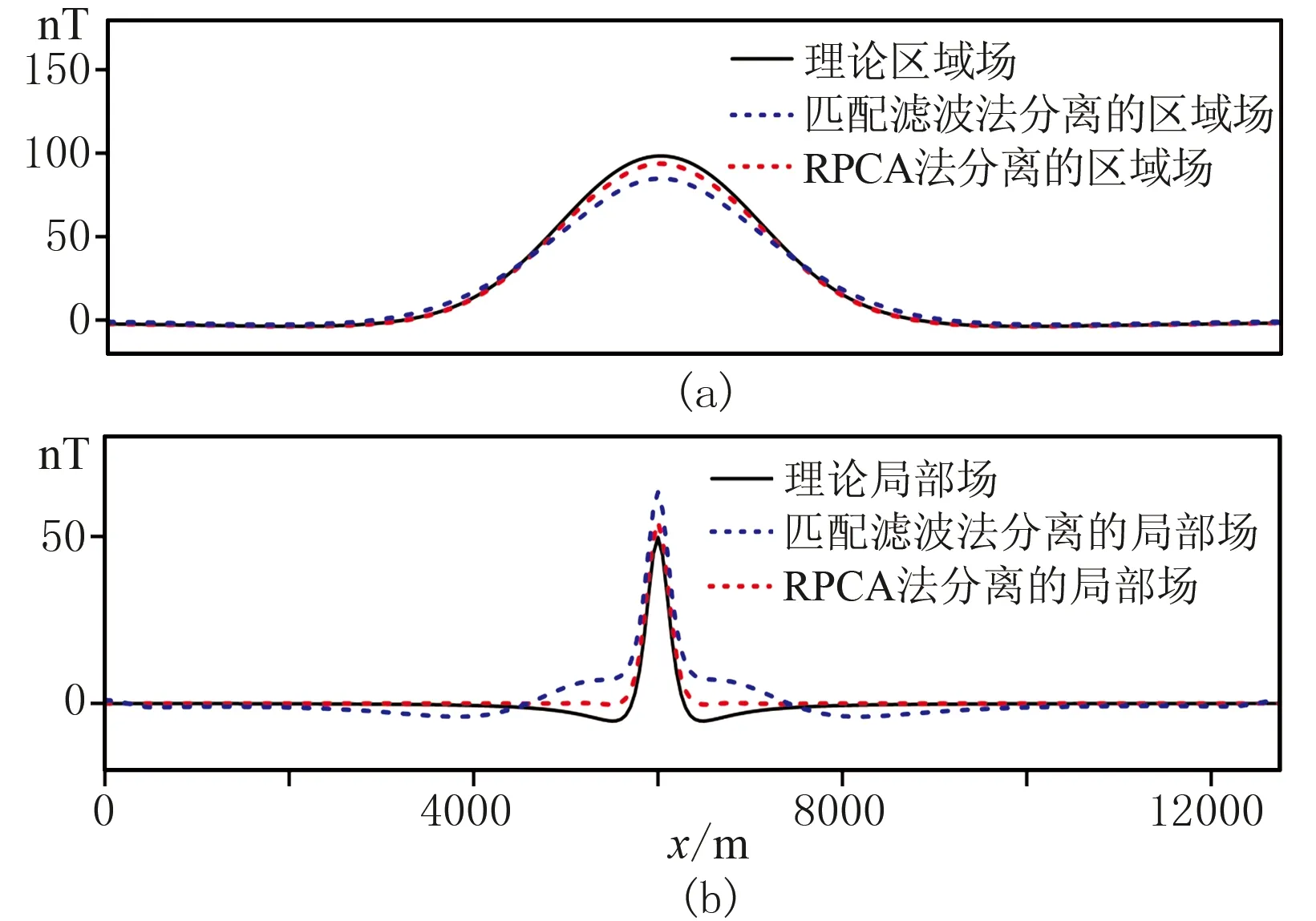
圖7 理論模型1的磁場匹配濾波和RPCA法分離結果

5.2 RPCA與小波分析對比

通過小波分析法將模型1引起的總場異常分成5階細節(圖8a)。可以看出，隨著分解的階數增加，細節尺度逐漸加大。將小波細節1～5階疊加構成局部場，把4階小波逼近作為區域場，得到分離結果如圖8b和圖8c。小波分析法的優勢在于尺度不變性[15-16]，因此應用相對簡單，缺點主要是分解的細節沒有明確的地球物理意義，難以判斷哪幾階細節由局部場引起，哪階逼近由區域場引起。從理論模型1的分離效果來看，RPCA要優于小波分析。

為了對比RPCA與小波分析法在復雜模型情況下的分離效果，建立如圖9f所示模型。總場由三部分構成，分別是深部模型的響應、淺部模型的響應和高幅值隨機噪聲。調節λ，發現λ在0.1200～0.2000時，分離結果穩定。選取λ為0.1700分離總場，得到的噪點如圖9e所示。對剩余場繼續分離，當權系數在0.0200～0.0400變化時，分離結果是穩定的，因此選取權系數0.0300繼續分離剩余場，得到結果如圖9b和圖9d所示。利用小波分析分離總場，分別采用位場小波基、Daubechies小波簇、Coiflets小波簇、Symlets小波簇、Discrete Meyer小波基、Biorthogonal小波簇等15種小波基、Reverse Biorthogonal小波簇分離總場[22]，不同小波基的分離結果差異較大，其中Symlets小波基分離的區域場誤差最小(均方誤差為5.160nT)，分離的區域場如圖9c中藍色虛線所示。對于高幅值隨機噪點，小波分析法無法分離。可以看出，RPCA法的分離效果(均方根誤差為3.289nT)優于小波分析法。

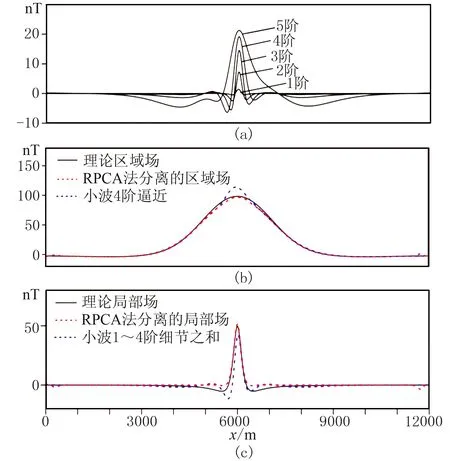
圖8 理論模型1的小波分析和RPCA分離結果

圖9 理論模型及RPCA和小波分析法的分離結果

(a)理論總場；(b)理論區域場和RPCA法分離的區域場；(c)理論區域場和小波分析法分離的區域場；(d)理論局部場和RPCA分離的局部場；(e)噪聲和RPCA分離的噪聲；(f)理論模型

5.3 二維位場數據試驗

建立三維地質模型2(圖10)，其中淺部場源包括不同形狀、不同尺度的4個地質體，深部地質體是一“L”形柱體。此模型的正演重、磁場見圖11。

深部地質體正演區域重、磁異常分別見圖12a、圖12c，淺部地質體正演的局部重、磁異常如圖12b、圖12d所示。采用RPCA算法分離重磁場，當λ取值在0.0020附近變化時，所得的重力分離結果穩定，當λ取值在0.0030附近變化時，所得的重力分離結果穩定。小波分析和匹配濾波的參數選擇原則與實驗1一樣，圖12i～圖12p為兩種方法選擇不同參數得到的最優結果。

重力場的分離中， RPCA、小波分析、匹配濾波的均方根誤差分別是0.016、0.020、0.028mGal。 其中RPCA的分離誤差最小，小波分析殘留了較多深部地質體引起的異常(幅值約為0.05mGal)，匹配濾波分離的局部場的異常幅值遠小于實際局部場異常的幅值。磁場的分離中，RPCA、小波分析、匹配濾波的均方根誤差分別是45.24、60.25、46.94nT，其中RPCA的分離誤差略小于匹配濾波，但小波分析和匹配濾波分離的局部場殘留了部分深部地質體引起的異常(幅值分別是120nT和110nT)。可見復雜模型的重磁場分離中，RPCA的誤差相對較小。

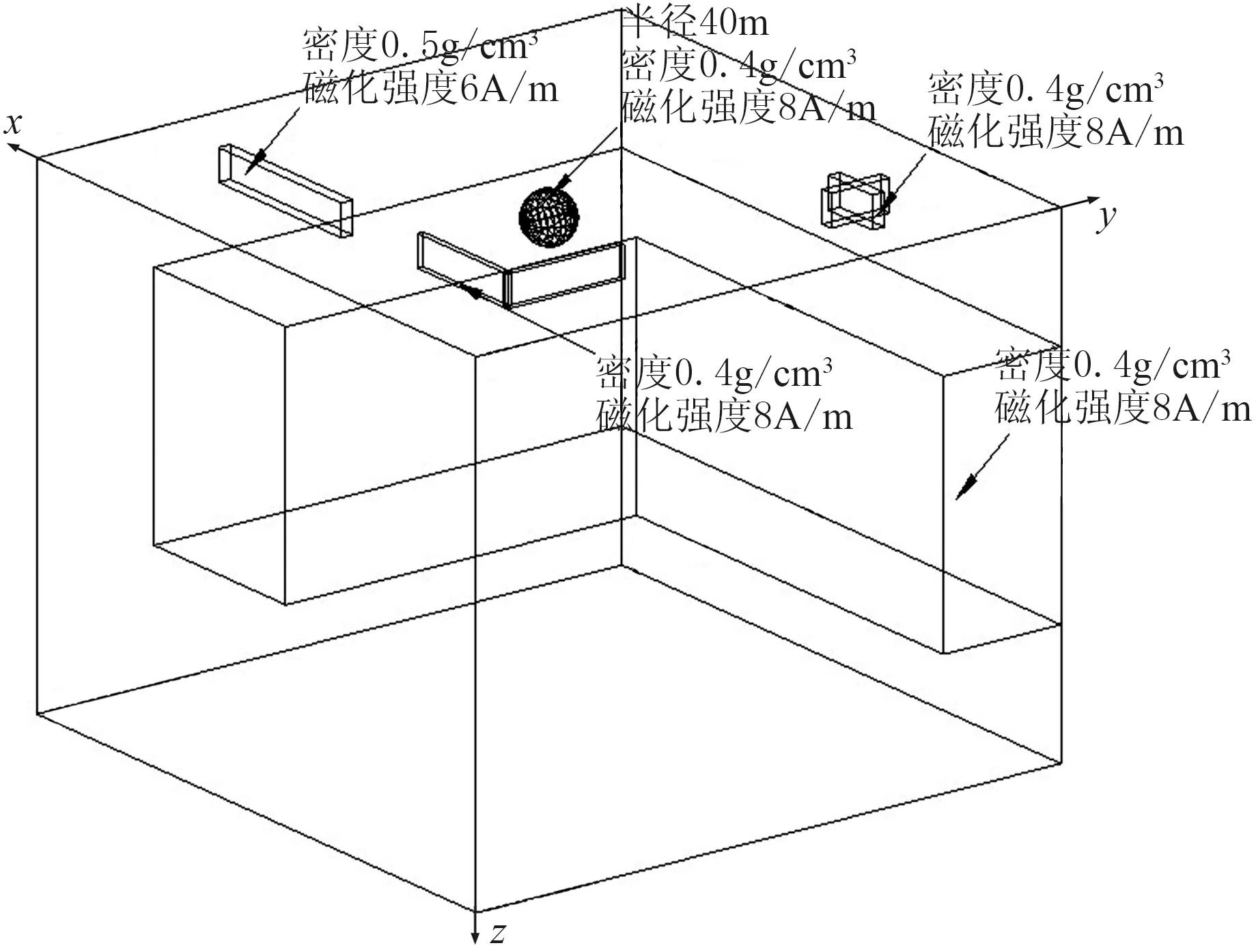
圖10 模型2示意圖

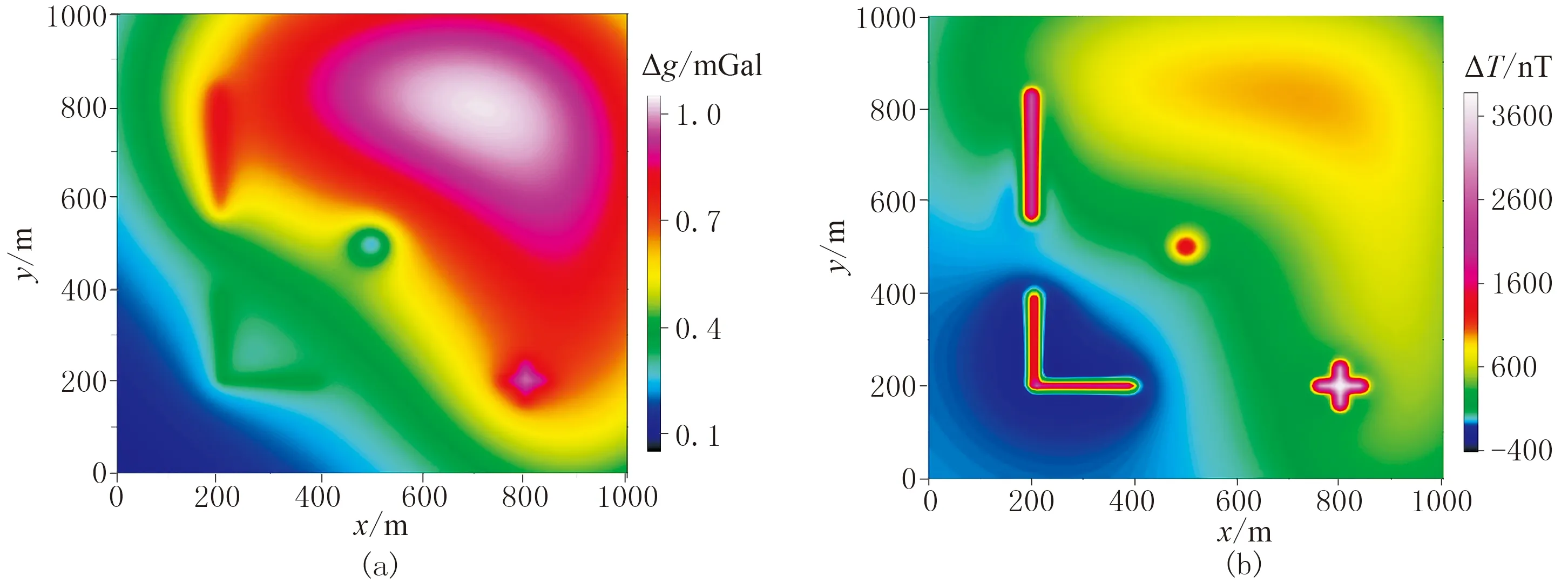
圖11 模型2重(a)、磁(b)異常場正演結果

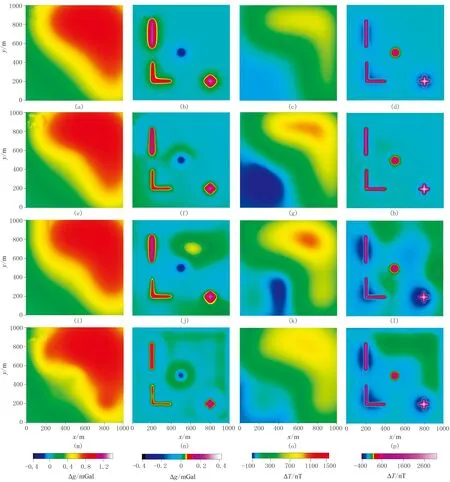
圖12 模型2重、磁場異常圖

(a)～(d)分別為理論計算的區域重力異常、局部重力異常、區域磁異常和局部磁異常；(e)～(h)分別為RPCA法分離的區域重力異常、局部重力異常、區域磁異常和局部磁異常；(i)～(l)分別為小波分析法分離的區域重力異常、局部重力異常、區域磁異常和局部磁異常；(m)～(p)分別為匹配濾波法分離的區域重力異常、局部重力異常、區域磁異常和局部磁異常

6 RPCA應用實例

衛寧北山—香山礦集區位于寧夏西部，大地構造位于北祁連走廊過渡帶，東段位于阿拉善地塊南緣、鄂爾多斯地塊西緣的轉換交界處[23]，是寧夏金屬礦產勘查重要地區之一。衛寧北山位于礦集區的北部，經多年勘查工作，發現多處以金、鉛、銀等為主的金屬礦床，如金場子金礦、照璧山鐵礦、大通溝銅礦等[24]。為此在該地區開展重磁勘探，目的是研究隱伏中酸性巖體的空間侵位特征。

研究區的基底層由早古生代次深海斜坡相陸源碎屑—泥質沉積為主的濁積巖系構成。劉志堅[25]推斷在衛寧北山西部的單梁山西段(二人山—金場子北)及其東部一帶可能存在隱伏的中酸性巖體，與出露地表的閃長玢巖脈很可能為同源、同期形成。

由于區內出露主要以沉積巖為主，因此位場地球物理方法是尋找深部隱伏巖體的有效方法。宋新華等[23]指出，區內基底具有一定磁性，沉積地層(石炭—奧陶系)巖石標本多為無磁性或弱磁性，密度約為2.68g/cm3；巖漿巖體具有磁性，密度為2.60g/cm3。結合物性特征可知，區內巖漿巖體相對圍巖具有低密、高磁的物性特征，由此推斷局部低重、高磁異常主要由隱伏巖漿巖體引起。

研究區布格重力異常和化極磁異常[26]分別如圖13和圖14所示。可見區內布格重力異常為-20～35mGal，呈南低北高趨勢；區內化極磁異常為-60～120nT，北部分布大面積正磁異常。緯度37.55°以北的磁異常均大于20nT，其中以二人山地區磁異常最強，磁異常極大值為120nT；二人山北西部磁異常明顯，極大值約為90nT；二人山東部、北部磁異常較弱，極大值約為50nT。結合物性資料推斷，布格重力異常的區域性變化與致密基底起伏有關，基底的隆起會引起布格重力的升高，隱伏巖漿巖體會引起局部低重異常。化極磁異常主要由磁性基底和巖漿巖體引起，其中磁性基底的磁性較弱且埋深較大，主要引起幅值較低且變化平緩的磁異常，巖漿巖體磁性較強且埋深較淺，主要引起幅值較高且變化快的磁異常。因此，本次研究重點是從布格重力異常和化極磁異常中提取出局部低重、高磁異常，具有局部低重、高磁異常組合特征的區域即是隱伏巖漿巖體的遠景區。

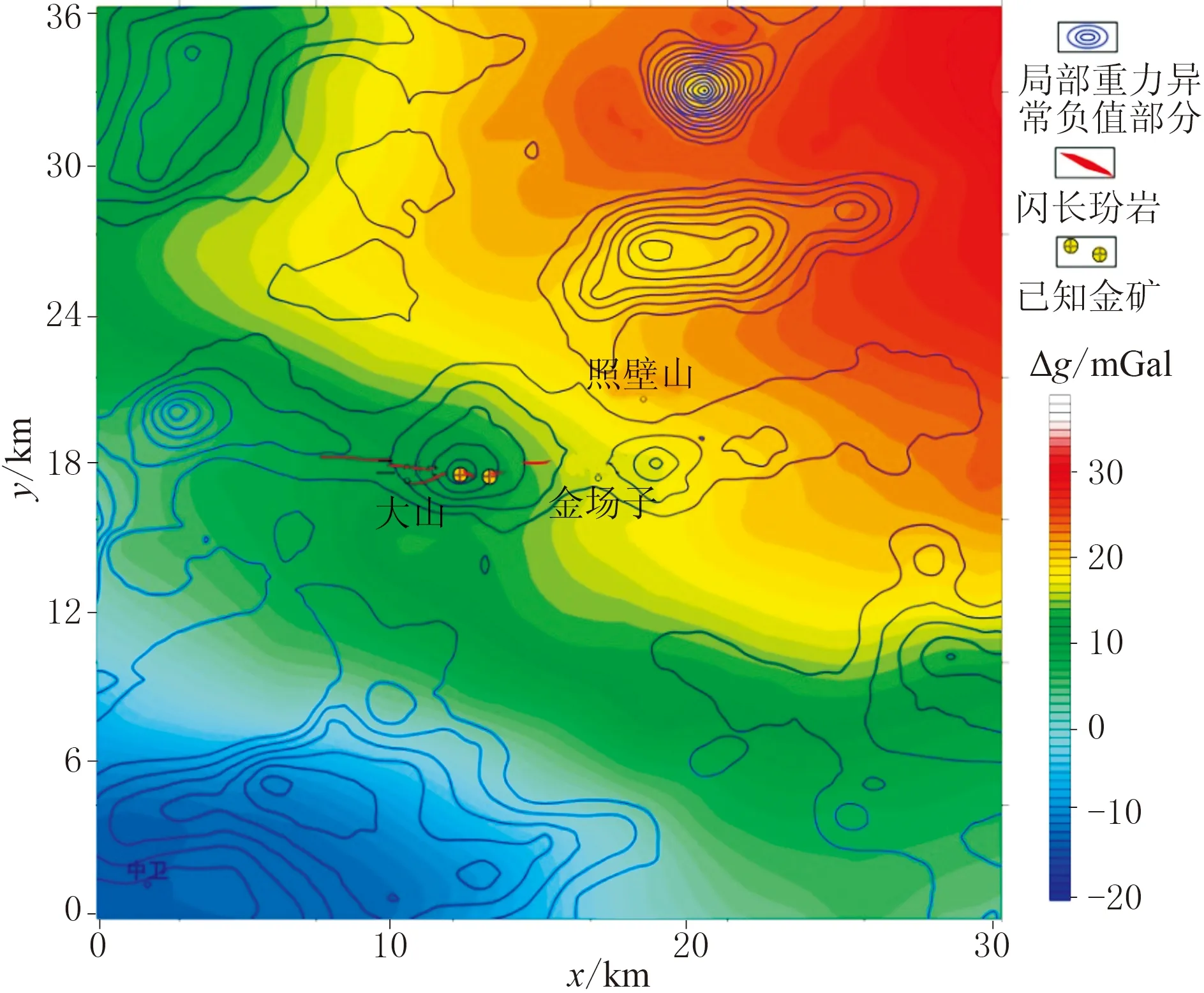
圖13 研究區布格重力異常疊加剩余重力異常圖

利用RPCA法提取局部低重、高磁異常。首先利用RPCA法分離布格重力異常，得到區域重力異常和局部重力異常。當λ取約0.0020時，分離得到的區域重力異常和局部重力異常穩定，其中局部重力異常負值部分如圖13所示。然后利用RPCA法分離化極磁異常，得到區域磁異常和局部磁異常。當λ約為0.0040時，分離的區域磁異常和局部磁異常穩定，其中局部磁異常正值部分如圖14所示。最后，將分離的局部低重異常和局部高磁異常疊合(圖15)，得到7個局部低重高磁異常疊合區(A1～A7)，推斷為隱伏巖體可能賦存的區域。從疊合圖可以看出，二人山地區已知出露的閃長玢巖巖脈與分離的局部低重高磁異常對應關系很好，其中局部低重、高磁異常向西仍有延伸(A7區)，預測該區為隱伏巖漿巖體分布區。此外，A1～A6區也具有局部低重、高磁異常的組合特征，地表未見巖漿巖體或巖脈出露，將其解釋為隱伏巖漿巖體區。

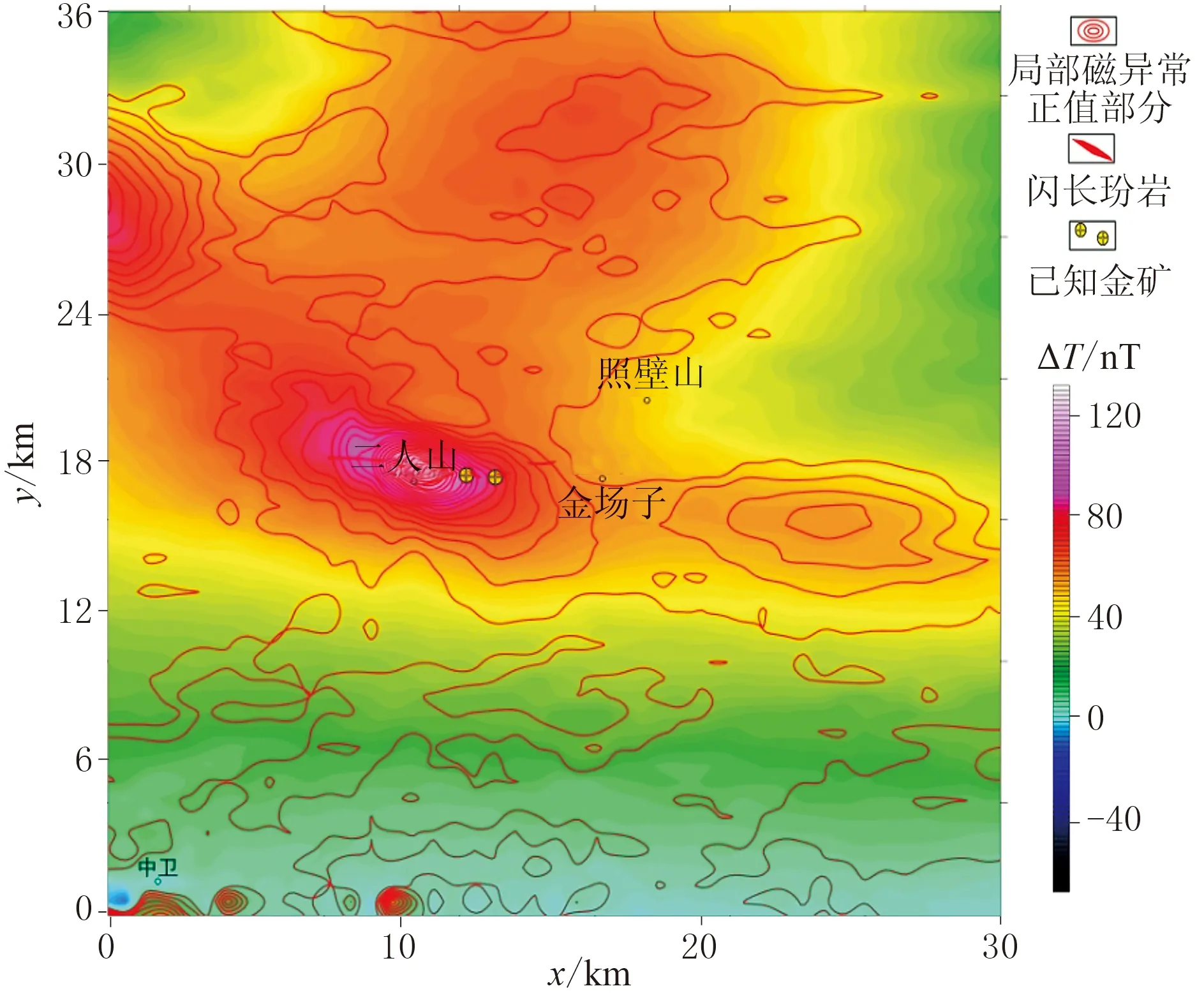
圖14 研究區化極磁異常疊加剩余磁異常圖

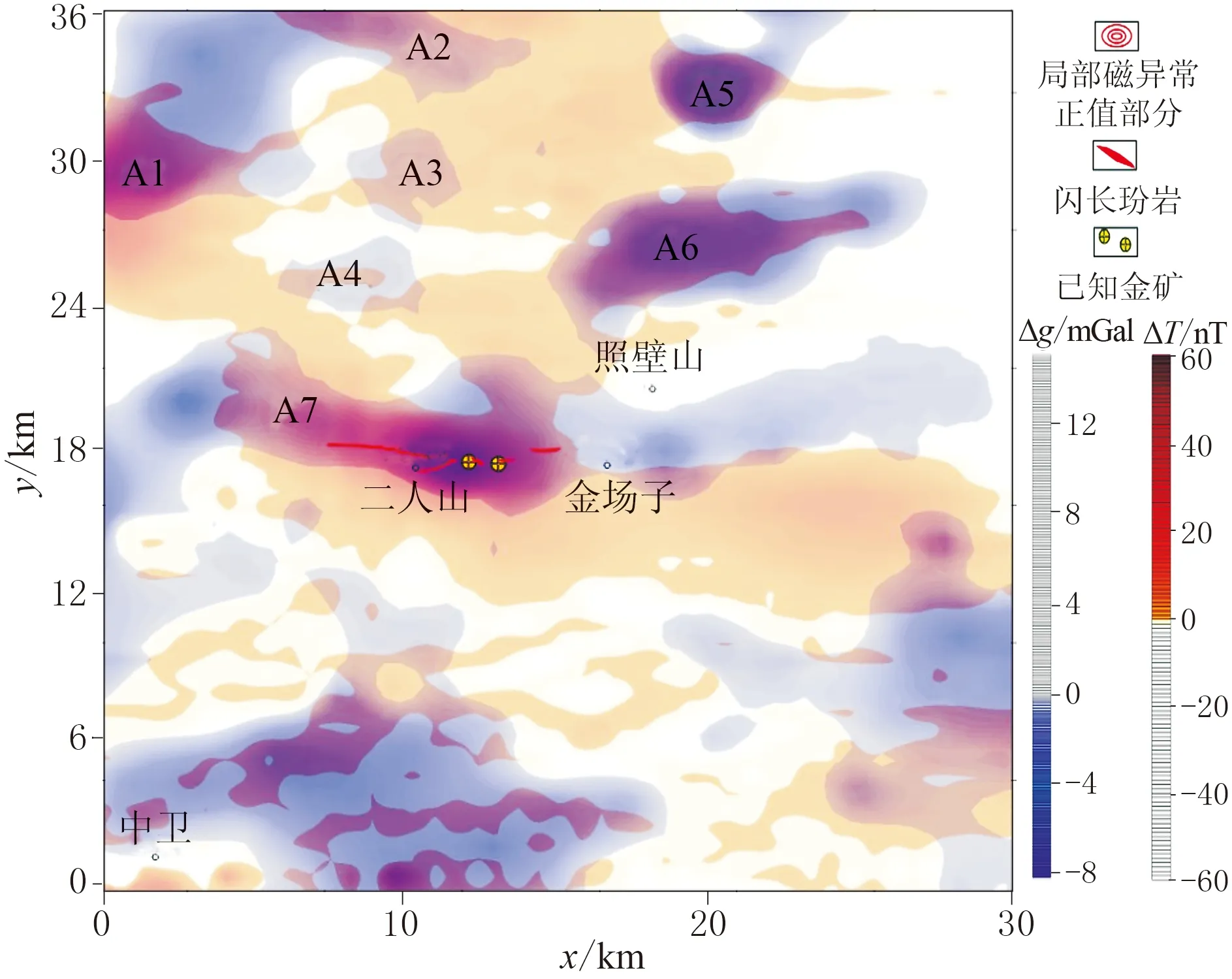
圖15 局部低重、高磁異常疊合圖及巖漿巖預測區域

7 結論和討論

本文主要研究魯棒主成分分析在位場分離中的應用。以模型數據為基礎，討論了位場信號的低秩性和稀疏性特征，從低秩性和稀疏性的角度論述了RPCA在位場分離問題中的地球物理意義，并結合理論模型提出適用于位場分離的參數選取方法。

區域場具有低秩性和局部場具有稀疏性是利用RPCA法實現位場區域場與局部場分離的基礎。從RPCA數學模型出發，該方法同時要求分離出來的區域場低秩且局部場稀疏，因此對分離出來的場具有更強的約束力，進而分離的結果更準確。由于核范數和(1,1)范數的共同約束，采用RPCA分離位場很容易達成一種相對穩態，而這一系列的相似分離結果對應位場分離的最佳結果。因此，與傳統位場分離方法相比，RPCA法的精度更高，并且在一定程度上更容易避免欠擬合或過擬合現象。同時對于稀疏且大幅值的噪聲，RPCA法能夠有效分離。

最后，將RPCA法用于寧夏衛寧北山地區的隱伏巖漿巖體預測，將分離得到的局部低重、高磁組合異常作為判斷巖漿巖發育區的標志，預測出7個火成巖發育區。

本方法的不足之處是需要對原數據進行變換得到延滯矩陣，即對一維數據Hankel矩陣化及求兩類優化問題最優解需要占用一定的內存，計算速度也沒有頻率域快。但是隨著工作站、并行機等硬件的普及算法的改進，這些問題最終可以得到解決。