基于二階磁張量歐拉反褶積的磁源單點定位方法

李青竹 李志寧 張英堂 范紅波

(陸軍工程大學車輛與電氣工程系，河北石家莊 050003)

0 引言

磁梯度張量(Magnetic gradient tensor，MGT)探測技術及其數據解釋與應用可視為磁法勘探領域的一項突破[1]。相較于磁總場強度和磁場矢量，磁梯度張量作為磁場矢量三正交方向上的空間變化率，對測量點的空間取向和旋轉噪聲不敏感，梯度測量與背景勻強場環境無關。磁梯度張量技術可提取關于目標體更豐富的姿態信息和磁源信息，分辨率高且抗干擾能力強，對復雜環境的適應性較強[2-3]。利用磁梯度張量數據可實現航磁探測、礦產勘探與土壤黑色金屬搜索、探尋未爆彈、排雷、潛艇偵查或水下金屬目標定位及反演識別等[4-6]，應用前景十分廣闊。

當觀測距離超過目標體尺度的2.5倍時，磁性目標可簡化為磁偶極子[7]。在實測過程中，對多點根據磁偶極子場源理論進行目標定位時，測量結果如果相對穩定，則表明此時目標體可以當做磁偶極子。Nara等[8]提出基于歐拉反褶積的磁偶極子單點定位算法，通過計算張量矩陣逆與磁場矢量的乘積來估算磁性目標的位置。然而，實際應用中很難對背景地磁場與目標體的磁異常場進行分離，因而對目標體的定位精度受到限制。若想在地磁背景場中有效提取磁異常場源信息，可利用不同測點的場數據構建線性方程組，求解位置矢量，即多點定位[9-10]，但是定位精度會受到航線選擇的限制，且對系統姿態及位置的精度要求很高。

為在單一測量點處實現磁異常目標體的精確定位，本文對磁偶極子張量場和矢量場均滿足的歐拉反褶積方程求導，進而構建一、二階張量矩陣與位置矢量的關系方程，消除背景磁場，利用張量衍生不變關系得到目標位置信息的限定方程；同時提出二階張量系統的概念以及測量方法，以此對磁性目標進行單點定位。由于差分測量二階張量數據對傳感器輸出誤差十分敏感，故需配套磁梯度張量系統校正技術以提升張量數據的解釋精度。目前已有較為成熟的校正方法，如李青竹等[11-12]提出的平面十字形磁梯度張量系統的兩步線性校正和基于橢球擬合的磁梯度張量系統集成校正方法、尹剛等[13]提出的磁梯度張量系統非線性校正方法等，均能較準確地估計系統誤差參數，使單點定位方法可實現較高的目標定位精度。

1 磁梯度張量要素與張量不變量

磁梯度張量為磁場分量在正交方向上的空間變化率，共有9個元素，其中無源靜態磁場中某點磁場矢量旋度和散度為零[14]，故張量矩陣對稱且無跡，可表示為

(1)

式中：Bx、By、Bz為磁場矢量的三軸分量；Bij(i,j=x,y,z)表示磁梯度張量分量，共5個獨立分量，一般由差分磁梯度張量系統測得，如由四個磁通門傳感器組成的平面十字形結構張量系統[11-13]。張量運算時不隨坐標系旋轉而改變的量，稱為張量不變量。一些基本不變量[15]如下

(2)

式中： tr(·)代表求矩陣的跡；det(·)表示求行列式的值；λ1、λ2和λ3為G的特征值，滿足特征方程λ3-I0λ2+I1λ-I2=0。

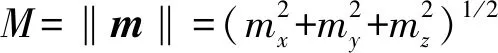
(3)

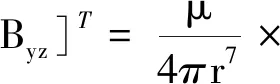
(4)

式中μ為介質磁導率， 在空氣中μ≈μ0，μ0=4π×10-7N·A-2為真空磁導率。

2 磁偶極子場張量衍生不變關系

2.1 特征值分析

特征值λ1、λ2、λ3及特征方程系數I0、I1、I2與場源磁偶極矩有關。若m、r已知，聯立式(2)和式(4)，可推導張量系統測量點處磁梯度張量矩陣的特征值

(5)

式中： |λ1|≥|λ3|、|λ2|≥|λ3|且λ2≥λ3≥λ1。令

(6)

根據G的對稱性與無跡性，可推導張量矩陣特征值λ1、λ2、λ3對應的特征向量

(7)

2.2 張量衍生不變關系

2.2.1 磁矩夾角不變關系

磁偶極子場源相對固定，當張量系統姿態變換時，同一測量點各姿態下不同的張量測量數據必然對應于恒定的磁矩矢量m和位置矢量r，因此m與r間的夾角θ0是不變的，將這個衍生不變關系稱為磁矩夾角不變關系，如圖1所示。假設該點處特征值λ1、λ2、λ3由實際張量系統測量并求解得到，則通過矢量的點積運算，聯立式(5)特征值解算式，可得到θ0的表達式

(8)

式中u為歸一化磁源強度(normalized source strength,NSS)。

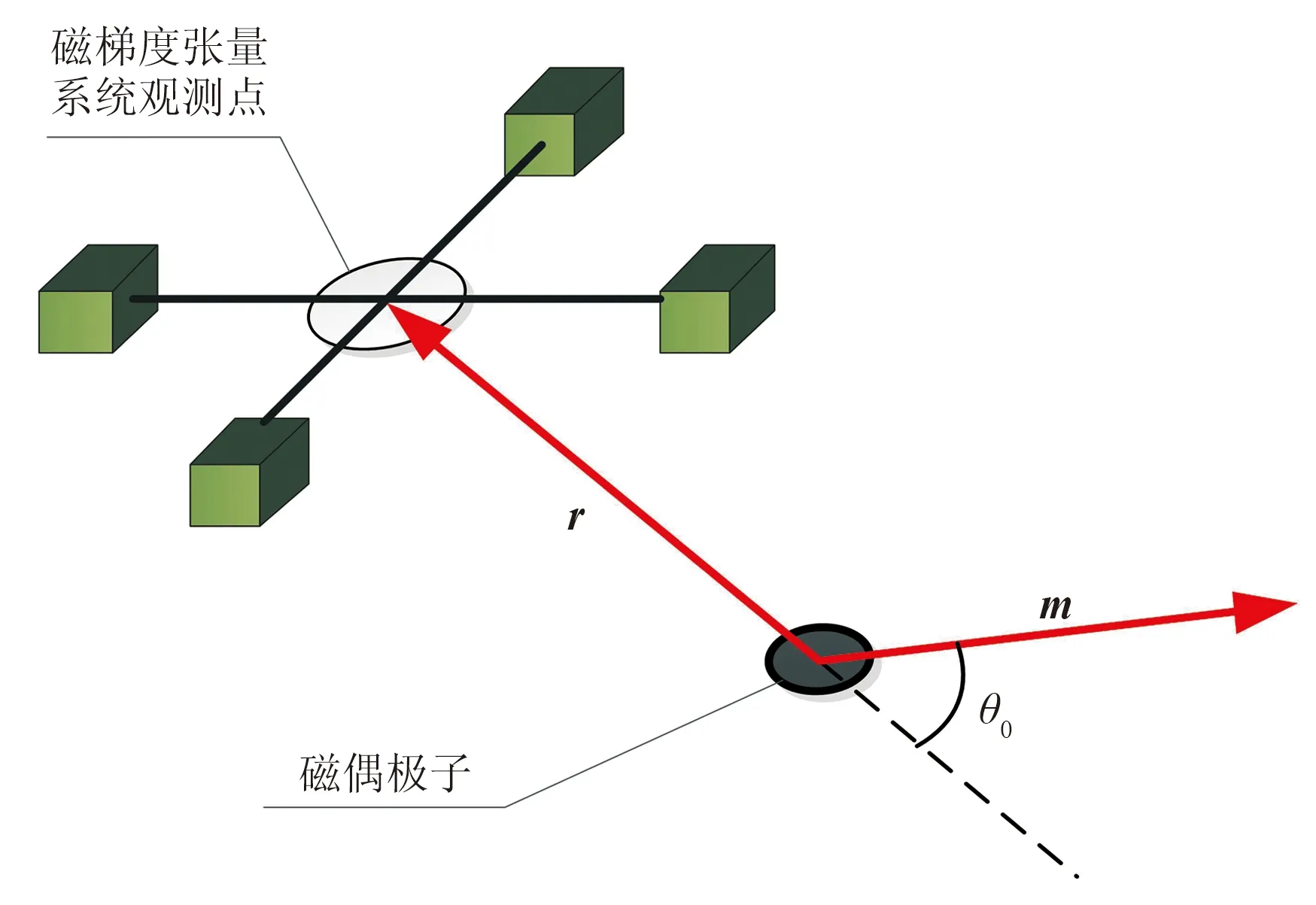
圖1 磁矩矢量與位置矢量夾角不變關系

2.2.2 特征向量空間不變關系

磁梯度張量系統空間姿態方向可以是任意的，選擇空間坐標系以磁偶極子為原點，r矢量方向為x軸正向，m與r的平面為坐標系xoy平面，則磁矩矢量與位置矢量的夾角不變關系可用如圖2所示的空間直角坐標系表示。

根據文獻[16]給出的偶極子位置表示方法，即磁矩矢量為m=(Mcosθ0,Msinθ0,0)T，位置矢量可表示為r=(r,0,0)T。聯立式(4)～式(8)，可推導出特征值λ1、λ2、λ3及其對應的特征向量v1、v2、v3

(9)

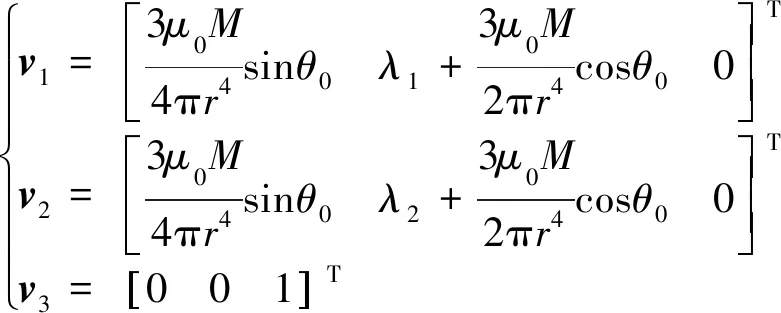
(10)

由式(10)可知，在建立的空間直角坐標系中，特征向量v3垂直于矢量m、r所在平面xoy，而特征向量v1、v2則與矢量m、r所在的平面xoy共面(圖2)。由于該空間坐標系沒有對磁偶極子的磁矩信息、張量系統測量姿態施加任何約束，而只與坐標系的選擇有關，因此可衍生為一般性結論：絕對值最小的特征值λ3對應的特征向量v3垂直于磁偶極子的磁矩矢量m和位置矢量r所在平面；最大和最小的兩個特征值λ1、λ2對應的特征向量v1、v2與磁偶極子的磁矩矢量m和位置矢量r所在平面共面。將上述兩個衍生不變關系稱為特征向量空間不變關系。

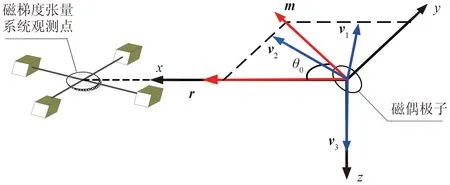
圖2 特征向量空間不變關系在直角坐標系中的表示

以上的張量衍生不變關系均與系統姿態無關，而僅與目標源磁矩矢量和位置矢量有關，故必然能為單點定位提供關于目標位置信息的限定條件。

3 二階張量歐拉反褶積定位方法

3.1 二階磁梯度張量矩陣與系統

磁梯度張量矩陣G各分量是磁矢量分量對于三軸坐標的一階偏導數，因此又稱為一階磁梯度張量。通過求解磁矢量在三軸方向上的二階偏導數，可得到二階磁梯度張量矩陣GII，共由27個元素組成

(11)

二階張量較一階張量可提取出更淺表的附加磁源信息，具有更強的磁源分辨能力。在無源靜態磁場中，GII的27個元素中僅有7個相互獨立，例如一組獨立元素為Bxxx、Bxyx、Bxzx、Byxy、Byyy、Byzy、Bzzz。以平面十字形磁梯度張量系統為原型，將其擴展為二階張量系統，能夠差分測量出磁矢量分量的二階偏導數。設計的該二階系統結構如圖3所示。

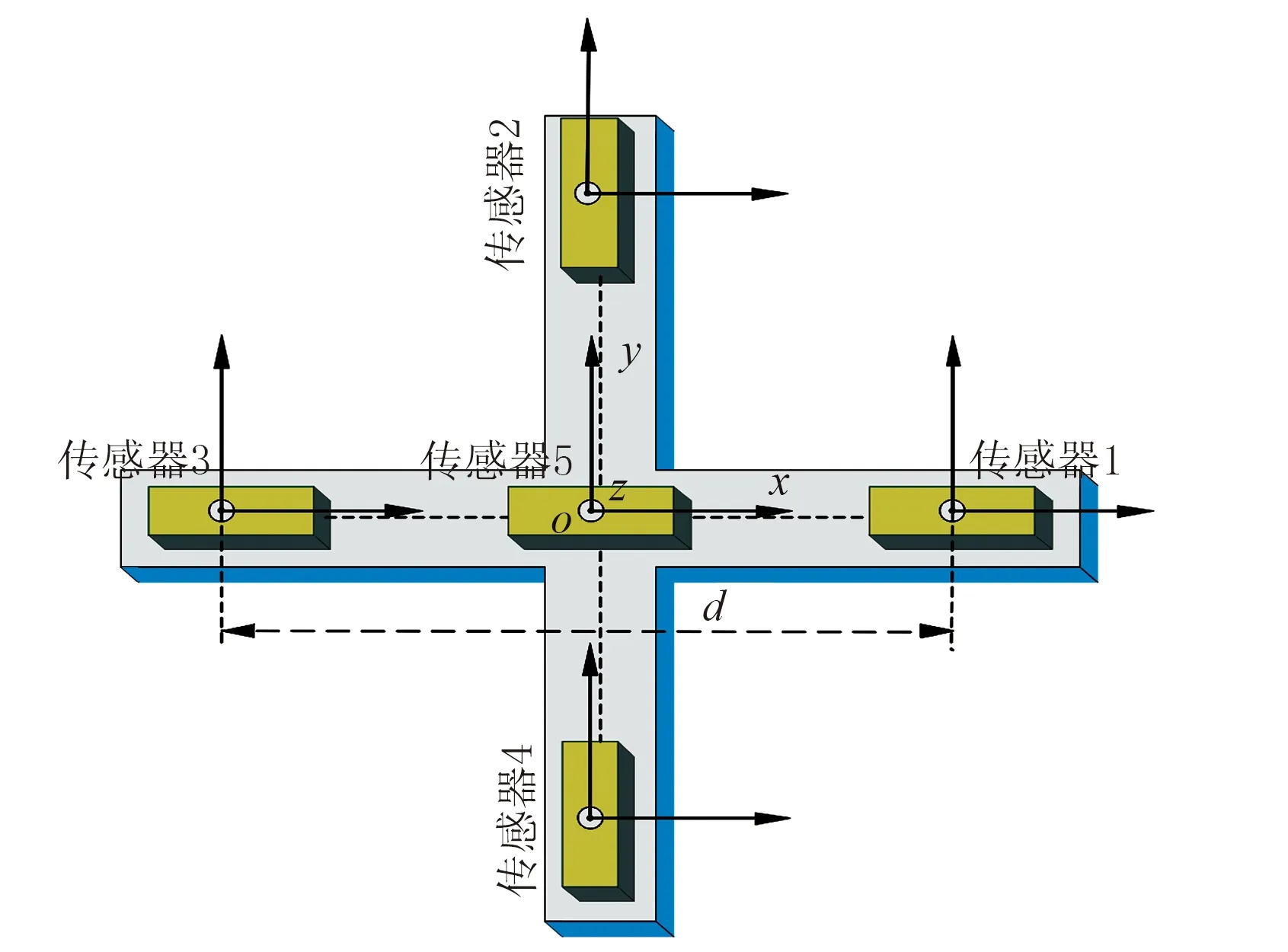
圖3 平面十字形二階磁梯度張量系統結構示意圖

由圖3可知，在原有平面十字形結構基礎上，在中心o點處添增加了一個傳感器5。該系統能夠測量得到二階張量矩陣27個元素中的6個和一階張量矩陣G

(12)

(13)

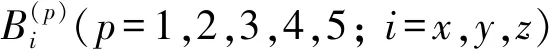
3.2 三維歐拉反褶積公式

利用歐拉反褶積法可以獲得場源位置信息。若n階齊次方程f(x,y,z)滿足[17]

(14)

該方程稱為歐拉方程。設地質異常體的坐標為(x0,y0,z0)，則在測量點(x,y,z)處的位場函數

(15)

=-Nf(x-x0,y-y0,z-z0)

(16)

當空間坐標系中磁異常場源中心位置坐標為(0,0,0)，則磁異常場源位置矢量r=(-x,-y,-z)T，該場源產生的磁場矢量三分量為

Bi(x,y,z)=f(x-0,y-0,z-0)

(17)

式(17)滿足式(16)的位場歐拉方程形式

(18)

式(18)可寫為矩陣形式

(19)

式(19)即為三維歐拉反褶積公式。Nara定位法[8]推導了磁偶極子梯度差，得到了式(19)中N=3的特例。當位場中僅存在磁異常場，對于給定待測場源的構造指數N，測得點(x,y,z)處張量矩陣的9個元素及磁場矢量的3個元素，就能反解出場源位置矢量r=(-x,-y,-z)T。然而，實際位場不會僅僅包括磁異常場。由于此處磁場矢量(Bx、Bx、Bz)僅由場源產生，而張量系統測得的磁場矢量為磁異常場與背景磁場的矢量疊加，故Nara法對實測數據的定位精度必然受到影響。

3.3 磁性目標位置的二階張量歐拉反褶積求解

為了從疊加場中有效分離出磁性體異常場，對式(18)中各等式兩邊分別對x、y、z求偏導

(20)

磁偶極子的構造指數為3， 用于磁性目標定位的式(20)可寫為矩陣乘積的形式

(21)

本文定義上式為二階張量歐拉反褶積公式，描述了磁偶極子在測量點處產生的一階、二階張量與其位置矢量之間的關系。基于3.1節中的二階張量系統可測得式(21)中二階張量矩陣的前6個元素和一階張量分量Bxx、Byy、Bzz。然而，位置矢量未知數為3， 則已知的兩個方程構成的線性方程組是欠定的。

由張量衍生不變關系可知，磁偶極子場源下張量矩陣G的絕對值最小特征值λ3對應的特征向量v3垂直于磁偶極子磁矩矢量m和位置矢量r所在平面，有

v3·r=[v3xv3yv3z][xyz]T=0

(22)

則式(22)可拓展為

(23)

式中Gv、gv均可通過二階張量系統測量后求解得到，據此可解得磁偶極子的位置矢量

(24)

再利用式(4)可解得磁矩矢量m。該方法僅需利用單一測量點的一階、二階張量數據便能實現磁偶極子的單點定位。

4 仿真分析

將磁偶極子置于真空空間(8m,5m,-4m)處，磁矩模為8000A·m-2，磁偶極子磁偏角為30°，磁傾角為40°。假設地磁背景場為勻強磁場，地磁總場強度(Total magnetic intensity，TMI)為55000nT，磁傾角為60°，磁偏角為-7°(西偏)。模擬搭建一個二階平面十字形磁梯度張量系統[11]進行測量，基線距離d設為0.4m。單航線測量從(-20m,0,0)到(40m,0,0)，測量試驗如圖4。

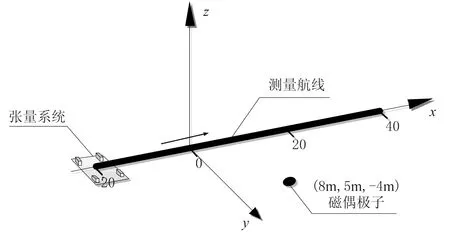
圖4 磁偶極子場源張量系統單航線測量試驗示意圖

航線運動過程保持系統姿態不變，采樣間隔為1m。在測量航線上各測量點處測得的磁場矢量三分量值如圖5所示。可見在龐大的地磁場背景下，由磁偶極子產生的部分磁場矢量分量場基本被淹沒，磁異常場難以有效分離。由文獻[11]知，磁傳感器實際輸出可表示為

(25)

式中：B1為傳感器實際輸出；ix、iy、iz為零位偏差；cx、cy、cz為靈敏度標度因子；φ、θ、ψ為非正交角；α、β、γ為非對準誤差角；w為測量噪聲；B2為理想輸出。利用圖3中的5個傳感器的位置仿真出該點處的航線測量數據，共三組作對比。

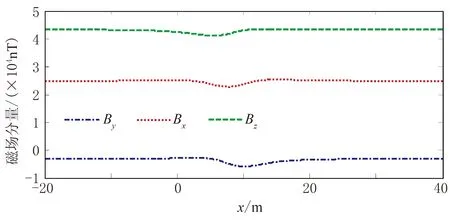
圖5 單航線測量中磁場分量

①理想組：誤差為零、測量噪聲為零；

②實際組：隨機預設各傳感器的12個誤差參數，并加入均值為0、方差為1nT的高斯噪聲，預設參數值列于表1中；

③校正組：使用兩步線性校正方法[11]對②中預設誤差后的各傳感器的12種誤差參數進行估計，并以此對實際組中的測量值進行校正。

由式(1)可知G為對稱矩陣，但式(13)中Bxy與Byx測量值存在差異，可視其為兩個獨立分量，此時G中共有6個獨立分量。利用本文方法對航線上所有測量點的①、②、③組測量數據分別計算磁偶極子位置坐標，則該測量航線三組測量數據下該二階張量系統測得的各測量點的一階張量的6個獨立分量、二階張量的6個獨立分量、估計得到的磁性目標空間位置圖、磁性目標位置的坐標分別如圖6、圖7和圖8所示。

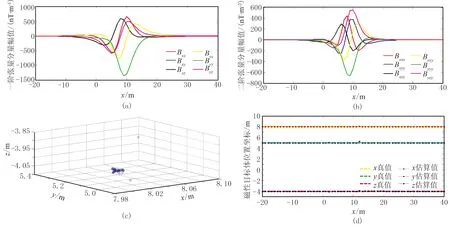
圖6 各傳感器不加誤差、噪聲時的單航線張量測量結果及目標定位結果

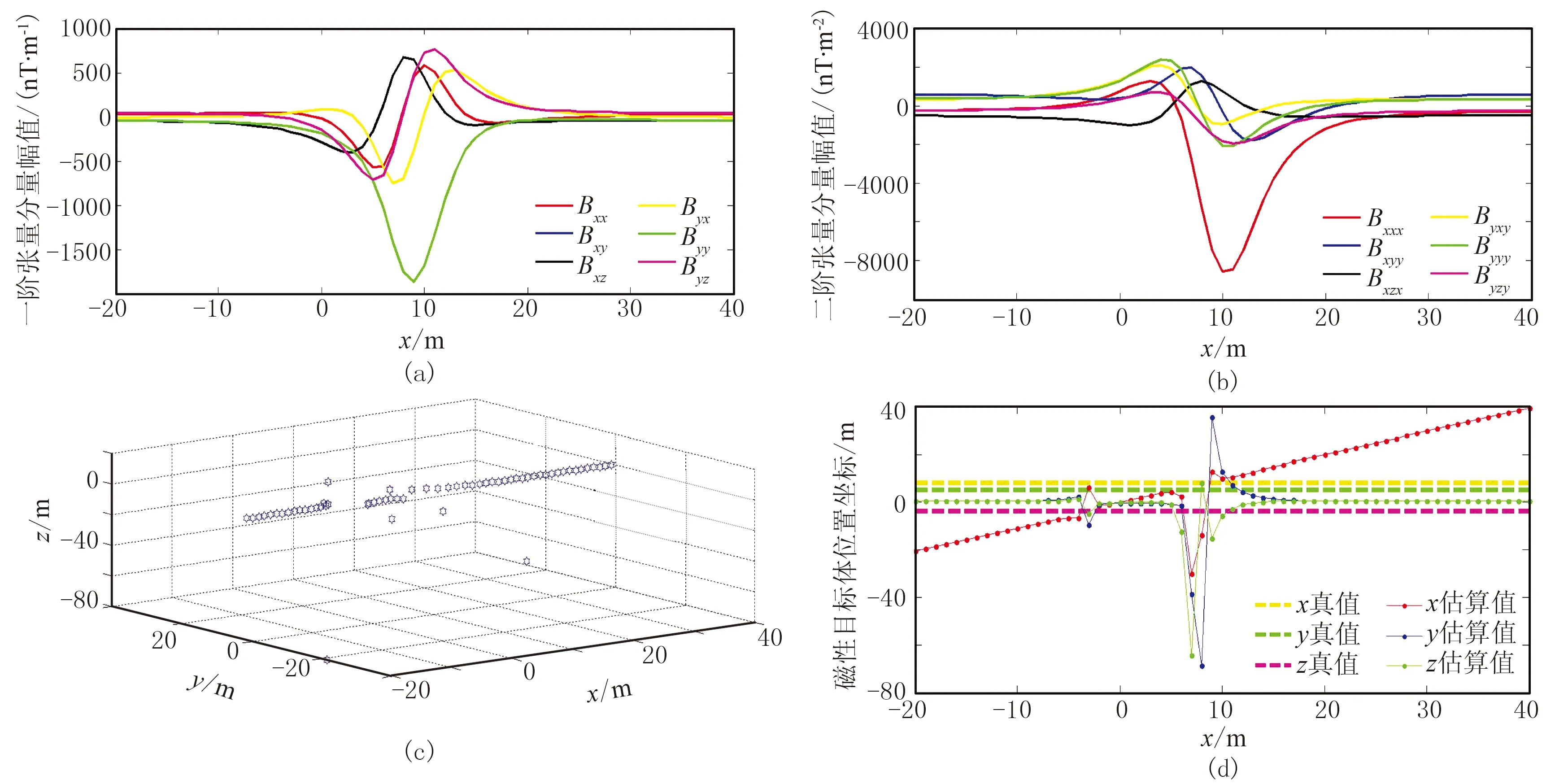
圖7 各傳感器加入誤差、測量噪聲時的單航線張量測量結果及目標定位結果

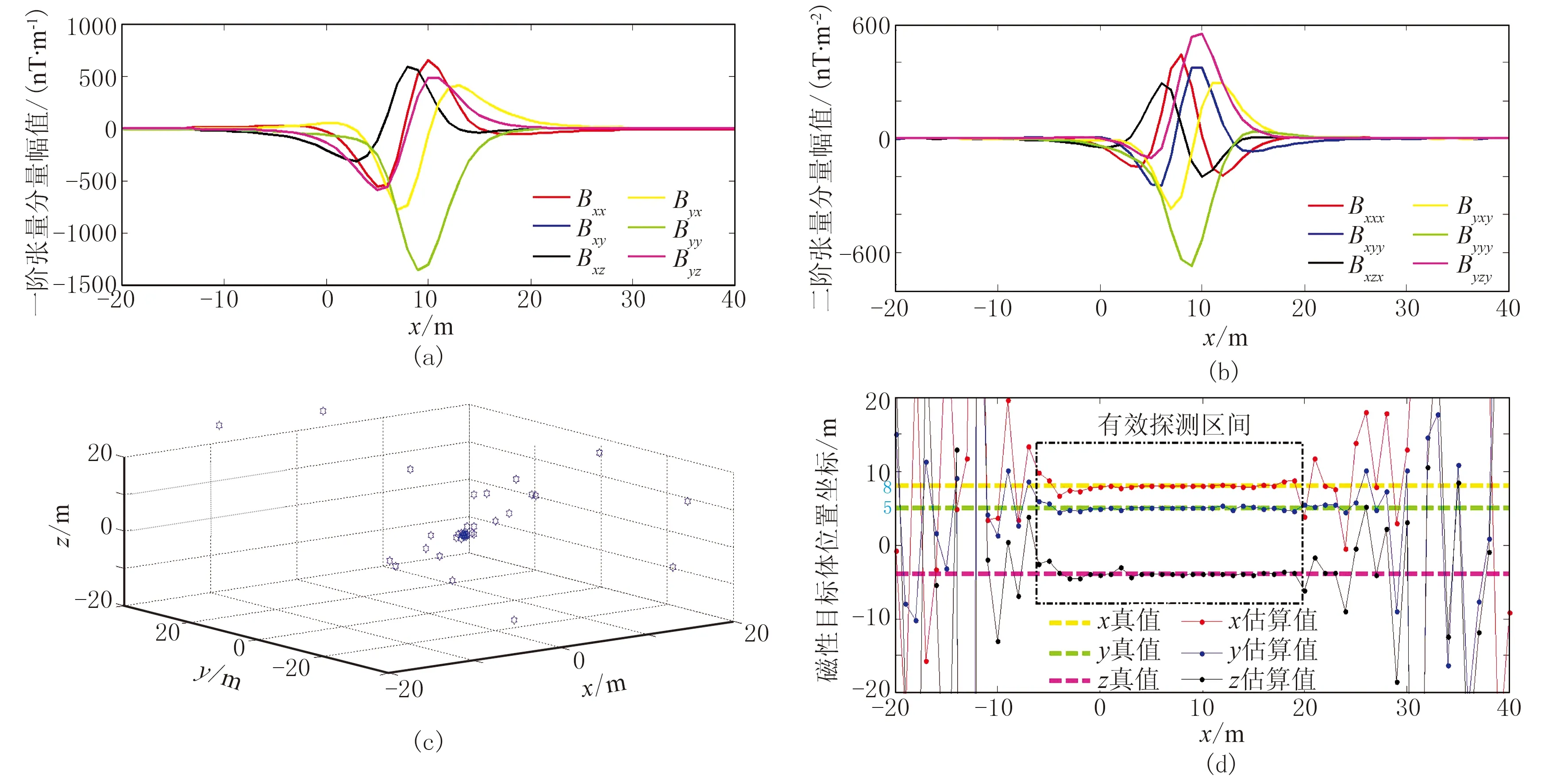
圖8 各傳感器進行兩步線性校正后的單航線張量測量結果及目標定位結果

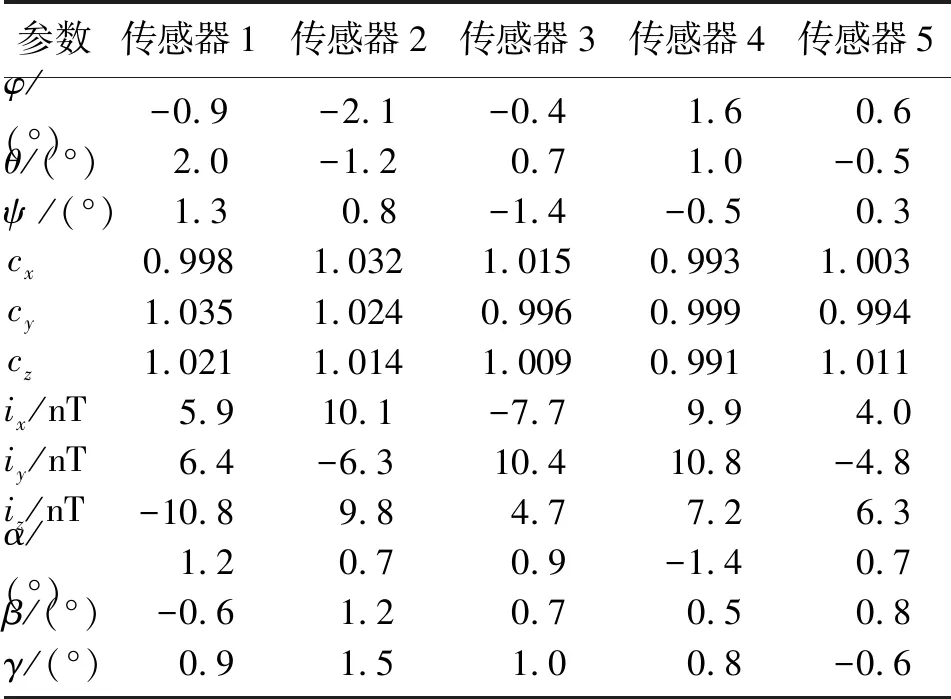
表1 預設5個傳感器系統誤差與非對準誤差

參考文獻[11]中的仿真結果，在相同測量工況的12個誤差參數的預設條件下，都引入了均值為0、方差為1nT的高斯噪聲，由第③步中估計的各個傳感器的誤差接近于0。由三組測量數據的定位結果可知： ①當未加入噪聲和誤差時，該方法對磁偶極子場源的位置估計誤差接近0，且在航線上所有點位均能實現有效探測并估計出準確的場源坐標；②各傳感器引入12個誤差和預設噪聲時，在該航線上無法有效探測到磁源目標；③加入均值為0、方差為1nT的高斯噪聲后，該二階張量系統在(-5m,0,0)～(20m,0,0)范圍內基本實現了有效探測及精確定位，超出該范圍的點無法被有效探測。

5 實驗驗證

為驗證方法對實際目標體的定位準確性及張量系統校正對定位精度的提升能力，設計如下實驗。

①搭建一個一階平面十字形磁梯度張量系統(圖9)，基線距離d為0.5m。二階張量系統在中心點o處增加傳感器5。為最大限度避免結構誤差，在單航線測量中可利用同軸其他傳感器對傳感器5讀數進行間接測量，從而獲得二階張量數據。間接測量示意圖見圖10。

②使用標量質子磁強計選擇地磁場穩定的某測區，面積為2.1m×2.1m。系統置于滑動臺架上，測量平面高0.65m。測得該測區內平均TMI標量為53911.48nT。盡管臺架盡量選擇無磁材質，但局部連接處仍存在磁干擾。為盡量避免磁干擾影響定位精度，利用橢球擬合集成補償方法[12]對測區內的張量系統進行校正參數估計，得到一組適用于該區域的系統各傳感器誤差補償參數(集成誤差補償系數F和集成零偏向量Iw)和對準參數(旋轉矩陣T)，見表2。該方法屬于間接校正法，不需要估計傳感器具體參數便可實現磁干擾環境下的磁梯度張量系統集成校正，對測量環境的硬、軟磁干擾具有良好的補償效果，同時可有效消除傳感器系統誤差和非對準誤差。磁傳感器輸出補償公式[12]為

圖9 平面十字形磁梯度張量系統示意圖

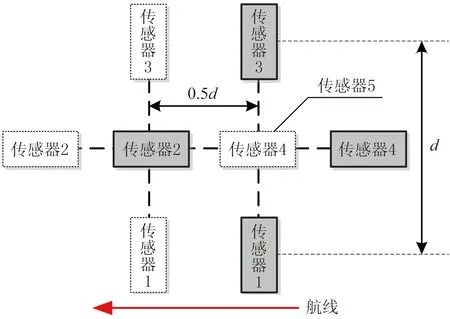
圖10 傳感器5的間接測量示意圖

Bc=TF(Br-Iw)

(26)

式中：Bc為理想傳感器輸出；Br為待補償的實際傳感器輸出。

③以測量平面xoy建立空間直角坐標系，x軸向東為正，z軸向上為正。以一小型磁鐵為探測目標，張量系統單航線測量方向自西向東，起始坐標為(0,0,0)，終點坐標為(2.1m,0,0)，目標磁鐵坐標為(1.10m,0.50m,-0.65m)，采樣間隔為0.05m，則該航線共有43個測量點，傳感器5的讀數間接等效于第6至第43測點的傳感器4讀數和第34至38測點的傳感器2讀數。該單航線測量實驗裝置示意圖見圖11。

由于探測距離遠大于磁鐵尺度的2.5倍，因此將其視為磁偶極子，并進行目標單點定位計算。首先，將步驟③中全部原始數據直接進行磁鐵位置坐標演算；然后利用表2中參數對步驟③中全部測量數據進行校正處理，再演算磁鐵坐標。校正前、后估計的磁鐵位置如圖12所示。將校正前、后估算坐標的精度使用均方根誤差(Root mean square error,RMSE)[19]進行量化

圖11 單航線磁性目標定位實驗裝置示意圖

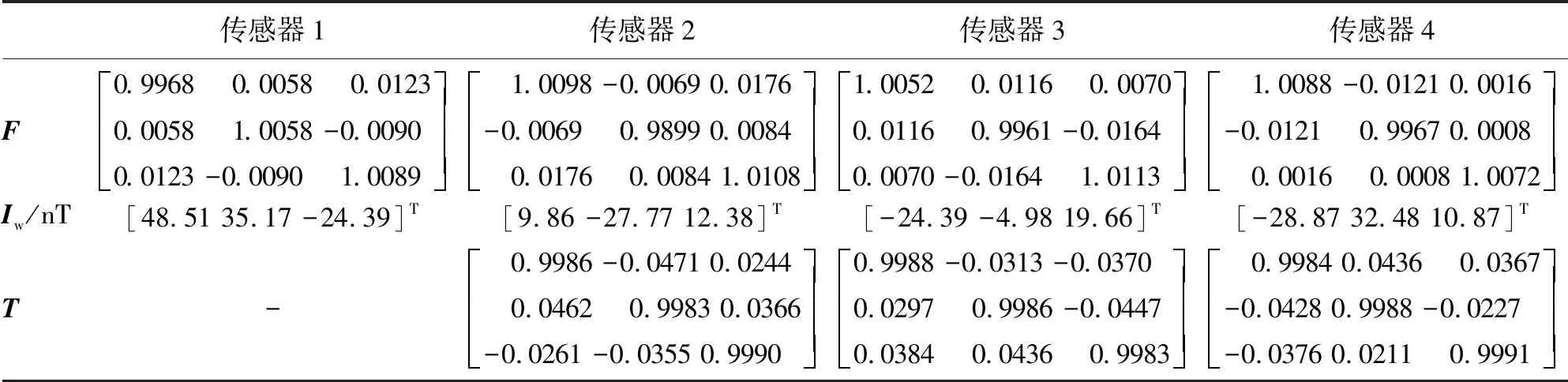
傳感器1傳感器2傳感器3傳感器4F0.9968 0.0058 0.01230.0058 1.0058 -0.00900.0123 -0.0090 1.0089é?êêêù?úúú 1.0098 -0.0069 0.0176-0.0069 0.9899 0.0084 0.0176 0.0084 1.0108é?êêêù?úúú1.0052 0.0116 0.00700.0116 0.9961 -0.01640.0070 -0.0164 1.0113é?êêêù?úúú 1.0088 -0.0121 0.0016-0.0121 0.9967 0.0008 0.0016 0.0008 1.0072é?êêêù?úúúIw/nT[48.51 35.17 -24.39]T[9.86 -27.77 12.38]T[-24.39 -4.98 19.66]T[-28.87 32.48 10.87]TT- 0.9986 -0.0471 0.0244 0.0462 0.9983 0.0366-0.0261 -0.0355 0.9990é?êêêù?úúú0.9988 -0.0313 -0.03700.0297 0.9986 -0.04470.0384 0.0436 0.9983é?êêêù?úúú 0.9984 0.0436 0.0367-0.0428 0.9988 -0.0227-0.0376 0.0211 0.9991é?êêêù?úúú

圖12 經橢球擬合集成校正前、后對磁鐵的定位結果

(27)

實驗結果表明，在該實驗工況下，校正后的系統對磁鐵坐標的估計精度可控制在均方根誤差10cm以內(表3)。當背景場更穩定、系統校正精度更高時，理論上能實現磁性目標厘米級別以上的精確定位。系統誤差校正技術的應用對提升張量數據解釋精度尤為關鍵。

表3 系統校正前、后磁鐵目標的坐標估計精度對比

6 結論

(1)推導的張量衍生不變關系表明：磁偶極子磁矩矢量與測量點的位置矢量夾角是恒定的，且僅與該點處張量矩陣特征值有關；磁偶極子場源的張量矩陣中間特征值對應的特征向量垂直于磁矩矢量與位置矢量，最大、最小特征值對應的特征向量與磁矩矢量和位置矢量共面。

(2)提出了平面十字形二階張量系統概念與測量方法，對三維歐拉反褶積公式求導后，利用一階、二階張量與張量衍生不變關系可求解磁源位置矢量。

(3)相比Nara定位法，本文方法能將磁異常信息與背景地磁場有效分離，坐標估計值唯一，在有效探測范圍內能實現測區中任意點對磁性目標的單點定位。

(4)仿真和實驗結果均表明：針對小尺度磁鐵的定位實驗中，在該實驗工況下，經誤差校正后的磁梯度張量系統的定位精度控制在均方根誤差10cm以內。

基于二階磁張量歐拉反褶積的磁源單點定位方法同樣適用于其他結構類型的二階磁梯度張量系統，且在實測中利用誤差校正技術極大地提升了磁性目標的定位精度，表明誤差校正對于提升張量數據解釋精度的重要性。高精度目標單點定位技術與張量系統誤差校正技術的結合，為后期針對磁異常體的反演識別、三維重塑等更深層次張量數據解釋提供了理論基礎與經驗參考。