Structural,elastic,and electronic properties of topological semimetal WC-type MX family by first-principles calculation?

Sami Ullah, Lei Wang(王磊), Jiangxu Li(李江旭), Ronghan Li(李榮漢), and Xing-Qiu Chen(陳星秋)

1Shenyang National Laboratory for Materials Science,Institute of Metal Research,Chinese Academy of Sciences,Shenyang 110016,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3School of Materials Science and Engineering,University of Science and Technology of China,Shenyang 110016,China

Keywords: topological semimetals,WC-type materials,MX family,elastic properties

1. Introduction

All types of topological materials-such as topological insulators[1-3]and topological semimetals[4-8]-have attracted the attention of researchers because their nontrivial topological phases and unique transport properties, which could establish a fertile ground for quantum computers and spintronic applications. The topological semimetals play a leading role to pinpoint numerous fermions phenomena in solid crystal systems. Moreover, due to its protection mechanism and diverse band crossing points in the electronic band structure near the Fermi level, the topological semimetals family can be classified into different groups, such as threedimensional Dirac semimetals,[9-25]Weyl semimetals,[26-48]Dirac nodal lines semimetals,[49-67]and semimetals with triply degenerate nodal points(TDNPs).[68-79,81]Furthermore,in the field of high energy physics, their realizations are also essential in solid crystals to establish a productive ground to study fundamental particles.

The non-centrosymmetric WC-type hexagonal structural MX family(MX =TaN,ZrTe,WC,MoP,TaS,TiS,TiSe,TiTe,ZrS,ZrSe,HfS,HfSe,and HfTe)compounds have raised extensive attention due to the incredible innovation of two coexisted phenomenon of fermions: (i)three-component fermions(TDNPs), and (ii) two-component Weyl fermions (WPs) in their bulk phases around the Fermi level.[70-75,78,79]The existence of triply degenerated nodal points (TDNPs) can differentiate the MX family from other renowned topological semimetal candidates. Meanwhile,the properties related with the electronic TDNPs and WPs have been already discussed in detail by using theoretical and experimental approaches in the literature.[68-79]Interestingly,we have recently found that several WC-type compounds commonly host the unique phononic triply degenerate nodal points (TDNPs) and phononic Weyl nodes(WPs)[79,80]in their phonon spectra.

Following these advances in topological electronic and phononic properties of these MX compounds, further interests have been motivated to see which of the other compounds are isoelectronic and isostructural WC-type systems. Therefore,we have further analyzed the MX compounds,which are the combination of group IVB elements (Ti, Zr, and Hf) and VIA elements(S,Se,and Te)of the periodic table. This family contains nine compounds, in which five compounds (TiS,ZrS, ZrSe0.9, ZrTe, and Hf0.92Se) have been experimentally reported by Harry and Steiger, Sodeck, Orlygsson, Schewe-Miller et al.[82-89]However, the remaining four compounds(TiSe, TiTe, HfS, and HfTe) have not been reported experimentally to date. Nowadays, because of the advances in experimental synthesis techniques-such as,chemical vapor deposition(CVD),physical vapor deposition(PVD),and molecular beam epitaxy (MBE)-it is possible to synthesize these materials. In this sense,here we have assumed that these four unknown compounds of TiSe,TiTe,HfS,and HfTe also crystallize in the same WC-type structure.

Within this context, through first-principles calculations,we have used the WC-type structure to explore systematically their structural stability, enthalpy of formation, elastic and electronic properties. The MX family has a simple WCtype structure(space group of P 6m2 and No. 187). We have investigated several detailed properties, such as structural parameters,enthalpies of formation,and elastic properties,such as bulk modulus B, shear modulus G, and Young’s modulus E. The Poisson’s ratio v, B/G ratio, electronic structure, and the effects of bond distance and unit cell volume on the elastic properties of the MX family were also evaluated. Interestingly, all of the compounds of the MX family have low enthalpies of formation and no negative frequency was noticed in the phonon dispersion. These results indicate their thermodynamically and dynamical stabilities,respectively.[79]These calculated results will provide basic structural,mechanical,and electronic properties for the MX family.

2. Computational methods

2.1. DFT calculations

In this work, all of the results of the density functional theory (DFT)[90,91]have been obtained by employing Vienna ab-initio simulation package (VASP) code[92-94]with the projector augmented wave(PAW)technique[95,96]through generalized gradient approximations (GGA) of the Perdew-Burke-Ernzerhof(PBE)exchange-correlation function.[97,98]The implemented PAW-PBE pseudo-potentials of all elements(i.e.,Ti,Zr,Hf,S,Se,and Te)are chosen by valence electrons states (i.e., 3p4s3d, 4s4p5s4d, 5p6s5d, and s2p4) and proper cutoff energy is selected according to their ENMAX parameters of elements in each compound. The Γ-centered grid is applied for significantly fasten energy converges for hexagonal structures with a proper set of k-points (21×21×21), and a very precise criterion of forces(below 0.0001 eV/?A)is used for structural optimizations.

2.2. Elastic constant calculations

In the literature,[99]the Voigt proposed a scheme for the determination of average elastic moduli of a single crystal to be established by assuming uniform strain throughout a lattice orientation of the crystal,and its values indicate the upper range of the actual moduli. Furthermore,in 1929,Reuss proposed another scheme to obtain the average elastic moduli of a single crystal by the assumption of uniform stress, and the values of resultant moduli indicate the lower frontier of the actual moduli of the crystals.[100]Both of these schemes are based on the assumption of uniform strain and stress in the crystal respectively and show the upper and lower limits of the actual elastic moduli but not the actual values of the elastic moduli of the crystal phase. To obtain the actual values of the elastic moduli (B&G) for a crystal phase, the R. Hill approximations[101]are used,and the resultant elastic moduli are equal to the arithmetic average value of the elastic moduli of the Voigt and Reuss schemes.[102]In addition,these elastic moduli were also used to determine the Poisson’s ratio ν and Young’s modulus E of the crystal phase.[103]

3. Structural and elastic properties of the MX family

3.1. Structural properties

The WC-type crystal structure of the MX family contains two atoms per unit cell,which is non-centrosymmetric without inversion center as shown in Fig. 1. The Wyckoff sites show the occupancy of atom X at the 1a Wyckoff site(0, 0, 0)and the M atom at the 1d Wyckoff site(1/3,2/3,1/2).

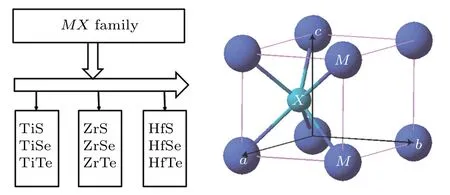
Fig.1. WC-type crystal structure of MX family(M=Ti,Zr,Hf;X=S,Se,Te).

We have optimized the lattice structures of nine MX compounds with the WC-type structure. Table 1 summarizes all of the optimized lattice constants as compared with the available experimental data. Our DFT calculated lattice constants for five experimentally known compounds(TiS,ZrS,ZrSe0.9,ZrTe, and Hf0.92Se) are in good agreement with the experimentally reported lattice constants with an error less than 1%.Furthermore, we have derived their enthalplies of formation(ΔH)at 0 K using the following equation:

where EDFT(MX) is the total DFT-derived ground-state energy of the stoichiometric MX compound and both EDFT(M)and EDFT(X) are the DFT-derived energies at their referred solid phases of M and X at their ground states, respectively. The structure optimization to their equilibrium states has been achieved at zero pressure for each elemental solid(Ti, Zr, Hf, S, Se, and Te) of the MX family to derive the ground-state energy.[104,105]The experimentally reported crystal structures such as Ti(hcp,P63/mmc,194),[106-108]Zr(hcp,P63/mmc, 194),[109-112]Hf (hcp, P63/mmc, 194),[113-115]S (orthorhombic, Pnm, 58),[116]Se (rhombohedral, R-3m,166),[117]and Te (hcp, P3121)[118,119]were used to calculate the ground state energy of each individual candidate. The results are further complied in Table 1 and these nine compounds have highly negative enthalpies of formation,indicating their thermodynamic stabilities. Furthermore,in our latest publication,[79]we have calculated the phonon spectra of these nine MX compounds, revealing no negative branches and noimaginary frequencies,which confirm their dynamical stabilities.

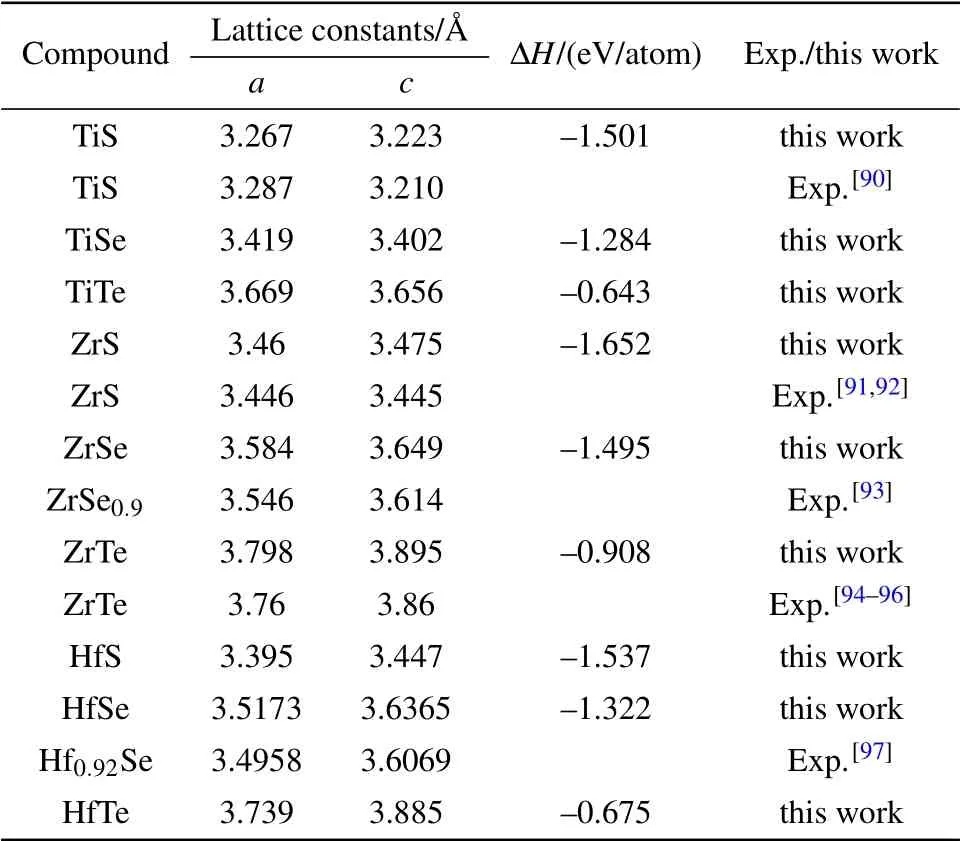
Table 1. DFT-derived lattice constants a and c and enthalpy of formation of single crystals,in comparison with available experimental data.

3.2. Elastic properties

The elastic constants are crucial because they allow us to investigate the stability of a crystal phase. They are also associated with numerous basic solid-state phenomenons such as,phonon dispersion,thermal properties,inter-atomic potentials,mechanical properties, and hardness.[120,121]Most recently,the elastic properties of WC-type topological semimetals of MoP, ZrTe, and TaN have been theoretically investigated by Guo et al.[122-124]To elucidate the elastic properties of these MX compounds in this work,we have first repeated the calculations of the elastic properties of ZrTe which is isostructural to the MX family, and the accomplished results were comparable with the previous work.[123]Theoretically,our proposed nine compounds of the MX family have a hexagonal structure phase and they require four-order tensors of 3×3×3×3 order matrix of 81 elements.[125]Due to the hexagonal symmetry of the MX compounds,the number of elastic constants Cijis reduced from 81 to 5, which are C11, C12, C13, C33,and C44.[103,123]For these nine compounds,the derived elastic constants are compiled in Table 2. In terms of these five independent elastic constants, we have found that all these MX compounds meet the mechanical criteria for hexagonal lattice,C44＞0,C11＞|C12|,and(C11+2C12)C33＞2C213.[102,126]Furthermore,according to the R.Hill approximation,we have derived the elastic moduli of the polycrystalline MX compounds in Table 2.

Table 2. The DFT-derived elastic constants Cij in GPa,C66=C11-C12/2,bulk modulus B in GPa,shear modulus G in GPa,Young’s modulus E in GPa,Poisson’s ratio v,B/G ratio,and hardness Hv in GPa at their equilibrium states.

From Fig.2,it can be seen that the bulk modulus B,shear modulus G, and Young’s modulus E follow the zigzag path from TiX to ZrX to HfX compounds. From MS to MSe to MTe, the data show a decreasing tendency against from Ti to Zr to Hf with increasing the atomic number of M. Among these compounds, the TiS compound has the highest bulk modulus (141.3 GPa), shear modulus (100.7 GPa), Young’s modulus (244.1 GPa) and the lowest Poisson ratio (0.21) as shown in Figs.2(a)and 2(b)respectively. The only exception is HfS, which has a bulk modulus of 153 GPa. Figure 2(c)illustrates the B/G ratio. According to the Pugh’s criteria[127]for the brittle or ductile mechanical properties of materials,eight compounds(TiS,TiSe,TiTe,ZrS,ZrSe,ZrTe,HfS,and HfSe) are in brittle because of their B/G values smaller than 1.75, whereas the compound HfTe is in the ductile manner.Because of the lowest Poisson’s ratio and B/G value, TiS would be the most brittle one among them. Furthermore, we have derived their theoretical Vickers’ hardness according to the proposed hardness model(Hv=2(k2G)0.585-3[128]using the inputs of both B and G.

Fig.2. DFT-derived(a)elastic moduli,(b)Poisson’s ratio,and(c)B/G.

4. Electronic properties of MX compounds

Furthermore,we have derived the total densities of states(DOSs)and the partial DOSs of the MX compounds in Fig.3,indicating that they share quite similar electronic structures.At first, they are typically metallic and their common feature is the existence of the pseudogaps at the Fermi level, mainly featured by the 3d, 4d, and 5d orbitals of the metallic components Ti, Zr, and Hf in the MX compounds. In Fig. 3, we have noticed obvious hybridization between 3d-Ti,4d-Zr,5d-Hf and 3p-S,4p-Se, 5p-Te in different energy ranges, but not at the Fermi level. In the total DOSs and partial DOSs of these compounds, the energy range decreases and shrinks towards the Fermi level due to the increasing atomic number of 3p-S,4p-Se,5p-Te with 3d-Ti,4d-Zr,5d-Hf,respectively. The presence of the pseudogap valley in the total TDOS at the Fermi level is a useful factor for the illustration of the electronic stabilities of these MX compounds.

Fig.3. The DFT-derived total densities of states and the partial density of states of MX (M=Ti,Zr,Hf;X =S,Se,Te). The Fermi level is set to the zero energy.

We have derived the electronic band structures of these nine MX compounds in Figs.4-6 with and without the spinorbital coupling (SOC). First, it can be seen that we have reproduced the electronic band structure of ZrTe, which is exactly consistent to that in Ref.[64],indicating that our current calculations are reliable. Second, the electronic structures of all these nine MX compounds look highly similar. When the SOC effect is ignored, two main features are observable (see panels (a)-(c) in Figs. 4-6). (i) Surrounding each K point in the bulk BZ, there is a Dirac nodal line (DNL) in the Kz=0 plane,as shown in Fig.7(a). These DNLs are clearly formed around the Fermi level due to the linear band crossing of their several inverted orbitals between the M dxz+ dyzorbitals and M dx2-y2+ dxyorbitals (M=Ti, Zr, Hf) surrounding each K point. (ii)A sixfold degenerate nodal point(sixfold DNP)locates at the position on the Γ-A direction around the Fermi level due to another type of band inversion between the doubly degenerate M dxz+ dyzand the M dz2-like orbitals at the A point of the bulk BZ (in Fig. 7(a)). Taking HfSe as an example, it can be clearly seen that without the SOC inclusion at the K point in the BZ the band inversion occurs between Hf dxz+dyzorbitals and Hf dx2-y2+dxyorbitals, resulting in the formation of the DNL surrounding the K point in the kz=0 plane(Fig.8(a)). At the A point in the BZ,the band inversion between the doubly degenerate Hf dxz+ dyzand dz2-like orbitals indicates the sixfold DNP occurring along the Γ-A line(Fig.8(a)).

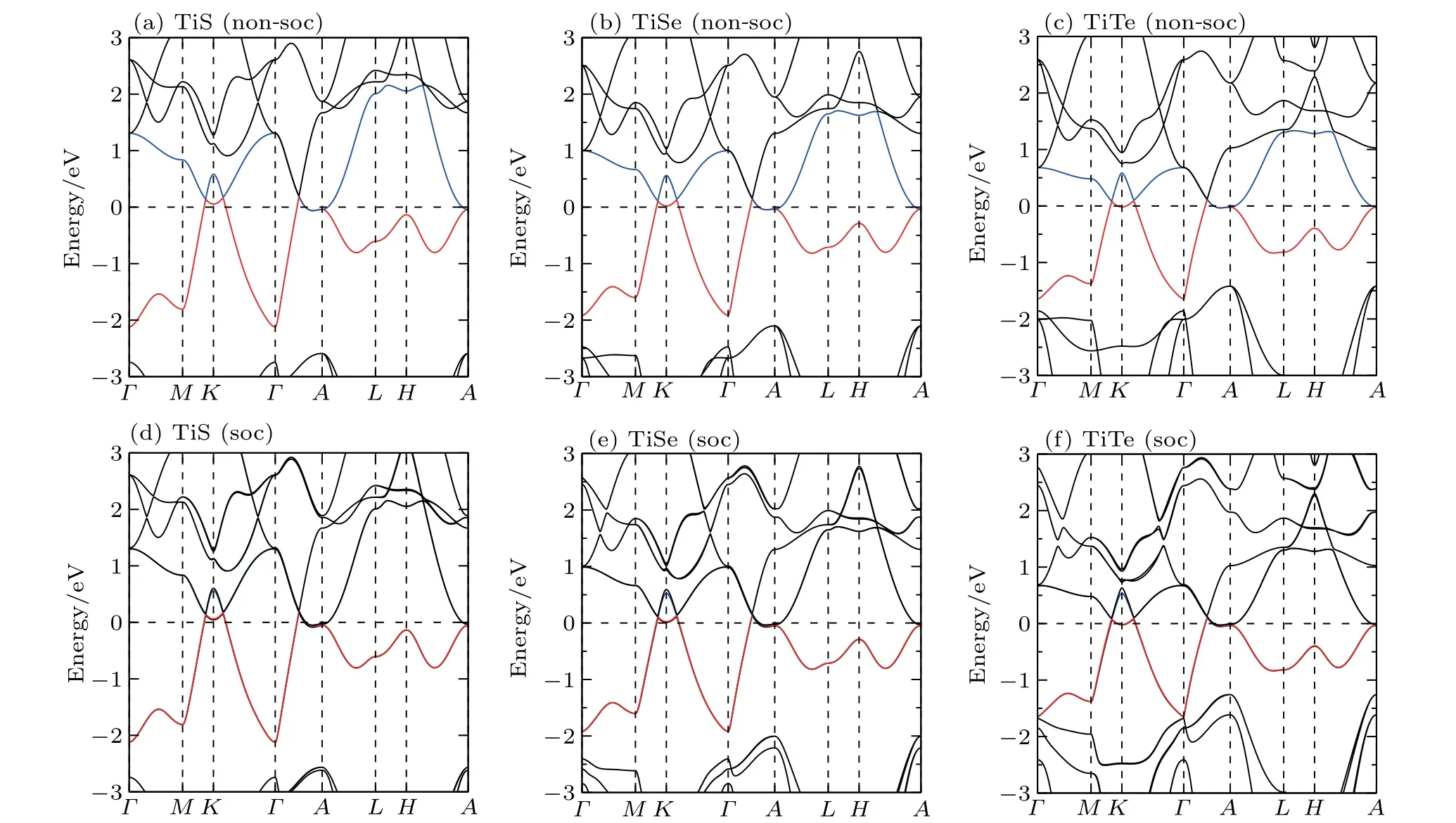
Fig.4. The DFT-derived electronic band structures of TiX (X =S,Se,Te): (a)-(c)without the SOC effect and(d)-(f)with the SOC effect. The Fermi level is set to the zero energy.

Because the masses of these elemental solids M and X are not very light, their SOC interactions should be considered. Once the SOC has been contained in their electronic band structures,we can see the highly apparent changes,particularly around the Fermi level. The only exception is the case TiS.Because TiS exhibits the weakest SOC effect among these nine compounds, as shown in Fig.4(a), the SOC inclusion does not obviously change its electronic band structure,indicating the coexisted six DNLs surrounding the K point and two sixfold DNPs along the Γ-A direction. Nevertheless,for other eight MX compounds, the SOC-induced modifications of the electronic band structures are relatively obvious. Because the MX lattice is lack of the inversion symmetry, each doubly-degenerate band in the case of SOC inclusion exhibits the so-called spin splitting. This results in two facts. First,each DNL around the K point in the kz=0 plane has to be broken into gap or WPs. After a careful search of the whole BZ, in our current cases for all MX compounds, each DNL is broken into a pair of WPs with opposite chirality, as illustrated in Fig.7(b). Therefore,in their BZ,there exist six pairs of WPs locating at the positions which are just slightly above and below the kz=0 plane. Second,the SOC inclusion splits each sixfold DNP into two TDNP [TDNP1 and TDNP2] as marked in Fig. 7(b) along the Γ-A direction. For instance,still for HfSe in Fig. 8(b), the SOC inclusion certainly splits the band around the Fermi level. This fact leads to two features:(i)the DNLs are split into the WPs at(0.27871,0.27871,±0.0100), as marked in Fig. 8(d). All these WPs have the same energy level of 33 meV above the Fermi level. (ii)Due to the SOC effect, the sixfold DNP along the Γ-A direction is split into two TDNPs, TDNP1(0, 0, 0.29081)and TDNP2(0,0,0.33169),as shown in the zoom-in plot of Fig.8(c). All these compounds indeed share the same behaviors. For ZrSe,a pair of WPs at (0.27314, 0.27314, ±0.01628) and TDNP1 at(0,0,0.2904)and TDNP2 at(0,0,0.3146)[79]and for ZrTe WPs at (0.2698, 0.2698, ±0.00655)[71]and TDNP1 at (0, 0,0.2834) and TDNP2 at (0, 0, 0.3313) appear. Of course, it should be emphasized that the appearances of TDNPs(TDNP1& TDNP2) are indeed protected by the C3zrotation and mirror symmetries,which are the same as those in both ZrTe and ZrSe cases.[71,79]

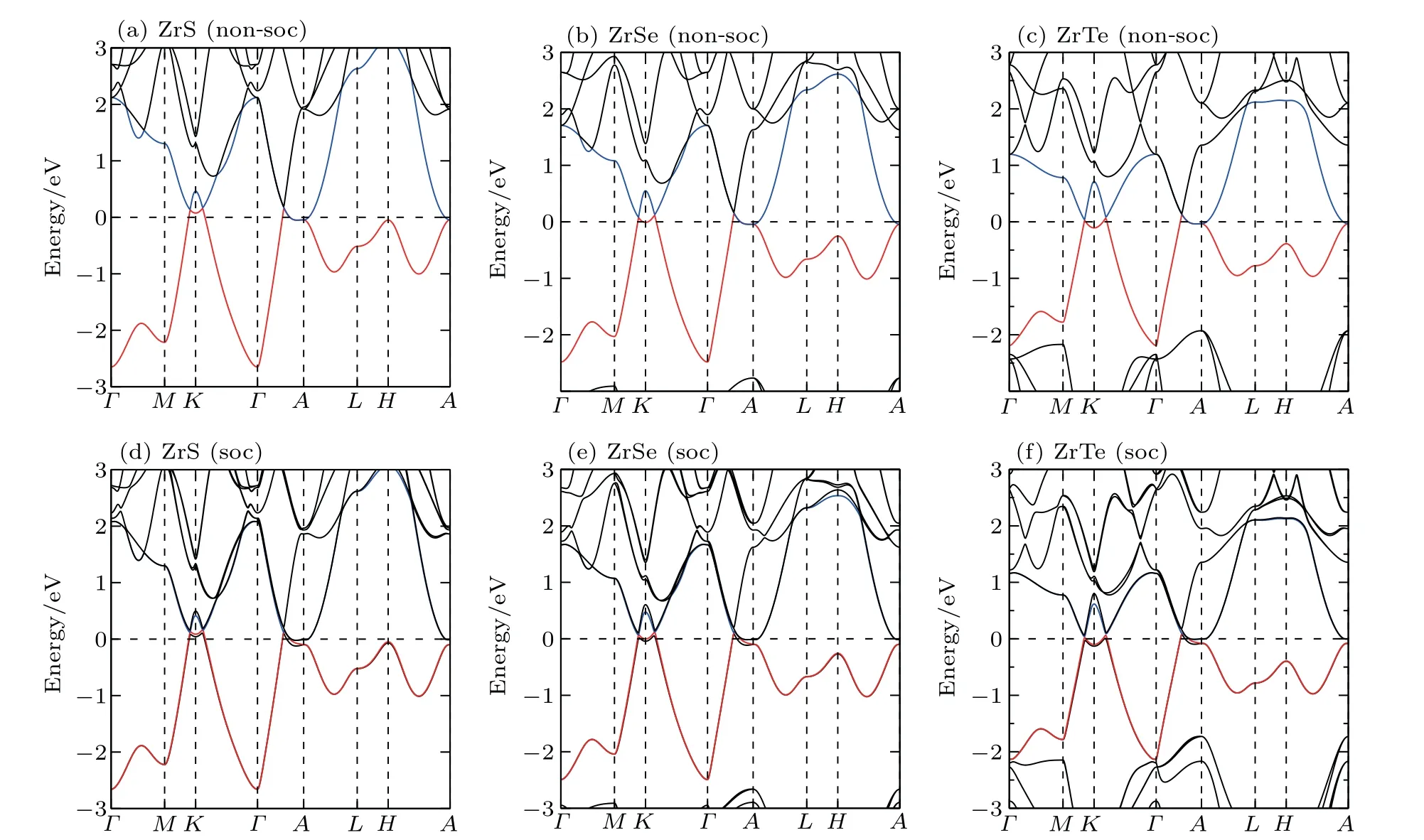
Fig.5. The DFT-derived electronic band structures of ZrX (X =S,Se,Te): (a)-(c)without the SOC effect and(d)-(f)with the SOC effect. The Fermi level is set to the zero energy.

Fig.6. The DFT-derived electronic band structures of HfX (X =S, Se, Te): (a)-(c)without the SOC effect and(d)-(f)with the SOC effect.The Fermi level is set to the zero energy.

Fig.7. Illustrations of BZ of MX. (a)Without the SOC inclusion,six DNLs surround the K point in the kz =0 plane and two sixfold degenerate nodal points (sixfold DNPs) locate at the Γ-A path of the BZ. (b) With the SOC inclusion, each DNL surrounding the k point will be broken into WPs with the opposite chirality, as marked by WP+and WP-. The sixfold DNPs will be broken into two TDNPs still on the Γ-A path.

Furthermore,as for ZrTe in Ref.[71],we can illustrate the topological property of the electronic structure using the Wilson loop method. Here,we have selected HfSe as a prototypical example to show the non-trivial topological feature of its electronic structure. We have first plot the DFT-derived electronic structure around one of the WPs for HfSe in Figs.9(a)-9(c)to illustrate the evolution of the electronic band structure around the WP.It can be seen that these WPs are clearly away from the kz=0 plane. Meanwhile, for HfSe it can be identified that all WPs have the same energy of 33 meV above the Fermi level. In addition,we also show the evolution of the socalled Wannier centers created along the kydirection in the two kz=0 and kz=π planes in Figs.9(d)and 9(e). Accordingly,the Z2numbers(namely,counting the times of Wannier center crosses a reference line)of both these planes are odd,signifying their topological non-trivial electronic feature. Of course,the other members including ZrTe in this family are similar to each other with the coexisted WPs and TDNPs in their bulk electronic structures. Of course, because of their non-trivial topological nature on some certain surface,there would exhibit some topologically protected surface states. These non-trivial surface states of both ZrTe and ZrSe have been discussed in details in Refs.[71]and[79],respectively.

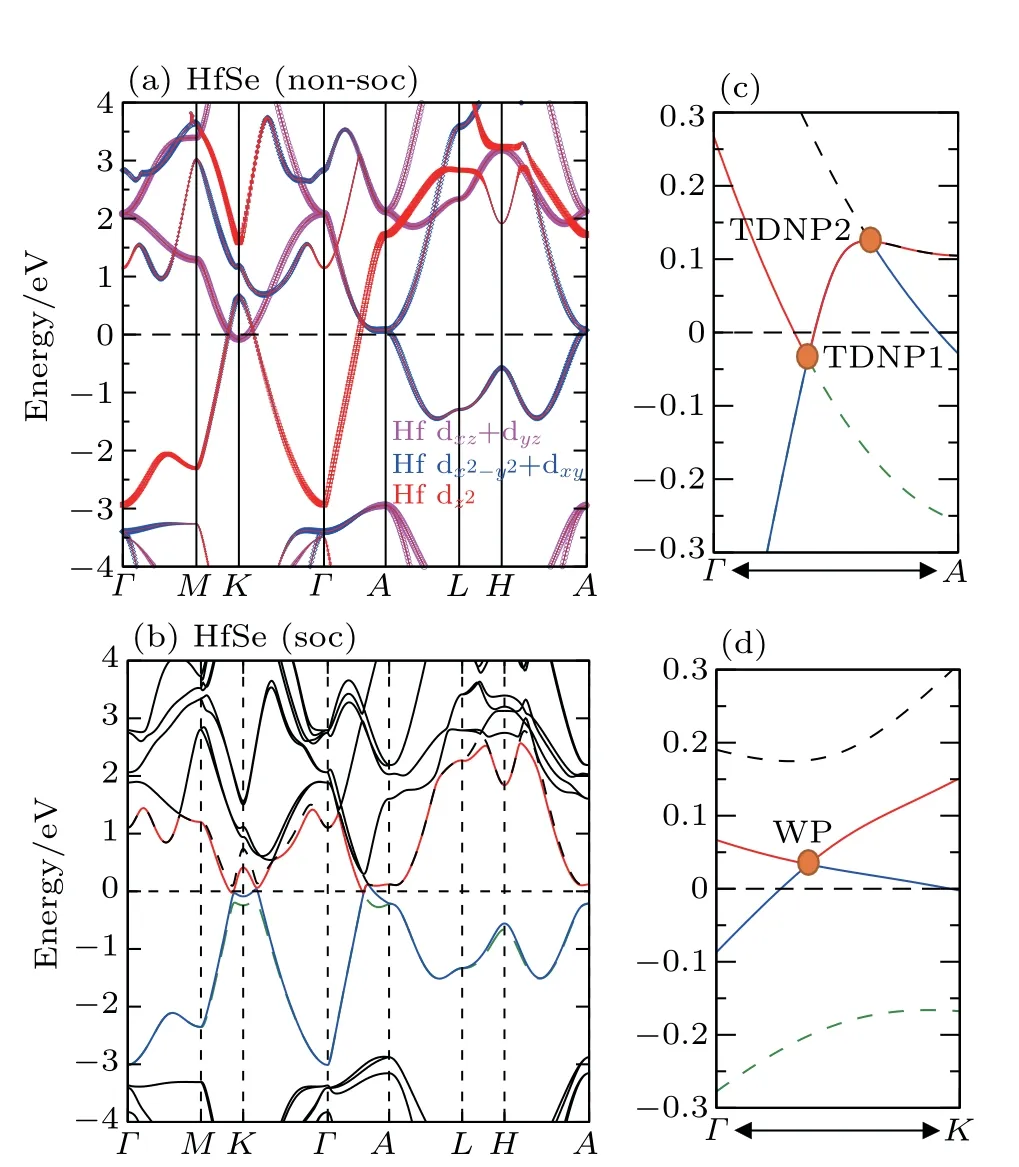
Fig. 8. Electronic structures of HfSe. (a) Band structure without the SOC inclusion shows the band inversion between dxz+dyz and dx2-y2+dxy at K and the band inversion between dz2 and dxz+dyz orbitals at the A point. (b) Band structure with the SOC inclusion. (c)The zoom-in visualization of TDNP1 and TDNP2 along the Γ-A direction in panel (b). (d) The zoom-in bands crossing one WP (0.27871,0.27871,±0.0100)around the Fermi level with the SOC inclusion.

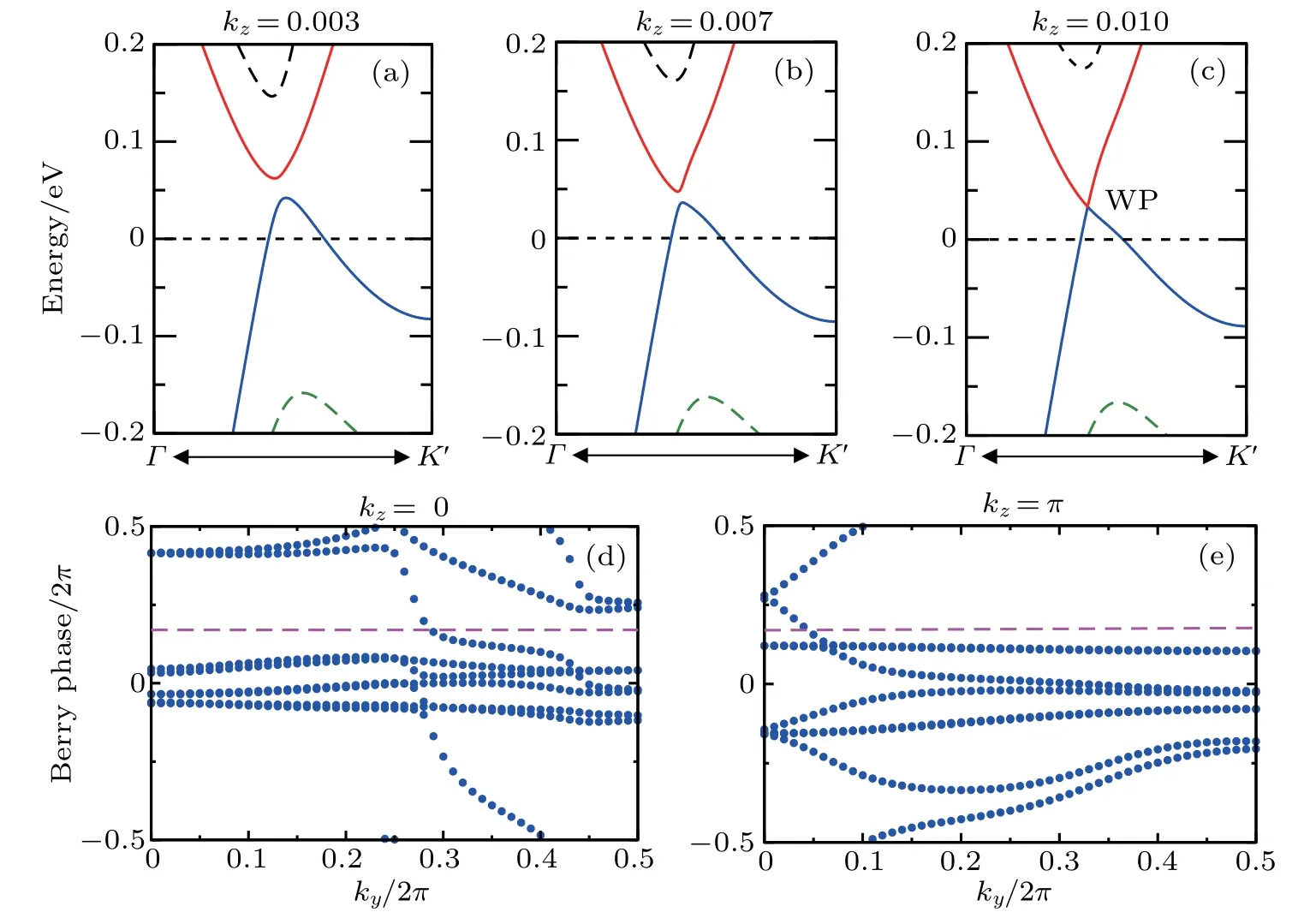
Fig.9. DFT-derived band structures around the WP node at(a)kz =0.003, (b)kz =0.007, and(c)kz =0.010(exactly corresponding to the WP node)for HfSe. The derived Wilson loops along the ky evaluation of the Berry phases of all occupied bands along the kx direction in both(d)kz=0 and(e)kz=π planes.

5. Conclusion

By employing the first-principles calculations, we have studied the structural, thermodynamic, elastic, and electronic properties of nine WC-type MX compounds(TiS,TiSe,TiTe,ZrS, ZrSe, ZrTe, HfS, HfSe, and HfTe). Five of them (TiS,ZrS,ZrSe0.9, ZrTe, and Hf0.92Se)have been theoretically derived to have comparable results with known experimental reported data. We have also predicted four new compounds of TiSe,TiTe,HfS,and HfTe which are thermodynamically and dynamically stable. All these compounds satisfy the mechanical criteria of hexagonal crystal phase, their bulk and shear moduli are obtained by R.Hill approximation. In addition,all these compounds have been theoretically proposed to be topological semimetals and revealed the analogous electronic band structures with the coexisted Weyl nodes and triply degenerate nodal points in their bulk phases like ZrTe compound,excluding TiS,due to the weak SOC effect.