電廠管道90°彎頭流動加速腐蝕的模擬研究

林 彤，周克毅，司曉東

(東南大學 能源與環境學院，南京 210096)

流動加速腐蝕(FAC)是在流動條件下，流體加速管道表面的氧化膜溶解在流動的水或濕蒸汽的過程，隨著管壁表面的氧化膜減薄，使金屬基體逐漸暴露于介質中，情況嚴重時會導致管道破裂，FAC是火電廠和核電廠管道最常見的失效原因[1]。近幾十年來，發生了多起由于FAC引發的管道泄漏事故[2-4]，造成嚴重的人員傷亡和巨大的經濟損失，嚴重威脅電廠的安全運行[5]。隨著我國超超臨界機組發展迅速，機組運行也逐漸暴露出一系列問題，如鍋爐壓差上升較快、結垢速率高、汽輪機高壓缸部位沉積嚴重等，根本原因是普遍存在FAC現象[6]。

FAC發生條件多為高溫、高壓、高流速，若要進行試驗需要大量的經費，采用計算機模擬耗時少、靈活性高、可重復性強。利用流體力學計算軟件，可以確定管道內部的流速、壓力分布，對于預測FAC發生部位有一定的意義[7]，并且FAC發生處多為彎頭、孔板和異徑管等流場變化劇烈的部位[8]。因此，筆者利用ANSYS軟件來研究電廠90°彎頭處FAC的規律，為類似問題提供指導。

1 FAC機理

由于邊界層的存在，電廠管道中的流體靠近氧化膜的流速較低、遠離邊界層的流速較高。主流中可溶性含鐵組分的濃度很低，邊界層中的含鐵組分會向主流方向遷移，使邊界層處含鐵組分減少，最終導致靠近邊界層的氧化膜以一定速率溶解。氧化膜內層結構致密，外層結構疏松，金屬基體生成的可溶性含鐵組分通過氧化膜的孔隙擴散到邊界層，造成含鐵組分從金屬基體向主流區的遷移，而主流區的高速流體不斷將含鐵組分帶走，造成碳鋼表面的持續腐蝕。FAC過程與靜止腐蝕相比，主要區別在于氧化膜-溶液界面上流體速度的影響，因此FAC可以分為傳質和電化學的耦合過程[9]。具體電化學反應過程見圖1[8]。

圖1 FAC機理圖

FAC是可溶性的含鐵組分由于濃度差的作用被主流帶走的過程。首先，在金屬氧化物界面上，金屬基體與H+發生反應生成Fe2+；其次，由于從金屬基體和主流區間的濃度差，一部分Fe2+運動到氧化膜附近。與氧化膜-溶液界面處Fe2+的濃度相比，水溶液中Fe2+的濃度非常低，在濃度差作用下，氧化物-溶液處的Fe2+向主區流擴散，此時流體不斷流動，帶走主流區Fe2+，擴散過程持續進行，導致壁厚持續變薄。FAC反應速率可表示為：

(1)

式中：KFAC為流動加速腐蝕速率，m/s；ceq為可溶性含鐵組分的溶解度，mol/L；c∞為主體溶液中可溶性含鐵組分的濃度，mol/L；K為反應速率常數，m/s；k為傳質系數，m/s；f為由金屬基體附近擴散到外部的溶解鐵的比例系數；δ為氧化膜厚度，m；n為氧化膜孔隙率；D為可溶性含鐵組分的擴散系數，m2/s。

Berge認為有大約一半含量的鐵直接擴散到主體溶液中[10]，即f=0.5。由于主體溶液中含鐵組分的濃度相較于含鐵組分的溶解度非常小，則可假定c∞=0，則方程變為：

(2)

2 計算模型

2.1 溶解度的計算

氧化膜內層結構致密，外層結構疏松，微溶于水。Fe3O4在高溫下與水溶液存在多個化學反應，反應生成物也各不相同。FUJIWARA K等[1]的研究表明溶液的溶氧量很低且其pH小于10時，Fe3+濃度非常低，所以氧化膜的溶解方程一般為：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

式中：K0、K1、K2、K3分別為式(3)、(5)、(7)、(9)的反應平衡常數。

磁性氧化鐵的溶解度為：

ceq=c[Fe2+]+c[Fe(OH)+]+

=c[H2]1/3(K010-2pH+K110-pH+

K2+K310pH)

(11)

溫度會影響化學反應速率，Ki均與溫度有關，其擬合公式為：

lnKi=[-Ai/T+Bi(lnT-1)+Di)]/R

(12)

式中：T為熱力學溫度，K；R是理想氣體常數，R=8.314 J/(mol·K)；Ai、Bi和Di為常數，其值見表1[11]。

表1 常數Ai、Bi和Di的值

2.2 傳質系數的計算

傳質系數受流場分布的影響，須得知90°彎頭的流場分布情況。遵循質量守恒、動量守恒和能量守恒，利用ANSYS軟件模擬得到彎頭內的速度分布，基于流體速度和傳質系數的關系求得傳質系數。模擬采用假設為：忽略重力的影響；流體介質不可壓縮；不考慮管子的散熱。

控制方程為：

(13)

(14)

(15)

式中：ρ為流體密度，kg/m3；u為流體速度，m/s；t為時間，s；μ為動力黏度，Pa·s；ui、uj分別為x、y軸方向上的速度分量，m/s；xi、xj分別為x、y軸方向上的坐標分量；Suj和ST分別為動量源項和能量源項；λ為熱導率，W/(m·K)；cp為比定壓熱容，J/(kg·K)。

傳質系數和流體速度之間存在如下關系[1,12]：

k=a(ρdu/μ)b(μ/D)c(D/d)

(16)

D=kBT/(6πμdM)

式中：a、b、c為常數；d為管道當量直徑，m；D為分子擴散系數，m2/s；kB為玻爾茲曼常數；dM為溶液中的離子半徑，m。

3 結果與分析

3.1 溶解度的計算結果

在調查的所有火電廠中，其中有60%的火電廠都在給水加熱器疏水系統發生過FAC[8]。以疏水部位的壓力和溫度作為參考，結合FAC高發的溫度區間范圍，將流體的溫度、壓力設定為150 ℃、2 MPa；電廠水側管道流速普遍在2～6 m/s，流體流速設定為3 m/s；pH隨著溫度改變，常溫(25 ℃)時pH為9.40，150 ℃時pH為6.86[13]。Berge等通過測量得出H2濃度在7.8×10-4～3.25×10-3mol/L，H2濃度取1.5×10-3mol/L[14]；根據T=423.15 K計算得到反應平衡常數K0、K1、K2、K3(見表1)；最終計算得到可溶性含鐵組分的濃度為6.477×10-8mol/L。

3.2 流場模擬結果

筆者建立的90°彎頭的三維數值計算模型見圖2。

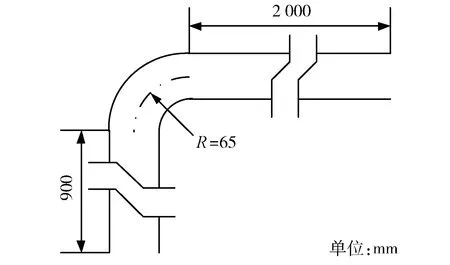
圖2 90°彎頭的三維數值計算模型

為了保證實驗段流體流動達到充分發展的狀態，同時實驗段出口流體流動不對實驗段造成影響，實驗段入口長度取為2 000 mm，出口長度取為900 mm。繪制幾何模型并將模型導入ICEM控件，利用O形網格剖分對90°彎頭進行劃分，構建結構網格，并且對模型的邊界層進行加密處理，共構建694 783個網格，對結構網格進行質量檢驗，得到網格質量在0.65～1.00，符合計算要求。將劃分好的網格導入FLUENT軟件，采用Pressure-Based求解器，使用Realizablek-ε模型，選用SIMPLE壓強-速度關聯算法，采用二階迎風差分格式，保持松弛因子默認設置，對建立的模型進行了數值計算。管內工質流速設定為3 m/s，管內直徑設定為50 mm，實驗段入口邊界條件為速度入口，實驗段出口邊界條件設置為壓力邊界(2.026 5×106Pa)，工作流體為液態水，密度為917.87 kg/m3，黏度為1.83×10-4Pa·s，特性為不可壓縮流體。湍流強度的設置參照下式[15]：

(17)

式中：I為湍流強度；Re為雷諾數。

經過計算可得I為2.948%。

筆者將90°彎頭模型進行了區域劃分，沿流動方向共分為9個區域，每隔10°進行劃分，由于管道軸對稱，沿管道徑向方向則劃分為0°、42°、138°、180°，φ=0°為內彎側，φ=180°為外彎側，具體見圖3。

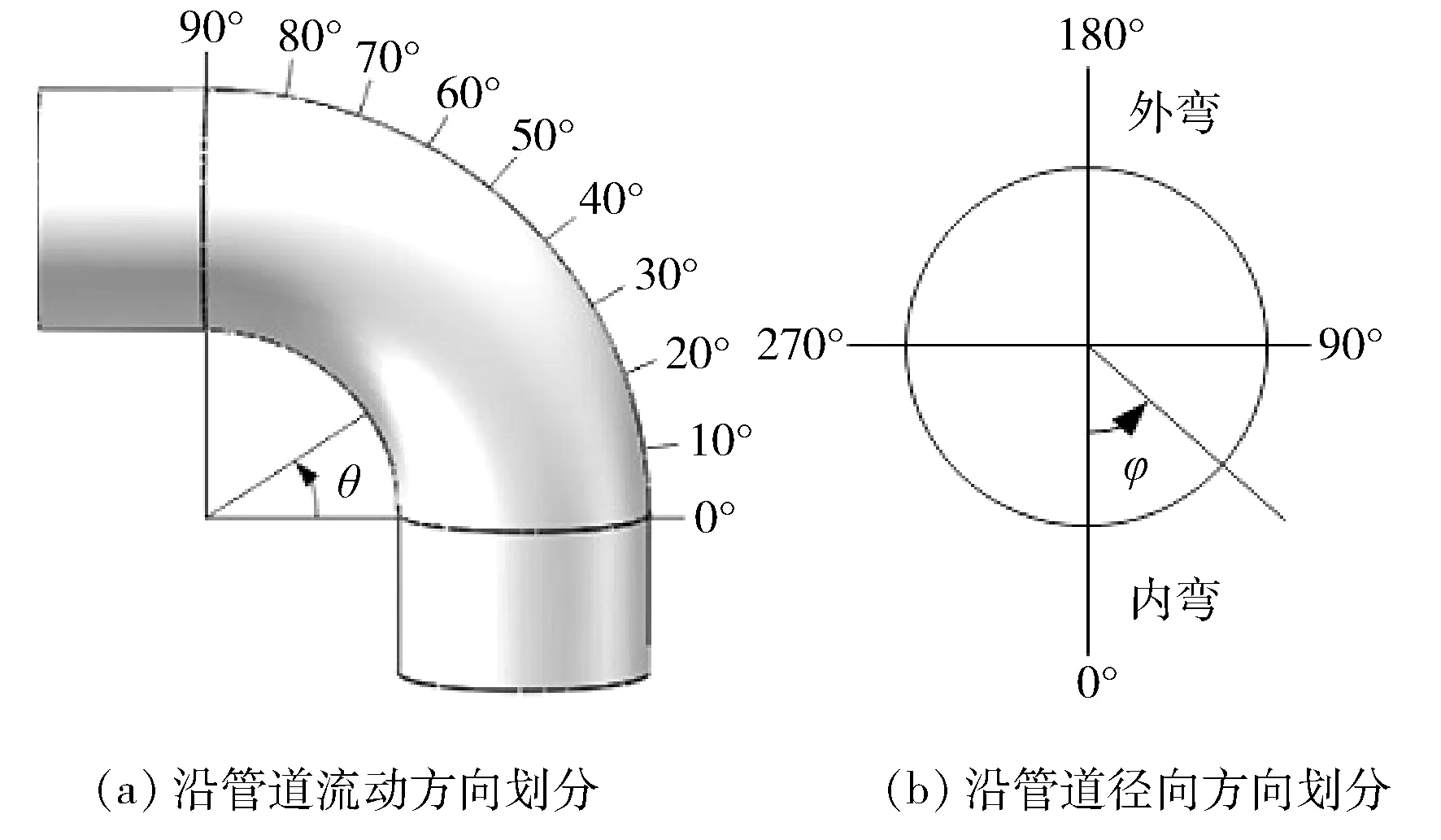
圖3 90°彎頭模型的區域劃分

圖4分別給出了流體速度為3 m/s，θ=0°、20°、50°、70°、90°時管道截面的流場分布。在彎頭內彎側流體速度沿流動方向逐漸增大，隨后不斷減小，在外彎側流體速度沿流動方向逐漸增大，直至與主流匯合。主流區域由于慣性的影響保持向前流動的趨勢，由于彎頭的阻礙不得不偏轉方向流動，主流區整體偏移，離開彎頭后流場逐漸趨于穩定。

圖4 不同θ下的圓管界面流速分布

在10個圓截面上各取4個點，分別為φ=0°、42°、138°、180°，流體速度分布見圖5，彎管內最大速度和最小速度都在內彎側，分別為3.8 m/s和0.505 m/s。內彎側流體速度從彎管入口處開始逐漸增大，到θ=20°左右達到峰值，然而內彎側由于發生二次流產生漩渦，消耗內彎側流體的能量，使得內彎側速度迅速下降。在φ=42°處，流體剛進入彎管，速度逐漸增大，隨著漩渦的出現，速度有下降趨勢，主流區從內側向外側偏移的過程中，經過φ=42°處，使得速度重新增大，當主流區已偏移到彎頭外側時，漩渦作用使速度繼續減小。彎管內其他部位由于距離漩渦較遠，受到影響較小，速度基本不變。流體繼續在彎管內流動，主流區向外側偏移，使得外彎側及靠近外彎側的速度逐漸增大到彎管出口均達到最大值。

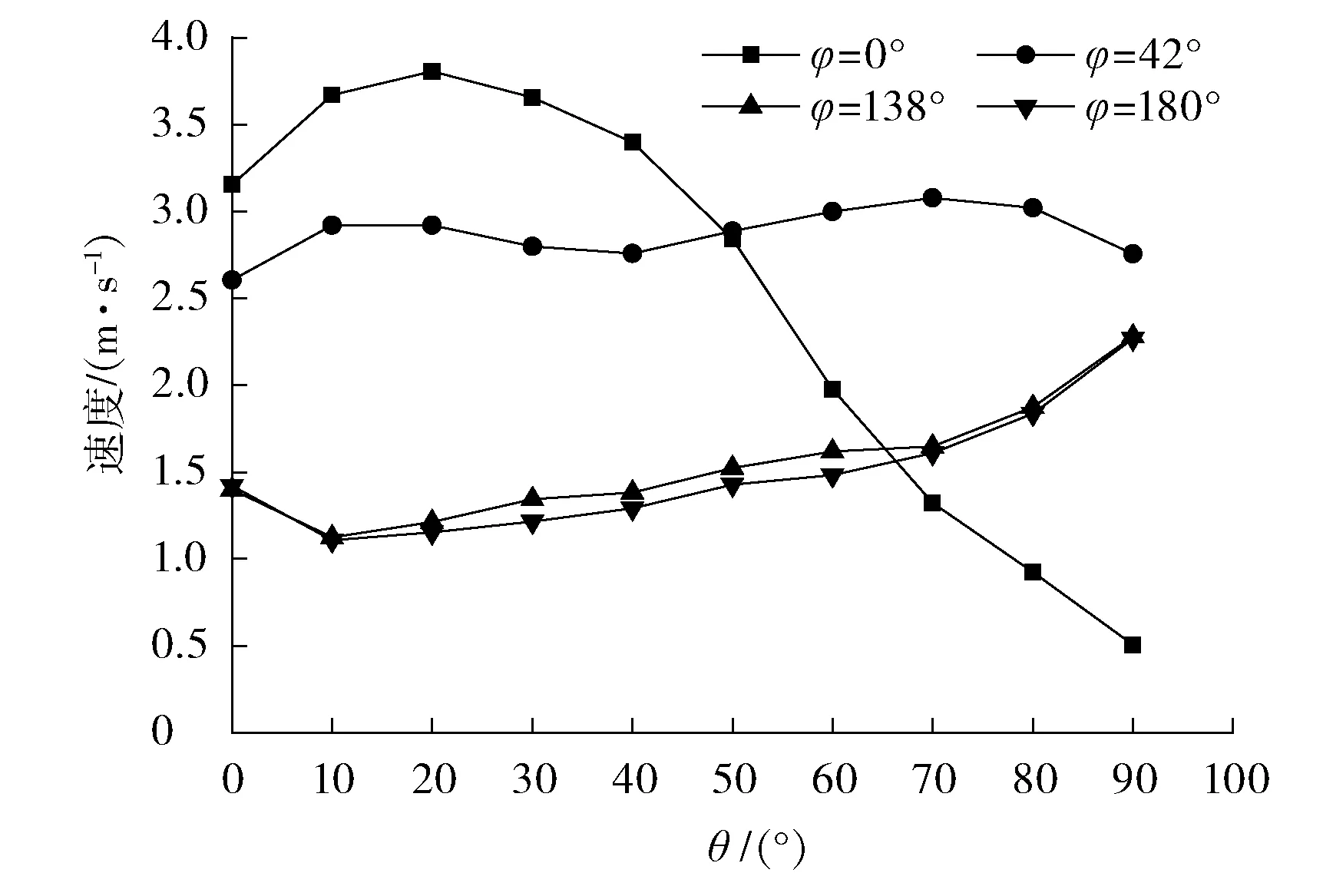
圖5 90°彎頭內各點的速度

3.3 傳質系數的計算結果

圖6為90°彎頭內各點的傳質系數。隨著流體速度的增加，使流場內的湍流強度增大，流體間的運動增強，使得動量輸送和熱傳遞變得頻繁，傳質過程增強，從而使傳質系數增大。

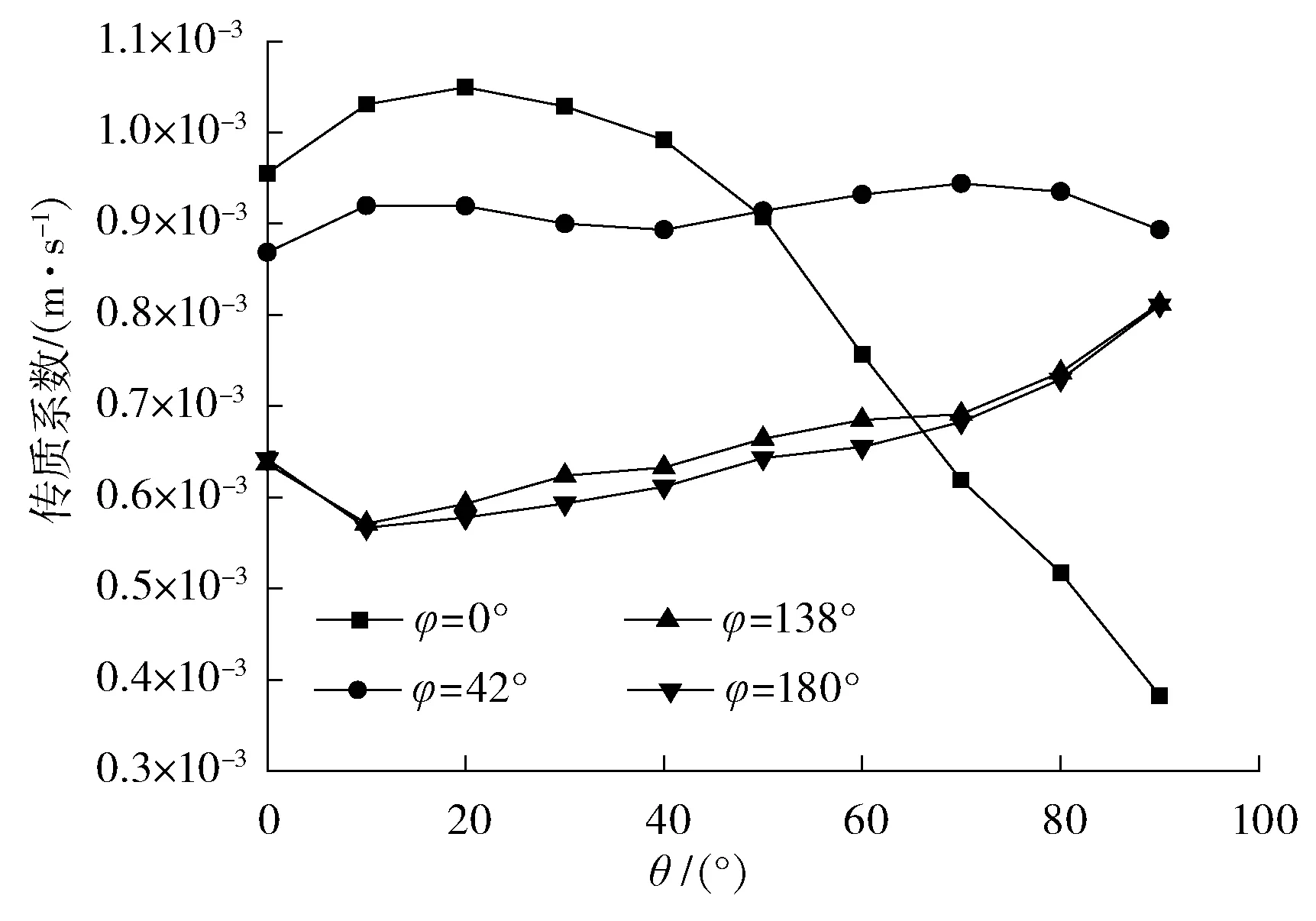
圖6 90°彎頭內各點的傳質系數

由圖5和圖6可得：傳質系數和速度的趨勢基本相同，隨著流體速度增加，傳質系數增大，與速度分布一致。沿著管道徑向方向，從內彎側到外彎側傳質系數整體呈現下降趨勢，內彎側的傳質系數達到最大值，外彎側的傳質系數整體較小。由于二次流的影響，內彎側的傳質系數急劇下降，在彎頭的出口達到最小值。

3.4 腐蝕速率的計算

反應速率常數和溫度滿足阿倫尼烏斯公式[13]：

K=A·exp(-E/RT)

(18)

式中：A為指前因子；E為表觀活化能，J/mol。

代入T=423.15 K，可求得K。經過上述計算，傳質系數在10-4～10-3m/s，對反應的影響遠大于反應速率常數，可將反應速率常數這一項忽略，簡化計算過程。

氧化膜厚度和孔隙率并不是固定的值，會隨著外界因素變化而改變。SANCHEZ-CALDERA L E等[16]發現當溫度高于120 ℃時，孔隙率會隨著溫度的增加而減小，并且給出了實驗數據，數據表明：當溫度接近150 ℃時，孔隙率為0.005，氧化膜厚度為10-6m；當溫度高于150 ℃時，氧化膜厚度主要與流體速度和pH有關。氧化膜厚度滿足以下關系式[15]：

(19)

式中：α為常數；pH為8～10。

圖7顯示了溫度為150 ℃、流體速度為3 m/s時，90°彎頭內各處的FAC速率。

圖7 90°彎頭內各點的FAC速率

FAC速率和各點速度的變化趨勢基本一致，速度越大，該處的FAC速率越大。為了確定理論計算結果的準確性，利用上述數學方程，通過模擬過程，計算得到t=25 ℃、pH為9.4、流體速度為3 m/s時的理論計算結果，并與ZHANG G A等[17]的實驗結果對比(見圖8)：沿著管道徑向方向，對于φ=0°時，ZHANG G A等的計算結果與筆者計算結果很接近；對于φ=180°的數據，兩者FAC速率變化趨勢基本一致，進入彎管，FAC速率略有減小，隨后一直保持增大的趨勢；沿流動方向，例如θ=45°時，此時內彎側的FAC速率最大，FAC速率從內彎側到外彎側逐漸減小，外彎側的FAC速率最小，兩者趨勢依舊基本一致。

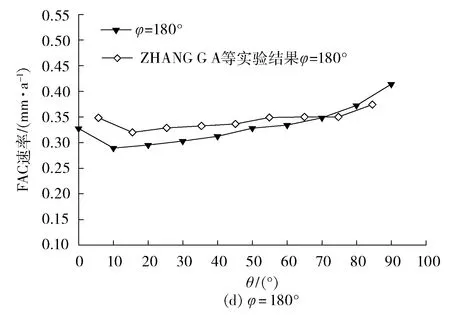
圖8 模擬結果與實驗結果對比

內彎側的腐蝕速率沿著流動方向減小，但是對于90°彎頭，腐蝕速率最大出現在內彎側，說明在電廠管道運行過程中，彎頭內側某處FAC程度最為嚴重，管子的壁厚最薄，此處管子破裂的風險最大。基于模擬結果，電廠需要對90°彎頭的內彎側加強監控和監測，及時更換彎頭。

4 結語

筆者研究了電廠90°彎頭的流場分布情況，根據模型計算FAC過程中的傳質系數與FAC速率，基于計算結果得到如下結論：

(1)流體剛進入彎頭，速度逐漸增大，到θ=20°左右達到峰值，由于內側發生二次流產生漩渦，使得內側速度迅速下降。除去彎頭內側附近區域，沿著管道徑向方向，流體速度從內彎側到外彎側逐漸減小，沿著流體流動方向，流體速度逐漸增大。

(2)90°彎頭內部各處傳質系數的情況與速度分布的情況基本保持一致，流體速度越大，流場內的湍流強度越大，傳質系數也越大。

(3)在90°彎頭內部，流體速度對FAC速率影響較大，流體速度越大，FAC速率越大。基于計算結果，最大FAC速率在內彎側，FAC速率最小在外彎側。