基于質量調諧技術的自旋彈丸姿態控制

楊 星,王 唯

(南京理工大學 瞬態物理國家重點實驗室， 南京 210094)

現階段有很多方法可以實現彈道控制，例如利用增阻減速型阻力執行機構結合自適應落點控制算法實現對彈丸射程的一維調控[1]、使用動力增程機構改變彈丸速度及運動方向[2]、以及通過舵翼附加氣動力矩改變姿態角進而引起彈丸氣動攻角和氣動力的變化[3-4]等。在理論上，采用氣動舵的控制精度較高，且可以實現連續調控；同時隨著技術水平和工藝的提高，舵機體積日益減小，因此采用舵機的有控彈丸的有效載荷相對較大。盡管上述方法存在諸多優點，仍舊有一些缺陷不可避免，例如增加舵翼作為獨立控制面時，受限于彈丸細長的外形，會在提供必要控制力(矩)的同時增加氣動阻力，使原有彈丸的有效射程大幅減小。因此，如何能在不改變氣動外形的前提下控制彈丸姿態運動進而實現彈道控制是現階段的研究熱點。

質量調諧技術[5]是一種利用附加的質量子系統平衡主系統受到的外力，用來減小主系統的受迫振動響應的方法。現階段國內外都致力于將智能材料引入傳統的質量調諧技術中[6]，例如電渦流質量調諧阻尼器[7]、混合動力調諧質量阻尼器(HATMD)[8]、杠桿式剛度可控阻尼器[9]等的出現，以及對傳統質量調諧結構的改造[10-11]，都預示著子系統中的阻尼器和彈性元件將不再局限于常規的彈簧和阻尼器。隨著相關技術的不斷發展，質量子系統性能的按需即時調節已經成為可能。在航海領域，如何應用主動控制技術實現振動控制是當下的研究重點[12-14]。盡管質量調諧技術調控精準、效果顯著，但在航空、航天等領域應用較少。

彈丸的姿態運動本質上可以簡化為陀螺的角運動，其主軸在空間中的方位可根據文獻[15]中提到的復球面理論映射到單位復球面上的點進行描述。如果彈丸內部存在一個類似陀螺的質量子系統與彈丸質心固聯重合，就相當于在復平面上增加一個具有等效質量的等效“質點”。將這個質量子系統與彈丸通過恰當的約束進行聯系，復平面內的雙“質點”系統在等效作用力的運動與通常意義上的質量調諧系統具有相似的特性。

本研究參考質量調諧技術的基本原理，提出了一種基于雙陀螺模型的姿態控制方法。基于選取的坐標系統，推導添加質量子系統的彈丸姿態運動模型。然后應用H∞控制方法推導姿態控制方程，以某型自旋穩定彈為例進行數值仿真，初步驗證了本文提出方法的可行性與有效性。

1 原理分析與動力學模型

1.1 坐標系統的選取

相關平動與轉動坐標系統的定義如下：

慣性坐標系Sg：本文使用的慣性坐標系與發射坐標系[16]的定義相同，其中坐標原點位于彈丸質心，xg軸在水平面內與初始射擊方向相同；yg軸豎直向上；zg軸在水平面內，且由xg和yg的叉乘確定。

彈體坐標系St：彈體坐標系與彈丸固聯，符合飛行力學的慣常定義[17]，坐標原點位于質心，各個坐標軸與慣性主軸重合，xt軸平行于彈體縱軸指向前；yt軸在彈體對稱平面內，垂直于xt軸向上；zt垂直于彈體的對稱平面，指向右。

為了區分彈丸與質量子系統，本文用x1t表示彈丸的彈體坐標系的橫軸，x2t表示質量子系統的本體坐標系的橫軸。

1.2 動力學模型

圖1 彈丸姿態運動坐標及廣義坐標定義

圖1中，α表示彈丸主軸與質量子系統主軸間的夾角；Δ表示速度與主軸之間的夾角，也就是氣動總攻角；xv軸的方向與彈丸質心速度方向一致；FD表示氣動阻力，方向與質心速度方向相反；FL表示氣動升力，方向與質心速度方向垂直；Ma表示氣動翻轉力矩。盡管通過速度坐標系定義主軸方向更為直接，但是拉格朗日方程在慣性系中具有最簡單的形式，因此這里的歐拉角都是相對慣性坐標系定義的。

根據坐標轉換原理[17]，彈體坐標系S1t相對慣性坐標系Sg的角速度在S1t中的投影為：

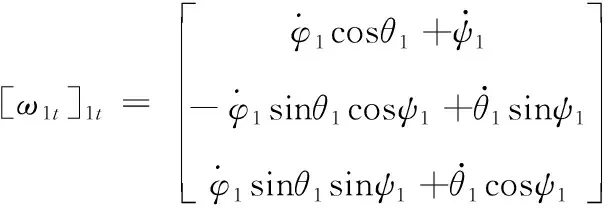
(1)

其中，符號[·]a表示向量在a坐標系中的投影。同理，可推導出與質量子系統固聯的本體坐標系S2t相對慣性坐標系Sg的角速度在S2t中的投影。

按照歐拉角定義，給出x1t在慣性坐標系中的投影：

(2)

將[x1t]g簡單地表示為x1。于是氣動總攻角可以通過向量內積表示為：

(3)

其中，V為彈丸質心的速度。

考慮氣動力矩的作用，升力FL和阻力FD分別通過升力系數Cl、零升阻力系數C0和阻力系數Cd確定；類似的，通過氣動翻轉力矩系數CMa可以確定氣動翻轉力矩Ma：

(4)

(5)

(6)

其中，Cl和Cd的量綱均為kg/m/Rad，C0的量綱為kg/m，Ma的量綱為kg/Rad。

選取φ1、θ1、ψ1、φ2、θ2、ψ2為廣義坐標，由于本研究只考察彈丸的姿態運動，所以沒有包含平動自由度。彈丸主軸與質量子系統主軸間的夾角α與廣義坐標的關系可表示為：

cosα=cosθ1cosθ2+sinθ1cosφ1sinθ2cosφ2+

sinθ1sinφ1sinθ2sinφ2

(7)

假定質量子系統與彈丸的慣性主軸分別與各自坐標系固聯且重合，且分別關于x1t軸和x2t軸對稱；同時假定二者的慣性矩在y1t、z1t和y2t、z2t方向上的投影相同，定義彈丸與子系統的各主軸的慣性矩在各自坐標軸上的投影依次為I1、I2、I2和J1、J2、J2。系統總動能可表示為：

(8)

假定氣流速度不變，選定θ1=0為零勢能參考平面，則系統的勢能可表示為：

(9)

其中，ks為兩系統間的彈性系數，量綱Nm/Rad；α0為一常數，量綱為Rad，表示彈性約束的平衡位置；

由此，由L=T-U求得拉格朗日函數為：

(10)

對方程式(3)進行變分運算，得到：

(11)

在姿態運動中，由于升力FL和阻力FD不做功，對姿態角沒有影響，由此可以得到總虛功的表達式為：

δW=|Ma|δΔ

(12)

則與各個廣義坐標對應的廣義力依次為：

(13)

(14)

Qψ1=Qφ2=Qθ2=Qψ2=0

(15)

其中，

(16)

容易看出，在式(13)～式(15)中，等式右端均包含了因式Δ/sinΔ。由于sinΔ出現在分母上，當Δ→0時，在數值計算中會導致Δ的相關項奇異。但是按照極限運動的基本規律，當Δ→0時，因式Δ/sinΔ→1。所以在下文的數值仿真計算過程中，將Δ作為自變量，為因式Δ/sinΔ編寫了一個自定義函數。該函數基于級數近似的方法，當Δ趨近于零時，通過計算有限項泰勒級數給出因式的近似值。

根據拉格朗日方程原理，得到添加質量子系統后系統在空間中運動的微分方程：

(17)

(18)

(19)

(20)

(21)

(22)

聯立式(17)～式(22)，即可確定包含質量子系統的彈丸的運動。

觀察式(10)，發現拉格朗日函數中不顯含ψ1和ψ2，對式(19)和式(22)兩邊積分，令：

(23)

(24)

其中，C1和C2均為常數。

為了簡化論證，在彈丸與質量子系統之間添加約束φ2=φ1+π。將其代入式(7)中，得到：

cosα=cos(θ1+θ2)

(25)

于是得到?α/?φ1=?α/?φ2=0和α=θ1+θ2。于是，方程式(17)和式(20可以分別整合并改寫為：

(26)

借助式(23)、式(24)和式(25)，簡化式(17)～式(22)，得到簡化的姿態運動模型：

(27)

(28)

(29)

其中，

μ=I2sin2θ1+J2sin2θ2

(30)

2 控制器設計

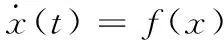
(31)

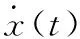
依照H∞控制設計，將式(31)整理成下面的狀態依賴的類線性微分方程：

(32)

其中：w(t)為外界擾動；z(t)為輸出向量；矩陣A、B1、C1是與x(t)相適應的函數矩陣。在一般的H∞控制問題中，對于給定的標量γ，令γ>0，當且僅當x(0)=0時，有如下關系：

(33)

如果系統滿足上述條件，則可以稱系統的L2增益小于等于γ，根據現有理論可以給出使系統穩定的哈密爾頓——雅克比不等式(Hamilton-Jacobi-Isaacs，HJIs)，根據舒爾補引理(Schur complement)，可將HJI轉化為系統的有實界不等式，用于控制器的求解。具體的推導過程參考文獻[18]，下面設計適用于包含質量子系統的彈丸姿態控制器。

引入H∞控制器，則狀態空間中的系統方程可表示為：

(34)

其中：y(t)為輸出向量；z(t)為表現控制器作用的性能向量；u是控制輸入，同時也是控制器的輸出信號。矩陣Cs和Ds用來平衡y(t)和z(t)，且所有向量和矩陣都具有與輸入輸出信號數量相適應的維數。

設計與系統相適應的狀態反饋控制器K。令u=Ky，當存在標量γ，使如下有實界不等式

(35)

X>0

(36)

其中，M(x)=AX+B2W+(AX+B2W)T。當線性矩陣不等式(35)和不等式(36)有可行解W*時，u=W*(X)-1x就是系統的一個狀態反饋H∞控制器。

3 數值仿真

本節運用Matlab進行數值仿真，驗證提出方法的有效性。

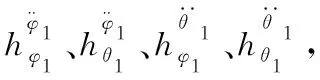
C1=C2=I6

D11=D12=D21=06×1

其中，I3,3表示3×3的單位陣的第3列；aij(i=1,…,6，j=1,…,6)分別為：

借助PBH秩判據，驗證本研究提出系統的可控性和可觀性。代入矩陣，可得：

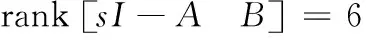
(37)

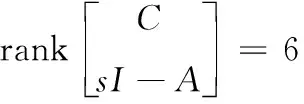
(38)

因此，文中提出的包含質量子系統的彈丸姿態運動模型滿足完全可控性和完全可觀性。

給定模型中相關參數(見表1)，按照式(35)中的約束條件，求解狀態反饋控制器。

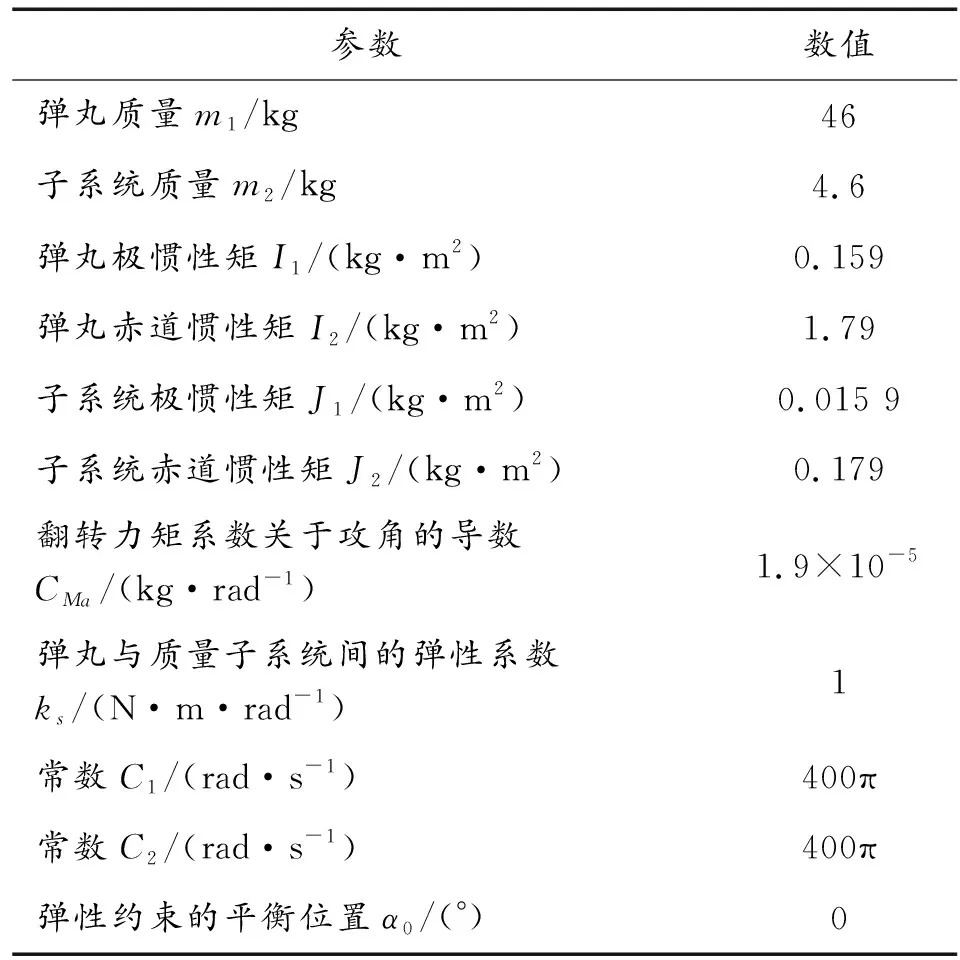
表1 相關參數

應用Matlab中的LMI工具箱求解控制器，得到控制矩陣K。仿真結果如圖2所示。

由圖2可以看出，添加控制器后，φ1的結果呈周期性振蕩，θ1的振幅減小。由此可以看出，添加子系統后，受控彈丸的主軸偏離慣性坐標橫軸的角度減小。

4 結論

基于質量調諧技術的作用原理，提出通過在彈丸內部增加一個類陀螺結構的質量子系統的方法對自旋彈丸進行姿態控制。仿真結果表明，添加質量子系統后，彈軸偏離平衡位置的幅度明顯減小，驗證了方法的有效性。今后將繼續探究質量及系統對彈丸姿態運動的影響機理，以及將此模型用于調控彈丸姿態的非線性控制設計。

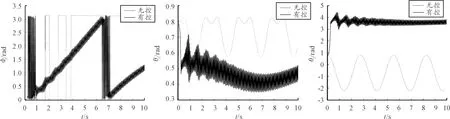
圖2 添加質量子系統的彈丸的姿態運動