控制器故障下固定翼無人機的姿態控制
唐 余,劉永春,曹立佳,林 達,4,劉小芳
(1.四川輕化工大學 a.自動化與信息工程學院; b.物理與電子工程學院; c.計算機學院, 四川 宜賓 644000;2.四川省人工智能重點實驗室, 四川 宜賓 644000; 3.四川省智慧旅游研究基地, 四川 自貢 643000;4.徐州工程學院 信電工程學院, 江蘇 徐州 221111)
在當今社會的各個領域中,無人機已得到了廣泛的應用[1-2],并將完成更多的任務。無人機經常進行高空長時作業,脫離人的直接操縱,在干擾或機體損傷的情況下,無法進行人工處理,其本身必須具備一定故障和失效的應對能力[3-4];但是,一旦控制器故障超出無人機應對能力范圍,其飛行品質不可避免要降低,需要立即采取措施,可以通過設計可重構控制系統[5-6]來保證飛機安全。
可重構控制(Reconfigurable Control,RC)系統通常包括故障檢測(Fault Detection,FD)系統[7-8]和控制器重構(Controller Reconfiguration,CR)系統[9-10],并能夠與自適應控制器[11](Adaptive Controller,AC)相結合。
針對AC的設計,文獻[12]采用反步積分法,這種方法在傳統反步方法的基礎上添加了跟蹤誤差的積分項,以此來彌補穩態誤差;文獻[13]提出采用動態逆方法,只需要構建出無人機的狀態空間模型,即可同時求解出所有所需的控制器,極大的提高了運算效率;結合這兩種方法的優點,得到一種增加誤差積分項的動態逆方法,既能彌補穩態誤差,又方便構造無人機控制器。
關于FD系統的設計,文獻[14]提出采用構建多模型自適應估計(Multiple Model Adaptive Estimation,MMAE)的方法,它是基于一組并行的卡爾曼濾波器,其特點是每一個特定的故障都有一個相應的卡爾曼濾波器與之對應。
關于CR系統的設計,文獻[9,13,15]提出采用控制分配方法,能在不增加冗余控制器的情況下結合無人機模型的性質構造出虛擬控制信號,然后通過其與正常控制器和故障控制器之間的相互關系重構無人機控制器。
AC能根據飛機的飛行情況實時地產生控制信號,具備一定的被動容錯能力;但是,當一些故障超出其容錯能力范圍時,就需要FD系統能及時監測到這些故障行為,并為CR系統提供相關參數,CR系統利用這些參數并結合自適應控制器重新構造控制命令。
1 固定翼無人機建模
無人機的姿態在空間中的運動具有3個繞質心旋轉的自由度,分別為滾轉、俯仰和偏航運動;其副翼和升降翼相互作用產生滾轉力矩和俯仰力矩,方向翼和副翼相互作用產生偏航力矩。
如圖1所示,無人機的姿態運動涉及慣性坐標系、機體坐標系和氣流坐標系,分別以字母n、b和w表示。其中α和β分別為無人機的攻角和側滑角,可由下式求得:
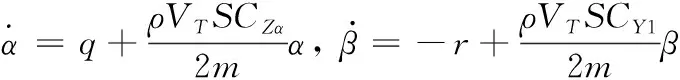
(1)
式(1)中:m是無人機質量,其余參數見下文介紹。
考慮無人機相對于慣性坐標系的滾轉、俯仰和偏航姿態角分別用歐拉角φ、θ和ψ表示,無人機相對于機體坐標系的姿態角速度分別以p、q和r表示。這些變量之間的關系如下:
(2)
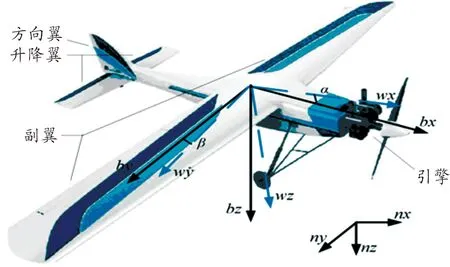
圖1 固定翼無人機模型及坐標系
根據牛頓力學可推導出無人機姿態系統的動力學方程為:
(3)
式(3)中:Ib是無人機的轉動慣量矩陣,并且Ωb=[pqr]T。
(4)
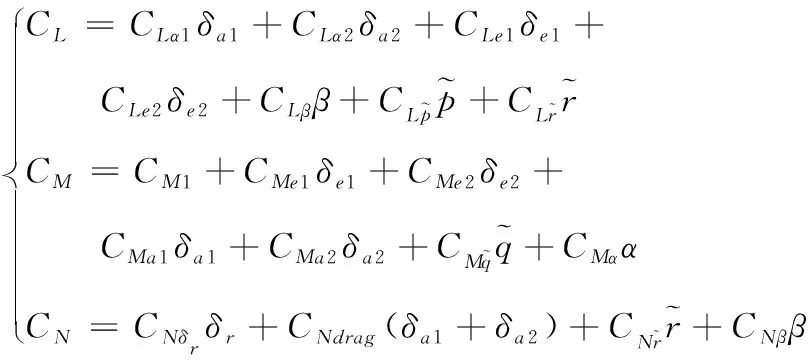
(5)
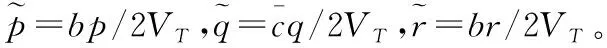
考慮到建立無人機姿態系統的矩陣模型,可以令:
x=[pqr]T,u=[δa1δa2δe1δe2δr]T
(6)
根據式(6),式(3)可以被重寫成:
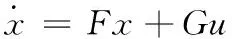
(7)
式(7)中:
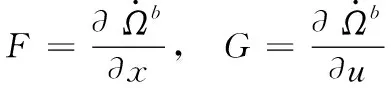
(8)

表1 仿真所需的固定翼無人機模型參數
2 可重構控制系統設計
可重構控制系統包括故障檢測和控制重構部分,可與自適應控制器相結合,能及時檢測到故障并重構無人機控制器。
圖2中的xk+1/k+1和xd分別為x的估計值和期望值;pi(k)為控制器i發生故障的概率;δi,fault為控制器δi的故障狀態;uf為無人機的實際控制輸入;Cv為虛擬控制信號。
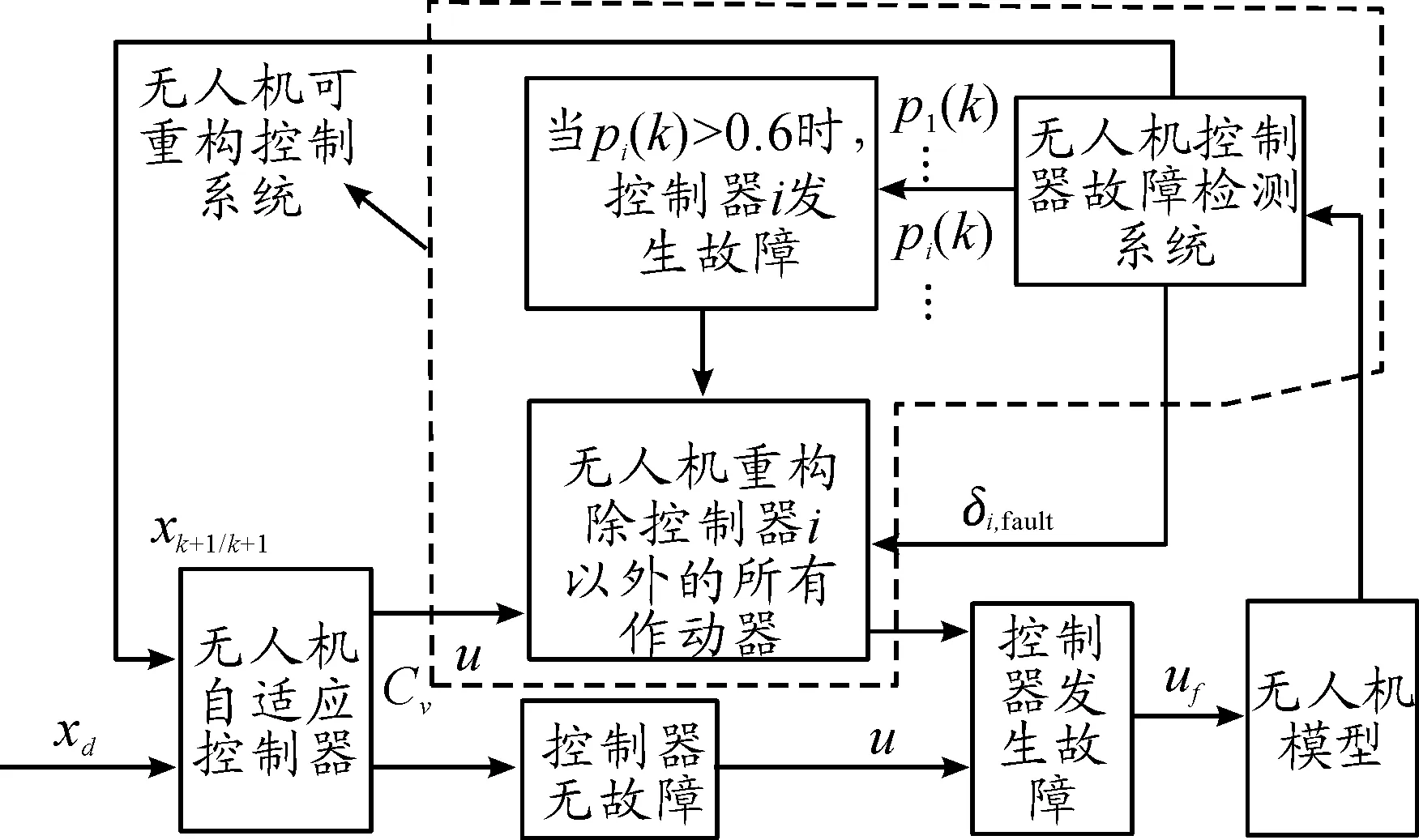
圖2 無人機可重構控制系統
2.1 無人機自適應控制器設計
根據動態逆方法[15]并基于Lyapunov原理設計控制器向量u。
針對式(7),定義跟蹤誤差及其積分項:
(9)
根據式(9)定義一個Lyapunov函數為
(10)
式(10)中:λ>0,且V(K,e)≥0,即正定;并且,對式(10)求導并代入式(7)可得:
(11)
(12)
式(12)中:k>0,λ>0;F和G見式(8)。
2.2 無人機控制器故障檢測系統設計
采用組合擴展卡爾曼濾波器[15]的方法檢測控制器故障;其基本結構如圖3所示。

圖3 控制器故障檢測系統基本結構框圖
針對控制器無故障的卡爾曼濾波器設計,首先將式(7)離散化后,用狀態空間法表示為
(13)
式(13)中:xk、Fk、Gk和uk分別為其第k步長時刻的采樣值;h為系統的采樣間隔或步長;wk為零均值離散隨機噪聲,用以描述姿態系統中的不確定性。
姿態系統測量方程的離散形式可以被描述為
yk=Cxk+vk
(14)
式(14)中:C為觀測矩陣;vk為零均值離散隨機噪聲,用以描述測量過程中的不確定性。
控制器無故障下的擴展卡爾曼濾波器設計流程如下:
(15)
式(15)中:xk/k為當前時刻的狀態估計值,xk+1/k為其下一時刻的預測值;xk+1/k+1為狀態估計值的更新。Pk+1/k是狀態誤差協方差矩陣的估計值;Pk+1/k+1是狀態誤差協方差矩陣的測量更新;r是測量值與估計值之間的殘差;Lk是第k步長卡爾曼增益矩陣。Rw,k和Rv,k分別為wk和vk的協方差矩陣。
針對控制器故障下的卡爾曼濾波器設計,假設需要檢測u中的第i個控制器故障與否,一個狀態向量可以被重構為
(16)
(17)
式(17)中:G(i)為取G的第i列。G(0,i)表示將G的第i列置零。
重構后的姿態離散化后可表示為
(18)
式(18)的觀測矩陣為:
yzik=Cfzik+vfk
(19)
式(19)的卡爾曼濾波器設計與式(15)相似,只需要將其中的x、Fk、Gk、C替換成zi、Fzi、Gzi和Cf。
設定概率密度為高斯函數,其表達式為:
p[y=yik|(δ=δi)]=
(20)
最后,通過下式即可估計控制器故障概率:
pi(k)=p[δ=δi]=
(21)
式(21)中:p0(k)為無故障概率;p1(k)~p5(k)分別為δa1、δa2、δe1、δe2、δr故障概率。
2.3 控制器重構系統設計
空氣動力系數具有如下式的關系。
(22)
為了方便重構控制器,可以根據式(5)和式(22)構造虛擬控制指令為:
(23)
式(23)中:δa1、δa2、δe1、δe2和δr均由無人機自適應控制器提供。
情況1:針對單控制器故障,以δa1故障為例,其重構后的各控制器如下所示:
(24)
同理,其余單控制器故障的控制重構方案設計同式(24)。
情況2:針對雙控制器故障,以δa1、δa2同時發生故障為例,其重構后的各控制器如下所示:
ξ1=(CM-CMa(δa1,fualt+δa2,fualt))/CMe
ξ2=(CL-CLa(δa2,fualt-δa1,fualt))/CMe
δe1=(ξ1-ξ2)/2,δe2=(ξ1+ξ2)/2
δr=(CN-CNdrag(δa1,fualt+δa2,fualt))/CNδr
(25)
同理,其余雙控制器故障的控制重構方案設計同式(25)。
3 仿真與分析
實驗仿真平臺為Matlab,固定翼無人機相關物理參數如表1所示。
為了驗證無人機可重構控制系統在復雜運動下的有效性,設無人機飛行狀態為趨于一定高度的螺旋上升運動。設置3組仿真實驗,其中兩組仿真實驗都是在相同的控制器故障下完成,一組在只為無人機提供自適應控制器,另一組則增加了可重構控制系統系統,這兩組仿真實驗將會一起與無控制器故障下的無人機仿真結果作對比;以此來分析可重構控制系統的有效性。
相關仿真結果如下:由圖4、圖5和圖6可知,在時間段T1、T2、T3、T4、T5上控制器δa1、δa2、δe1、δe2、δr分別發生卡死故障,特別地,T2、T3、T4、T5均在T1內,在這種情形下,相比于單純的自適應控制器(AC),增加了可重構控制系統的自適應控制器(AC-RC)能在極短的時間內檢測出故障并重構無人機控制器,使無人機姿態控制更接近于理想情況,即無故障情形下的姿態跟蹤;如式(5)所示,CL、CM、CN分別為控制無人機力矩的重要參數,只要這些參數相對于無故障情況下的變動不大,無人機的姿態就能以接近于無故障情況的運動,在圖7中,當故障來臨時,相比于AC,AC-RC能使這些參數在極短的時間內收斂于無故障情況,進而達到如圖5所示的控制效果。
4 結論
由上述仿真結果可知,提出的可重構控制系統能及時檢測出無人機控制器故障,并根據檢測出的故障類型,在不增加冗余控制器而在原有健康控制器的基礎上自主地進行控制器重構,進而達到理想的控制效果。通過與自適應控制器(AC)在故障情況下的控制效果進行比較,充分說明該系統對無人機姿態的控制效果更為理想,更接近于無故障情況下的控制效果。
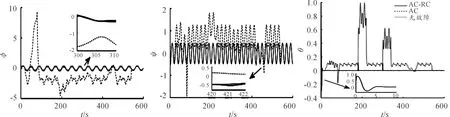
圖4 三種控制模式下的無人機姿態角曲線
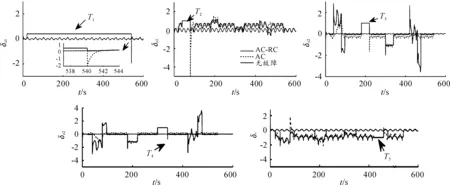
圖5 三種控制模式下的無人機控制輸入曲線
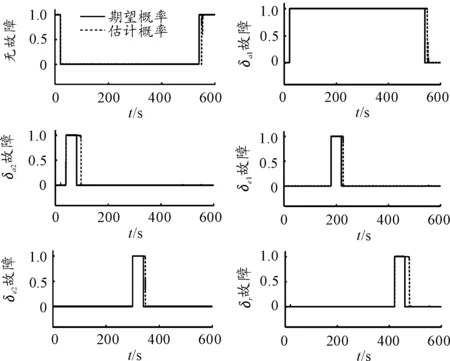
圖6 無人機控制器故障概率估計曲線

