格林公式教學探討

劉華 方曉峰 景慧麗

【摘要】格林公式是多元函數積分學中的一個非常重要的公式，其理論意義及使用價值都值得關注.本文采用“內容分解—分層推進—協作探究”的教學策略構建格林公式，收到了比較好的教學效果.

【關鍵詞】格林公式;協作探究;創新能力

1825年，英國數學家格林個人出版了一本數學小冊子——《數學分析在電磁學中的應用》，在這本小冊子中最早出現了格林公式.由此可見，其產生的背景是電磁學，但學員對電磁學這一物理背景并不熟悉.如果通過物理背景講述格林公式的建立，在背景知識的講解上會浪費不少時間，而且達不到預期效果.因此，本文將從幾何的角度，基于學員目前的知識結構，從學員熟悉的問題出發建立格林公式.

一、格林公式教學設計現狀

關于格林公式教學大家關注的也比較多，梳理一下大概有以下幾種情形：

一種就是按照《高等數學》教材上的思路，由一元函數積分學中牛頓-萊布尼茲公式推廣到多元函數積分學，直接給出公式然后進行證明.這種教學思路對學員來講難以理解，從一元到多元的推廣并不是那么自然，有時還存在一定的問題.因此，這種類比推廣并不像二元向多元推廣那么容易接受.

另一種是采用猜想、驗證的思路讓學員體驗格林公式的建立過程.無疑猜想、驗證是數學研究常用的一種方法，但這種方法對格林公式而言并不是那么適合.這種猜想、驗證是按照特殊到一般的總體思路，讓學員去猜想格林公式的具體形式，然后再證明.但格林公式中被積函數之間的關系并不是那么簡單，從特殊的情況很難猜想到公式的具體形式.不少教員在設計這個猜想環節時都很牽強，更像是已知結果而猜想結果.

二、探究式格林公式教學設計

為使學員清楚格林公式的來龍去脈，讓學員參與到格林公式的建立過程中，通過協同探究讓學員逐步發現、建立格林公式，體會數學概念的建立過程.

（一）格林公式中兩類積分積分區域之間關系探究

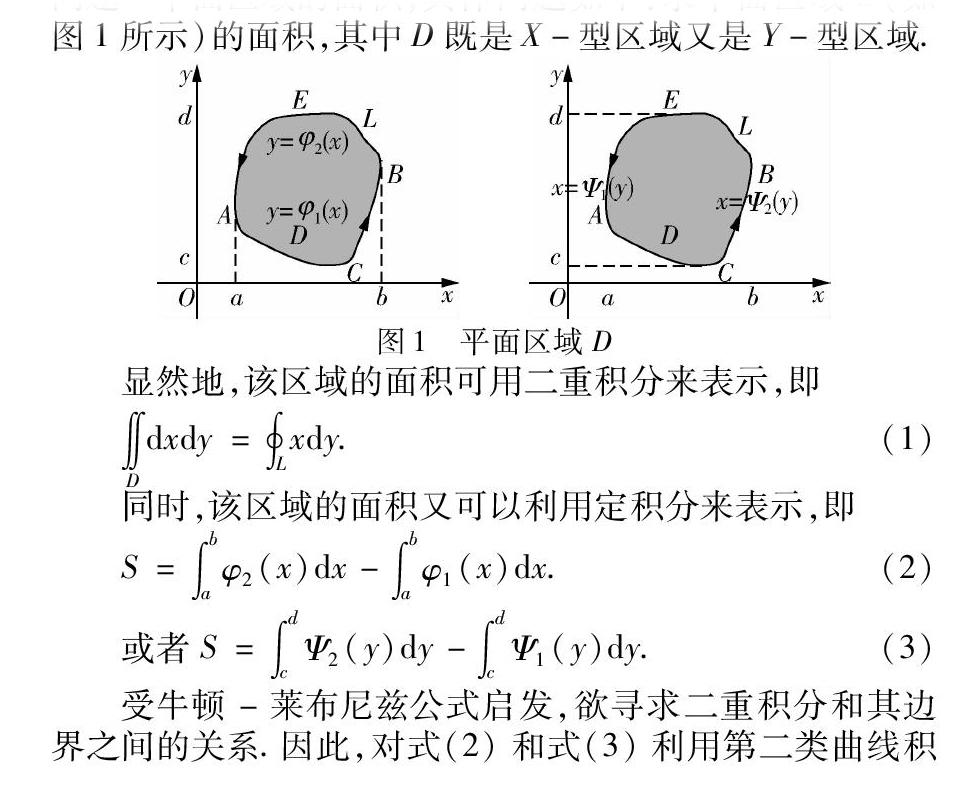
遵循由特殊到一般的研究思路，從二重積分積分區域的特殊情形出發進行探討.問題出發點為學員熟悉的幾何問題—平面區域的面積，具體問題如下：求平面區域D（如圖1所示）的面積，其中D既是X-型區域又是Y-型區域.

三、結束語

采用“內容分解—分層推進—協作探究”的教學策略實施格林公式教學，能讓學員體會到數學公式的建立過程，培養學員的數學思維，增強學員的探索意識和求知欲望，從而提升學員的創新能力.

【參考文獻】

[1]同濟大學數學系.高等數學[M].北京：高等教育出版社，2014.

[2]薛蓮，李洵.格林公式的研究性教學嘗試[J]，牡丹江大學學報，2008（11）：137-139.