基于R/S分析的阿壩藏族羌族自治州年降雨量定量預測
陳江峰,龔書浩,李迎超
(1.河南理工大學 資源環境學院,河南 焦作 454003;2.河南省核工業放射性核素檢測中心, 河南 鄭州 450044; 3.黃河交通學院,河南 武陟 454950)
降雨量是水循環過程中最重要、最活躍的因素之一,降雨量的分布會直接影響到徑流等水文環境,同時降雨量也是描述一個地區氣候變化的關鍵指標,一個地區降雨量的多少對當地氣候環境、水資源分布、生態系統等都會產生重要影響。由于降雨等自然現象具有突發性,在發生時間上存在不規則性,降雨量的大小又受多種復雜因素的影響,因此很難對降雨量進行精準預測。近年來,國內外研究人員發現,看似無序、不規則的降雨現象實際并不是完全隨機的,而是蘊含著規律,比如自相似性,這是傳統理論難以解釋的,因此越來越多的學者開始利用分形幾何學等理論來探討降雨現象的發生規律。
Hurst提出的重標度極差法(R/S分析法)是分析時間序列的有力工具,是分形理論的重要方法之一[1],其優勢在于無論時間序列是正態分布還是非正態分布,分析結果的穩定性均不受影響,因此迄今仍然是估計Hurst指數時最常用的方法[2]。R/S分析法以其能夠描述非線性時間序列復雜變化內在規律的特點,在水文學和氣象學研究中有著廣泛應用[3-4]。目前利用R/S分析法研究時間序列取得了很大進展,但這類方法的研究與應用對象均是時間序列的趨勢性分析,屬于定性預測。本研究在R/S趨勢性分析研究的基礎上,考慮時間序列長度和相關性等因素,輔以計算機技術,實現了降雨量的定量預測。
1 理論基礎
1.1 β-Z-H三參數綜合趨勢分析
1.1.1 Mann-Kendall檢驗
Mann-Kendall(M-K)檢驗法是一種非參數統計檢驗法,廣泛適用于非正態分布特征變量的趨勢分析。設x1,x2,…,xn為時間序列數據,n為時間序列數據的長度,對于所有t、τ≤n,且t≠τ,xt和xτ的分布是不同的,M-K法定義統計量S為
(1)
其中
式中:xt、xτ分別為序號t、τ對應的時間序列數據。
S的方差Var(S)計算公式為
Var(S)=[n(n-1)(2n+5)-
(2)
式中:i為時間序列數據出現的次數;ei為時間序列數據出現次數的個數。

(3)
在M-K檢驗中,另一個非常有用的指數為肯德爾斜率β,它表示時間序列趨勢大小,若β>0,則為上升趨勢,若β<0,則為下降趨勢,若β=0,則說明趨勢不明顯[6]。β值計算公式為
(4)
1.1.2 Hurst指數
R/S分析的基本思想是改變樣本序列的時間尺度,研究其在不同尺度范圍內的統計規律,從而進行大小時間尺度間的相互轉換[7-8]。該方法能從分形時間序列中區分出隨機和非隨機序列。通過Hurst指數的判定,可以判斷出時間序列的分形結構和狀態持續性,為時序的復雜性演變提供一種有效的非線性科學預測方法[9]。
對于一個隨機過程樣本序列,如果其物理量的時間序列為x1,x2,…,xn,滿足
(5)
式中:τ為時間序列的序數;R(τ)為時間序列對應的累積偏差的域;S(τ)為R(τ)對應的標準偏差;R(τ)/S(τ)為重標極差;H為Hurst指數,其值介于0到1之間[10],可以在雙對數坐標系中根據[lnτ,ln(R/S)]的值用最小二乘法擬合求得。
若H=0.5,則表明現在和未來之間沒有相關性;若0 對一個具有狀態持續性的時間序列來說,具有長記憶效應特征。從理論上講,今天所發生的一切將一直影響未來,即存在對初始條件的敏感性[12],對時間序列做Vτ~lnτ分析,即 (6) 此時Vτ圖像對應τ的循環變化長度是時間序列持續性的平均長度,是統計意義上的數值,而非時間序列的真正周期,也是預測初始序列長度選取的可行值[13]。當圖中有多個拐點時,遵循最大H值且擬合度較高的原則選擇突變點作為循環長度的平均值[13]。 H值反映了時間序列的趨勢性,若0 (1)對時間序列進行R/S趨勢性分析,得到線性回歸方程ln(R/S)=a0lnτ+a1,將ln(τ+1)代入線性回歸方程,得到回歸方程下一點的最優值ybest。 (2)將假設數據x(τ+1)作為下一點的新數據代入相關計算機程序中進行運算,得到新的預測點值ln(R/S)τ+1,判斷|ln(R/S)τ+1-ybest|<Δt是否成立(Δt可以根據需求賦值,以誤差最小、預測精度最高為準則)。如成立,則此時的x(τ+1)即為定量預測點,程序停止運行,輸出x(τ+1),否則進行下一步。 (3)若上步不滿足,則程序再次改變迭代數據,通過連續運算輸出滿足要求的原始數據,即為誤差范圍內距離ybest最近的原始數據,即為下一點的定量預測值x(τ+1)。 阿壩藏族羌族自治州地處青藏高原東南緣、橫斷山脈北端與川西北高山峽谷的接合部,氣溫分布自東南向西北隨海拔升高而降低:海拔2 500 m以下的河谷地帶降水集中、蒸發快,為干旱、半干旱地帶;海拔2 500~4 100 m的坡谷地帶為寒溫帶,年平均氣溫1~5 ℃;海拔4 100 m以上為寒帶,終年積雪,長冬無夏。本研究采用阿壩州小金水文觀測站實測年降雨量數據(1961—2000年)進行分析和預測(圖1)。 圖1 阿壩州年降雨量變化曲線 對年降雨量數據進行R/S趨勢性分析,得到H=0.663 1、R2=0.945 2,表明該時間序列具有正持續性,時間序列在未來的增減性與原來是相同的,但持續性較弱,如圖2所示。 將年降雨量數據帶入M-K檢驗公式(1)~(4)中得到Z=0.338,β=1.532。β是評價時間序列歷史發展趨勢的指標,Z可以反映其顯著程度,H能反映時間序列未來發展的持續性。β、Z、H都是對時間序列進行分析的指標,進一步將三者綜合,則不同的數值對應關系 圖2 年降雨量R/S趨勢預測 具有不同的指示意義。在α=0.05置信水平上,β-Z-H三參數綜合分析對降雨演化特征的指示作用如表1所示。 表1 β、Z、H綜合分析的指示作用 根據之前得出的Z=0.338,β=1.532,H=0.663 1,結合β、Z、H綜合分析指示作用表分析知,研究區年降雨量時間序列符合序號7的特征,即降雨量過去是增加的,未來將持續增加,但是趨勢不明顯,這與R/S趨勢分析得到的結果是相同的。 如果初始序列長度過大,數據的波動性將會增強,回歸方程的線性關系就會減弱,因此選取合適的初始序列長度對預測結果的準確性尤為重要。對上述時間序列做Vτ~lnτ分析(圖3),時間序列循環變化長度為12,因此選取12為時間序列預測的初始長度。 圖3 降雨量時間序列長記憶性分析 記1982—1993年降雨量數據為序列A,以后新的序列依次命名為序列B、C等。對該時間序列進行R/S分析,得到回歸方程如圖4所示,H=0.548 17,R2=0.977,那么R/S趨勢預測點之間存在良好的線性關系,可以嘗試對該時間序列進行定量預測,得到的預測值x(13) 為628 mm。 圖4 序列A的 R/S定量預測 將x(13)放入序列A中得到序列B,對序列B進行同樣運算,得到預測值x(14)=637 mm(圖5)。同理,得到序列C(圖6),預測值x(15)=636 mm。 圖5 序列B的R/S定量預測 圖6 序列C的R/S定量預測 對得到的預測值與真實降雨量進行精度檢驗,結果見表2。 表2 初始序列長度為12的定量預測值與真實值對比 將預測值與真實值對比可以看出,初次預測和第二次預測結果較為理想,特別是第一次預測精度為97.6%,但是第三次較前兩次誤差增大,說明隨著預測時間序列長度的增加,時間序列的波動性增強,內在規律性減弱。總體而言,模型預測的平均相對殘差為7.1%,平均預測精度為92.9%,預測效果顯著。 (1)輔以計算機技術,實現了R/S分析方法的定量預測,將非線性時間序列問題進行了線性求解,將該模型應用于降雨量預測,平均精度高達92.9%。 (2)R/S定量預測與初始序列長度有關,連續多次預測會使模型精度有所降低,因此對時間序列長度的選擇進行分析,顯得尤為重要。 (3)隨著人類活動的日益增強,降雨量大小預測變得更為復雜,運用R/S分析對降雨量進行定量預測,可為非線性時間序列問題的解決提供一種快速而有效的方法。1.2 初始序列長度
1.3 R/S定量預測方法的基本原理
2 R/S定量預測實例
2.1 數據來源
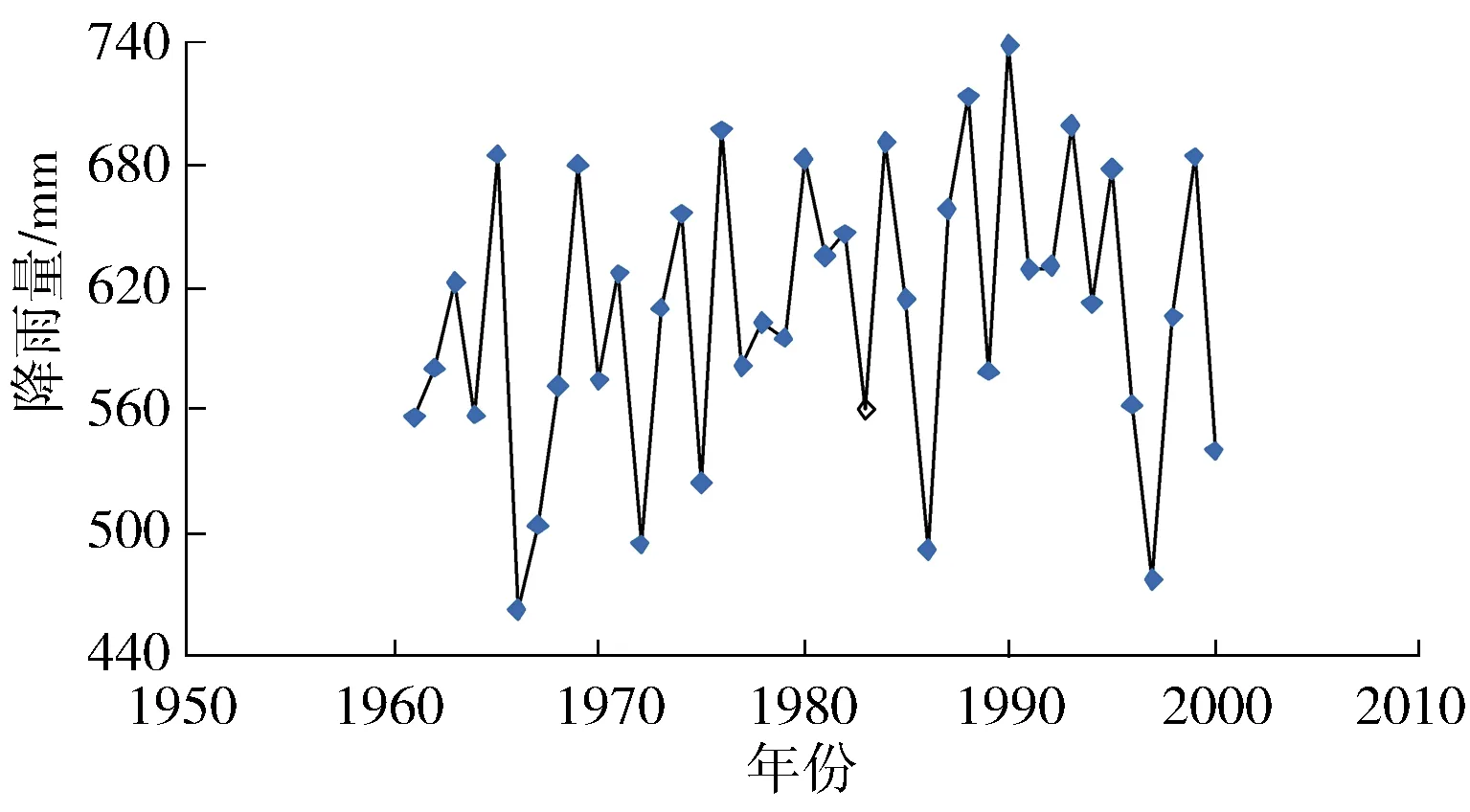
2.2 年降雨量β-Z-H三參數綜合趨勢分析


2.3 初始序列長度

2.4 R/S定量預測



2.5 預測精度檢驗

3 結 論

