液壓四足機器人設計沖突消解方法研究

秦建軍，路可欣，江 磊，蘇 波

(1.北京建筑大學 機電與車輛工程學院城市軌道車輛服役性能保障北京重點實驗室， 北京 100044；2.中國北方車輛研究所， 北京 100072)

在產品概念設計階段，對產品方案單元配置進行方法研究，可以大大改善對不同特定功能的響應程度，得到更為滿足要求的元件配置結構，提高研發效率，縮短開發周期，增強產品核心競爭力。

液壓四足機器人因其具有突出的非結構地形適應能力、功率密度比高等特點得到了廣泛關注，以美國波士頓公司研發的Big dog液壓四足機器人為例，其具有冰面、崎嶇地形等地形通過性以及抗外部大沖擊下的自平衡能力，意大利研究院研發的HyQ進一步實現了機器人在不同環境下的周期性跳躍。與此同時，國內學者也進行了大量研究，上海交通大學田興華等[1]根據液壓四足機器人的運動性能，在不同的地形中提出了三種不同的混聯腿結構構型，同時進行了MATLAB與ADAMS的聯合應用仿真研究；為提高機器人腿部柔順性，華中科技大學于匯洋[2]在踝關節與趾關節之間引入韌帶元件，同時將鏈式傳動應用在腿部結構的髖關節和膝關節上，以此來降低腿部的轉動慣量；山東大學榮學文[3]、朱彥防[4]提出對SCalf機器人每條腿配置四個主動自由度，實現了多種步態的隨機轉換；為進一步實時跟蹤機器人腿部關節的運行情況，西北工業大學張學峰等[5]針對液壓四足機器人在非結構化地形中的高機動需求，提出了運用PD迭代控制算法。由此可以看出，液壓四足機器人的腿部結構研究主要集中在算法與建立數學模型等方面，但在實際的元件配置中，會出現元件之間的相互沖突以及元件間相互制約的現象，難以實現腿部結構多次優化，為此提出了沖突元件消解方法與結構創新設計。

1 設計結構矩陣

設計結構矩陣(Design Structure Matrix,DSM)建立模型可描述元件間關系，可用有向圖表示，其中有向圖是由多個節點間的有向線段構成，運用有向圖可以描述產品設計結構矩陣中各元素之間的關系，根據各個信息流動方向，可分為順序(從屬)、并行(獨立)、耦合(共生)、條件(偶然)這四種關系。

1) 順序(從屬)：配置元件間具有前后的依賴關系，前面的任務輸出信息時，后面的任務才能開始執行。

2) 并行(獨立)：配置元件間分別獨立執行，各配置元件不存在必然聯系。

3) 耦合(共生)：該關系在產品配置過程中應用的最為普遍，在產品配置設計過程中占主要影響因素，配置任務間存在相互依賴關系，各配置任務間存在眾多信息交互現象，通常通過多次反復迭代才能完成。

4) 條件(偶然)：配置元件間具體的流向可以選擇，且均可完成配置任務。

若需要進一步識別各元件間耦合任務集，定義配置元件耦合強度指數CII(Coupling Intensity Indicator)，其定義式為

CII=CIIt-CIIu

(1)

式中：CIIt為配置元件耦合集內部耦合平均值，CIIu為所有配置元件耦合平均值，其中CIIt與CIIu的定義式分別為

(2)

(3)

式中：oij為配置元件耦合的關聯程度，r為首個配置元件在矩陣中行(列)序號，n為末端配置元件在矩陣中行(列)序號，s為配置元件總數，在給定閾值的情況下，通過配置元件耦合強度可得到所有耦合集。

2 基于設計結構矩陣的功能結構聚類的元件沖突消解

2.1 研究方案

本文的研究理論主要基于設計結構矩陣與分支拓撲樹結構方法，對含沖突元件的聚類矩陣進行劃分，得到滿足特定功能的最優產品元件配置，其主要方案可分為4個關鍵步驟。

步驟1 對含沖突元件的設計結構矩陣進行聚類。用有向圖表示元件配置關系，運用布爾代數算法將其與沖突矩陣進行累加，得到設計結構聚類矩陣，優化產品流程，迭代次數得以減少。

步驟2 基于產品設計結構矩陣建立分支拓撲樹結構。將設計結構聚類矩陣與典型分支拓撲樹結構進行映射，轉化為分支拓撲樹圖論的分解結構，以便對最優方案進行評價與遴選。

步驟3 基于產品設計結構矩陣聚類的評價分析。在設計結構矩陣中進行模塊劃分，遵循高內聚低沖突的聚類原則，根據該原則對多方案進行評價與遴選，得到最優方案。

步驟4 基于分支拓撲樹的粒度層級分析確定最終元件組合。將最優方案進行進一步子模塊劃分，與多種算法結合使用，使數據簡潔，冗余信息最小化以得到滿足需求的最終配置元件組合。

以液壓四足機器人為例，其腿部結構的功能結構聚類創新流程框圖如圖1所示，將機器人腿部多個元件進行設計結構聚類分析，通過沖突指數與內聚度這兩個評價指標遴選出最優腿部設計方案，對該方案進行粒度層級分析，得到最終的配置元件子模塊，在此基礎上生成液壓四足機器人腿部結構設計的創新方案。

2.2 基于設計結構矩陣的沖突元件聚類方法

產品設計早期是一個動態且復雜的設計流程，為實現后期元件的聚類裝配，在該階段應根據元件間的關系構建設計結構矩陣，同時要考慮元件的相互沖突以及相互制約的問題，本節提出了基于設計結構矩陣的沖突元件聚類方法。

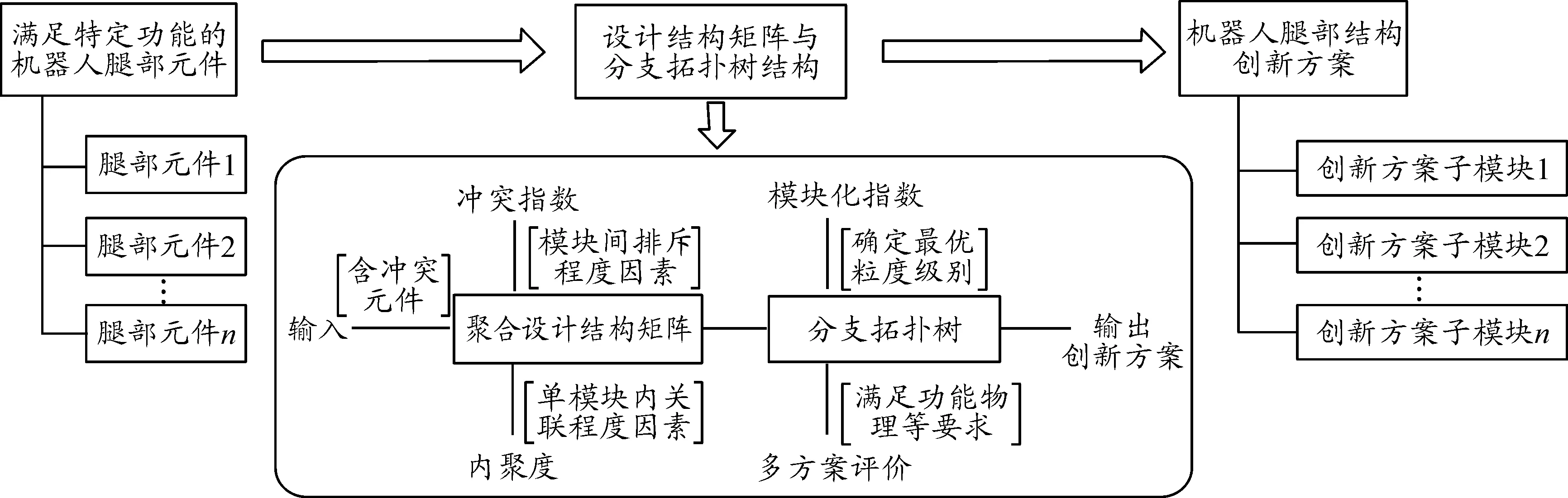
圖1 液壓四足機器人腿部結構的功能結構聚類創新流程框圖

有向圖對應的鄰接矩陣為布爾型DSM，其運算規則遵守布爾代數有關的算法，設構成產品元件集合為P={p1,p2,…,pi,…,pj,…,pn}，產品元件之間關系的集合為D={d1,d2,…,dm}，則有向圖Q=〈P,D〉是階數為n的鄰接矩陣A，其元素aij為

(4)

通過產品設計結構有向圖，對應得到其鄰接矩陣A={P,D}，有向圖與鄰接矩陣關系如表1所示。

表1 產品元件有向圖與鄰接矩陣

當設計結構矩陣中存在沖突元件時，定義n階方陣C=(cij)n×n，其中

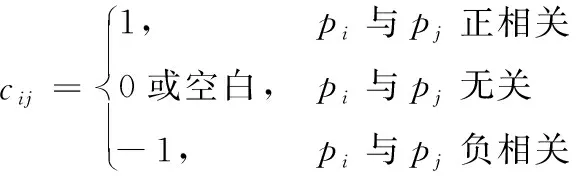
(5)

則稱矩陣C為該設計結構矩陣的沖突矩陣，且該設計結構矩陣的聚類矩陣R的定義式為

R=P1+P2+…+Pn+nC

(6)

式中：P為R的鄰接矩陣，n為沖突強化系數。

2.3 建立分支拓撲樹模型

對結構進行元件裝配的優化與創新時，要按照一定的約束進行分解，這屬于多學科離散性優化的問題，將設計結構矩陣與分支拓撲樹結構進行映射，將其轉化為分支拓撲樹圖論的分解結構以便于對最優方案進行評價與遴選，并劃分子模塊，分支拓撲樹與多種算法結合使用，使數據簡潔，冗余信息最小化。

分支拓撲樹圖：常用Graph=〈V,E〉表示，其中V表示配置元件節點集，E表示配置元件邊集。

分支拓撲樹子圖：若有兩個無向圖Graph′與Graph，存在V′?V且E′?E，則稱Graph′為Graph的子圖。

分割矢量：對于產品元件結構而言，通常用分支拓撲樹的“點”表示各個元件，且處于樹終端；用“邊”表示元件之間的連接關系，用二進制變量φi表示分支拓撲樹中的分割矢量，φ的定義式為

φ=(φ1，φ2，…，φE)

(7)

φi=0(edgeremoved)或1(edgeexists)

(8)

分支拓撲樹一般分為有根拓撲樹與無根拓撲樹，如圖2所示，其中無根拓撲樹不含信息流向方向，僅展示元件間相互關聯性，故本文采用有根拓撲樹進行研究，有根拓撲樹(n≥3)可產生ψ種分支拓撲樹子圖，如圖3所示，其中ψ定義式為

(9)

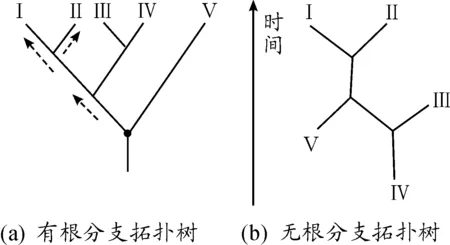
圖2 有根與無根分支拓撲樹

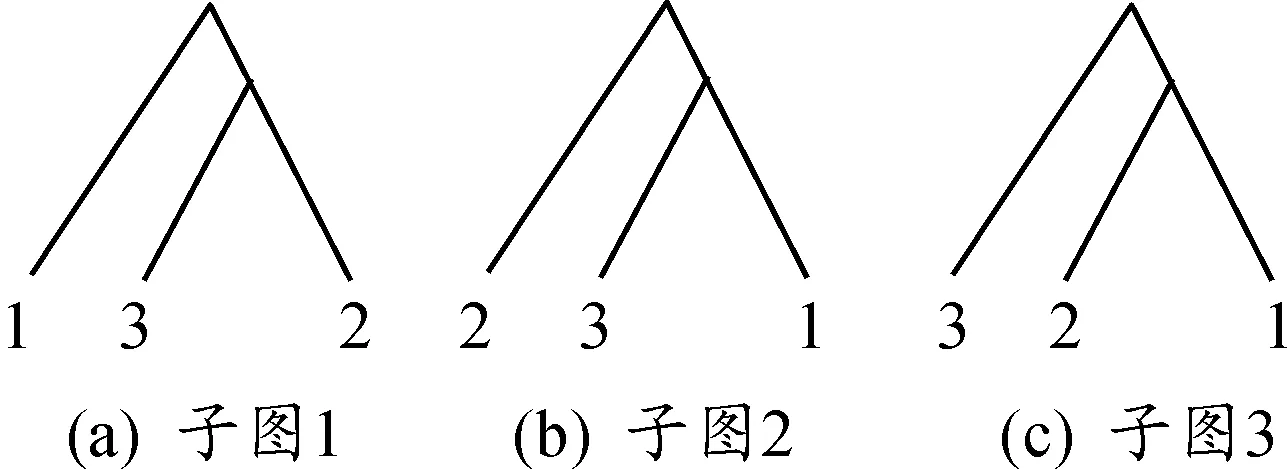
圖3 n=3的分支拓撲樹子圖

2.4 產品設計結構矩陣聚類評價分析

在產品設計結構矩陣進行模塊劃分時，要確保模塊內關聯程度大，模塊間沖突指數小，即遵循高內聚低沖突的聚類原則，根據該原則對多方案進行評價與遴選，得到最優方案。

沖突指數是指設計結構矩陣中模塊間的排斥程度，直接反映了模塊間的獨立性，本文利用沖突指數Obj作為評價模塊間排斥程度的重要指標，其定義式為

(10)

式中：Ci為聚類子模塊的矩陣大小；I0為聚類子模塊外設計要素個數總和；α與β為權值系數，可用來調整沖突指數的影響程度，這里取α=10,β=100。

內聚度是在單模塊內各組成部分間的關聯程度，關聯程度越大，表明模塊相對獨立性越強。目前，大多采用布爾型設計結構矩陣的產品模塊劃分指標對模塊內的關聯程度進行計算，對給出的N個設計結構矩陣聚類模塊S={s1,s2,…,sN}，Win的定義式為

(11)

(12)

(13)

在聚類模塊si中，設計結構矩陣的模塊化程度越高，對應于win(si)越小，說明該聚類模塊相對結構緊密，對于產品總體結構而言，win越小表明設計結構模塊化程度越高，反之，則說明模塊化程度越低。

由式(10)與式(11)可以得知，在多方案遴選中，沖突指數Obj與內聚度Win越小，表明在設計結構矩陣中的聚類效果越好，由此可作為方案評價與選擇的重要指標。

2.5 分支拓撲樹粒度層級分析

為進一步對最優方案進行子模塊劃分，以得到滿足需求的配置元件組合，將設計結構矩陣與分支拓撲樹進行映射，利用模塊指數MI(Modularity Index)確定最優集成元件子模塊，其定義式為

MI=I+Z

(14)

式中：I為子模塊外設計要素1的總和；Z為子模塊內設計要素0的總和。

分支拓撲樹粒度層級分析步驟如圖4所示，其中第一粒度層級包含兩個子模塊{C、D、E、F、A}和{B}，MI為10；第二粒度層級包含三個子模塊{C、D、E}、{F、A}和{B}，MI為6；第三粒度層級包含四個子模塊{C、D}、{E}、{F、A}和{B}，MI為10，第四粒度層級包含六個子模塊{C}、{D}、{E}、{F}、{A}和{B}，MI為14，在粒度層級分析中，取模塊化指數MI最小的為最優粒度層級，圖4中第二粒度層級的模塊化指數MI最小，故最優集成元件子模塊為{C、D、E}、{F、A}和{B}。

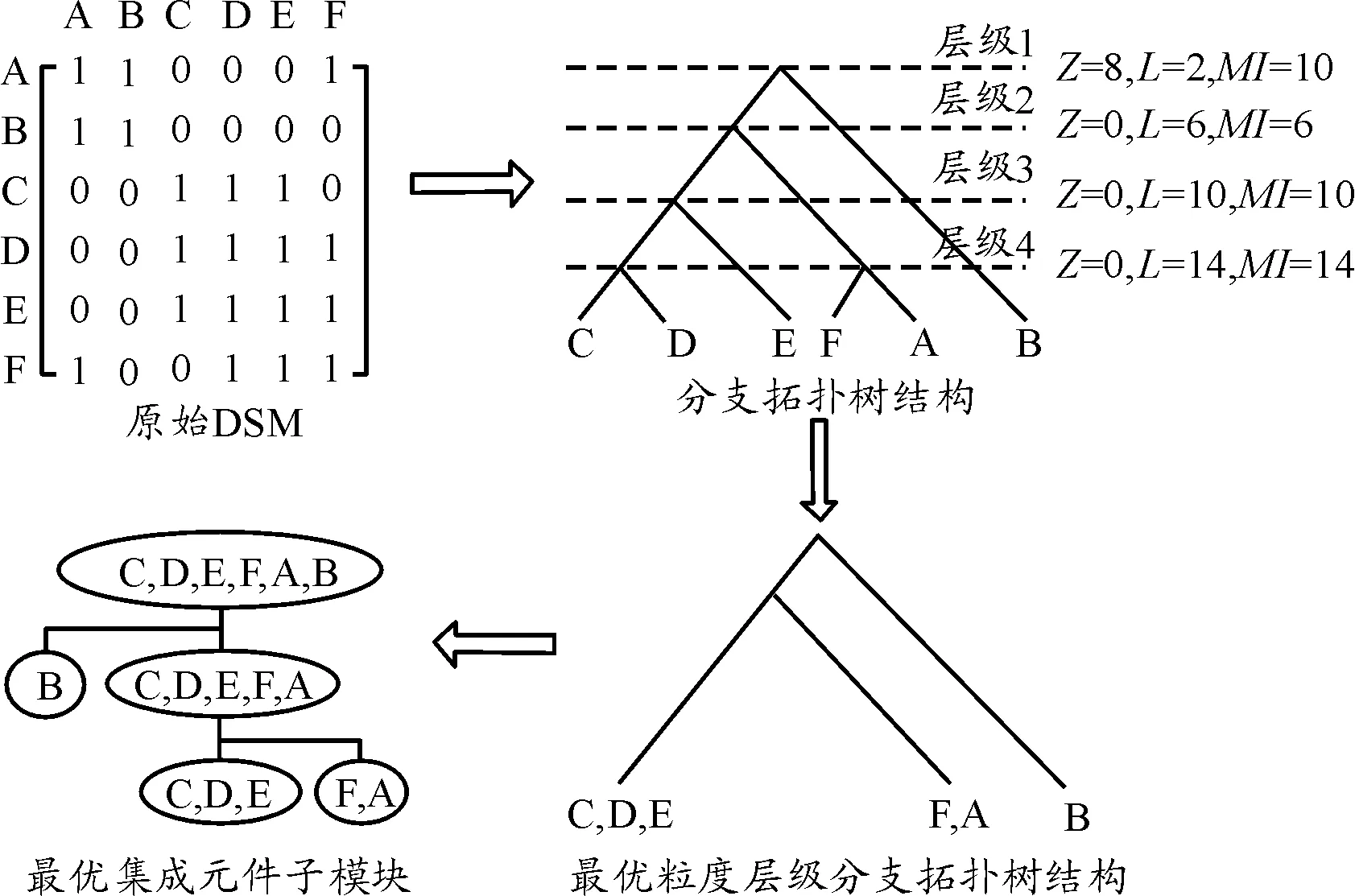
圖4 分支拓撲樹粒度層級分析步驟

3 案例

與履帶、輪式等成熟物理平臺的機器人相比，液壓四足機器人在機動、感知、承載、防護等方面尚有較大改善和提高空間，以美國波士頓大狗機器人為例，其縱向自由度位置貼近地面，對復雜地形適應性較好，但其髖部橫向自由度距離地面較遠，影響其靈活性。本案例以五款典型液壓四足機器人為設計原型，對腿部結構元件(如圖5所示)進行沖突分析，目標是創新新的腿部結構設計方案，使其更好的適應非結構化地形。

圖5 液壓四足機器人的腿部結構元件

五款液壓四足機器人的主要元件配置如表2所示。

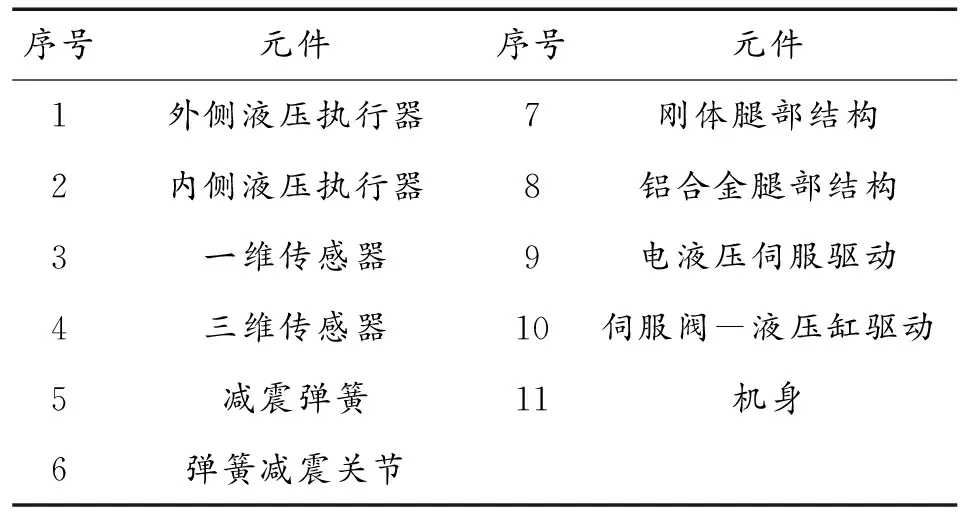
表2 液壓四足機器人元件

機器人腿部共11個主要元件，為簡明起見，配置元件間無任何聯系的0未標識，用DSM1、DSM2、DSM3、DSM4、DSM5分別構建設計結構矩陣，如下：

其中，負元素表示配置元件存在沖突互斥現象，即不可同時存在于同一液壓四足機器人中，建立液壓四足機器人元件沖突設計結構矩陣Q,如下：

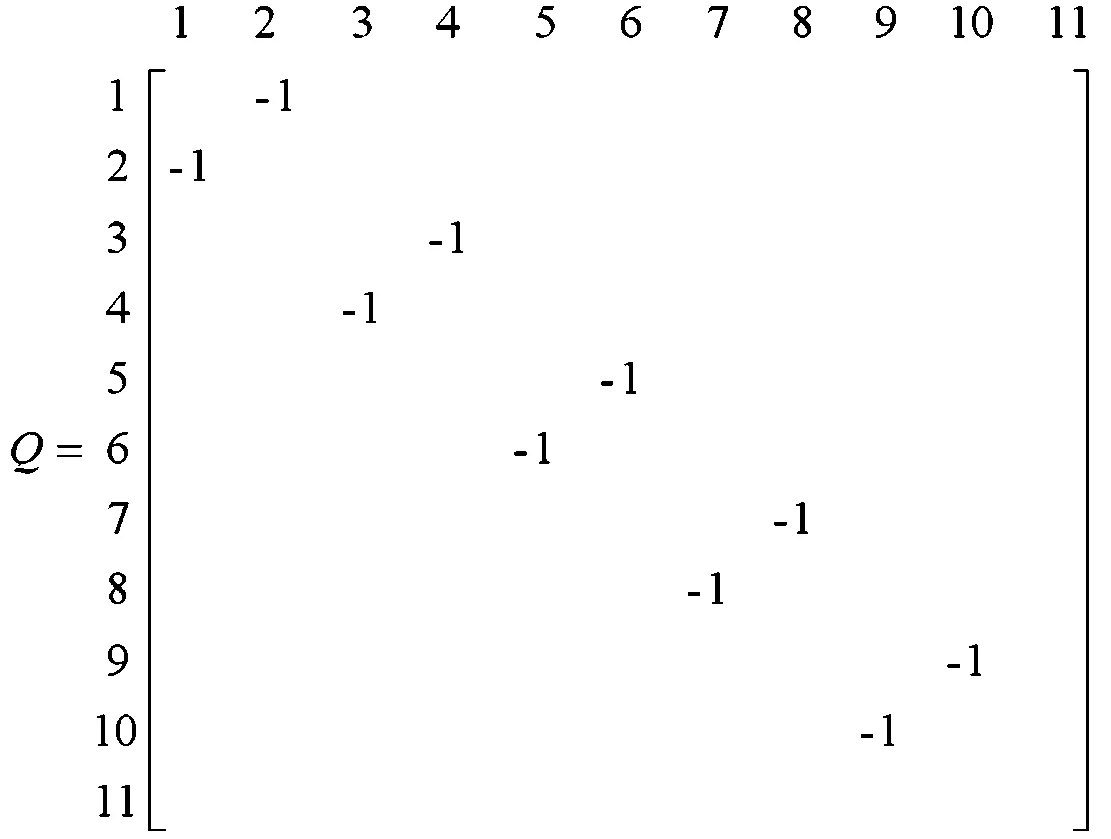
利用式(6)，將六個設計結構矩陣進行累加，同時加強負元素在聚類設計結構矩陣中的影響，避免單模塊間的互斥現象，得到最終的聚類設計結構矩陣DSM，如下：

通過分支拓撲樹對液壓四足機器人聚類設計結構矩陣進行分析，本案例共有11個元件，根據式(9)，可產生 6 547 290種分支拓撲樹子圖，選其中六款典型的六級分支拓撲樹子圖方案進行比較，如圖6所示，拓撲樹終端元件重新排列，利用式(10)，依次計算其聚類沖突指數，對這六種方案進行遴選。

其中方案1、方案4與方案5的聚類沖突指數較高，不滿足液壓四足機器人腿部元件設計，故應排除；對方案2、方案3與方案6分別構建設計結構矩陣，如圖7所示，(a)聚類方案2分為兩個子模塊x1(2，8，5，3，11，10)與x2(9，4，6，7，1)；(b)聚類方案3分為兩個子模塊x1(7，4，1，6，11，9)與x2(10，5，2，3，8)；(c)聚類方案6分為兩個子模塊x1(7，1，4，6，9)與x2(11，10，5，3，2，8)。

圖7 三種聚類方案

利用式(11)，分別對3種方案的子模塊內聚度進行計算，以方案2中子模塊x1(2，8，5，3，11，10)為例(參見圖8)，計算該子模塊內聚度

其他模塊的內聚度計算以此類推，得到方案2的內聚度

同理計算方案3與方案6的內聚度，結果見表3，從表3可以得出聚類方案2的內聚度最小，其聚類子模塊間的結構緊密，故為最優聚類方案。

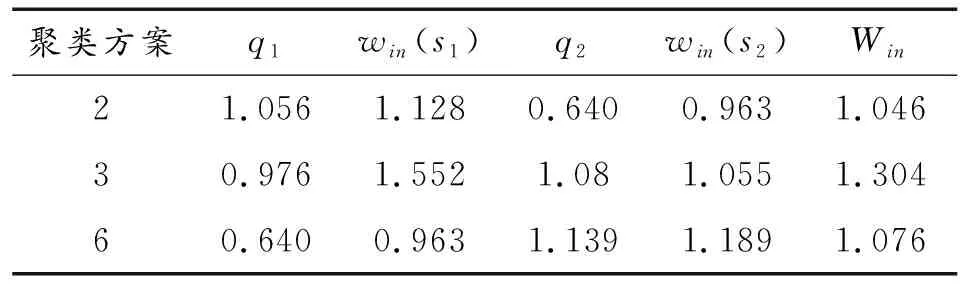
表3 聚類方案的內聚度指數

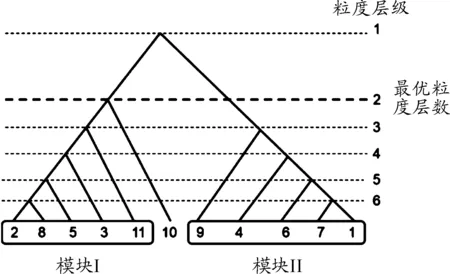
圖8 方案2分支拓撲樹粒度層級

為進一步確定方案2的最優集成元件子模塊，利用式(14)確定每一層級的模塊化指數，結果如表4所示，確定最優粒度層級。

表4 粒度層級模塊化指數

第三層級中，分解的分支圖產生兩個子模塊，模塊Ⅰ為{2，8，5，3}由“內側液壓執行器”、“鋁合金腿部結構”、“減震彈簧”、“一維傳感器”構成；模塊Ⅱ為{4，6，7，1}由“三維傳感器”、“彈簧減震關節”、“剛體腿部結構”與“外側液壓執行器”構成，模塊Ⅰ與模塊Ⅱ均缺少“機身”這一關鍵組件，無法組成完整的機器人腿部結構，第四層級、第五層級與第六層級均存在相同的問題，故均應排除。與第一層級相比，第二層級的模塊化指數較小，為最優粒度層級，其由兩個子模塊組成，將第二層級的模塊Ⅰ與模塊Ⅱ進行比較，模塊Ⅰ為{2，8，5，3，11}由“內側液壓執行器”、“鋁合金腿部結構”、“減震彈簧”、“一維傳感器”與“機身”構成，機器人腿部結構完整，在非結構化地形中運動性能更好，根據第二層級模塊Ⅰ中的元件配置生成本案例的創新方案，如圖9所示，為4自由度配置方案，配置3條液壓缸使得系統的總重量容易控制，臀部側展關節(Hip a/a)、臀部擺臂關節(Hip f/e)，膝關節(Knee f/e)為主動運動關節，由3條液壓缸推動關節實現鉸接運動；足部為被動自由度，安裝彈簧-阻尼，實現系統的減震作用，該方案的優點在于結構清晰、合理，以最少的自由度，實現了四足移動的仿生學原理，更好的滿足了非結構化地形中的多種需求。

圖9 液壓四足機器人腿部創新方案

4 結論

采用設計結構矩陣與分支拓撲樹結構相結合的方法，對存在沖突的元件進行聚類模塊化，對于多種方案綜合考慮沖突指數與內聚度，并將其作為方案遴選的評價依據，同時利用分支拓撲樹結構確定最優粒度層級，對最優方案進行再次子模塊劃分，優化產品配置。通過液壓四足機器人腿部結構的案例分析，說明了基于設計結構矩陣與分支拓撲樹結構的產品模塊劃分方法和有關的評價指標的適用性，可以改善產品設計，創新產品方案。