基于真值發現的加油站車輛號牌缺損數據填充方法

彭新亮 程 力 王 軼 馬 博 趙 凡 周 喜*

1(中國科學院新疆理化技術研究所 新疆 烏魯木齊 830011)2(中國科學院大學 北京 100049)3(新疆理化技術研究所新疆民族語音語言信息處理實驗室 新疆 烏魯木齊 830011)

0 引 言

隨著自動化數據采集技術的發展,加油站車輛加油數據的采集工作正在逐漸由人工采集轉向物聯網設備自動采集。由于數據采集設備的車牌識別精度不足、環境影響、網絡不穩定等因素的影響，同一輛汽車在不同加油站終端數據系統中所采集到的車牌號碼也有可能不同。并且，從這些設備匯總得到的數據中車牌號碼存在大量丟失和錯誤(以下簡稱缺損)情況。某地區收集的車輛加油數據中，缺損數據約占總數據的20%以上。由于未采用有效的方法對此部分數據進行處理，嚴重影響了后續對這些數據的分析工作，不利于數據融合的開展。因此，針對這種多數據源離散型分類數據的缺損值填充問題的研究，對于提高原始數據的可用性和融合數據的正確性都至關重要。

在融合互聯網多源數據時，由于不同數據源自身數據不完整的原因，導致相同數據在融合時產生沖突，無法確定真值的問題。Yin等[1]首次將此問題定義為真值發現，并提出了TruthFinder算法解決此問題。鑒于多源數據的特殊性和數據質量的重要性，本文提出了一種基于真值發現的缺損數據填充方法。該方法將經過預處理的數據通過改進的Truth Finder迭代計算真值，再按照一定的策略對缺損數據進行填充，有效地解決了多數據源離散型分類數據的缺損值填充的問題。

1 相關工作

對于缺損數據的處理在數據的預處理階段十分常見。就目前而言，在數據挖掘和機器學習領域對于缺損值的處理方式主要分為兩類，直接刪除相應缺失數據所在數據行和算法填充[2]。又根據填充數據的產生規則，可將數據填充分為基于數據集自身統計特征的填充和基于機器學習模型的預測值填充兩類[2]。

直接刪去缺損值所在的數據行的方法，可以非常簡單地使得原始數據成為完整的數據集。在缺損數據所占比重較小的時候采用這種方法是很有效的。然而，操作簡單意味著其局限性也十分突出。因為直接刪去了原始數據的若干記錄會造成原始數據的缺失，一些隱藏在數據中的信息同時也會被遺棄，這將直接影響下一步的數據分析結果的有效性。甚至在缺損數據量較大時，使用這種方法會直接導致原始數據偏離正常分布，給出錯誤的數據挖掘結果。

在統計學領域，一些學者提出了用統一值、平均值等一些基本統計量來對缺損值進行直接替換，使得原始數據形成完備數據集。文獻[3]介紹了使用方差校正的方法，對缺損數據進行插補。文獻[4]介紹了使用最大期望算法(Expectation Maximization Algorithm, EM)和貝葉斯網絡(Bayesian network)的丟失數據填充算法。該算法利用Naive Bayesian模型估計出EM算法的初始值，然后結合這兩種模型迭代確定更新器，同時對缺損值進行填充。這些方法的優點是簡單快速，對于數據維度不大的數據集而言是一種有效的處理手段。但是在缺損數據所占比重較大或者數據較為復雜時，這種方法很可能會丟棄原始數據中的大量隱藏信息，甚至影響原始數據整體的分布情況，直接影響數據的可用性。

更為普遍的方法是對缺損值進行預測填充，尋找缺損值的最近似值來進行替換。研究者們提出了大量基于統計分析、機器學習的模型和算法。文獻[5]將數據分為決策屬性和條件屬性，利用支持向量機來預測條件屬性的值，從而填充缺失數據。除此之外，也有采用K最近鄰算法[6-8]、信息增益[9]、人工神經網絡[10-12]等算法對缺損數據項進行預測，找出最有可能的數值來進行填充。

這些方法在處理缺失數據方面各有優勢，某些算法模型在處理連續型數值數據時會取得較好的效果。而某些算法更適用于離散型數值數據。但是對于加油站車輛數據這種離散型分類數據而言，目前仍未找到有效的處理方法，一種可行的方法是按照不同加油站根據車輛加油的頻率，按照少數服從多數的方式，使用投票(Voting)的策略估計缺失數據[13]。本文提出了使用改進過的用于真值發現的TruthFinder算法將處理過的原始數據輸入到算法模型中，通過迭代計算的方式求得數據的真實值，然后按照一定策略對算法將得到的真值填充回原始數據中，以此解決加油站車輛號牌缺失數據的填充問題。通過在真實加油站數據集的實驗結果證明，該方法相較于傳統的Voting算法有23%的正確率提升，很大程度上提高了加油站數據的可用性。

2 缺損值填充框架

2.1 問題的產生背景

數據質量問題作為制約數據可用性的關鍵問題，長久以來深受研究者的重視。如何對原始數據進行清洗，提高其可用性，是大家關注的重點。文獻[14]針對數據質量問題提出了一個可以動態配置規則的數據清洗框架，如圖1所示。

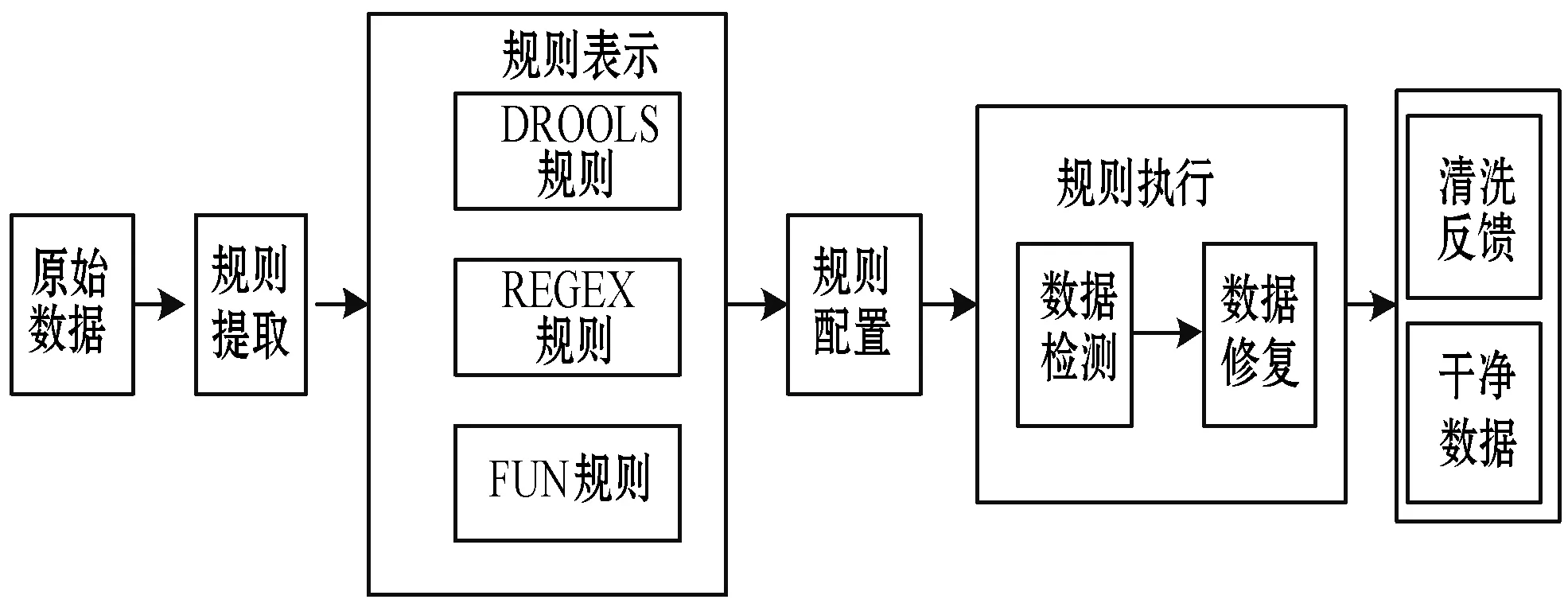
圖1 動態配置規則的數據清洗流程

在對加油站數據進行預處理階段，主要任務是對數據文件某些字段中的錯誤、缺失和不一致問題進行修正。如圖1所示，該框架使用了三種可動態配置的規則(DRDDLS、REGEX、FUNCTION)以及規則間的邏輯運算，可以對臟數據進行保留、丟棄、回填三種修復操作。但是在實際應用于真實數據時發現，數據修復階段往往由于大量數據的丟失，而無法為其配置合適的規則，從而導致無法有效地對數據開展清洗工作，使得最終的清洗結果無法達到要求。因此本文針對此問題提出了解決方案。

2.2 問題的定義及分析

在加油站車輛數據中，每條數據包含車輛的駕駛員信息、加油站信息、車輛的車牌號碼等內容。

由于一些原因，數據中存在大量無法使用傳統圖像再識別等方式修復的數據，制約了數據的可用性。因此，如何使用算法將丟失的號牌盡可能修復出來，從而提高數據的可用性將十分有意義。

如圖2所示，車主在加油站A與加油站B等多個加油站進行過加油。由于加油站設備的原因，導致不同的加油站數據庫中存放車輛號牌產生區別，至少有一個車牌識別結果是錯誤的。在各加油站數據需要融合處理時，需要對其真值做出判斷。此外，若存在此車主在加油站C的加油記錄且此記錄中車牌號碼識別失敗產生缺失數據時，又涉及到如何填充此缺損值的問題。因此，為了保證加油站數據的可用性，需要對這樣的數據進行填充處理。

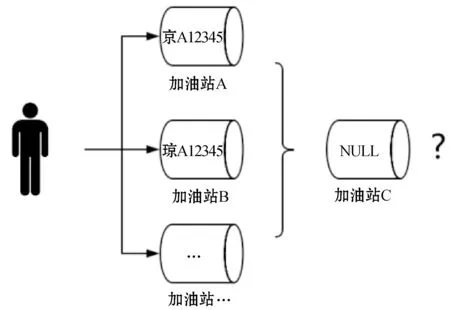
圖2 加油站數據真值問題

在討論缺損值填充問題之前，基于常識和對數據的觀察，提出一些基本的假設，以便于下述問題的處理：

假設一：各個數據源之間不存在聯系，所提供的數據相互獨立，這個條件在加油站數據中顯然成立，不同的加油站之間并沒有任何數據間的聯系。

假設二：在某個區域內的一段時間里，一個普通用戶(以用戶身份證號碼為區分)不會頻繁更換車輛加油。即一個用戶不會每次都駕駛不同的車輛進行加油，顯然，大多數人是滿足該假設的。這樣車輛就與用戶關聯起來了。

假設三：車輛加油存在一定的連續性，某輛車大概率會在某地區內頻繁加油，而小概率不在本地區加油。

2.3 符號及其含義

表1給出了真值發現問題中的一些基本概念及其描述。

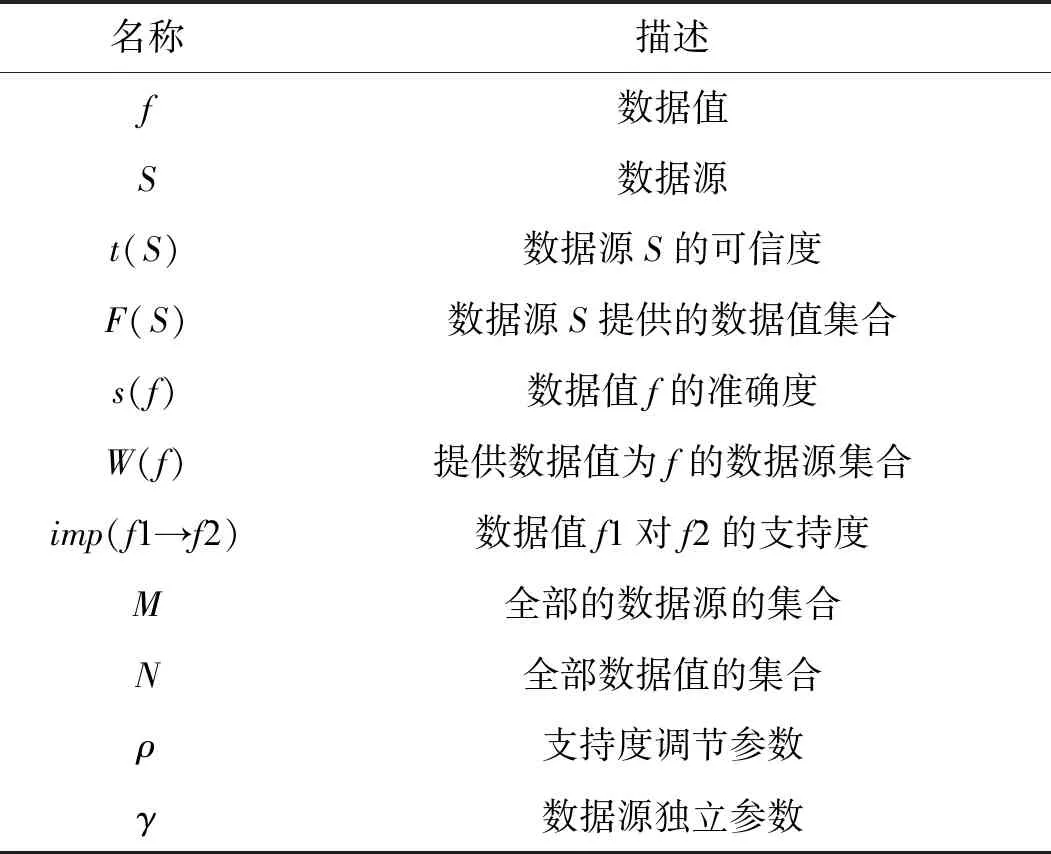
表1 規則、符號的意義

2.4 TruthFinder算法

在多源數據融合領域，不同數據源對數據的表示方式、格式等不同，在對多源數據進行融合時會遇到無法判斷來自哪個數據源的值正確或者以哪個數據源的值為準的問題[15]。

為解決此問題，TruthFinder算法將各個數據源看作一張圖上的節點，定義出了數據源的可信度和數據值的準確度兩個變量描述這個圖，使用迭代計算的思路分別計算數據值的準確度和數據值的可信度，直至收斂。

算法開始時，統一設定所有數據源的初始可信度為t(s)，假設一個實體真值數據只存在一種數據值f,則某數據源的數據值錯誤可能性為1-t(s)，故在全部數據源的基礎上可計算得到數據值的準確度為：

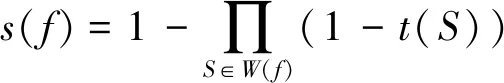
(1)

在求得各個數據值的準確度之后，算法即可根據簡單的幾何概率模型求得某一數據源的可信度為該數據源所表示的所有數據準確度之和與該數據源所描述數據值的個數|F(S)|的比值。即數據源S的可信度為：

(2)

以上是簡單模型中求解數據源可信度和數據值準確度的過程。由于一個現實實體真值在多源情況下不可能只有一個數據值描述值，因此，不同數據源中會有對同一數據的描述，往往這些描述是相互關聯的。將數據值f1對數據值f2的關聯記作imp(f1→f2)。故調整后的數據值準確度如下，其中ρ是調節參數：

(3)

原算法考慮到不同數據源之間的并非完全獨立，在處理最終結果時加入了數據源獨立參數γ調節最終結果:

s*(f)=1-e-γ·s(f)

(4)

由式(2)和式(4)即可迭代計算數據源的可信度和數據值的準確度，直至計算結果不再變化為止，所得到的準確度最高的數據值即為所求的真值。

2.5 基于真值發現的缺損值填充方法

本文所用方法整體框架如圖3所示。

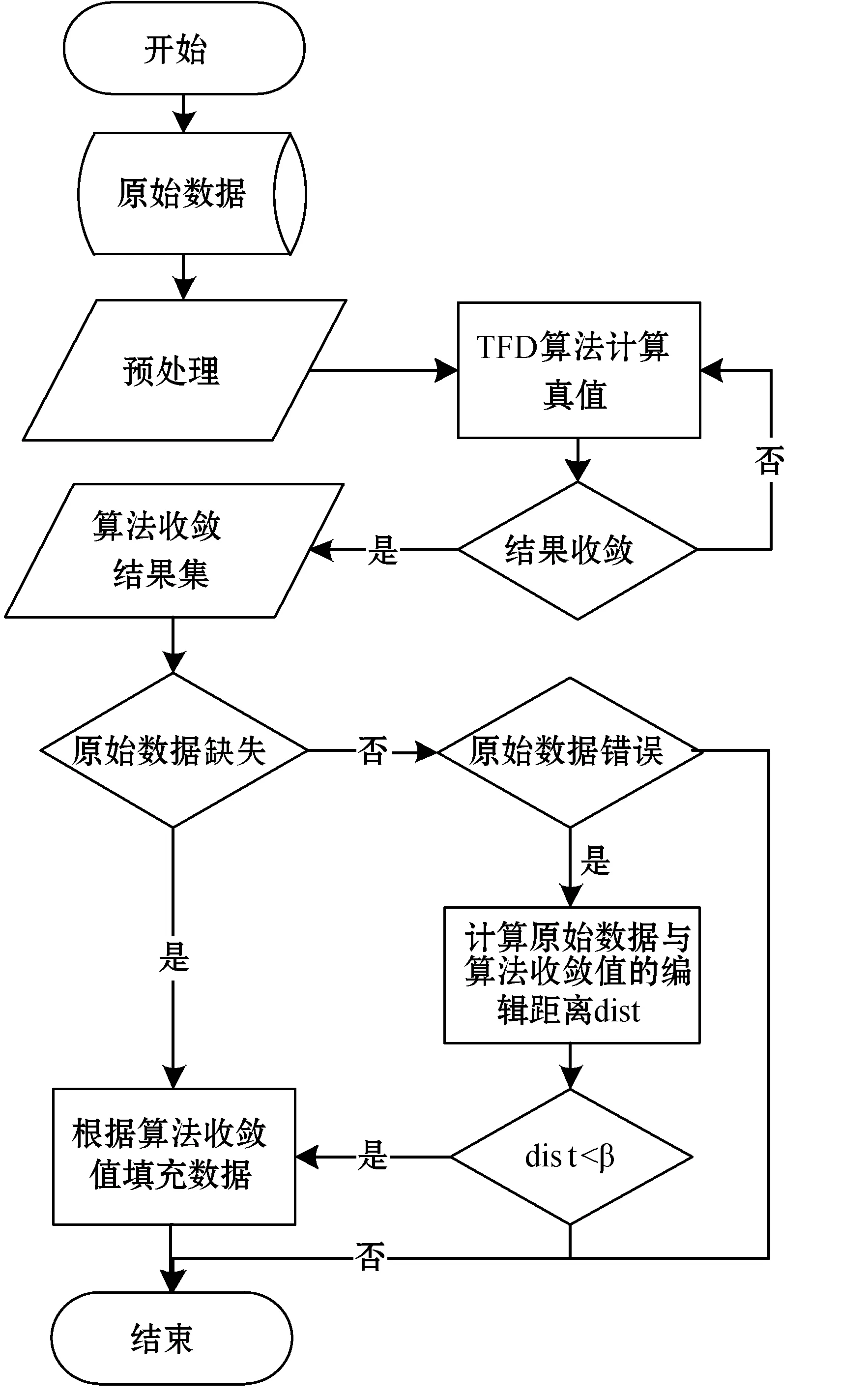
圖3 基于TFD(Truth Filling Declare)算法的 缺損值填充計算框架

在傳統的真值發現算法中，數據值之間的支持度imp(f1→f2)定義比較模糊，大部分直接將數據看作普通文本，使用兩個數據值的余弦相似度用于計算。由于處理數據的類型不同，這樣的做法在加油站車輛數據這種短文本數據中顯然是不合理的。例如，用戶A在f1加油站加油時識別的車輛號牌為“京A12345”,在加油站f2加油時識別的車輛號牌為“津A12345”。這其中顯然有一個加油站的數據是錯誤的，此時若按照傳統的相似度作為支持度的計算，則:

imp(f1→f2)=cosine(f1,f2)=

在上例中，根據詞頻可以將f1的向量表示為(1,0,1,1,1,1,1,1)，f2的向量可以表示為(0,1,1,1,1,1,1,1)。可以計算得到二者的余弦相似度為0.857，顯然這樣的相似度表明這兩個數據之間存在較高的支撐關系。反映到實際的計算中就會導致異常高的支持度，這樣在進行迭代計算的過程中，某些實際錯誤的數據會因為其他數據的較高支持，也計算得到較高的準確度，從而影響最終進行數據填充的結果。為了解決加油站車牌數據中使用文本相似度所帶來的問題，本文提出采用0-1相似度來計算數據之間的支持度，其計算公式如下：

這樣可以使得在短文本真值算法處理時獲得更加準確的計算結果。

2.6 數據填充過程

如圖3所示，在原始數據預處理階段需要從數據庫中抽取數據，由于原始數據在維度、格式上與TFD算法要求的輸入存在差異，需要進行相應的格式轉換。格式轉換完成后，會對原始數據進行適當刪減，去除那些不滿足算法假設的數據。例如在整個數據集中只進行過一次加油或者某輛車每次加油都是不同的車主駕駛，這些數據將無法被算法框架所計算。另外，在實際情況中，單個數據源內部由于一些原因，其多次提供的數據值可能也存在偏差。因此需要統一單一數據源的描述值。

通過對原始數據的預處理，得到相應的實驗數據集，實驗數據集將直接作為TFD算法的輸入。之后將采用迭代計算的方式計算真值，根據輸出結果即可知道不同數據的真實情況。計算過程的偽代碼如下：

輸入：經過處理的各個加油站不同用戶的加油數據{F(S)}S,∈M。

輸出：各個用戶所駕駛車輛的真實車牌號碼數據值{s(f)},f∈N和各個加油站數據可信度{t(S)},S∈M。

(1) Initialization, 初始化各個數據源的可信度{t(S)},S∈M;

(2) Repeat:

(3) Fori< 1 to│M│ do

//循環計算每個數據源

(4) 根據式(3)與式(5)計算數據值的準確度s(f);

(5) End for

(6) 根據所求得的準確度和式(2)更新此輪迭代計算 的數據源可信度t(S)；

(7) Until計算結果收斂;

(8) Return準確度最高的數據值s(f),f∈N作為真實值，數據源的可信度{t(S)},S∈M。

經過上述迭代計算之后，即可求出在此模型下某個用戶駕駛車輛車牌號碼的真實值。算法的最后一步中，真實值將被用于回填數據庫。此過程分為兩類，對于缺失的數據，將直接填充TFD算法求得的數據值；對于錯誤的數據，由于實際數據中存在一個用戶會駕駛多輛機動車加油的情況，因此采用比較算法真實值與實際值編輯距離的方式進行填充。編輯距離Levenshtein distance[16]是一種常用的比較文本相似度的算法，設兩個字符串為a、b。其長度分別為i、j，則兩者編輯距離計算方法如下：

(7)

若兩者編輯距離小于某一閾值β，則表明原始數據中的錯誤值可能是由算法真實值丟失數據產生，應該進行替換。否則二者應該不是同一數據，不應該進行替換。根據對加油站數據的觀察，發現數據錯誤字符個數為1～2個，因此實驗中相似度閾值β取3。

至此，算法完成了對所有數據的缺損值填充過程，依此方法可以得到可用性提高的新數據集。

3 實驗與結果

3.1 實驗配置

為了驗證上文中提出的缺損值填充算法的有效性，本次實驗使用了真實環境中加油站車輛加油的數據,抽取某一區域的部分數據形成實驗數據集。實驗機器系統為Windows7 64位，CPU型號為Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz，內存8 GB，全部代碼使用java語言實現，jdk版本為1.8。數據存儲使用Oracle 11g。

3.2 加油數據集

數據來源于新疆維吾爾自治區烏魯木齊市的真實加油站加油數據，該數據集從原始數據庫中，抽取市區了31個加油站2017年1月至2017年11月的加油數據總計702 508條。為了保證實驗的準確性，去除了數據中部分無效數據，例如整個時間段內加油次數為1次、整個時間段內所有車牌數據均為錯誤等無法被填充框架處理的數據。經過數據篩選和格式轉換等步驟，最終形成了總共659 155條記錄的實驗數據集。其中完全缺失車牌號字段的數據128 354條，數據缺失率為24.18%。參與運算的完整數據(包含錯誤數據23 851條)530 801條。其中每條記錄主要包括唯一性標識、加油人員身份證號碼、加油站編號、車牌號等信息。以某一用戶為例，數據集中了不同數據源對其描述數據以及真實情況下加油車輛的電子照片，如表2所示，其中“#”號表示數據缺失，(敏感部分以*代替)。

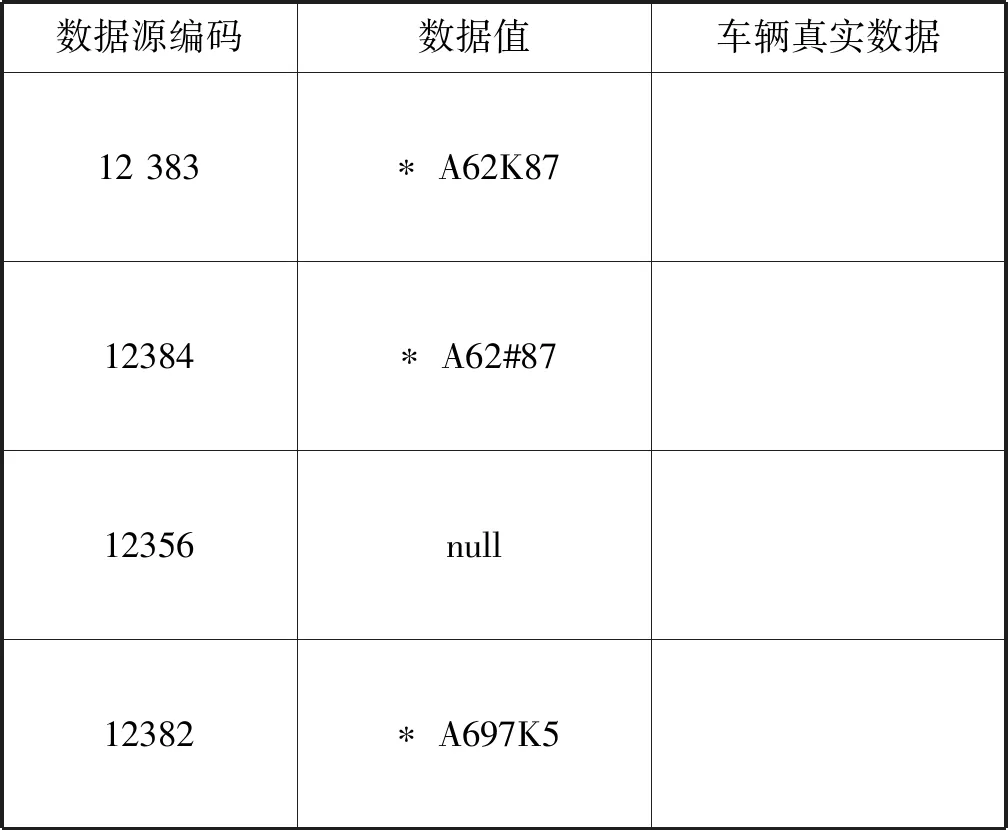
表2 加油數據集部分數據

本文中采用真值發現常用的正確率[1-13]來衡量最終結果準確性。其計算方式如下：

式中：TP表示算法計算的結果中為真的數據值個數，P表示算法返回的結果集對應取樣數據的數量。為更加真實地計算算法的準確性，本文采用真值發現通用的Gold standards[1]準則進行評價，測試數據的具體選擇方法為：隨機挑選實驗數據集中的數據，采用人工的方式在后臺數據庫中尋找此數據未缺失的真實值，真值以數據庫中記錄的圖片數據為準。

本次實驗共分為兩個部分，第一部分比較TruthFinder算法中的兩個參數ρ和γ對于實驗結果的影響，并選擇合適的參數進行第二部分實驗。第二部分實驗中比較Voting算法、原始TruthFinder算法與改進后的TFD算法在實驗性能對比及分析。

3.3 參數對結果的影響

為了更好地建模數據源之間的關系，原算法加入了兩個參數ρ和γ。其中ρ表示最終結果中本數據源和其他相關數據源對結果的貢獻比例，一般取0.5；γ是數據源的獨立性參數，為了防止數據源不獨立時迭代結果異常的現象產生。不同參數對實驗結果的影響如圖4所示。

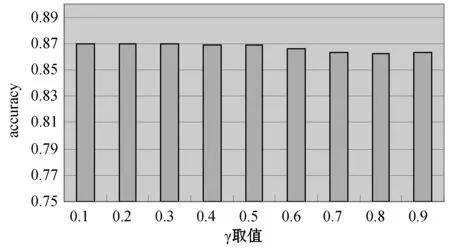
圖4 不同γ取值對正確率的影響

上述實驗中，固定算法支持度參數ρ為0.5，即數據的準確度計算同時考慮當前數據源結果與其他數據源對本數據的描述，這是大多數真值發現算法所采取的策略。得到參數γ在不同數值下算法最終正確率的情況。參數γ在算法中描述的是不同數據源之間的獨立性，即一個數據源的數據是否與其他數據源的數據有關。由實驗結果可知，隨著γ在參數范圍0～1內變化，最終算法正確率雖然有少許波動，但整體來看變化不大。

3.4 實驗性能對比及分析

本小節比較了三種算法在實驗數據集上的效果。具體包括作為對比的Voting投票算法[17]，即按照少數服從多數的方式選擇真值、基于原始未修改的TruthFinder填充算法和本文提出的改進原TruthFinder算法中關于數據值支持度的TFD算法。本實驗中所選取的參數均以上述實驗中獲得最優結果為準：ρ=0.5，γ=0.1。實驗結果如表3所示。

表3 不同算法的正確率對比

由實驗結果可以看出：基于TFD的缺損值填充方法取得了最高的結果正確率。相較于TruthFinder算法和基于投票的Voting算法有了7%和23%的正確率提高。Voting算法作為處理類似問題的通用計算方法，采用少數服從多數的經典處理策略，并未考慮到不同數據源本身的特點，計算模型過于簡單，僅考慮某一數據值的出現次數。雖然在處理離散型多源數據填充問題上有一定的使用價值，但是正確率不高。

基于TFD的填充算法在TruthFinder的基礎上改進了其支持度的計算規則，最終在正確率上有一定的提高，說明在加油站數據中，相較于余弦相似度這種在文本相關性方面較為優勢的算法，離散的0-1相似度更具有效性。TFD算法將車牌之間的支持度離散化處理，因此在實際實驗中獲得了比TruthFinder算法更好的效果。

如圖5所示，算法在最開始的三輪迭代中正確率有明顯變化，且變化率不斷降低，之后正確率穩定，表明迭代已收斂。而且，即使是在首輪迭代中，算法的正確率依然有0.866，可見，在一輪迭代后其結果已有一定的可用性。基于TFD的缺損值填充算法在處理數據量較大的數據集時，也可以在較短的時間內得到令人滿意的結果。

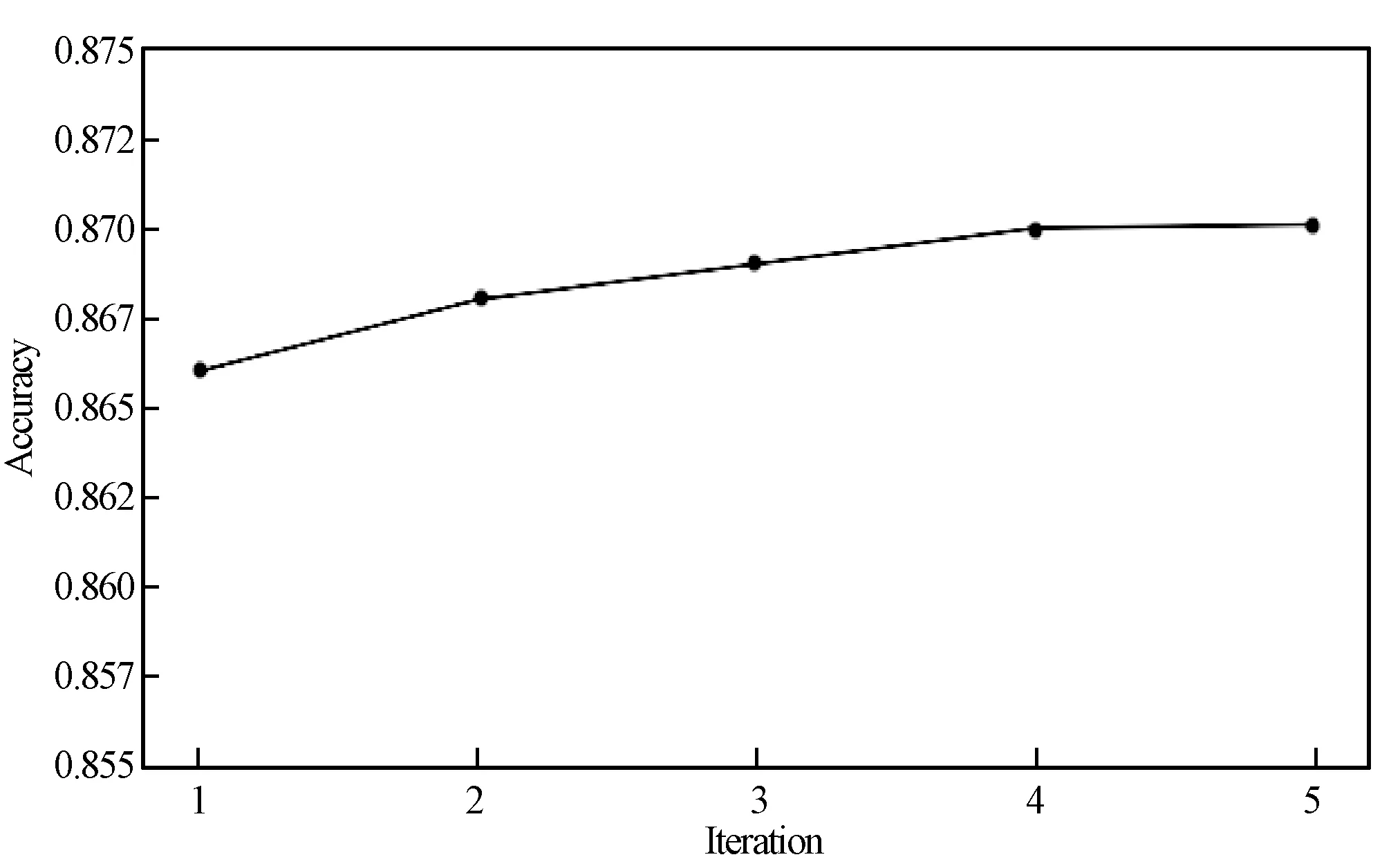
圖5 算法正確率隨迭代次數的變化

4 結 語

針對于多源離散型分類數據缺損值填充問題，本文提出了一種基于改進的TFD算法進行填充的思路。該方法使用真值發現，迭代計算各個數據源的可信度和數據值的準確度，使用改進的二值相似度解決了數據之間支持度的計算問題，以最終迭代收斂時的計算結果作為缺損值填充的備選值。最后通過在實際數據集上的實驗驗證了這種方法的有效性。本文為解決此類問題提供了一種全新的解決思路。但是真值發現算法發展至今已有大量的研究進展[18-20]，本文所使用的算法只是其中較為簡單易于理解的一種。由于采用迭代計算的方式，其時間效率不高。其次，由于算法的局限性[21]，僅能處理單真值的問題。在后期對填充結果分析的過程中，發現小部分數據存在多真值的現象，導致算法填充結果不準確。因此，后續工作中將對真值發現問題進行更深入的研究，考慮采用不同的運算模型，提高在實際數據上的準確度和時間效率。