電路板在溫變載荷作用下的響應特性分析

李 政 ，史興華 ，王海東 ，蔣 剛

（1.西安電子科技大學 機電工程學院，陜西 西安710071；2.上海航天精密機械研究所 環境試驗檢測部，上海201600）

0 引言

隨著航天技術的迅猛發展，彈載電子設備的工作環境愈加嚴酷，確保和提高電子器件在極端工作環境下的工作性能，成為實現導彈在復雜環境下整體高穩定性和可靠性的關鍵。在實際服役過程中，電子器件會經歷振動、沖擊、熱真空以及溫度交變等運行環境，尤其是在溫度載荷條件下電子器件不同材料間熱膨脹系數差異會引起器件產生應力變形，造成焊點連接處產生裂紋，界面結構出現損傷，導致界面接觸電阻和熱阻增加，電信號傳遞受阻，甚至機械支撐崩塌，電子器件失效，電子設備壽命和可靠性受到嚴重影響。因此，分析研究電子器件內部熱量傳遞以及應力應變響應特性和機理，并且預測在熱環境下的電子元器件的疲勞壽命，有著現實的工程意義。

國內外學者對于不同熱環境下的電子封裝器件的響應規律和疲勞壽命做了大量研究。Chow等人[1]采用電子封裝結構1/8模型對不同大小的芯片進行熱循環仿真，研究表明通過控制封裝尺寸可以有效地提高無鉛焊點的疲勞壽命，并且最外側的焊點最容易失效。Wu等人[2]討論了焊點高度、焊點數量、回流焊溫度等參數對焊點疲勞壽命的影響，并對焊點蠕變和塑性特性進行有限元仿真，最終利用Coffin—Manson模型求出其疲勞壽命。Singh等人[3]將超薄玻璃球柵陣列（BGA）封裝放置在-40℃～+125℃進行熱循環和跌落測試的可靠性實驗，應用Engelmaier本構模型進行壽命預測，得出高壽命樣品均超過5000個熱循環的結論。李懷成等人[4]對塑料球柵陣列（PBGA）電子封裝結構中焊點采用Engelmaier的應變模型，將仿真分析和實驗結果對比預測出焊點在熱循環載荷下的疲勞壽命。劉艷鋒等人[5]根據當前預測焊點疲勞壽命和溫度應力復雜性的現狀，研究建立出簡單易行的三維有限元仿真模型，通過實驗標定參數，更為簡單地預測焊點熱疲勞壽命。徐夢凡和張帥等人[6]對直徑分別為0.8 mm、0.84 mm和0.88 mm的PBGA器件在熱循環載荷下的可靠性進行研究，應用Coffin-Manson模型來預測三種不同直徑的PBGA焊點的疲勞壽命，為工業中的電子封裝設計提供理論依據。王祥林等人[7]建立了含隨機孔洞焊點的熱疲勞壽命預測方法，即通過一種全新的多項式響應面的方法建立出焊點隨機空洞參數與應變能密度增量之間的關系，進而根據Darveaux壽命模型推導出含有隨機空洞的焊點的壽命預測模型。

針對板級電路在服役條件下不可避免地會經歷復雜環境，其中溫度交變載荷會導致電路板上封裝器件內溫度分布不均勻，并產生由于各組件熱膨脹系數差異而出現的變形及應力集中問題。本文以板級電路為研究對象，基于熱—結構耦合分析方法建立有限元模型，分析了該結構的溫度場變化規律及應力應變響應特性。

1 有限元模型的建立

考慮到電路板三維模型不具有對稱性，不能采用部分代替整體的方法進行有限元分析，故建立整板模型來進行有限元分析。電路板上主要有印制電路板、接插件、插座、溫濕度傳感器、穩壓芯片、晶振、按鍵、四方扁平封裝和小外形封裝等元器件，對于電路板上除四方扁平封裝和小外形封裝等不具有封裝焊點的元器件，采取等效質量塊的方法以原尺寸按照綁定的方式固定在印制電路板上[8]。

本文研究對象中四方扁平封裝和小外形封裝中的焊點材料為Sn63Pb37，焊點看作彈性模量隨溫度變化的非線性材料，并且采用Anand粘塑性統一本構方程來描述焊點熱力學特性。除焊點外，電路板中其他組成結構可看作是性能與溫度無關的線性材料[9]。其中PCB板的材料為FR-4，密度為1 500 kg/m3，彈性模量為17 200 MPa，泊松比為0.28，熱膨脹系數為15.7×10-6，導熱系數為10.5 W/（m·k），比熱容為1 136 J/（kg·k）。管腳的材料為Cu，密度為8 170 kg/m3，彈性模量為15 860 MPa，泊松比為0.30，熱膨脹系數為16.6×10-6，導熱系數為0.956 W/（m·k），比熱容為0.092 J/（kg·k）。基板的材料為環氧樹脂，密度為1 280 kg/m3，彈性模量為13 000 MPa，泊松比為0.25，熱膨脹系數為15×10-6，導熱系數為0.20 W/（m·k），比熱容為1.511 J/（kg·k）。焊點的材料為Sn37Pb63，密度為 8 420 kg/m3，泊松比為 0.35，熱膨脹系數為21×10-6，導熱系數為50 W/（m·k），比熱容為142 J/（kg·k）。

由于電路板的薄弱部位為四方扁平封裝和小外形封裝焊接處，故細化關鍵結構上的網格尺寸和數目，最終劃分共有224 674個節點，34 998個單元，整體單元的質量因子平均為0.85。電路板有限元模型網格劃分示如圖1所示。

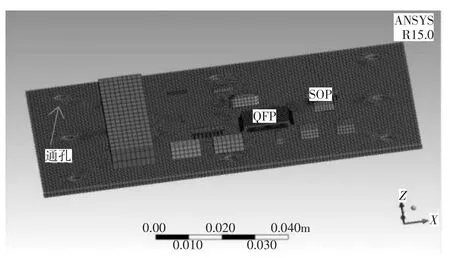
圖1 電路板有限元模型網格劃分

2 溫變載荷條件下電路板響應分析

2.1 電路板溫度場分布

在有限元分析中對電路板三維模型施加五個溫變循環周期的熱載荷，選定零應力下的環境溫度為20℃，并且由于電路板在實際工作中被放置于箱體等結構內，箱體內空氣流動速度較低，電路板上各封裝器件與周圍環境之間為自然對流換熱，得到空氣溫度隨時間變化的曲線如圖2所示。在電路板上八個直徑均為4 mm的通孔內側面添加固定約束，來模擬電路板通過螺栓夾裝在盒體內的工作狀態。

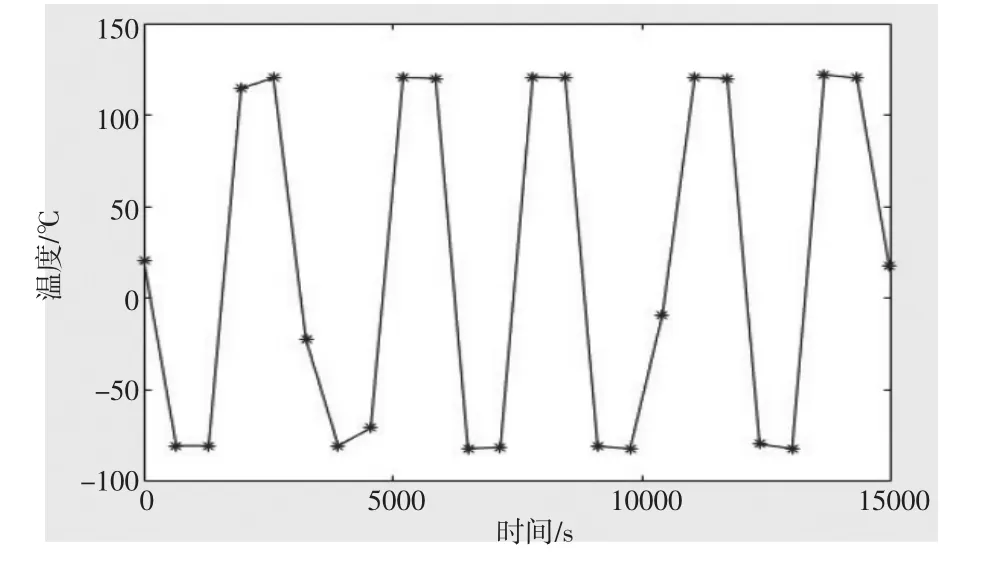
圖2 溫度載荷隨時間變化的曲線

圖3 為熱循環載荷作用下電路板在最后一個周期內不同時刻的溫度分布云圖。

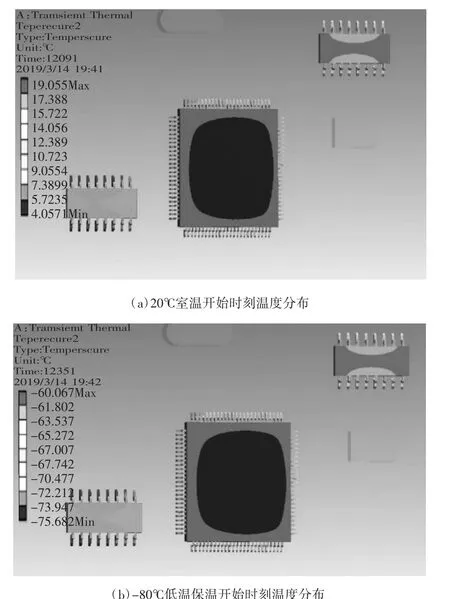
（續下圖）

（接上圖）

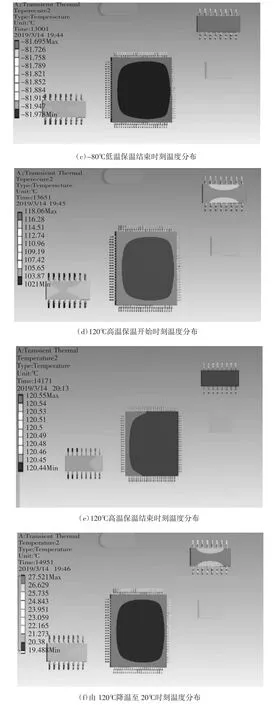
圖3 熱循環載荷作用下不同時刻的溫度分布云圖

當溫度載荷從120℃降低至20℃時（t=12 091 s），如圖 3（a）所示，電路板整場溫度差約為 15 ℃，且最高溫度位于小外形封裝焊料位置處；隨著環境溫度從 20 ℃下降至-80 ℃（t=12 351 s），如圖 3（b）所示，電路板各處溫度降低，但由于熱量傳輸的滯后性，在低溫保溫初始時刻電路板最低溫度僅到-75℃，且結構存在15.6℃的溫度差；當環境載荷在-80℃持續保溫650 s后，如圖3（c）所示，結構各處溫度逐步趨于穩定值，且電路板溫度差顯著減小至0.3℃，電路板與周圍環境溫度達到相對熱平衡狀態。從t=13 001 s時刻開始，環境溫度從-80℃逐漸上升至120℃（t=13 654 s），電路板上各器件溫度隨之提高，如圖3（d）所示，其中四方扁平封裝芯片表面溫度最高，達到了118℃，而小外形封裝焊腳溫度最低。這種溫度分布趨勢主要是因為芯片的導熱系數高于焊料，導致其熱阻相對較小，熱量更容易經其結構進行傳輸。隨著高溫保溫階段的開始，如圖3（e）所示，結構各處溫度上升至120℃，且至高溫保溫結束時刻（t=14 171 s）溫度場差異下降至0.1℃。

2.2 電路板應力應變響應特性

熱循環載荷作用下電路板最終時刻的總位移云圖如圖4（a）所示。由圖可知，電路板在八個通孔處的變形幾乎為0，這是由于電路板通過八個螺栓與外部盒體固定，在溫度載荷作用下幾乎不會產生變形位移。同時，可以發現在熱循環結束時刻總位移最大處位于右上方小外形封裝的上側焊點處，具體位置如圖 4（b）所示。

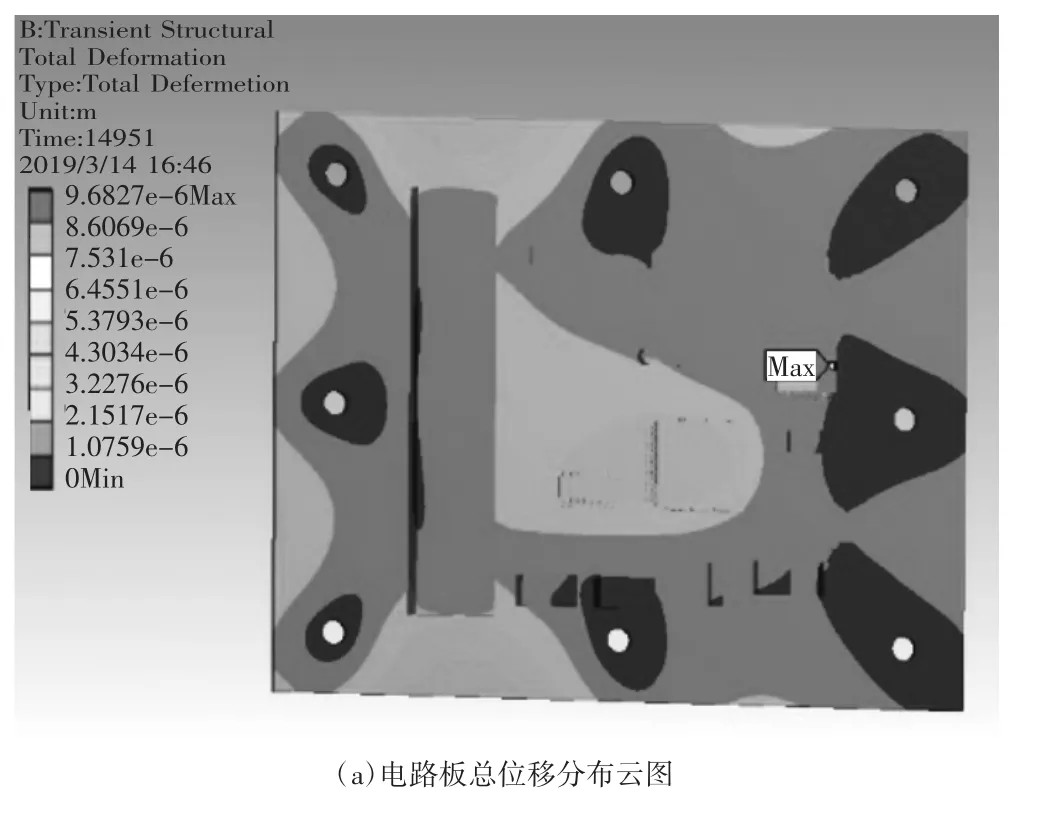
（續下圖）

（接上圖）

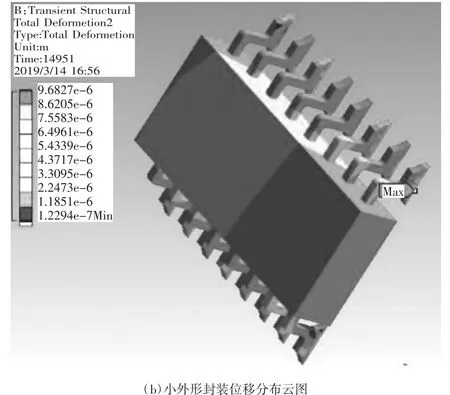
圖4 熱循環結束時刻位移分布云圖

如圖5所示為溫度與結構位移最大位置隨時間的變化曲線。由圖可知，當溫度發生變化，即不論是升溫還是降溫階段，由于環境載荷發生變化，電路板各處溫度出現差異，結構在約束作用下產生變形，且總變形量會隨載荷的變化近似線性增加。但當處于環境載荷進入保溫階段，即環境溫度不隨時間發生變化，電路板上各處溫度趨于穩定值，總變形量也維持相對穩定。同時，可以發現相較于低保溫階段，結構在高保溫階段的總位移更高。

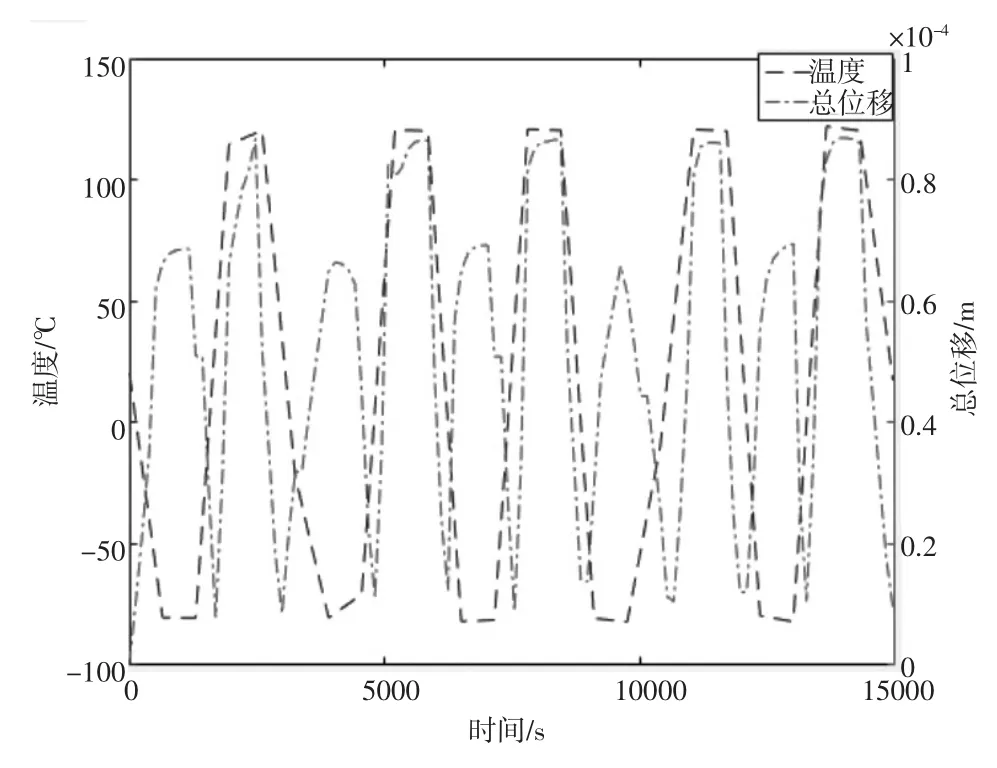
圖5 溫度與總位移隨時間的變化曲線

圖6 為電路板在循環結束后危險焊點的應力和應變云圖。由圖6（a）可知危險焊點的等效應力分布差異明顯，危險位置位于引腳與焊點交界處，最大值達到15.429 MPa；由圖6（b）可知危險焊點，應變最大值達到0.103 73，且同樣位于引腳與焊點交界處。

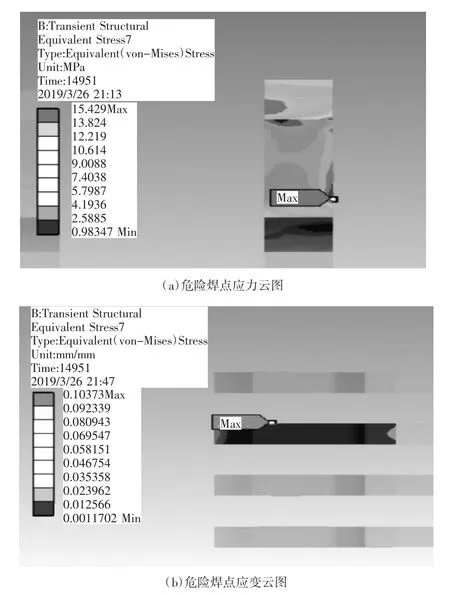
圖6 循環結束時刻危險焊點應力應變云圖

圖7 為溫度載荷與電路板等效應力最大位置隨時間的變化曲線。由圖可知，當環境溫度從20℃升高至120℃或降低至-80℃過程中，結構內產生溫度差異，且其隨著載荷變化而改變，且又由于各部分熱膨脹系數的不同，導致結構彎曲變形且各部分相互牽制，結構產生較大的應力，但當環境載荷進入保溫階段，即環境溫度不隨時間發生變化，電路板與環境載荷逐步達到熱穩定狀態，其上各處溫度趨于穩定值，等效應力也維持相對穩定。

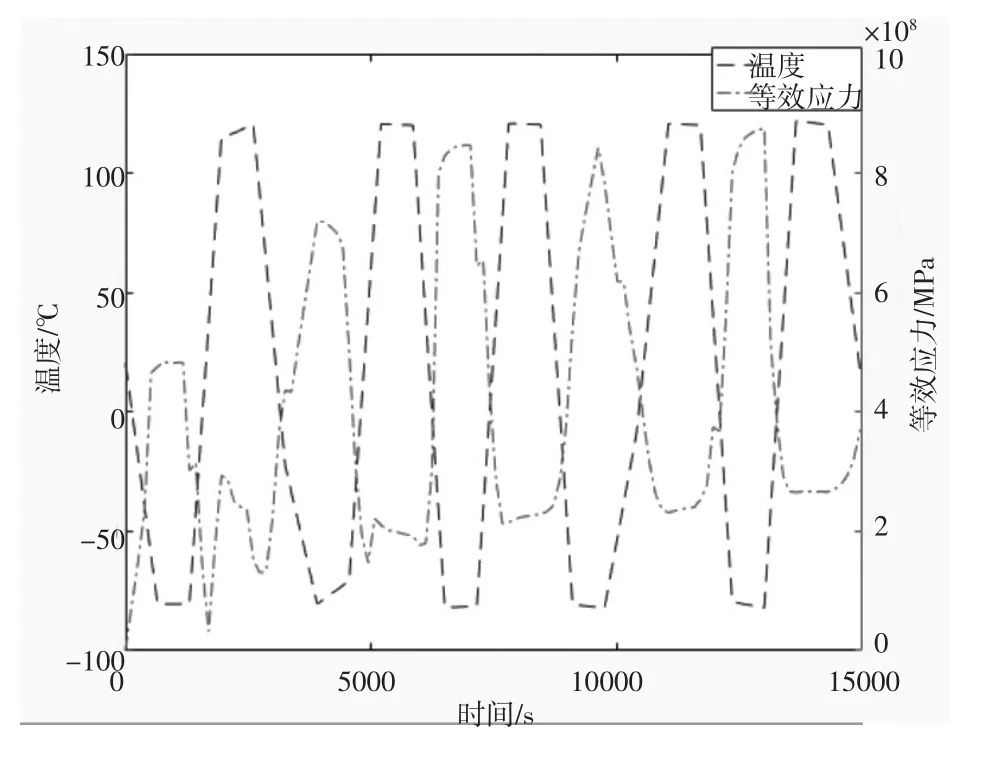
圖7 溫度和等效應力隨時間的變化曲線

3 結束語

本文建立了板級電路熱—結構耦合加載有限元模型，并利用模型分析了板級電路的溫度場分布及變形應力應變響應規律。由云圖可知，電路板整體結構從低保溫初始時刻、高保溫初始時刻開始，隨著保溫時間的持續，整體結構溫度差顯著下降，最終結構與環境溫度趨于平衡狀態。電路板溫度發生變化時，等效應力也隨之變化，并且等效應力和等效塑性應變危險位置均位于引腳與焊點交界處。