基于改進SVDD算法的升降機軸承故障檢測研究

劉俊辰，唐文秀，金劍橋，吳俊英

(東北林業大學 機電工程學院， 哈爾濱 150040)

升降機是工業及物流領域重要的機械設備，保證其安全可靠運行十分重要[1]。升降機軸承故障是其運行過程中的主要故障，然而升降機軸承運行過程中的故障數據只是很小一部分，正常數據占絕大部分，所以故障數據相當容易缺失，導致數據不均衡。能夠及時檢測出升降機軸承振動信號的負類樣本，就能及時維修或更換該部分的設備零件，防止由單個零部件的故障造成整個設備停止運作[2]。

目前升降機軸承故障檢測主要有基于傳統的計算機統計學習方法的故障檢測方法和基于支持向量機(support vector machine，SVM)的故障檢測方法。計算機統計學習方法具有計算精度高的特點，因此一直是軸承故障的主流檢測方法，但是計算機統計學習方法不能很好地做到將大數據樣本進行小樣本數據分類，并且容易出現局部最優解問題，無法滿足精準檢測故障數據的要求[3]。SVM算法的出現很好地解決了這一問題。SVM算法最開始用于研究二分類問題，是一種以傳統學習理論和結構風險最小化的機器學習方法[4-5]。當SVM面對不均衡數據時，學習后的分類界面會向故障樣本類別偏移，導致SVM對故障樣本產生很大的泛化誤差。李勇發等[6]針對此問題提出一種不同于二分類法SVM的基于支持向量數據描述算法(support vector domain description,SVDD)的軸承故障檢測方法。這是一種單類分類方法，其目標與傳統回歸問題或分類問題相區別，是為了通過機器學習得到一類樣本數據的特征描述， SVDD將囊括整個樣本數據集的目標樣本并將其他不屬于該類的樣本拒絕在其創造的空間之外[7]。然而，單類分類器SVDD在機器學習的過程中，只考慮正類目標樣本，不考慮少數樣本信息對決策邊界的影響，使得優化后的決策界面靠近多數類樣本一側，導致算法的召回率性能不高。顯然，基于此描述方法對升降機軸承故障檢測不夠全面，精度不足。

為此，本文提出一種基于帶負類樣本的支持向量數據描述算法(support vector data description with negative example,SVDD-NE)。該算法考慮所有的訓練樣本集，兼顧不同少數類樣本組合的局部結構信息。本文采用SVDD算法和SVDD-NE算法對升降機軸承數據進行實驗，驗證了該算法在升降機軸承故障檢測中的有效性。

1 改進支持向量數據描述算法

1.1 支持數據向量描述算法(SVDD)

SVDD算法是經典的單分類算法，通過尋找包括所有正常樣本最小化超球體的方式確定最優分類界面[8-9]。該模型在訓練時不依賴其他類別的樣本，因此非常適用于處理不均衡數據集的分類問題，尤其是在缺少異常訓練樣本的情況下。其簡要數學模型如下：

(1)

約束條件為：

(〈xi-a,xi-a〉)≤R2?i=1,2,…,N

(2)

其中：R為超球體半徑；a為圓心；N代表所有同類訓練樣本的個數。求解包含所有訓練樣本xi的最小超球體。引入核函數后由拉格朗日最優化理論，可以得到上述問題的對偶問題：

(3)

約束條件為：

(4)

αi≥0,i=1,2,…,N

(5)

SVDD算法因只關注正常樣本信息而不需要異常樣本參與訓練學習，使得優化后的分類界面偏于正常樣本一側，從而導致算法分類性能不高[10]。

1.2 帶負類樣本的數據向量描述算法(SVDD-NE)

為解決SVDD算法存在的問題，提高升降機軸承故障檢測精度，本文提出一種改進的支持向量描述算法，即帶有負類樣本數據分析的支持向量數據描述方法(support vector domain description with negative examples，SVDD-NE)，該算法利用負類樣本信息調整分類邊界，通過對正類和負類樣本增加不同懲罰因子的方式使其向負類樣本方向偏移，進而提升算法的分類性能。建立數學模型目標函數如下：

(6)

約束條件：

(xl-a)T(xl-a)≤R2+ξl,ξl≥0,

?i=1,2,…,n

(7)

(xm-a)T(xm-a)>R2-ξm,ξm≥0,

?m=1,2,…,n

(8)

其中：R為超球體半徑；a為超球體的球心；C1C2用于控制正常和異常訓練訓練樣本損失函數的大小，即懲罰因子；ξ1,ξm是正類樣本和負類樣本的懲罰因子，用來平衡正類樣本和負類樣本之間的距離比例。

將約束條件代入目標函數，加入乘子αl≥0,αm≥0,λl≥0,λm≥0，得到拉格朗日函數：

(9)

對式(9)變量求偏導并令其為0，得約束條件為：

(10)

(11)

(12)

(13)

將以上約束代入原問題得到對偶函數，并使用核函數將樣本點映射到高維特征空間中：

(14)

求解以上凸二次規劃問題，得球心

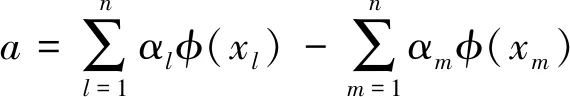
(15)

SVDD-NE算法由于使用了全部樣本數據，使得訓練精度提高，也使SVDD算法分類性能得到大幅度提高。

利用SVDD-NE算法對正、負兩類測試樣本數分別是100和10的數據進行分類試驗，其中參數C=10，高斯核函數的核半徑參數為σ=3，結果如圖1所示。可以看出，本文提出的SVDD-NE算法在處理不均衡數據線性可分問題時得到的分類界面趨于兩類中間。這是由于該算法中充分考慮了異常類樣本和正常類樣本，使得分類界面向著2類樣本集的中間靠攏，從而提高算法的泛化能力。

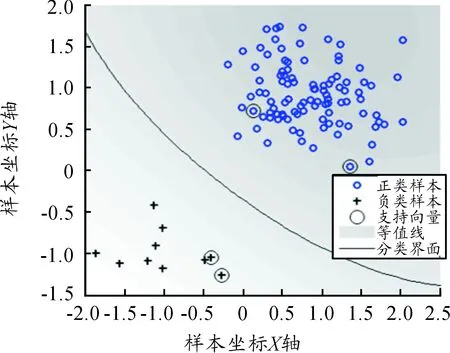
圖1 SVDD-NE算法分類結果示意圖

2 升降機軸承故障檢測仿真實驗

本文實驗使用升降機軸承數據來進行，實驗數據的收集采用加速度振動傳感器通過永磁體將傳感器牢固地吸附于升降機軸承對應側面的中間位置[11-12]。本文對收集的振動信號分別按時間序列間隔化分段處理，得到采樣點數為1 024、樣本點數各為1 000的4種類型的振動信號片段集合。圖2為正常樣本、內圈故障樣本、外圈故障樣本與滾動體故障樣本的時域信息與經FFT變換后的頻譜信息。

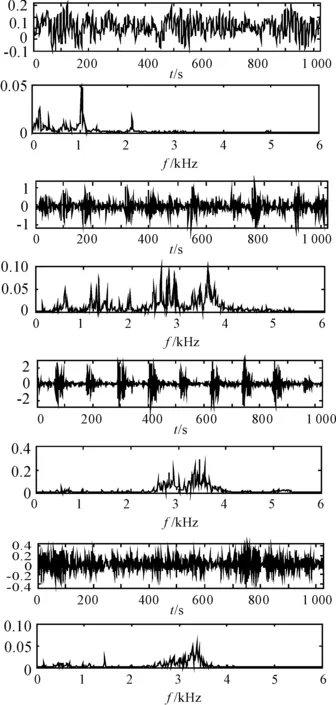
圖2 正常、內圈、外圈和滾動體故障樣本的時頻圖

從圖2可以看出，直接得到的振動信號時頻不能作為特征用作故障檢測[13]。因此，本文采用小波包分解的方法提取采集到振動信號的高維頻譜特征，并計算出每個小波包節點的熵(EWPN)與相對能量(REWPN)，且高維頻譜特征對不同類型間的故障樣本區分度不強，為了獲得4種不同振動信號區分度較強的低維特征集合，采用KECA方法對所得到的高維特征向量進行降維[14]。

2.1 升降機軸承故障檢測流程

針對不均衡數據下的升降機軸承故障檢測問題，本文提出一種基于SVDD-NE算法的軸承故障檢測模型。具體流程如下：

1) 對采集到的軸承振動信號分別按時間序列間隔化分段處理，得到采樣點數為1 024、訓練樣本個數為N的振動信號片段集合D∈R1 024×N。

2) 對D∈R1 024×N，利用小波包分解變換(wavelet packet decomposition，WPD)對每個訓練樣本分別進行時頻分解，其中,小波包函數采用DB2小波，分解為L層，分別得到2L小波包節點，得到訓練樣本振動信號的小波包節點系數集合C∈R(2L×WPNL)×N, WPNL=1 024/2L為每個小波包節點系數的個數。

3) 對C∈R(2L×WPNL)×N，分別求每個小波包節點的熵(entropy in a wavelet packet node，EWPN)和小波包節點的相對能量(relative energy in a wavelet packet node，REWPN)，得到訓練樣本振動信號的高維頻譜特征集合X∈R2L+1×N。X=[x1,x2,…,xN]為2L+1×N型矩陣，N是訓練樣本數，其中：

xi=[EWPN(i1),…,EWPN(i2L),REWPN(i1),…,

REWPN(i2L)]T,i=1.2,…,N

(16)

(17)

(18)

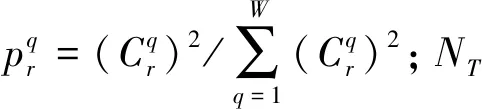
4) 對X=[x1,x2,…,xNr]進行核熵成分分析，通過將原始高維觀測空間投影至維數為d的低維特征空間以獲得低維特征XKECA∈Rd×N。

5) 對XKECA帶入 SVDD-NE檢測器進行訓練。

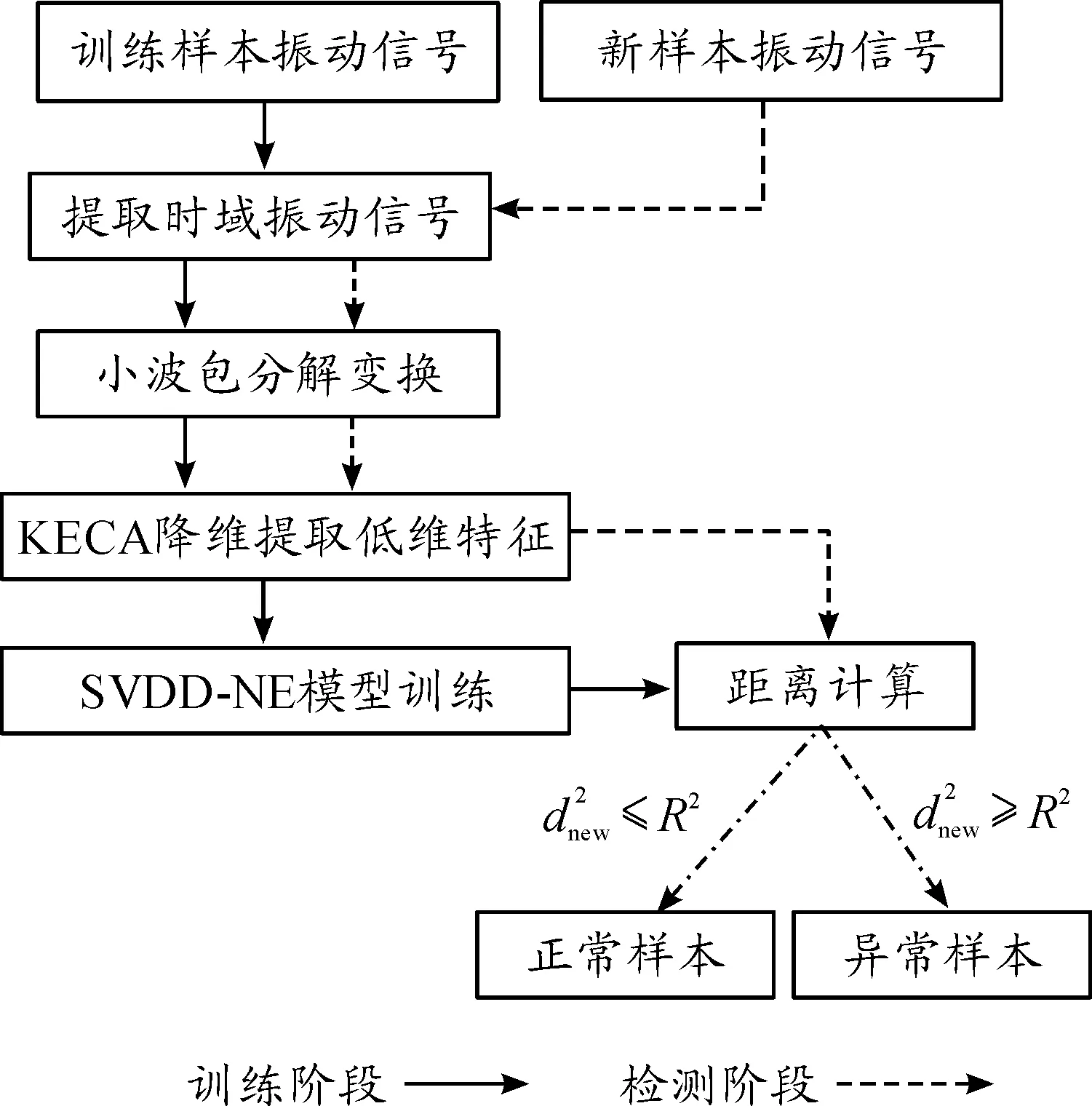
圖3 基于SVDD-NE的升降機軸承故障檢測流程

2.2 分類模型參數選取

對于不同的支持向量機分類方法，對應的最佳參數一般是不相同的，為了比較的客觀性，實驗中選取的均是各種方法對應的最佳參數。這個實驗中的核函數只選擇高斯核函數，并且各個超球面支持向量機用同一個核函數參數σ，但與超平面的核函數參數不同。為了能使SVDD-NE和SVDD達到各自的最優分類效果，先要進行模型參數的選取。在以下分類圖中“○”為正常數據(正類樣本值)，“+”為故障數據(負類樣本)。同時也要避免過擬合現象。

1)實驗1：SVDD-NE分類器的參數選取。首先對于高斯核參數σ的選取，先固定懲罰因子C1=10,C2=10，分類精度在圖4注釋標出。

從以上實驗分類圖直觀可知，當高斯核函數σ過小時，數據分類容易產生過擬合現象。當σ=4時，分類精度為0.91且分類球體體積最小，所以取σ=4為SVDD-NE的高斯核參數。接下來選取懲罰因子。

從圖5中可以看出，當σ=4,C1=10,C2=10時，構造的超球體描述覆蓋的體積最小，當懲罰因子增大時其體積也隨之增大。所以選取σ=4,C1=10,C2=10作為最佳參數，分類精度為0.91。

圖4 高斯核參數σ的選取對算法的分類性能影響

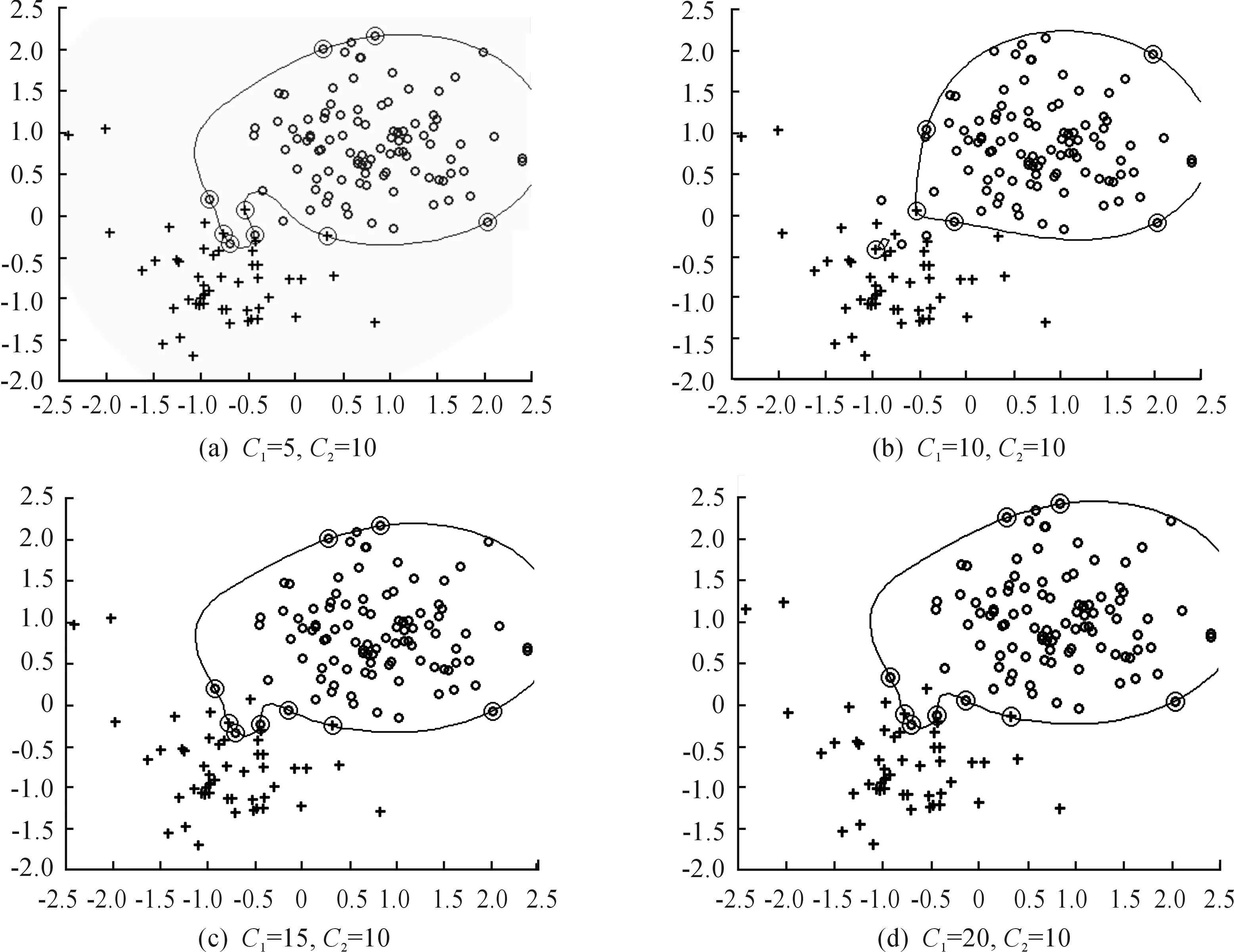
圖5 懲罰因子選取對算法性能的影響

2) 實驗2：SVDD的參數選取。對于高斯核函數σ的選取，采用上述相同實驗方法對SVDD分類模型的參數進行選擇，結果表明：當σ=1，分類精度precision=0.85，且超球體包裹體積最小，為SVDD的最佳參數。

2.3 升降機軸承故障檢測仿真實驗

為了驗證SVDD-NE算法與SVDD算法在升降機軸承故障檢測中的性能，實驗中將將2種算法檢測結果進行比較，選擇故障實驗模型為上述訓練出來的SVDD-NE和SVDD分類模型來進行升降機軸承故障值檢測。對收集到的數據進行歸一化處理，抽取70%的數據作為訓練數據。選取軸承正常數據(正類樣本)100組，故障數據(負類樣本)各50組，其中每個樣本都是經KECA降維后提取的低維特征。

實驗參數為：本文算法的高斯核函數參數σ=4，懲罰因子C1=20,C2=10；SVDD算法高斯核函數參數σ=1。

本次實驗采用十折交叉驗證法來進行多次實驗降低誤差。用SVDD分類器和SVDD-NE分類器對選定好的故障數據進行分類，用分類準確率來衡量分類性能。所有實驗均在i5CPU，1.8 GHz，內存4 G的計算機上進行，利用Matlab2010b軟件。

從圖6～8中不難發現，SVDD算法因只關注升降機軸承正常樣本信息而不需要異常樣本參與訓練學習，使得優化后的分類界面偏于正常樣本一側，從而導致算法分類性能并不高,造成對升降機各種軸承故障數據的檢測準確率較低[15]。

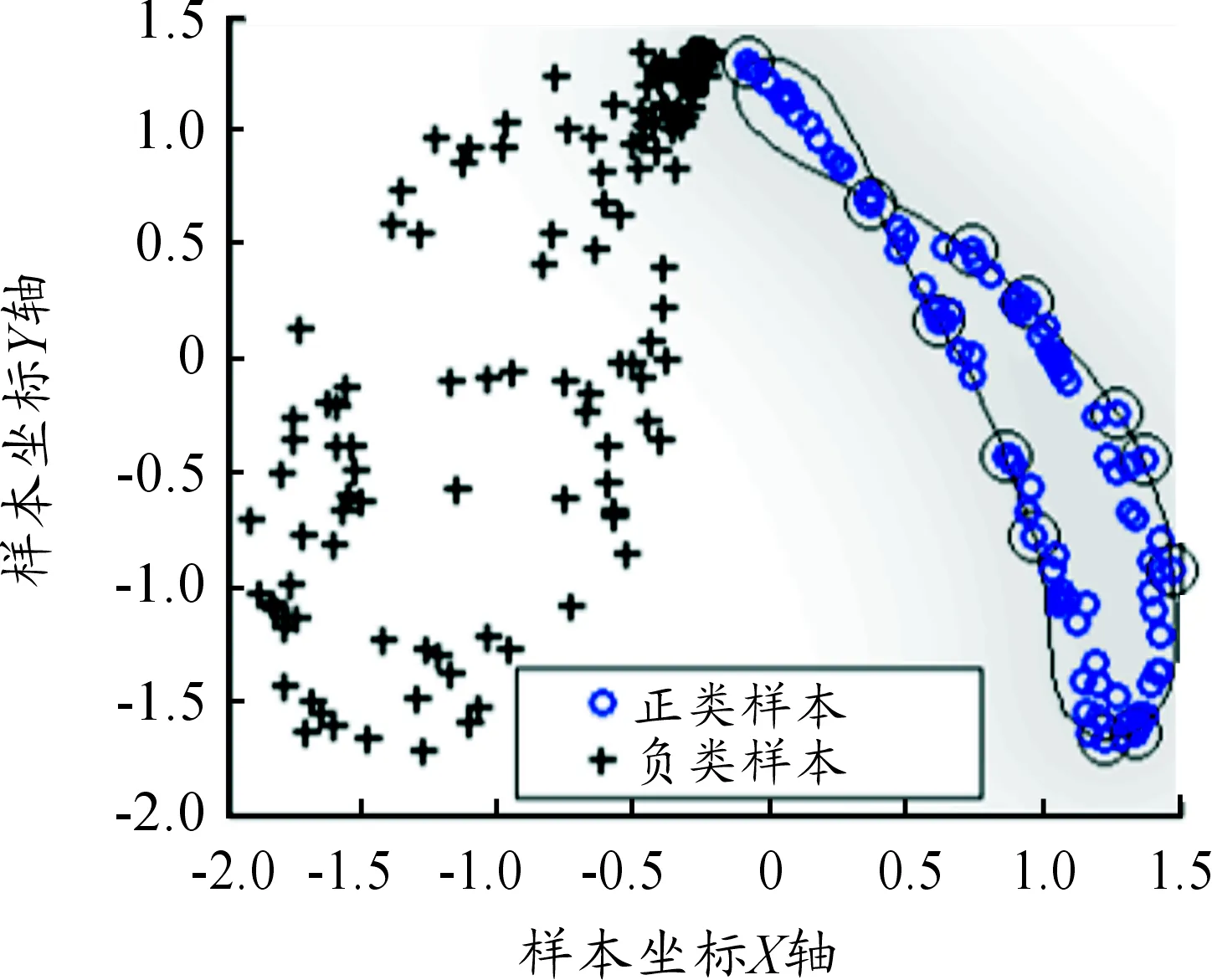
圖6 正常和內圈故障樣本經SVDD分類圖

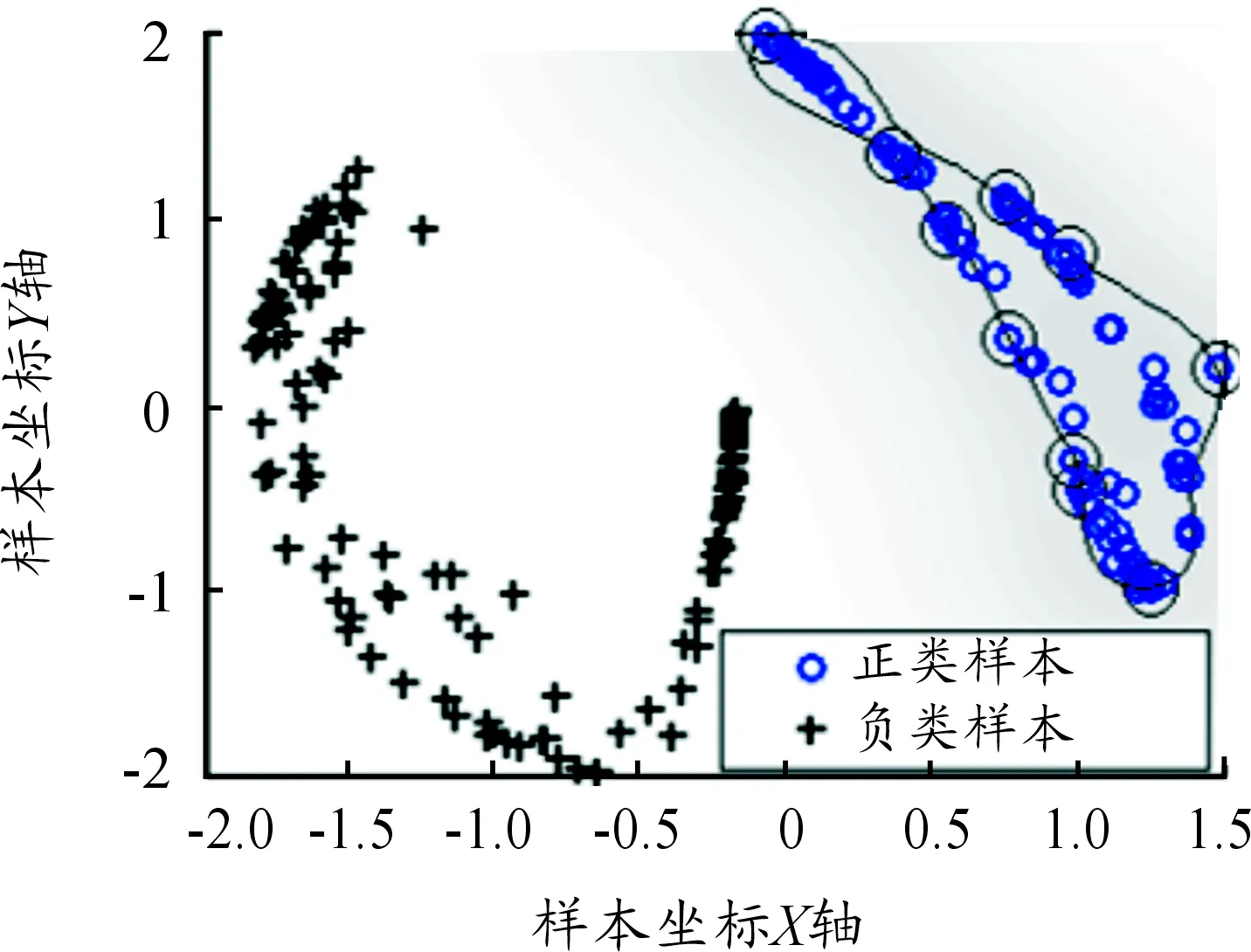
圖7 正常和外圈故障樣本經SVDD分類圖

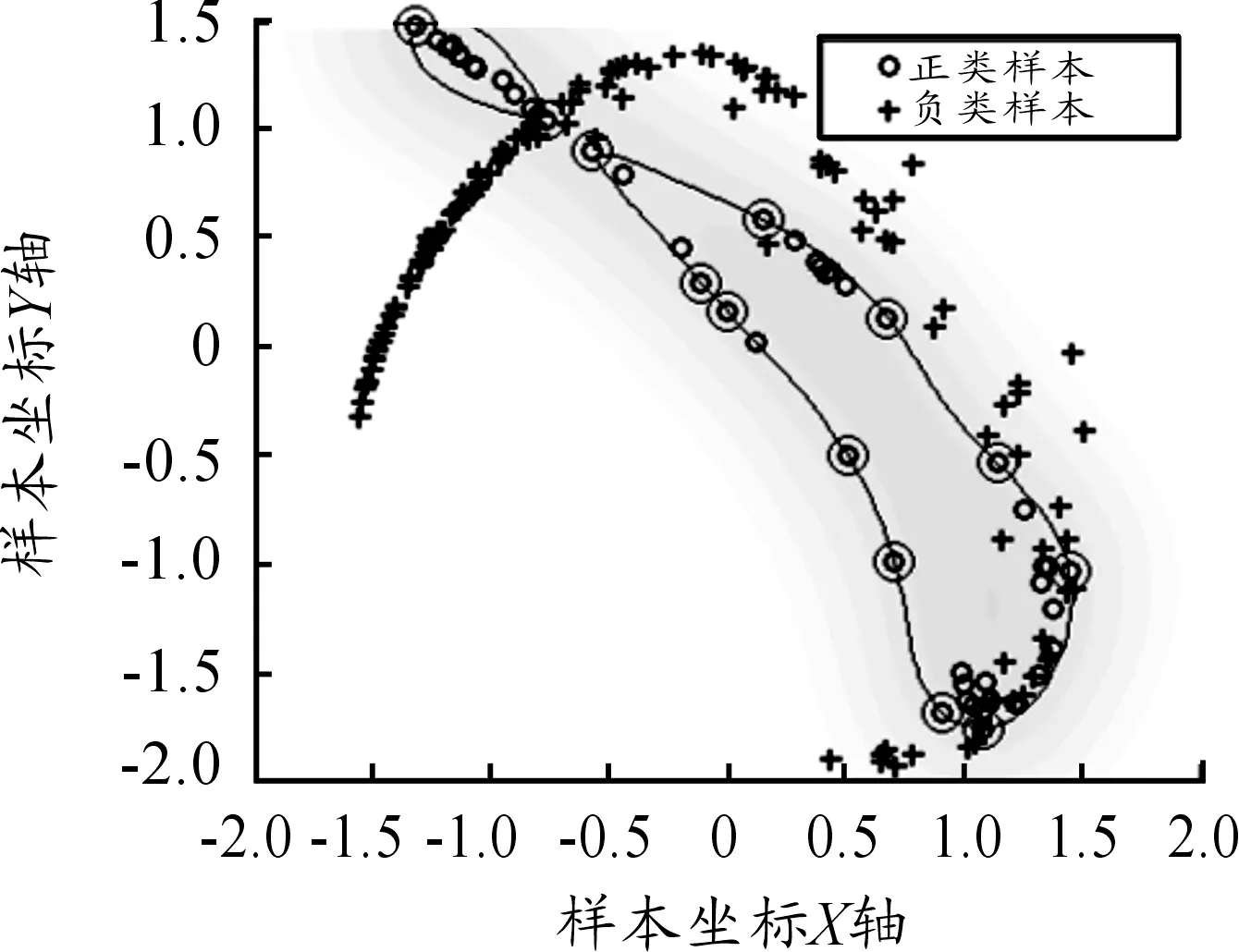
圖8 正常和滾動體故障樣本經SVDD分類結果圖

圖9 正常和內圈故障樣本經SVDD-NE分類結果圖

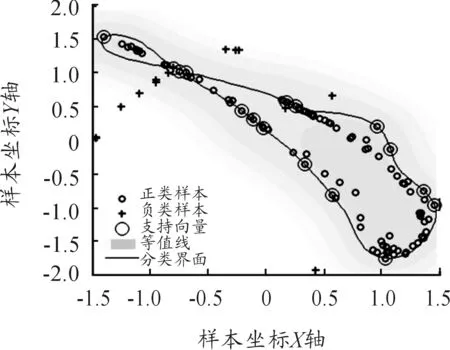
圖11 正常和滾動體故障樣本經SVDD-NE分類結果圖

通過對比可以看出：本文提出的SVDD-NE算法在處理升降機軸承不同種故障不均衡數據問題時得到的分類界面趨于兩類中間。這是由于該算法中充分考慮了異常類樣本和正常類樣本，使得分類界面向著兩類樣本集的中間靠攏，從而提高了算法的泛化能力。因此，本文提出的基于SVDD-NE算法的軸承故障檢測方法在針對升降機各種故障不均衡數據方面具有更好的性能。

實驗對升降機軸承振動故障數據的分類準確率結果如表1所示。通過結果可得：SVDD-NE的平均分類精度為0.92，SVDD的平均分類精度為0.88。

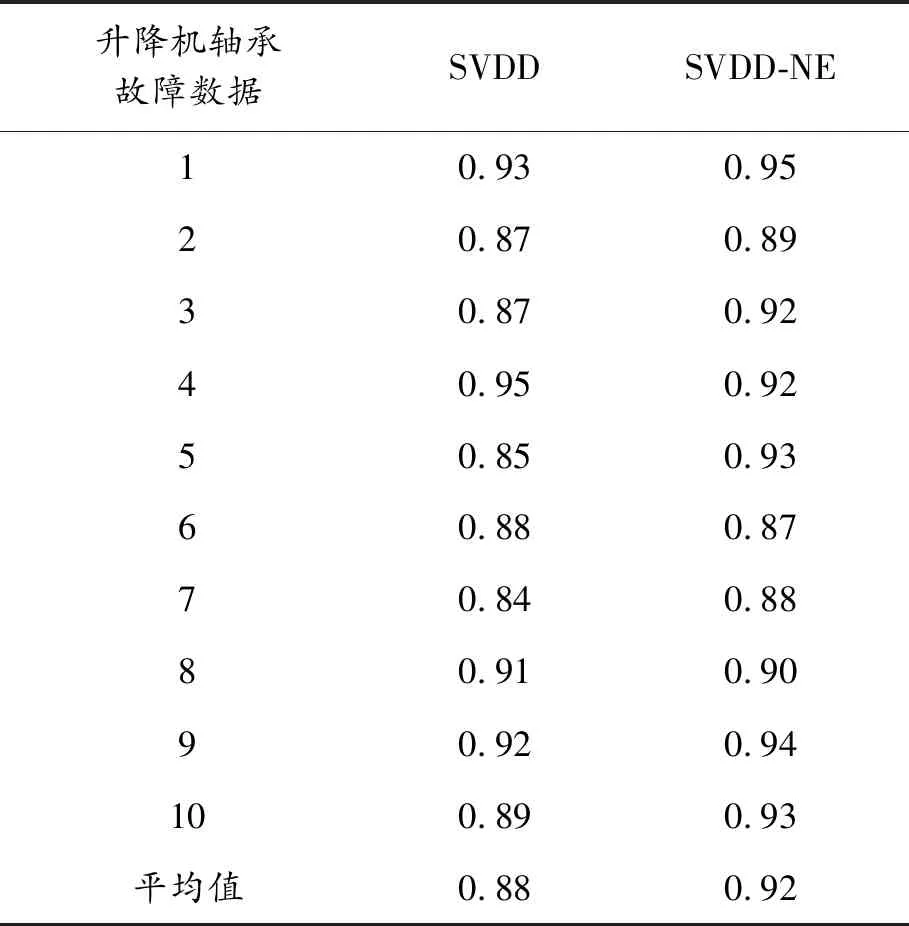
表1 升降機軸承故障數據分類準確率

從表1可以看出，本文提出的基于SVDD-NE算法的軸承故障檢測模型在解決升降機不均衡數據情況下的故障檢測問題時較SVDD算法的檢測性能有顯著提高，同時也進一步驗證本文提出的SVDD-NE算法比傳統SVDD算法在解決升降機軸承各種故障不均衡數據分類問題上具有明顯優勢。

3 結論

1) 針對升降機軸承故障檢測，相比傳統SVDD算法，本文所提出的基于SVDD-NE算法，在檢測精度上有較大提高，針對升降機軸承不同種故障都具有很好的檢測性能，能很好地運用于升降機軸承異常值檢測實際中。

2) 實驗結果表明，在數據不均衡情況下，加入負類樣本值作為SVDD的學習對象，其分類精度明顯改善。由此可知，SVDD-NE算法相較于SVDD算法，其分類性能顯著提高。