復雜動力學網絡系統在隨機采樣控制下的一致性分析

葉志勇,匡 艷,張 華,2,王澤權,林聰偉

(1.重慶理工大學 a.理學院; b.機械工程學院, 重慶 400054; 2.銅仁學院 大數據學院， 貴州 銅仁 554300)

在過去幾十年中，復雜動力網絡在生物神經網絡、互聯網、智能電網和人類社會網絡等領域得到了廣泛的應用[1-9]，引起越來越多的研究者關注。到目前為止，許多研究者已經提出了各種控制方案來處理復雜動力網絡的問題，如反饋控制[1]、自適應控制[2]、魯棒控制[3]和脈沖控制[4]。

對復雜動力網絡系統的采樣控制主要從固定拓撲、切換拓撲；有向圖、無向圖；有時滯、無時滯等方面進行研究。文獻 [5]討論了Kuramoto-Sivashinsky 方程的分布式采樣控制，對n個傳感器在空間上提供時間采樣，并在采樣空間間隔上對狀態的分布進行測量。文獻[6]考慮了脈沖輸入時滯，對非線性復雜動力系統的指數同步問題進行了探討。當隨機抽樣是一個伯努利分布時，考慮兩個不同的采樣周期，若發生概率為已知常數，則文獻[7]將原始隨機采樣的馬爾可夫跳躍系統轉化為連續性馬爾可夫跳躍時滯系統，從而研究輸入飽和隨機抽樣馬爾可夫跳躍系統的控制問題。文獻[8]討論了二階多智能體系統在通訊網絡拓撲固定的情形下，對于不同的動力學行為給出更準確的代數判據。

對于復雜動力網絡的穩定性而言，其中一致性問題是最重要的行為之一。復雜網絡系統的一致性研究目前有很多研究成果[9-11]。文獻[9]分別得到了在固定的拓撲結構下的一致性和在切換拓撲結構下利用多項式的Hurwitz穩定性，得到了帶有采樣信息的一致性。對于一般線性動力學，文獻[10]討論了帶有時變采樣間隔的多智能體系統的采樣數據一致性問題。為了滿足1階多智能體系統漸近平均一致性的充要條件，文獻[11]采用時滯分解技術，在離散時間下得到了一致性協議，從而實現了系統的一致性。

本文將研究復雜動力學網絡系統在隨機采樣控制下的一致性問題。首先，建立復雜動力學網絡系統。其次，引入控制器，通過分布式可控輸入得到誤差系統。再次，選取合適的李雅普諾夫函數，利用輸入狀態穩定理論得到系統穩定的充分條件及采樣周期。

1 問題描述

1.1 預備知識

定義1[12]若非奇異實矩陣H的所有非對角線元素小于0，主對角線元素大于0，且H的特征值具有正實部，則非奇異實矩陣H是M矩陣。

引理1[13]對于適當維數的矩陣A、B、C和D，下面的性質成立：

① (μA)?B=A?(μB)，μ是常數；

② (A?B)(C?D)=(AC)?(BD)；

③ (A?B)T=AT?BT；

④ (A+B)?C=A?C+B?C。

引理2[13]假設X∈RN×N是一個M矩陣，則存在正向量η=(η1,η2,…,ηN)T∈RN，使得XTη=1N且ΩX+XTΩ>0，其中Ω=diag{η1,η2,…,ηN}。

引理3[14]設V:[0,+∞)×Rn→R是連續可微函數滿足下面的不等式：

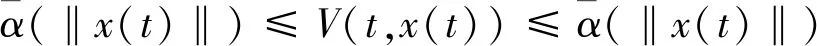
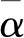
串聯式系統是狀態輸入穩定的一個重要推廣，如下：

(1)

(2)

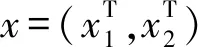
引理4[14]當x1是輸入時，若動力學系統(2)在x1下為狀態輸入穩定，且原系統(1)是全局一致漸進穩定的，則串聯式系統(1)和(2)是一致漸進穩定的。

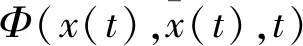
(3)

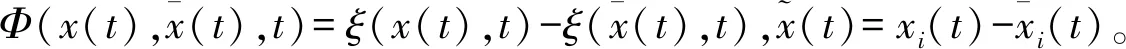
1.2 模型描述

本文考慮如下的復雜動力學網絡系統模型:

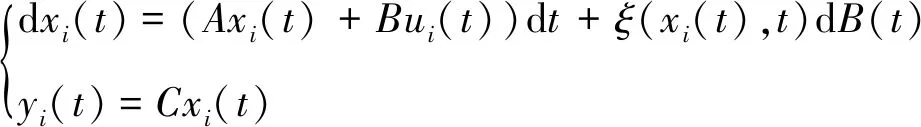
(4)

在實踐和工程應用中，信息的狀態不是一直都可以進行訪問的，從而導致了在設計控制輸入時需要利用輸出可測的yi(t)。假設輸出yi(t)在連續時間下的采樣時刻tk是可測的,且控制輸入在零階保持器方案下生成。因此，在節點i的分布式可觀測的響應狀態方程描述如下：

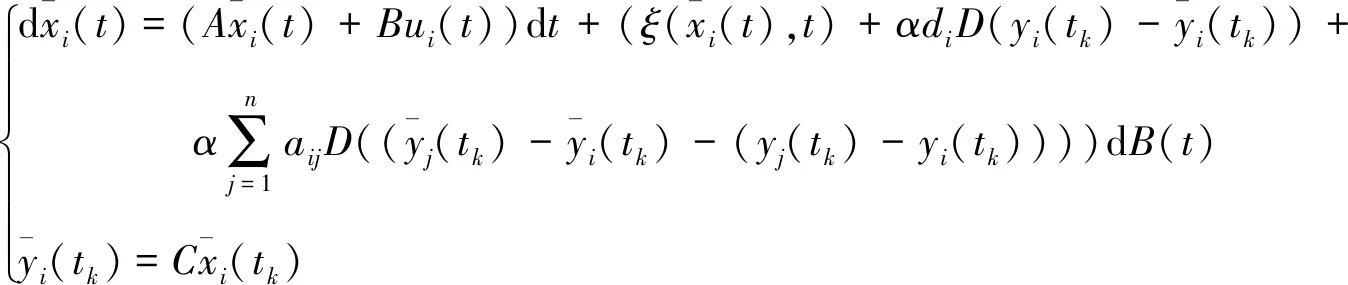
(5)

其中分布式可控的輸入響應設計為

(6)

這里，di={0,1}，di=1時，當且僅當第i個節點在采樣時刻tk是確定的輸出誤差估計。

注1本文將采樣信息時刻作為信息連接節點，即隨機擾動中含有采樣時刻[9-11]，隨機項中不含采樣信息，因此本文更符合現實。

為了后面方便計算，采用以下的記法：

di=1時，方程簡寫為：

(7)

di=0時，方程簡寫為：

(8)

2 主要結果

以下將對系統(7)和(8)進行一致性分析，其詳細的過程和結果由定理1給出。

定理1在假設1下，若反饋增益矩陣D、F是正定的，滿足下面的線性矩陣不等式：

(9)

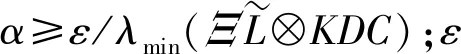
(10)

以及采樣周期滿足

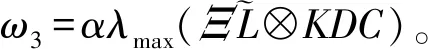
情況1在系統(7)下進行考慮。

證明首先，建立如下的Lyapunov函數：

(11)

其中K是正定矩陣。

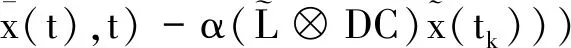
(12)

由于(Ξ?K)是正定的，則在式(12)中得：

(13)

根據系統(7)可得：

(14)

在式(14)中，第1部分得：

(15)

在式(14)中，第2部分得：

(16)

在式(14)中，第3部分得：

(17)

將式(13)～(17)代入式(12)得：

(18)

利用下面的不等式成立：

則，

(19)

這里

V1(t)=maxV(t)，t∈(tk,tk+1)

可知：

(20)

根據式(20)可知，需滿足下面的不等式：

因此，根據不等式(9)(10)和引理3可以得到LV<0。

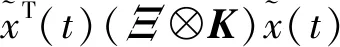
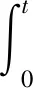
(21)

E(V(x,t))≤e-δ1tE(V(x0,0))

情況2在系統(8)下進行考慮。

證明首先，建立如下的Lyapunov函數：

(22)

其中K1是正定矩陣。

(23)

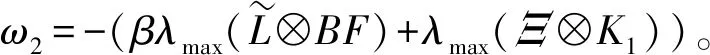
(24)

根據式(24)可知，需滿足下面的不等式：

-(λmin(Λ)-ω2)>ω2w1T

因此，根據不等式(9)(10)和引理3可以得到LV<0。

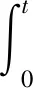
(25)

E(V(x,t))≤e-δ2tE(V(x0,0))

注2文獻[6]和[10]中的采樣信息是利用ISS穩定，僅檢查了V(x,t)的導數，在文獻[13]中增加了控制輸入，未考慮采樣的隨機性。本文考慮了采樣的隨機性，且將采樣的信息作為連接信息傳輸的節點和輸入控制，更具有現實意義。

3 數值模擬

為了驗證結論的有效性，對于復雜動力學網絡系統，在拓撲結構G下，通過用以下Chua’s電路描述動力學系統的每個節點：

(26)

現在將Chua’s電路方程改寫為下面的形式：

dxi(t)=Axi(t)dt+Ψ(xi(t))dB(t)

(27)

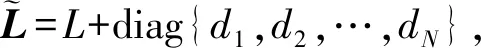
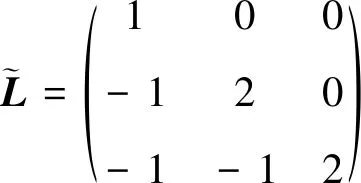
選擇參數β=0.846 7,α=56.449 7，通過利用LMI計算可得反饋矩陣F和觀測矩陣D

位置狀態的時間響應一致性軌跡在圖1和圖2中給出，則系統(7)和(8)實現一致性，因此理論的有效性就得以證明。

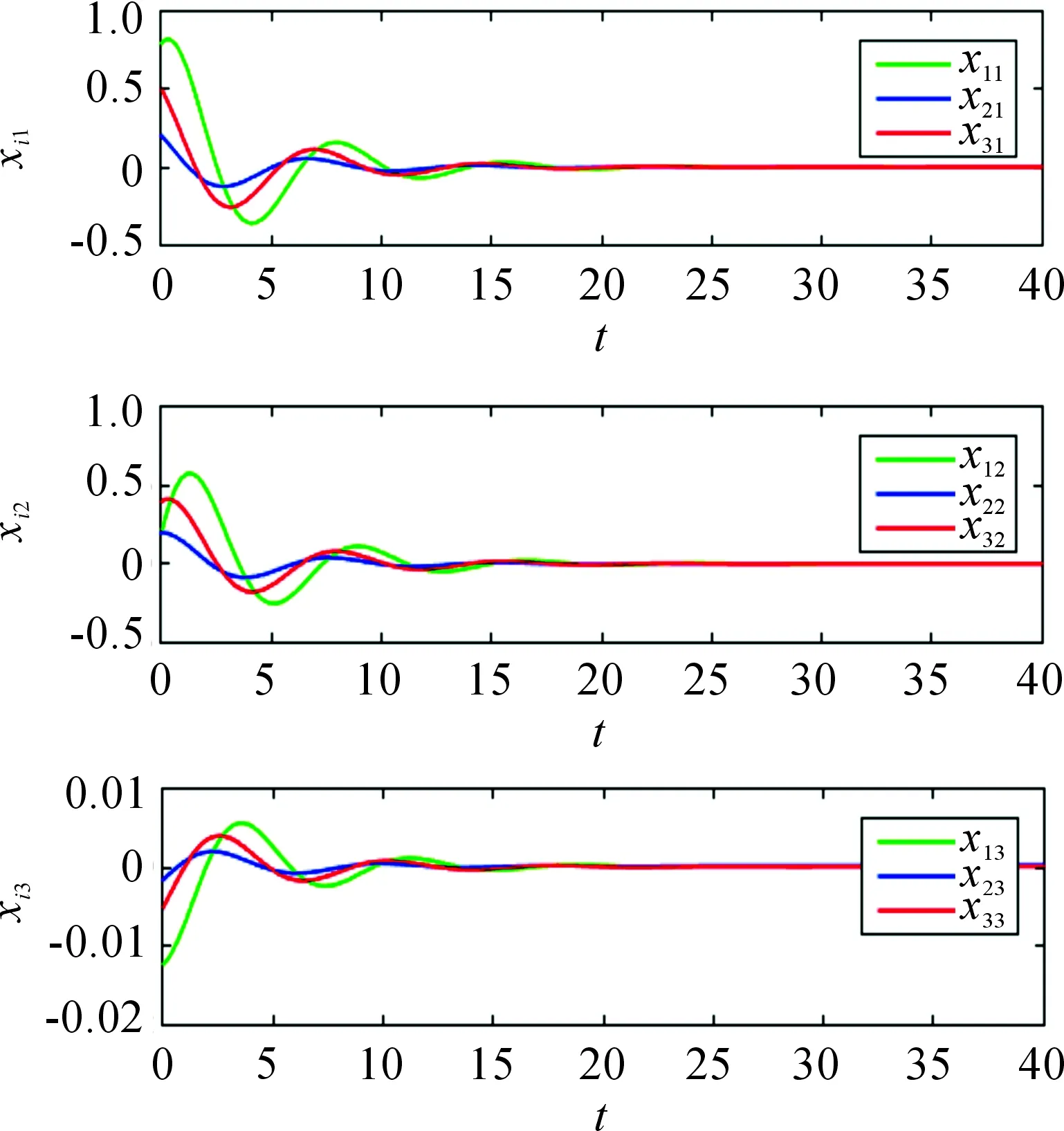
圖1 系統(5)的位置軌跡

4 結束語

本文研究了在無向拓撲結構中復雜動力學網絡系統在隨機采樣控制下實現一致性的問題。首先，建立不穩定的動力學系統，設計控制輸入，得到誤差方程。其次，利用Lyapunov函數和狀態輸入穩定理論得到系統穩定的充分條件，并說明Laplacian矩陣在分析系統穩定性問題中的重要性。再次，當系統滿足定理條件時，能夠達到一致性，并通過控制輸入參數和采樣周期使系統實現狀態輸入穩定。最后，通過數值仿真說明了定理的有效性。