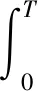有記憶項的弱退化波方程的精確零能控性

劉瑞娟

(山西大學 數學科學學院， 太原 030006)

本文研究有記憶項的弱退化波方程的精確零能控性:

(1)

退化偏微分方程具有可變耗散系數算子，使得方程在空間區域上是不一致的，而且退化可以發生在邊界的一部分，也可以發生在空間區域的子流形上，這使得研究這一類偏微分方程的精確能控性問題比較困難。 為了克服這一難點， 近年來研究退化偏微分方程的能控性問題，常用的方法有乘子法、矩方法、Carleman 估計等。

退化拋物型方程的控制問題在近10年來得到了廣泛的關注，已經有很多研究結果[1-6],但目前為止對退化波方程的研究比較少。文獻[7]利用HUM(hilbert unique method) 推導出退化波方程utt-(a(x)ux)x=0的狄利克雷邊界精確能控性，其中波的傳播速度a(x)稱為耗散系數。對于更一般的情形，即a(x)=xα， 文獻[8]通過對相應橢圓算子的譜來處理相關矩問題，推導出其對偶系統的能觀測性不等式，證明了退化波方程utt+(xαux)x=0在退化點x=0處的狄利克雷邊界精確能控性結果。 然而，在物理意義下，退化波在端點x=0處的傳播速度為0，若控制作用在該點上,那么它對整個波幾乎沒有影響。 但是當作用在非退化邊界時,對整個波的影響是持續的。 基于此，文獻[9]利用文獻[7-8]的方法證明了控制作用在非退化邊界時的精確能控性問題。

對于有記憶的非退化波方程， 文獻[11-12]得到了一些精確能控性的結果，而對于有記憶項的退化方程研究很少。文獻[10]利用矩方法研究了有記憶項的弱退化拋物方程的近似零能控。 為了研究有記憶的耗散項對弱退化波方程零能控的影響，本文利用文獻[11-12]的方法處理記憶項，進而得到有記憶項的弱退化波方程的精確零能控性。

1 預備知識

對任意的α∈[0,1)，定義空間

(2)

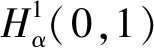
由Hardy-Poincaé不等式[6]

可得：

(3)

其中常數Cα>0。

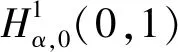
(4)

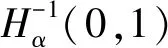
首先，給出精確零能控的定義。

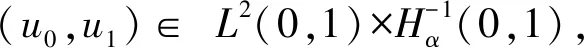
下面給出本文的主要結果：

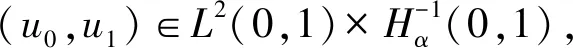
2 解的適定性

由文獻[13]的方法給出系統(1)弱解的定義。

定義2若對任意的f∈L1(0,T;L2(0,1))且滿足

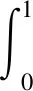
則稱函數

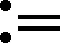
是系統(1)的弱解， 其中y滿足如下方程：

(5)

按文獻[7]的性質4.2的證明,可得系統(5)有如下性質：

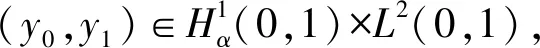
且滿足

C‖f‖L1(0,T;L2(0,1))

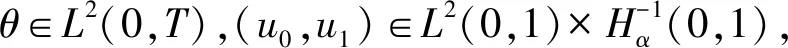
(6)

證明設f∈L1(0,T;L2(0,1)),則由性質1可得

C‖f‖L1(0,T;L2(0,1))

(7)

結合跡定理，可得

(8)

方程(1)兩邊同乘y，在Q上積分，可得

在空間L1(0,T;L2(0,1))上定義算子

(9)

由H?lder不等式以及式(7)(8)，可得

‖θ‖L2(0,T))‖f‖L1(0,T;L2(0,1))

因此,L是空間L1(0,T;L2(0,1))上的有界算子,即存在u∈H滿足式(9)，則式(6)成立,證明完畢。

3 能觀測性不等式

首先，考慮系統(1)的對偶系統：

(10)

為了計算方便，設φ(x,t)=ψ(x,T-t)，則

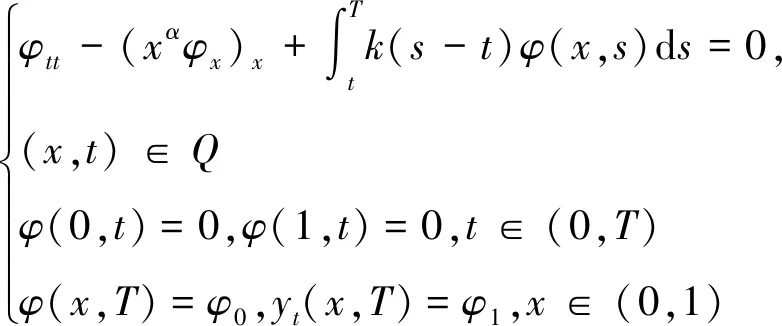
(11)

設

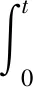
be-a(t-s)(a,b>0)

則ηt(t)=bφ(t)-aη(t),故系統(11)可寫為：

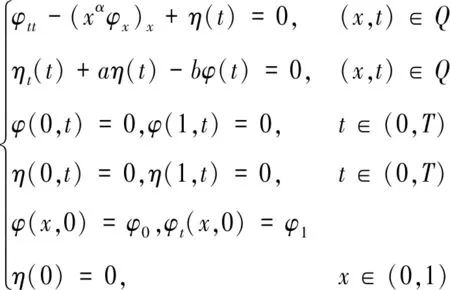
(12)

定義系統(12)的能量如下：

(13)

由η(0)=0可知:

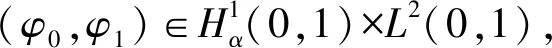
exp(-δt)E(0)≤E(t)≤exp(δt)E(0)

(14)

證明因為

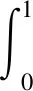
由(3)和Young不等式，可得

(15)

(16)

則

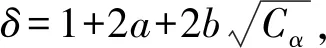
-δE(t)≤E′(t)≤δE(t)

(17)

從0到t積分式(17)，可得式(14)成立，證明完畢。

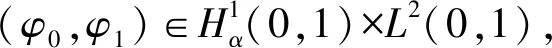
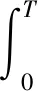
(18)

證明由式(12)兩邊同乘xφx，在Q上積分，可得

(19)

利用Young不等式有

(20)

其中常數ε,Cε>0。結合引理1估計等式(19)，可得式(14)成立,證明完畢。

注記1事實上，式(18)表明φx(1,·)∈L2(0,T)。

下面證明系統(12)的能觀測性不等式。

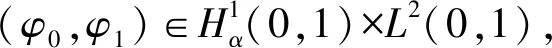
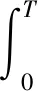
(21)

證明由式(15)兩邊同乘η，在Q上積分，可得

(22)

將式(19)和(22)相加，有

(23)

結合式(13)(23)可寫為

(24)

由式(15)(20)以及引理1可得

取足夠小的a、b、ε，使得

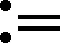
則

(25)

其中0<γ<(2-μ)(1-exp(-δT))/δ。

將不等式(14)的左邊在(0,T)上積分，可得

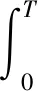
(26)

由式(25)和(26)有

((2-μ)(1-exp(-δT))/δ-γ)E(0)≤

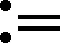
4 精確零能控性

下面證明系統(1)是精確零能控的。

定理1的證明

考慮如下系統：

(27)

式(27)乘以φ，在Q上積分， 其中φ滿足系統(11),可得

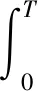
(28)

因此，可以選擇θ(t)=φx(1,t)。

定義映射

即Λ(φ0,φ1)=(u1,-u0),則式(28)可以寫為