新鮮產品跨季銷售中的動態庫存管理策略研究
龔媛媛,肖勇波
(清華大學經濟管理學院,北京 100084)
1 引言
現實生活中有很多新鮮產品(如蘋果、梨等),它們的采摘集中在較短的時間內,但是需求跨越多個季節。得益于經濟發展和人民生活水平的提高,反季市場的消費規模和市場潛力不斷增大,越來越多的新鮮產品分銷商采取跨季銷售的模式。2016年,我國第一大水果(蘋果)的貯藏量占到了總產量的37.7%,而山東煙臺、陜西延安和甘肅平涼等優生區采后的貯藏量更是超過了50%[1]。
相對于一般耐用品而言,新鮮產品在存儲和運輸過程中難免會發生變質,這給相關企業的經營管理帶來了更大的挑戰。為了減少新鮮產品在跨季銷售中變質帶來的損失,分銷商往往采用先進的冷藏保鮮技術(如氣調庫)和冷鏈物流體系。以贛南臍橙為例,過去從秋季采摘到銷售完畢,最長只有兩個月時間;但儲存在氣調庫中,銷售期可延長至6個月以上。但即便采用了氣調庫等保鮮努力,新鮮產品的質量(如外觀、質地、口感等)隨著時間的推移也會逐漸下降。常被消費者詬病的“黑心梨”就是在儲藏期間出現產品生理病害而導致的。質量的不確定性進一步加大了需求的不確定性,從而加劇了供需匹配的風險。在跨季銷售過程中庫存無法補給、產品質量又不斷下降的現實下,如何有效管理庫存是新鮮產品分銷商面臨的一個重大難題。他需要在當前確定的但可能較低的收益與未來不確定的但可能較高的收益之間進行權衡,動態決策采摘季節的初始庫存量以及每一銷售周期的庫存配給量,從而優化利潤。
易變質產品庫存管理一直是管理科學與工程領域學者和業界關心的熱點話題。初期的文獻大多聚焦于變質引起的數量損耗;對質量變質的關注始于Fujiwara和Perera[2],后續學者們結合不同的應用情景,通過將質量的瞬時變化率假設為服從某個特定分布[3]、直接給出質量變化的具體函數[4]以及將其假設為隨時間遞減的一般函數形式[5],對新鮮產品受質量變化影響的庫存管理問題展開了深入探討。例如但斌等[6]針對消費者在不同時刻購買新鮮產品的效用變化受新鮮度和價格影響的情形,建立EOQ模型并求解了不同保鮮條件下的最優訂貨決策;馮穎等[7]針對由供應商主導的物流服務水平影響產品新鮮度進而對市場需求產生影響的情形,建立三級供應鏈競合博弈模型,求解了供應商的最優定價、TPL服務商的最優服務水平以及零售商的最優采購量決策。
研究新鮮產品跨季銷售問題的文獻偏少,較有代表性的是吳國正[8],但與該文側重于研究旺季、淡季的價格變化對庫存配置的影響不同,本文關注的是產品變質因素的影響;此外,我們將淡季的銷售模型擴展到了多個周期的情形,并且利用動態庫存配給的思想加以求解。在已有的庫存配給文獻中,大多數學者假設系統可以多次補貨,對訂貨/產量決策和庫存配給決策同時進行優化(可參見張揚等[9]的綜述)。新鮮產品跨季銷售問題則不然,由于產銷發生了時間上的分離,分銷商無法在采摘期后再次補貨,需要決策的是比較特殊的“一次采購+多次配給”的聯合優化問題。該問題也可以看作是考慮需求配給的報童問題,代表性文獻包括Sen和Zhang[10]以及汪小京等[11]。類似于肖勇波和龔媛媛[12]針對分銷商采購一批新鮮產品后依次運輸至多個市場銷售的研究,我們同樣構建了一個兩階段的庫存決策模型,但區別于前文關注的數量減少的情形,本文關注的是質量降低。產品質量的下降直接影響到產品的需求,這一點不同于數量損毀影響到產品的供給。通過建立動態規劃模型,我們逆向求解各銷售期的最優配給量決策、以及最優初始采購量決策,具體考察了庫存量、新鮮度水平和價格等參數變化對最優配給決策的影響,最后通過數值實驗對動態決策的庫存合并效果進行驗證,試圖為新鮮產品分銷商的跨季庫存管理工作提供有益的管理啟示。
2 模型描述
考慮一個經營季節性新鮮產品的分銷商。在產品采摘期,分銷商決策產品的初始庫存量Q;記單位采購成本為c。產品的銷售季可以劃分為n(n≥2)個周期(如圖1所示)。我們考慮一個完全競爭的市場,每期的產品價格pi(i=1,2,…,n)為外生參數,且為分銷商提前知曉。
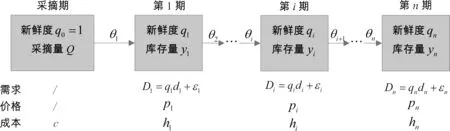
圖1 跨季銷售模型示意圖
銷售季中產品的質量隨著時間的推移而發生變化。我們引入“新鮮度”指標來刻畫產品的質量水平。借鑒肖勇波等[13]、Cai Xiaoqiang等[14]的做法,我們用[0,1]區間上的新鮮度指標來刻畫質量水平:新鮮度等于1意味著產品完全新鮮;新鮮度等于0意味著產品完全變質。記產品在采摘季的新鮮度為q0=1;第i周期初的新鮮度水平為qi∈[0,1],服從下列規律:
qi=θi×qi-1,i=1,2,…,n
其中,庫存保鮮因子θi是[0,1]區間上的隨機變量,表示庫存產品在第i周期的新鮮度相比于上一周期的保持程度。θi的具體分布取決于產品自身的變質特征;記其概率密度函數和累積概率分布函數分別為gi(x)和Gi(x)。
產品的新鮮度直接影響該期的市場需求。一般來說,產品新鮮度越低,市場需求越低。因此,我們假設第i期的市場需求Di滿足如下關系式:
Di=qidi+εi
其中常量di表示第i期對應于產品完全新鮮情形下的平均市場規模;εi為需求的隨機擾動項,記其概率密度函數和累積概率分布函數分別為fi(x)和Fi(x)。不失一般性,假設E[εi]=0。
銷售季中,隨著時間的推移,產品的庫存量也會發生變化(取決于前期的銷售情況)。記第i周期初的庫存量為yi。在第i周期初,在觀察到當前的剩余庫存量yi和新鮮度qi的前提下,分銷商需要確定當期從氣調庫中調配的產品數量(“配給量”),該決策等價于要確定保留到下一周期的庫存量zi(當期的配給量為yi-zi)。產品配給量確定以后,當期的市場需求Di實現,部分或者全部需求得以滿足(取決于實際需求與當期配給量的大小關系)。假設每增加一單位保留到下一周期的產品,分銷商需要支付hi的庫存持有成本。為簡化分析,假設每周期已經出庫、但是未銷售出去的產品殘值為零。分銷商希望通過合理決策各期的庫存配給量,實現自身期望利潤的最大化(假設他是風險中性的)。
3 最優決策及性質分析
分銷商面臨著一個兩階段決策問題:第一階段確定初始采購量Q;第二階段在每個銷售周期初動態確定預留給未來的庫存量(z1,z2,…,zn)。
3.1 最優庫存配給決策
我們采用動態規劃方法來解決分銷商的多周期庫存配給問題。在第i(=1,2,…,n)期期初,系統狀態可用三維向量(i,q,y)表示,其中q(∈[0,1])為當前的新鮮度水平,而y(∈[0,Q])為當前的庫存水平。記函數Vi(q,y)為分銷商在對應狀態下,通過最優庫存配給策略能夠在當前及后續銷售期內獲得的最大期望利潤。
對于最后一周期(即i=n),不管產品新鮮度如何,分銷商應該將所有產品出庫進行銷售,因此:
(1)
在中間周期,當已知第i+1(i=1,2,…,n-1)周期不同狀態對應的利潤函數的前提下,第i周期的庫存決策及其利潤函數由如下遞推方程式確定:
(2)
其中,
(3)
期望利潤函數的結構性質如引理1所示。
引理1:對任意周期i(=1,2,…,n-1)和期初狀態(q,y),函數Vi(q,y)和Ri(z|q,y)具有如下性質:
(a)Ri(z|q,y)是關于(y,z)的聯合凹函數;
(b)Vi(q,y)是關于y的凹函數。
證明:采用數學歸納法證明。首先在最后一周期,由利潤函數Vn(q,y)不難可得
因此,Vn(q,y)關于y凹。
(a) 假設Vi+1(q,y)是關于y的凹函數,可得
即函數Ri(z|q,y)的Hessian矩陣半負定。因此,Ri(z|q,y)關于(y,z)聯合凹。
(b) 返回公式(2),由(a)知其為目標函數是聯合凹函數、同時可行域是凸集的優化問題。根據凸規劃理論[15],可知Vi(q,y)是關于y的凹函數。
于是,利用數學歸納法,我們可將函數Vi(q,y)和Ri(z|q,y)的凹性推廣到所有周期i(=n-1,n-2,…,1)的情形。
由引理1可知,分銷商在每個周期初決策預留的庫存量時,面臨的是一個凹規劃問題。特別是,決策問題的可行域是凸集,因此周期i的最優配給量/預留量是唯一確定的,可由KKT條件進行求解,如定理1所示。
定理1第i(=1,2,…,n-1)周期初,給定分銷商的狀態(q,y),最優庫存預留量z*由如下方程組唯一確定:
(4)
其中,Φi(z)為Ri(z|q,y)關于z的一階導數,
(5)
λ1和λ2分別為對應于邊界條件z≥0和y-z≥0的對偶變量,λ1,λ2≥0。
推論1:在任意周期i(=1,2,…,n-1),給定期初新鮮度水平q,最優庫存保有量z*為期初可用庫存量y的單調非減函數。
證明:在對引理1的證明中,已證得Ri(z|q,y)函數關于(y,z)的交叉偏導是非負的,根據超模理論[16],當q給定時,可知Ri(z|q,y)在(y,z)上具有超模性(Supermodularity)。并且由于
可知z*關于y單調非減。
我們可以用收益管理的“邊際分析”方法對推論1進行直觀解釋。令
表示在周期i時分配z單位庫存給未來銷售時,每少分配1單位庫存(即多提供1單位庫存給當期市場銷售)能在該周期增加的期望邊際利潤;令
表示在同樣的基礎上,每多分配1單位庫存能在未來i+1~n周期內增加的期望邊際利潤。由此,公式(5)可以表示為:Φi(z)=Φ2(z)-Φ1(z),即未來期望邊際利潤與當前期望邊際利潤之差。分銷商通過比較這兩個期望邊際利潤來確定最優配給量:當分配一件產品給當前周期銷售的期望利潤超過將其保留給未來周期銷售所獲得的期望利潤時,就應該將產品供應給當前市場;反之,則留存產品給未來市場。可以看出,未來期望邊際利潤與當前庫存量無關,而當前期望邊際利潤是關于庫存量y的非增函數,意味著在其他參數給定的情況下,隨著y的增加,Φi(z)會變大/保持不變,分銷商在未來周期會獲取更優的期望邊際利潤,他應該提高/維持分配給后續周期的庫存量。
需要指出的是,當第i(=1,2,…,n-1)期初始庫存量y保持不變時,新鮮度水平q對最優配給量z*的影響并不具有類似的單調性。我們需要考察在y給定時,Ri(z|q,y)函數關于(z,q)的交叉偏導(見下式(6)),引理2幫助我們判定其符號方向。
(6)
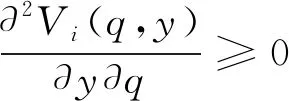
(1)當z*=0時,
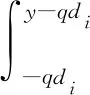
其關于(q,y)的交叉偏導:
(2)當z*=y時,
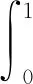
其關于(q,y)的交叉偏導為:
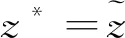
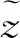
進一步有:
后面兩種情況可根據最后一期交叉偏導的符號方向由數學歸納法推導。由于
成立,因此綜上三種情況,可知第i期的最優值函數關于y和q的交叉偏導總是非負的。
令q1、q2(y)分別為以下方程式的唯一解:
(7)
(8)
定義函數p1(q|y)、p2(q|y)分別為:
p1(q|y)
(9)
p2(q|y)
(10)
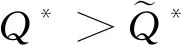
引理3:對于任意周期i(=1,2,…,n-1)及庫存量y(>0),總有q1≤q2(y)以及p1(q|y)≥p2(q|y)成立。
由公式(9)和(10)可知p1(q|y)≥p1(q|0)、p2(q|y)≤p2(q|0)。由于
p1(q|0)=p2(q|0)
因此p1(q|y)≥p2(q|y)成立。
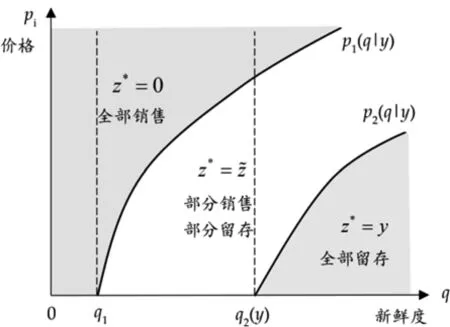
直觀上,q1表示在不分配產品給后續周期的情況下,未來期望邊際利潤為0時的新鮮度水平;q2(y)表示在分配y件產品到后續周期銷售的情況下,未來期望邊際利潤為0時的新鮮度水平。p1(q|y)、p2(q|y)可理解為給定期初庫存量y,在對應期初新鮮度水平q時,使分銷商的期望利潤分別在不給后續周期分配產品以及把所有產品都分配給后續周期銷售的情況下達到最優的價格閾值。定理2進一步給出了分銷商在不同參數條件下的最優配給策略選擇。
定理2若分銷商到達周期i(=1,2,…,n-1)時的既定狀態為(q,y),他所對應的策略選擇為:
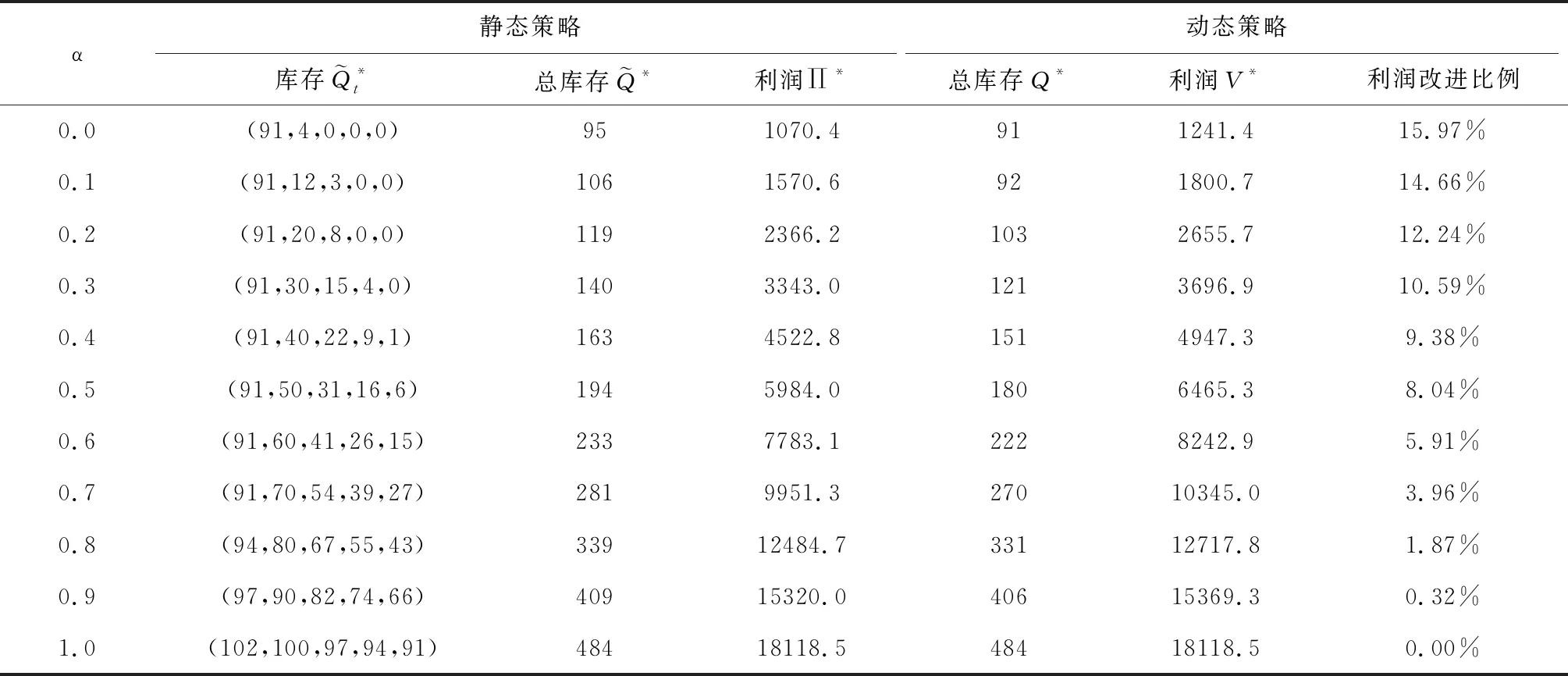
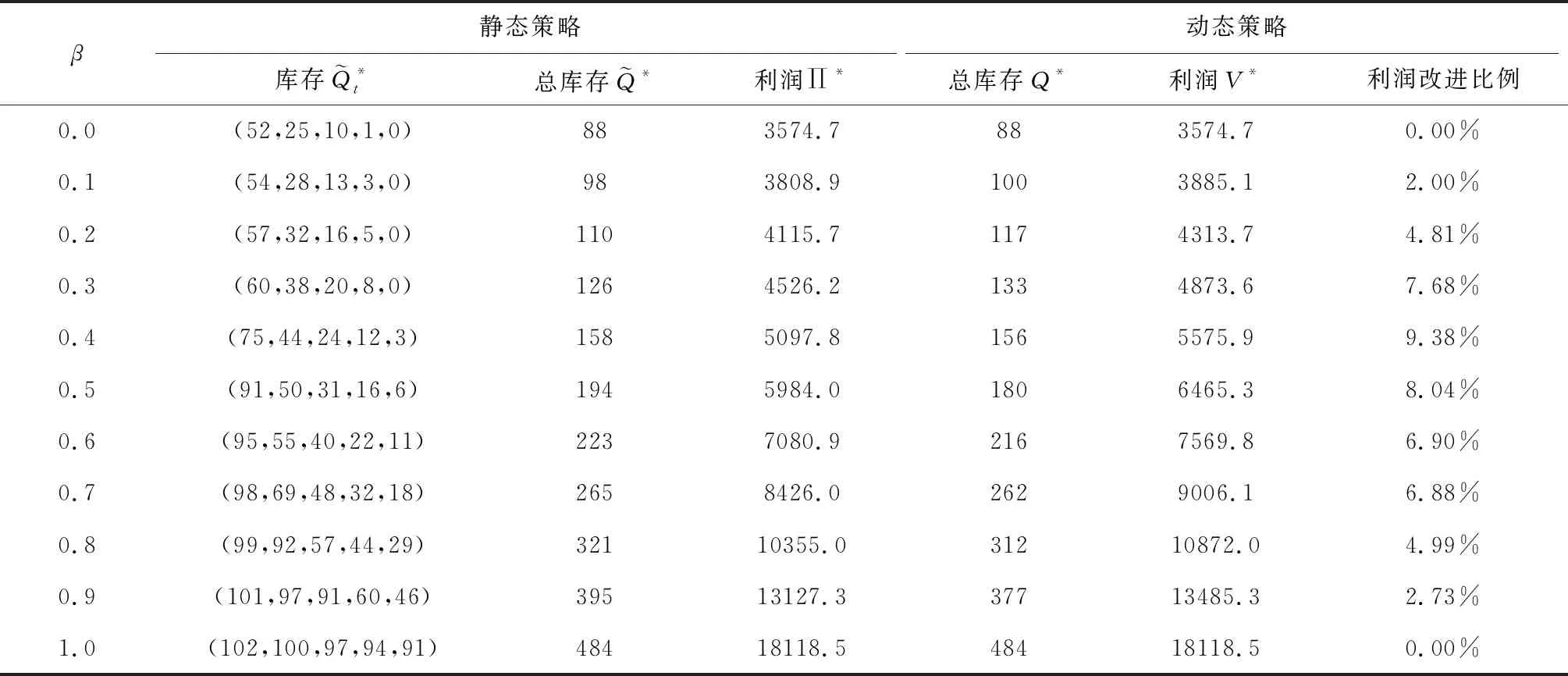
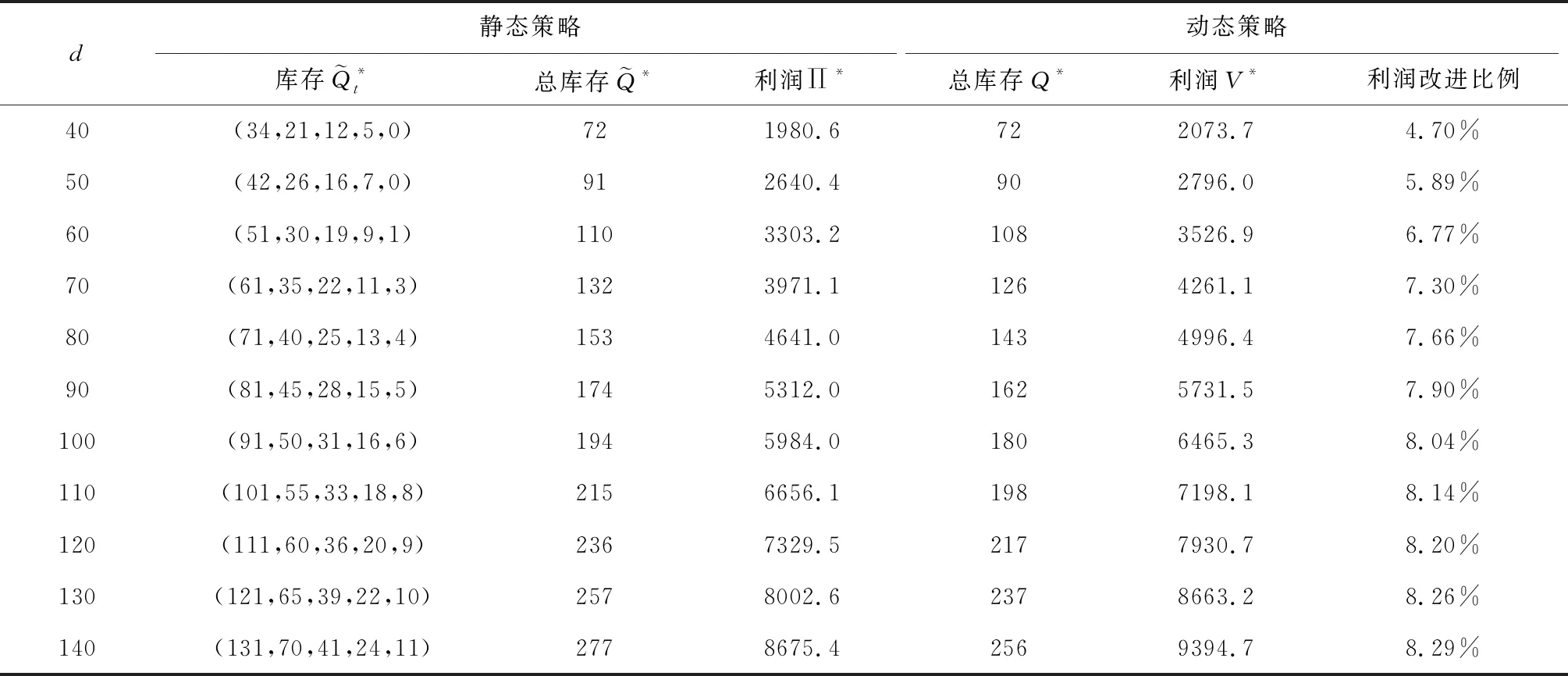
(a)當q (b)當q≥q2(y)且pi≤p2(q|y)時,分銷商應該將所有貨物都分配給未來周期銷售(z*=y); 證明:我們根據定理1 KKT條件所示的三種情形分別進行分析: (a)當λ1≥0且λ2=0時,Ri(z|q,y)在[0,y]上單調非增,在z*=0處取得最大值;此時需滿足: (11) 根據q1的定義,注意到當q 即pi≥p1(q|y),因此當q≥q1且pi≥p1(q|y)時,同樣有z*=0成立。 (b) 當λ1=0且λ2≥0時,Ri(z|q,y)在[0,y]上單調非減,在z*=y處取得最大值;此時需滿足: (12) 根據q2(y)的定義,注意到不等式(12)只有當q≥q2(y),即左邊≥0時,才有存在的前提。在此基礎上,可進一步將(12)整理為: 即pi≤p2(q|y),因此在q≥q2(y)且pi≤p2(q|y)時,z*=y能夠成立。 (13) (14) 當q1 由定理2可知,在新鮮度水平給定的情況下,周期i的期初庫存量越高,分銷商將傾向于分配更多的庫存在后續周期銷售;而在庫存水平給定的情況下,分銷商的配給量決策同時受到新鮮度水平和銷售價格的共同影響。根據引理3所揭示的各閾值之間的大小關系,我們可以將二維空間(q,pi)劃分為三個不同的區域,分別對應于分銷商在該期全部配給、部分配給還是不配給貨物的策略選擇,如圖2所示。 圖2 分銷商在第i期給定y時的最優配給策略選擇 分銷商在周期i確定當期的最優配給量時,除了考慮上述所討論的新鮮度水平、庫存量和價格等因素外,還需要考慮到分配給未來周期銷售的產品在儲藏過程中可能發生的變質因素。推論2說明了質量變質風險對最優配給量的影響。 推論2:對任意周期i(=1,2,…,n-1),在其他參數保持不變的情況下,庫存保鮮因子θi+1在隨機意義下越大,該期所對應的最優庫存配給量z*也越大。 推論2符合人們的直觀判斷,即產品越能保持新鮮,未來銷售所獲利潤就會越大,則應該分配更多的庫存在未來周期銷售。事實上,越來越多的分銷商選擇采用效果更好的保鮮手段來存儲產品,以提高產品在反季的市場競爭力。 在刻畫了多周期的最優庫存配給決策的基礎上,我們進一步對分銷商的最優初始采購量決策展開分析。 假設分銷商在采摘期訂購到的是完全新鮮的產品(即第一期的新鮮度水平q1=θ1),他需要確定最優的初始庫存量Q*,以使整個銷售期間的期望利潤最大化。記V(Q)為分銷商在初始采購量為Q以及對應的配給策略V1(q1,Q)下所能獲得的期望利潤,則有: V(Q)=E[V1(θ1,Q)]-cQ (15) 其中V1(q1,Q)對應于產品在銷售首期新鮮度降為θ1時,分銷商通過在當前及未來的所有銷售周期動態調整庫存決策所能獲得的最大期望利潤。 由引理1可知,V1(q1,Q)是關于Q的凹函數,易知V(Q)也是關于Q的凹函數。因此最優初始采購量決策Q*可以非常直觀地由一階條件獲得,如定理3所示。 定理3當利潤函數V1(q1,Q)為已知的前提下,分銷商的最優初始采購量決策Q*由如下方程唯一確定: (16) 由于函數V1(q1,Q)是由公式(1)所示的遞歸形式,難以得到Q*的顯性表達式,我們可以通過一些搜索算法來進行求解。 由于動態配給方法會追蹤產品在每個周期的新鮮度變化,并據此調整庫存決策,能更好地匹配有限的供給和不確定的需求,因此可以預見庫存合并效果的存在。我們以一個虛擬的靜態系統作為參照:分銷商在初始采購期就針對各期做好全部決策工作,即事先確定各期的庫存配給量,分開進行獨立管理。 (17) (18) 注意到在產品不發生變質的極端情況下,qi=1(i=1,2,…,n)總成立,模型的不確定性僅體現在各周期的需求擾動項上,由于假設εi為獨立同分布的隨機變量,因此庫存配給模型退化為簡單的n個獨立的庫存采購模型,此時采用靜態的報童模型方法求解得到的結果與最優的動態結果等價。 為體現動態策略在多周期問題中的突出優勢,我們考慮n=5的情形,同時為簡化計算,我們假設庫存保鮮因子θi(i=1,2,…,n)服從一個離散分布: 其中,α(∈[0,1])為θi的較低取值,β∈[0,1]表示θi取值1的概率,即產品在第i周期以β的概率不繼續變質,以1-β的概率變質且新鮮度降為上一周期新鮮度的α比例。為提高計算效率,我們沒有采用求積分的方式計算每期需求的期望值,而是通過隨機生成N=2000個服從均值為0、標準差為σ的正態分布的隨機數,來模擬εi的實現值,從而用樣本平均值代替總體期望值。為減少計算量,產品采購量和留存量將只取整數值。 基礎組的實驗參數按如下設置: 庫存保鮮因子θi(i=1~5)的較低取值α=0.5; 庫存保鮮因子θi(i=1~5)取值1的概率β=0.5; 各期對應完全新鮮產品的需求量 di=100(i=1~5); 各期需求擾動因子εi(i=1~5)的標準差σ=10; 單位采購成本c=40; 各期單位產品價格pi=100(i=1~5); 保鮮期單位產品儲藏成本hi=10(i=1~4)。 在第一組實驗中,我們考察保鮮因子的較低取值α的變動所帶來的影響。α越小,說明庫存保鮮因子的方差越大,即產品在隨機意義下,越容易變質。我們計算了在α在[0,1]上的不同取值下,靜態系統和動態系統的最優總采購量及對應的最優期望利潤,如表1所示。 表1 庫存保鮮因子取值分布對績效的影響 表1的最后一列顯示了分銷商采用動態庫存配給策略所獲得的最優期望利潤,相比采用靜態配給策略多出的比例。可以看出,動態策略總是能夠在總采購量低于靜態總采購量的情況下,取得比靜態總期望利潤更好的表現,并且動態策略的這種庫存風險合并效果隨變質風險的加大而更加顯著,極端情況下(產品有一半的概率完全變質),利潤的改進比例達到15.97%。 在第二組實驗中,我們保持基礎組的其他實驗參數不變,改變保鮮因子取值1時的概率β(β越接近0.5,庫存保鮮因子的方差會越大,表明變質的不確定性越高)。實驗結果如表2所示。 以上兩組實驗共同說明了產品變質的風險越大(即庫存保鮮因子的方差越大),動態配給策略的利潤改進效果越為顯著,這與前人研究中產品的變質特性會直接影響到庫存風險合并效果大小的論述一致。 在第三組實驗中,我們保持基礎組的其他實驗參數不變,改變各期市場規模d的大小。實驗結果如表3所示,隨著d的不斷增大,采購量和供應給跨季市場的產品數量不斷增加,動態系統相比靜態系統最優期望利潤的改進比例也呈增長的趨勢。當市場對完全新鮮產品的確定性需求數量達到140個單位/期時,利潤改進比例達到8.29%,我們可以合理預見隨著d的增加,利潤改進比例還將提高,但增幅會越來越有限。 表2 庫存保鮮因子概率分布對績效的影響 表3 市場規模對績效的影響 從ε的角度考察需求波動性影響的第四組實驗結果如表4所示。隨著標準差σ的增加,總采購量不斷降低,供應給跨季市場銷售的產品數量也在不斷減少,并且動態系統的利潤改進比例也呈現出不斷減小的趨勢。當市場上不存在隨機擾動時,需求完全由產品新鮮度和市場規模決定,動態策略的改進比例達到最高的8.7%。 兩組實驗結果表明由d和ε造成的需求波動性,對動態策略的庫存風險合并效果具有同樣的影響,即需求的不確定性越低,來自市場的風險越小,動態策略的優化效果會更加顯著。 本文考慮新鮮產品的分銷商在應季采購一定數量的庫存留待后續季節銷售的問題。我們將其分解為一個兩階段的庫存決策問題并采用動態規劃方法進行分析,證明了每個周期的最優配給量是唯一確定的,可用KKT條件進行求解。進一步地,我們指出在其他參數保持不變的情況下,當期初庫存水平越大、期初價格越低、期初新鮮度越高以及下期的變質風險越低時,留存給未來銷售周期的庫存量應該越多。數值實驗結果還表明當產品變質風險更大、需求不確定性更低時,動態庫存配給策略能夠為分銷商帶來更加顯著的利潤改進效果。 表4 需求擾動項對績效的影響 新鮮產品的變質特性和跨季市場的風險因素加大了經銷商的盈利難度,給他們的庫存管理帶來了極大的挑戰。另外,產品無法在跨季市場上補貨以及因質量降低而加劇的需求不確定性因素,使得這一問題相比一般的多周期庫存問題具有不一樣的供需匹配的難點。采用動態配給策略,對同時面臨著供應受限和需求不確定的變質產品進行庫存管理,是獲得利潤最大化的有效方式,具有廣闊的研究前景。我們的工作還可以從以下幾個方面進行拓展:(1)引入新鮮度的需求敏感系數,考慮更為一般的非線性關系的情形;(2)將模型擴展為同時考慮保鮮投資和庫存配給的多周期聯合決策的問題;(3)納入新鮮產品供應鏈上其他相關利益主體的優化問題展開研究。
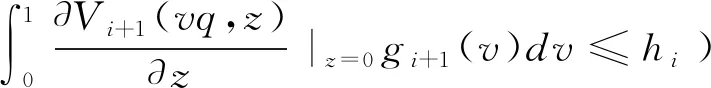
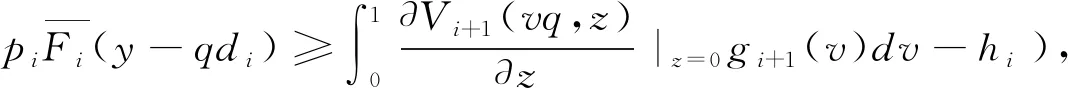
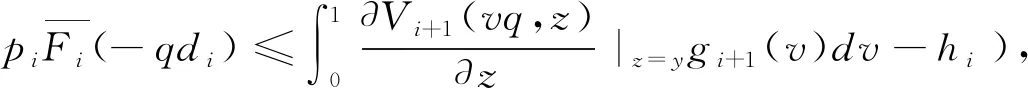
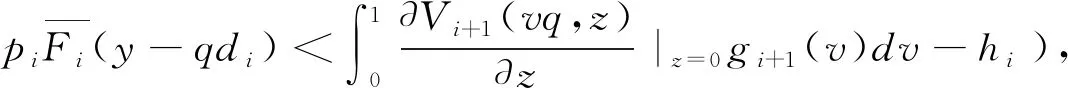

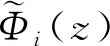
3.2 最優初始采購量決策
4 靜態配給及采購量決策
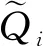
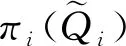
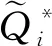
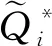
5 數值實驗
5.1 產品變質性的影響
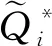
5.2 需求波動性的影響
6 結語