再入飛行器滑翔段精確減速控制技術*
范世鵬 王 亮 賈靜雅 李 伶 劉曉東
1.北京航天自動研究所,北京100854 2. 首都航天機械公司,北京 100076
為滿足復雜的現代戰爭需求,再入飛行器必須滿足多種終端約束條件。制導技術的內涵不僅僅停留在命中精度層面,還要將終端速度控制在指定的范圍內,以創造良好的末端探測條件。例如,潘興II彈頭必須減小彈道末端的飛行速度,以免被嚴重的氣動加熱所產生的等離子體形成信號屏障,導致彈上雷達無法正常工作[1]。
氣動減速是在制導指令中疊加額外的附加攻角,利用氣動阻力進行減速,是工程上常用的一種有效方法。同時,產生的有界振蕩指令在一定程度上可以提高導彈突防的能力[2]。連葆華等采用變結構控制方法,對速度進行控制[3]。但這種減速方法沒有充分地利用彈上加速度信息,對速度的控制精度較差。
周荻等為實現導彈突防,將正弦指令作為參考輸入,并推導得到一種滑模制導律,使導彈在機動突防后仍可以精準命中目標[4]。Xue等研究了再入飛行器的預測校正制導,實質上是通過全程的高度剖面實現對速度的控制,但該算法的計算量相對較大[5]。劉鵬云等以錐形減速滿足火箭彈對終端速度的要求,但所設計虛擬目標的運動規律可能因火箭彈阻力特性而無法實現[6]。李強和陳思遠等提出一種大氣預估的方法,以正弦規律的側向附加機動控制速度,同時以最優制導律保證落點和落角約束,但需要根據當前狀態在線預測終端速度,會增加彈上計算量[7-8]。陳安宏等以側向機動實現減速,解決了平飛段速度控制問題[9],然而,實際工程很少采用平飛,而以特定彈道傾角的滑翔飛行。王潔瑤等在合理的假設下,推導了準平衡滑翔段的彈道近似解,具有很好的參考價值,但未給出速度的解析公式[10]。
本文針對再入飛行器滑翔段減速控制問題,充分利用速度、阻力加速度等導航與測量信息,提出一種氣動精準減速的可行方法。首先,考慮重力的影響,修正了滑翔段理想速度關于高度的解析表達式;其次,分析了減速回路與傳統制導回路之間的關系,提出一種減速回路設計方法,針對2個回路耦合的特點,提出相應的控制策略。
1 理想速度解析表達式
為便于研究,常將空氣密度視為飛行高度的雙參數指數函數:
ρ=ρ0e-h/hs
(1)
其中,ρ0=1.752;hs=6.7×103。
圖1對比了標準的大氣密度與擬合高度-密度公式;圖2給出了大氣密度擬合的絕對誤差和相對誤差。
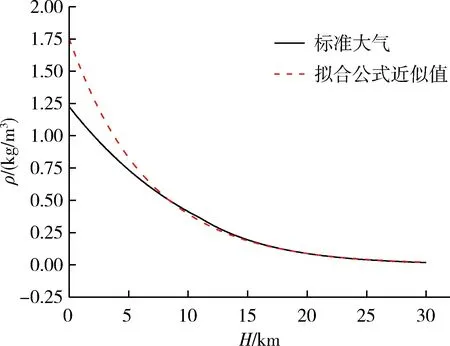
圖1 擬合公式得到的大氣密度近似值與實際值
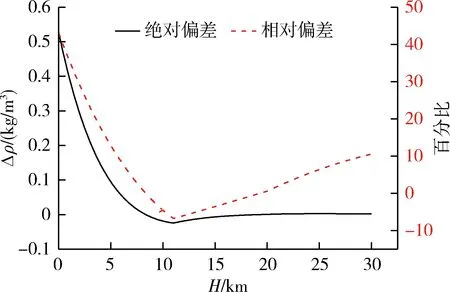
圖2 擬合公式近似的相對誤差與絕對誤差
根據以上分析,在高度5km~25km的大氣擬合精度絕對偏差和相對偏差均較小,同時,適宜飛行器實現滑翔飛行。
在數學模型中,關于速度和高度相應的微分方程可表示為:
(2)
其中,m為質量;V為飛行速度;h為飛行高度;Cx為平衡滑翔攻角對應的氣動阻力系數;ρ0為空氣密度;S為參考面積;g為重力加速度;θ為彈道傾角。
對于平衡滑翔彈道,可將彈道傾角視為常值。且平衡攻角為常值,因此,將Cx視為常數。用式(2-1)除以式(2-2),可得H-V空間的微分方程為:
(3)
可以看出,上述微分方程為伯努利方程的形式,可變形為:
(4)
變量代換w=V2,則:
(5)
若終端速度為Vf,則通過求解上述微分方程可得,高度在h到hT區間內:
(6)
其中,K可視為常值,其表達式為:
(7)
假設彈頭無阻力,則K=0,代入上式可得:
(8)
可以看出,上式為機械能守恒定律。若忽略重力的影響,設g=0,則上式變為:
V(h)=VfeK(e-hT/hs-e-h/hs)
(9)
式(8)為傳統錐形減速所采用的理想速度解析表達式。
由于滑翔段飛行時間較長,重力影響較大,因此,理想速度的推導必須考慮重力因素的作用。由于式(6)中關于重力項無法解析求解,對該項采用高精度的多項式逼近。
由麥克勞林公式可知,
(10)
其中,N取正整數。由式(9)可知,若x/N趨近于0時,則截斷誤差接近于0,即N的取值應根據x來確定。一般的,x/N<0.1。
為方便推導,記:
μT=e-hT/hs,μ(h)=e-h/hs
(11)
利用式(9)處理式(6)中的重力項,可得:
(12)
將式(11)中多項式展開后積分,可得:
(13)
則考慮重力的理想速度表達式為:
(14)
2 減速控制技術
這里將為保證落點、落角等終端約束而形成的制導回路稱為傳統制導回路,制導律可采用彈道成型等一類最優制導律,在此不做深入研究。由于減速控制回路與傳統制導回路都是通過產生攻角來消除控制偏差,記ηc0,ηc1,ηc和η分別為傳統制導回路合攻角指令、減速回路合攻角指令、最終的合攻角指令和彈體合攻角響應,則2個回路的耦合關系如圖3所示:
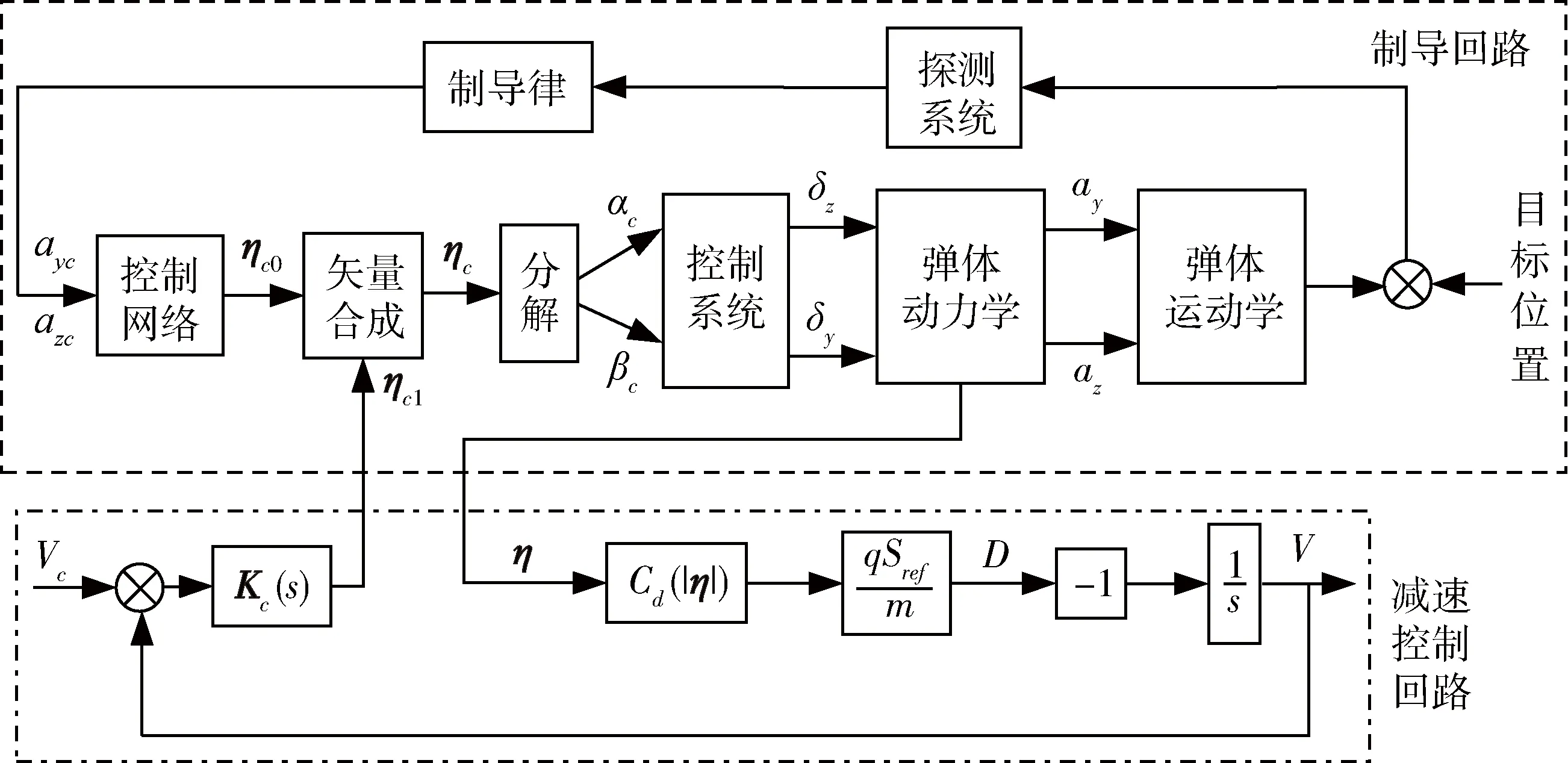
圖3 制導與控制系統框圖
記阻力系數為Cd,減速回路控制器Kc可設計為關于速度跟蹤誤差比例-積分-微分的PID形式,為加快跟蹤回路的響應速度,省略積分項而采用比例-微分PD形式:
ηc1=K(Vn-Vc)+KD(Dc-Dm)
(15)
其中,Kv和KD分別為比例項和微分項的增益,Vn和Dm分別為速度導航值、阻力加速度測量值,Dc為當前期望阻力加速度,由下式求得:
(16)

可采用零極點配置來獲得Kv和KD,考慮到速度的慣性較大,而攻角為快周期變量,因此,設計減速回路增益時,可忽略攻角響應的動態過程,則此時減速回路的特征方程為:
s2+KvCdSref/ms+KDCdqSref/m=0
(17)
同時,減速回路增加一個零點,P0=-KD/Kv,可用于調節動態特性。
鑒于主要的未建模環節(彈體動力學)頻率一般為20rad/s左右,而速度的慣性較大,可將速度控制回路的特征頻率配置在5~10rad/s,阻尼大于0.8。由根軌跡重心不變原理,彈體動力學對應的極點右移量小于10rad/s。所有極點均位于左半平面,從而保證控制系統的收斂性。
顯然,若傳統制導回路的合攻角指令不小于減速回路合攻角指令時,前者為保證落點、落角精度而進行機動飛行,已經達到了當前時刻減速的要求,無需生成減速回路的附加指令,此時采取“沿用傳統制導指令作為最終的指令”的策略,即ηc=ηc0。
若傳統制導回路的合攻角指令小于減速回路合攻角指令時,則需要在垂直于ηc0的垂直方向上疊加一個合攻角指令Δηc,使最終的合攻角指令為|ηc|=|ηc1|,則分解到俯仰和偏航通道的攻角與側滑角指令分別為:
(18)
圖4給出了上述情形下的2個回路合攻角指令關系的示意圖。
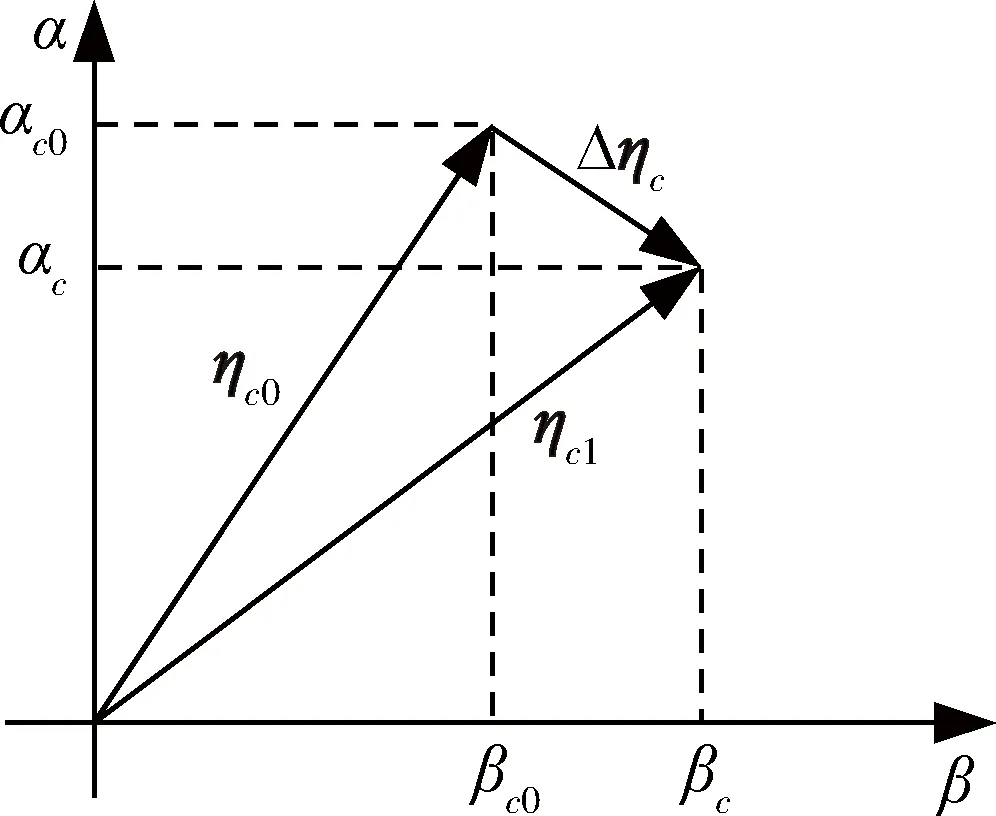
圖4 控制指令合成示意圖
對于傳統制導回路而言,減速回路所產生的附加攻角指令是一種干擾,將造成彈目運動位置、速度的偏差。由于制導回路將逐漸主動消除偏差,因而會形成合攻角在空間的錐形運動。
3 仿真驗證
采用六自由度非線性模型進行數學仿真驗證,飛行器數學模型采用最大升阻比為1.5的氣動布局。初始高度為27000m,初始彈道傾角為-10°,初始速度為2220m/s,在25~5km范圍內引入錐形減速回路,要求落點精度優于10m,期望落速為550m/s±100m/s,傳統制導回路采用彈道成型。圖5~8給出了在引入和未引入減速回路2種條件下的彈道重要變量仿真結果。

圖5 V-H空間的實際速度與理想速度
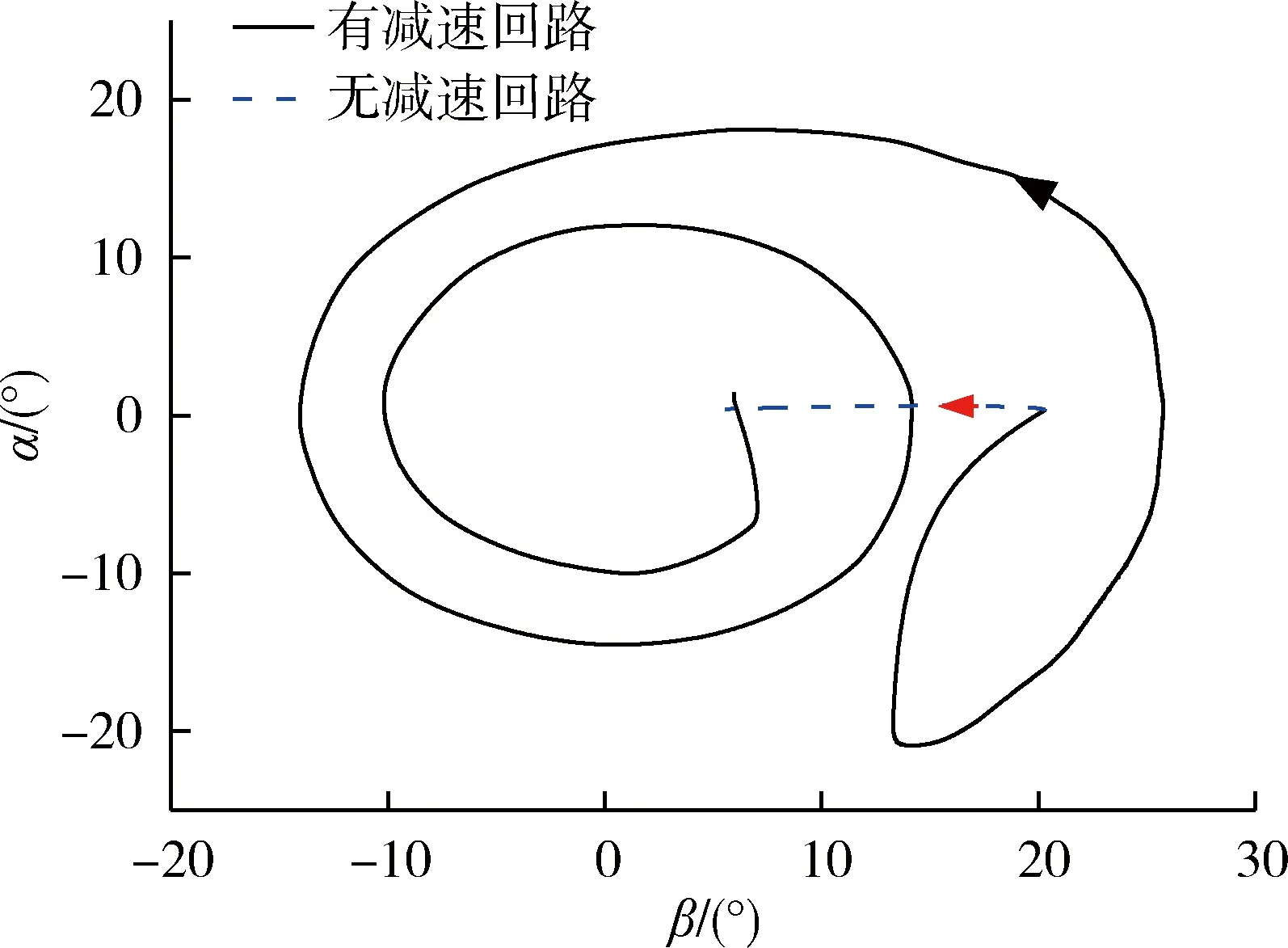
圖6 減速段攻角與側滑角的相軌跡
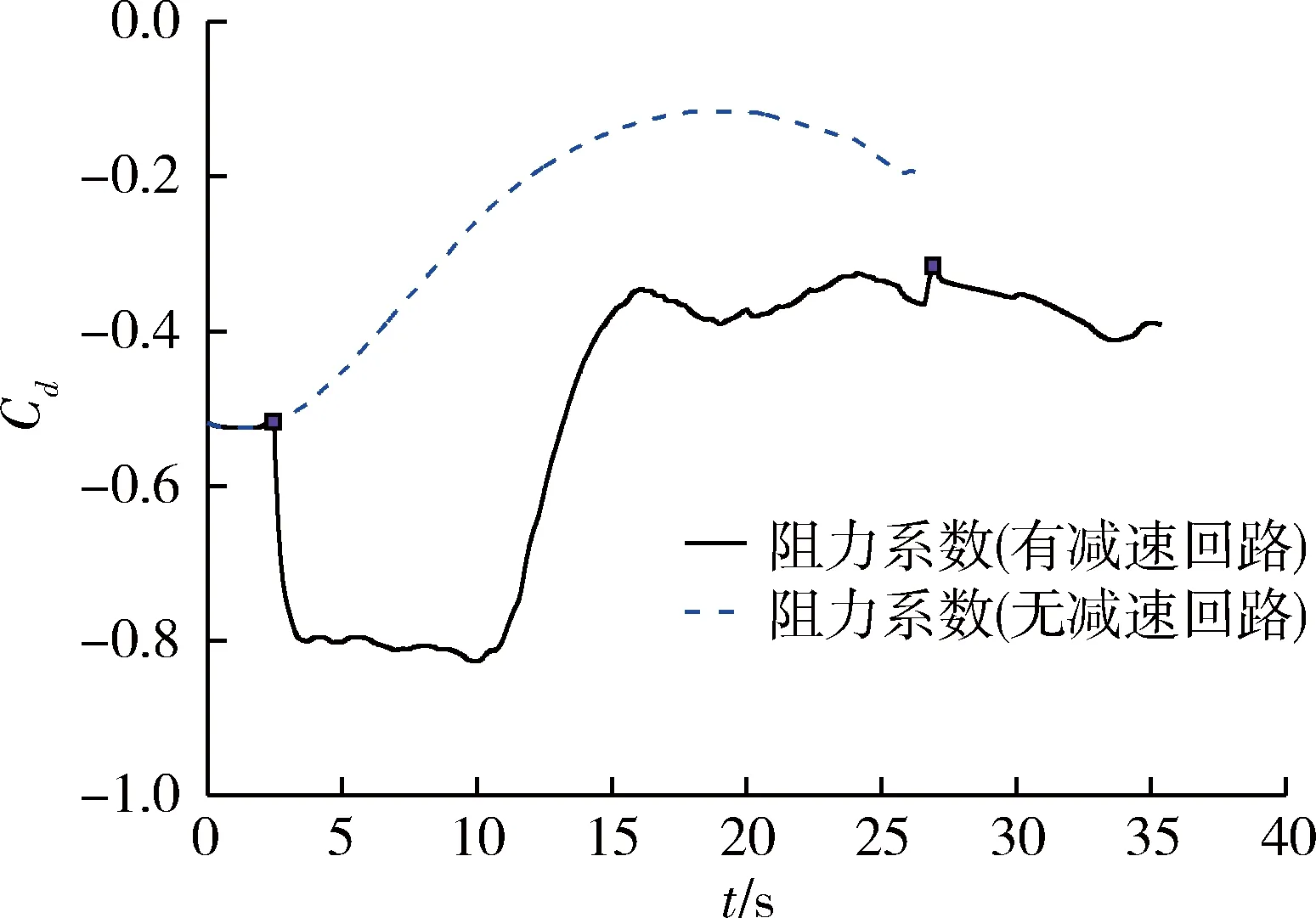
圖7 阻力系數Cd曲線
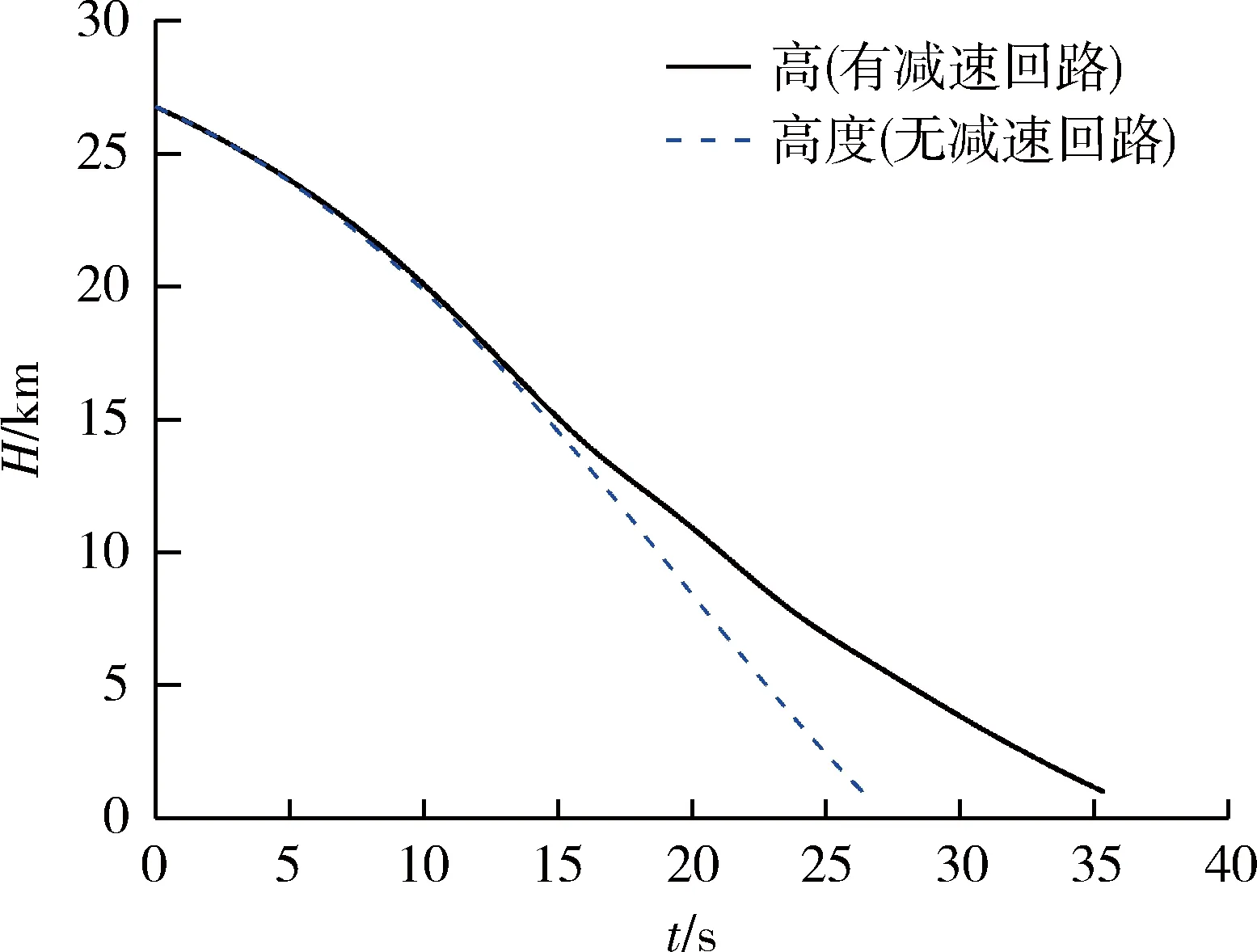
圖8 高度H曲線
從仿真結果可以看出,當引入減速回路后,飛行時間變長,通過攻角與側滑角交替錐形運動,使飛行過程中氣動阻力系數增大,從而使終端速度滿足要求。在滑翔段25km降至5km的過程中,在引入和不引入減速回路2種條件下,減速回路對速度剖面進行了大幅度的調整,兩者的終端速度分別為552m/s和1128m/s,由此可見,通過氣動減速是一種有效的速度控制手段。
4 結論
隨著再入飛行器控制技術的不斷發展,滿足終端速度、位置及攻擊角度等要求的多約束制導方法始終是該領域的關鍵技術。本文根據滑翔段的特點,在合理假設下,以高度為自變量的滑翔段速度運動規律具有解析形式,同時由于飛行器導航系統可以獲取高度信息,這種方法適用于實際工程中的速度控制。由于傳統制導回路與減速控制回路相互影響,本文在設計減速回路控制律的同時,制定了有效的控制策略,在不影響打擊精度的前提下,實現了終端速度的精準調節。

