基于混合算法的數字高程模型及數據結構構建

文/葉果

1 引言

數字高程模型是以數字形式描述的地形表面模型，在模擬攝影測量和分析攝影測量中，地面上的信息（地形，特征和不同的名稱）通過圖像和注釋（如輪廓線，地貌符號）顯示在圖紙上。函數的特征由不同的符號和文本注釋表示。這種地形圖很常用。按照一定的結構組織觀察數據，以建立數據模型的表達，最后的數據管理和重建由計算機實現，并在允許的響應時間內精確渲染3D 地形。

在最常見的形式中，平面和波紋數據構成數字地面模型，并且還包括從其獲得的數據，例如斜率，縱橫比，視線等。視覺景觀不僅具有表達表達的形式，而且還具有數據規模。但是，詳細數據和地形水平的數量彼此密切相關。如何實現兩者之間的最佳平衡成為研究的重點。優點是手動使用相對直觀方便，但其缺點也很明顯，即管理不方便，特別是不能直接用于計算機。因此無法滿足各種技術的自動化要求。因此，數字產品逐漸取代傳統的地圖，其中，數字地圖和數字地形模型為典型的產品。數字地面模型（DTM）已成為空間信息系統的組成部分。因此，系統地為大面積創建數字高程模型已成為當務之急。

2 數字高程模型的構建算法

數字高程模型被定義為一系列高程值，表示以數字形式存儲的對象的位置，并且是表示區域中的地形的有限系列的三維向量。獲取正確的數據是構建DEM 的第一步，也是最重要的一步，它不僅會對DEM 的準確性具有直接影響，還直接影響成本。從數據源和采集方法來看，包括：地面直接測量，如GPS，現場測量等。與傳統地圖相比，DTM（DEM）在信息數字表達上，具有具有無可比擬的優勢。首先，它可以直接輸入計算機，用于各種計算機輔助設計系統。其次，對于大量信息的存儲，可以使用DTM 多層數據結構功能，包括可以包含和表達非垂直排列的功能的地形圖。

需要快速找到起點所在的三角形，因為這是提高有限插入效率的重要部分，且這些插入直接影響算法的輸出效率。其中，算法在確定三角形中，還具有以下的關系定義：設V，K 為兩個三角形端點，V 為插值點。則點和線之間的關系是：

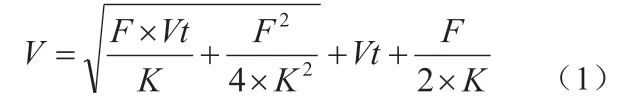
在TIN 中，如若對三角形之間的拓撲關系加以建立，則很容易根據三角形和三角形區域坐標之間的拓撲關系來評估具有插入點的三角形。如果給出點d（x，Y），則區域坐標定義為：

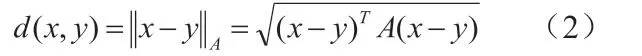
線段和三角形的交點可以減小以使線段與線段相交。如果兩個端點為如果第一線段位于第二線段的兩側并且第二線段的兩個端點也位于第一線段的兩側，那么則說明這兩個段相交。離散數字高度模型通常直接從地球表面測量原始或無組織數據。采樣點通常具有分布不規則特征的地形特征。通過使用某些項，可以創建具有獨特特征的表面。

3 DEM與TIN的數據結構

TIN 既可以由矢量方式構建,也可以由柵格方式構建。對于具有隨機離散點的不規則三角剖分的構造，基本思想是根據隨機分布的原始高光創建一個連續覆蓋整個研究區域的不規則三角網絡TIN。如果三角剖分中沒有約束數據，那么可生成的數字土壤模型就不能正確表達表面的復雜關系，與此同時，也不能滿足實際應用的需要。因此，在隨意數據三角測量中包含限制線成為一個關鍵問題。然而，地球表面的形狀實際上是一個不規則的表面，而不是一系列簡單的表面，特別是在三角形網格點稀少且地形變化很大的破碎地形上，平面插值的使用必然導致擬合表面的顯著變形。

建立的整體插值模型是根據研究區域內所有采樣點的觀測結果確定的。因此通常用于模擬廣泛的宏觀趨勢。使用矩陣，只要原點的地理坐標，網格間距和矩陣的行和列信息，就可以得到當前站點上每個區域的地理信息。建立每個區域之間的拓撲關系。也就是說，找到每個三角形與其他三角形的公共邊界，并按順序將其保存為文件。此外，我們同意所有跨越限制邊緣的三角形被設置為成為限制邊緣的影響域，并且影響域的每個三角形邊緣變為對角線。在地形中，與其所在三角形的三個角點有關的插值點的插值，在該區域中幾個采樣點的高階函數上顯得更合理。

假若采用一般上通用的多項式，便可以對更復雜的曲面加以創建。分析多項式的前三個項（兩個二次項和一個零項）并發現它們可以生成一個平面。通常，選擇三角形作為形成地面的表面，因為三角形表面是確定性的。將TIN 數據中的每個三角形劃分為基于重心的三個子三角形。目標是將三角形劃分為三個區域，并使用每個區域找到子三角形，其中每個區域的公共邊緣具有不同的三角形。嵌入約束線段（屬性線或約束線段）時，需要知道哪些三角形與約束線段相交，以及三角測量中的哪些邊與約束線段相交，然后執行局部三角測量重建和LOP（部分優化過程）優化。

4 結論

對于DEM 構造方法，本文采用T1N 和規則網格兩種建模方法實現DEM 構造，并討論了包含TIN 的算法并確定了相應模型。介紹了普通網格（DEM）模型的快速構建和小波簡化方法，之后總結了計算機上顯示的三維圖像的基本知識。此外，全局控制矩陣索引的存儲結構是用于該混合模型的局部三角剖分，它解決了大規模數據的精確三維地形映射。常規網格是DEM 和不規則三角測量TIN 以及兩者的混合應用。