電子束氨法脫硫反應器內部劑量率的模擬計算
王棋赟 李建軍 李升華
(1.四川大學建筑與環境學院, 成都, 610065;2.國家電投集團遠達環保工程有限公司, 重慶, 4011222)
電子束氨法脫硫(EA-FGD)是一種等離子體煙氣處理技術,基本原理是利用高能電子束轟擊鍋爐煙氣生成的OH、O3等強氧化性產物將煙氣中的SO2和NOn氧化,繼而與H2O和NH3反應生成(NH4)2SO4或NH4NO3的過程。電子束氨法脫硫的主工藝系統是煙氣輻照處理系統,它由電子加速器和反應器組成。系統運行時,反應器內電子束呈一個幾何輪廓為扁平狀四棱錐簾狀射束。
鑒于源的不規整特性,加之EGS4在處理粒子輸運問題上更為靈活、涉及物理過程也更全面[1],過去在EA-FGD反應器設計時通常采用EGS4程序進行模擬計算。然而EGS4程序運行前,需要用戶用高級計算機編程語言構建粒子輸運的空間環境等諸多信息,這對設計人員編程能力提出了較高的要求。MCNP與EGS4同屬于蒙特卡羅方法的分支,比之EGS4,MCNP通過定義曲面來構建空間體,且不需要像EGS4那樣描述粒子穿透不同區域的形式,也不需要用戶自行編寫代碼生成偽隨機數;在解決了MCNP對不規整源的描述困難后,如能驗證MCNP程序計算結果誤差在可接受范圍內,則可以在今后類似設計中,一定程度上降低設計的難度。
本文利用“小孔成像”原理來解決MCNP對不規整源的描述困難。通過模擬文獻[2]的試驗場景,將結果與試驗值進行比較,驗證MCNP用于電子束氨法脫硫反應器內部劑量率計算的可行性。
1 模型建立
試驗電子束氨法脫硫煙氣輻照處理系統,裝置采用碳鋼反應器[2],反應器尺寸為〔140 cm(內徑)×200 cm(長)〕,鈦窗尺寸為(100 cm×50 cm×0.003 cm),兩層鈦窗之間間距為7 cm,電子束流偏轉點到下層鈦窗上表面距離為130 cm(如圖1)。此外,電子束能量為0.57 MeV,束流強度是5 mA,輻照時間為30 s。
利用“小孔成像”原理模擬電子束氨法脫硫裝置加速器引出窗[3]出射的電子束,即在MCNP源柵元描述時將此抽象成一個位于“圓筒”內部的粒子源,而在圓筒的底面存在一個“矩形孔”,長寬比例與鈦窗相同,如圖2所示。
通過將除“矩形孔”外的圓筒柵元的重要性設置為零,即可對這些點源發射的“多余”粒子不進行跟蹤,但利用“小孔成像”建立的源會因這些“多余”的粒子引入一個幾何修正因子η,將實際粒子數進行一定程度的“放大”,以抵消那些多余的粒子。該值可以通過把矩形孔設置成探測柵元,記錄矩形孔中的粒子通量反算得出。關于軔致輻射,因為在入射電子能量為幾個兆電子伏時,其能量損失方式是以電離能量損失為主。兩者之比為[4]:
(1)

圖1 反應器束流廓面示意圖
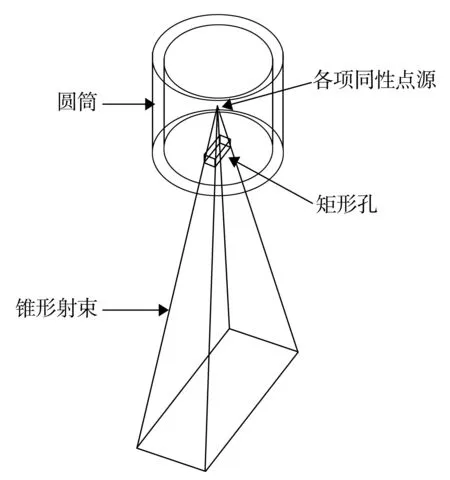
圖2 棱錐射束引出示意圖
式中,(-dE/dx)r為單位路程輻射能量損失;(-dE/dx)e為電離能量損失;Z為介質原子序數;E為電子束能量,MeV。
文獻[2]的試驗是在空氣介質中進行的,以氧原子的序數計算,可知當入射電子能量為0.57 MeV時,軔致輻射與電離輻射能量損失之比為0.57%。因此,在計算反應器內部劑量場時,可以忽略軔致輻射的影響。
2 計算過程與結果
試驗采用的木架模型,通過兩次更換木架的方向分別測量3個方向的劑量場,即反應器剖面劑量場、反應器隨電子入射深度方向的劑量場和反應器中心截面的劑量場[2],試驗方案示意圖3。
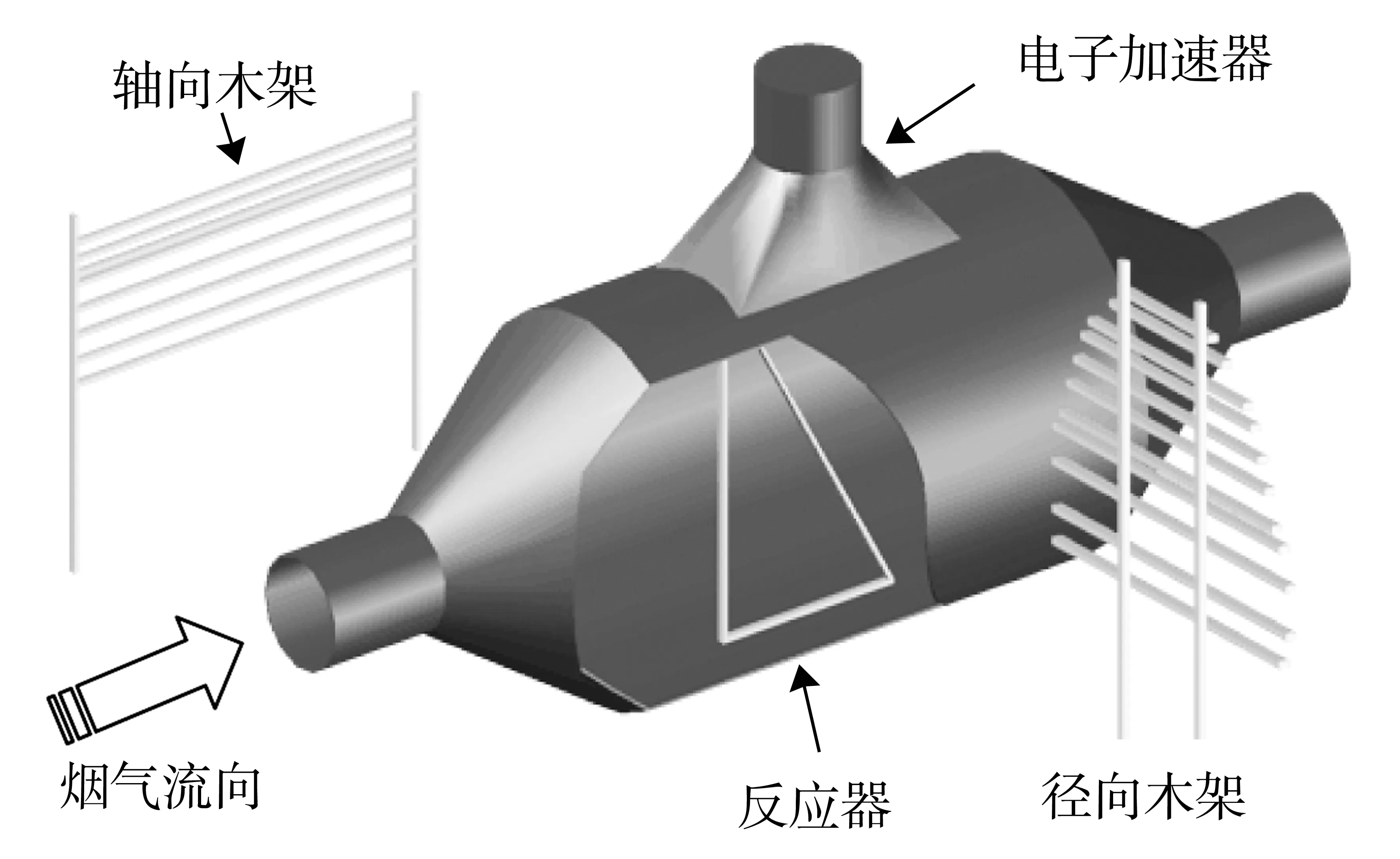
圖3 試驗方案示意圖
文獻[2]中未介紹木架的尺寸大小及木料密度,考慮過于細長的方木可能因為自重而彎曲變形,故驗證過程暫按方木尺寸2 cm×1 cm考慮,密度按0.4 g/cm3計。計算時,MCNP抽樣粒子數為1×108,用F4卡計數,計數柵元體積為8 cm3,結果標準差均滿足統計檢驗(σ<0.1)。
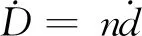
(2)
其中,

以剖面試驗中木架上第一排中點處劑量率計算為例,其劑量率與30 s累積劑量計算結果為:
式中,D為累積時間內的吸收劑量,kGy;t為積累時間,s。
MCNP計算中所使用的劑量乘子卡點值函數DE-DF系數(即通量-劑量轉化系數f)可通過《輻射劑量學》[5]中給出的電子質量碰撞本領計算求得,如能量為0.6 MeV的單能電子對應的質量碰撞本領s/ρ=1.743 MeV·cm2/g,則可計算得出轉換系數:
綜上,可得到反應器剖面劑量場(示于圖4),圖5給出了實測的反應器剖面劑量場。
由圖4知,因木架(截面尺寸2 cm×1 cm)的屏蔽散射作用而導致的對劑量場的影響效應:木架使反應器內劑量場出現一個“陡降區”,在木架下方,劑量場有所回升,形成一個類似“山坳”的劑量場區間,而這一現象是圖5實測劑量場所沒有的,圖5左上區域等劑量線內凹,可能就是木架左端采用木料根部,密度比右側更高的原因所導致的。為此,將木架截面尺寸修改為1 cm×0.5 cm重復計算,然則,這種“山坳效應”仍然存在。
文獻[6,7]用EGS4對該實驗進行了模擬,模擬過程忽略了木架的影響,設置抽樣粒子數為1×106,可得到滿足統計學檢驗的計算結果(σ<1%)。為與之對比,在MCNP建模過程中刪除木架柵元,忽略木架的影響,將計算結果分別與文獻[2,6,7]的結果進行比較(表1)。
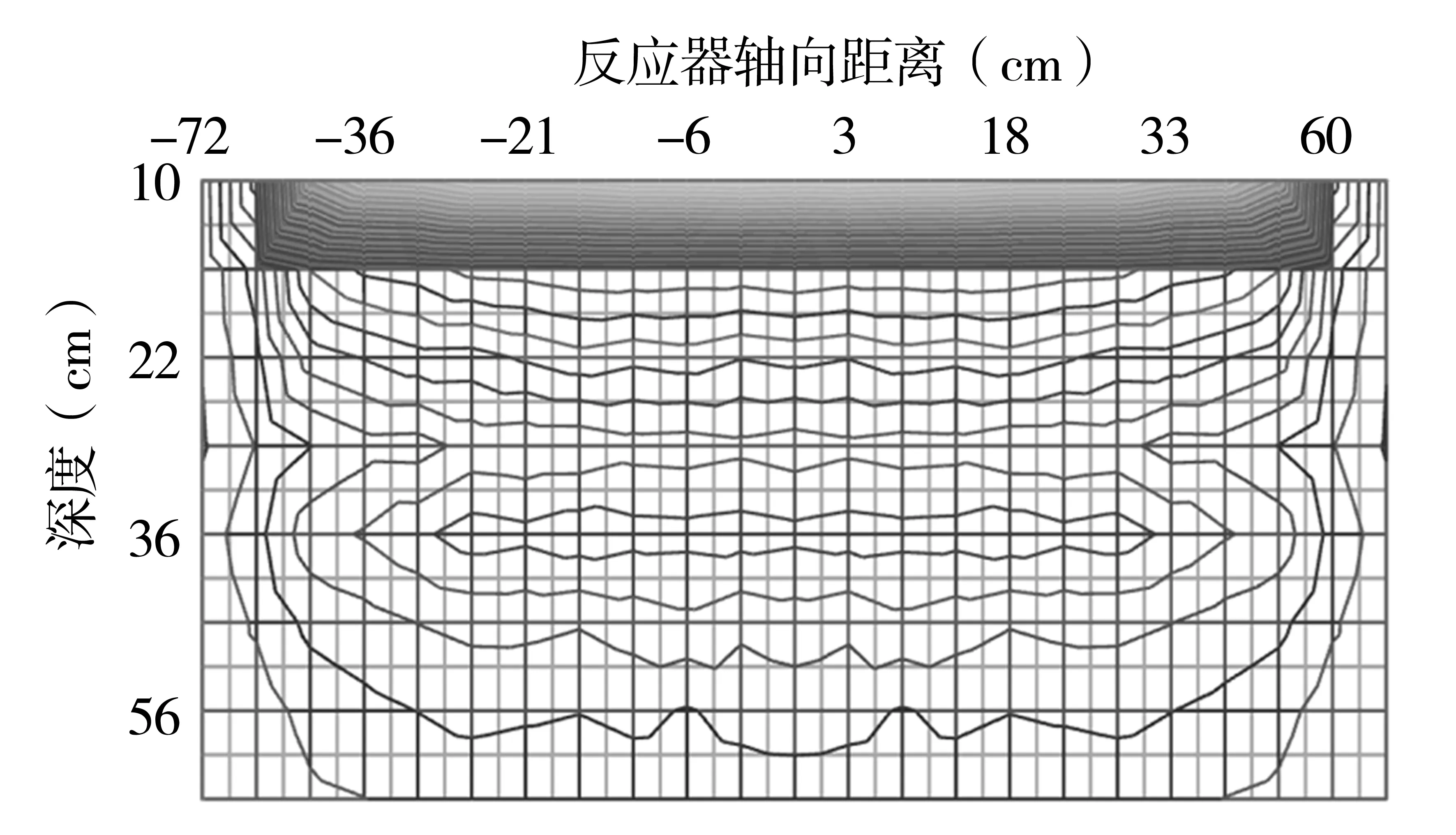
圖4 MCNP計算所得反應器剖面劑量場

圖5 反應器剖面劑量場(實測)[1]
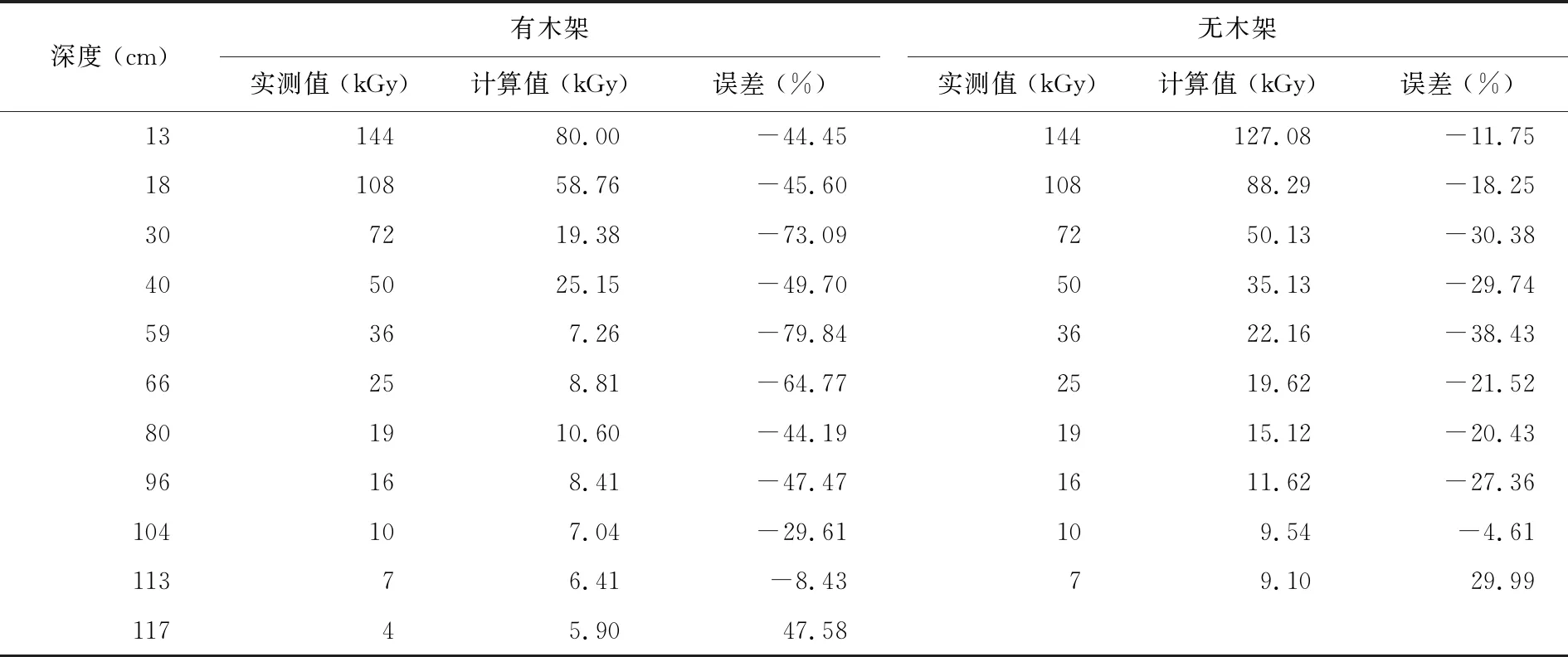
表1 MCNP模擬結果與試驗值的對比
由表1可見,MCNP計算值與試驗擬合值間最小絕對值偏差為8.43%;最大絕對值偏差為79.84%,出現在反應器木架深度區域;完全去掉木架后得到的計算值(理論值),其與試驗值的最大絕對值偏差也達到38.43%,這與文獻[6,7]EGS4程序的結果偏差34.7%較為接近。
表2給出了相同幾何條件下,MCNP與EGS4模擬計算結果,兩者最大絕對值偏差為25.7%,可能是EGS4本身考慮的物理過程更全面、且具體計算時EGS4選取的探測柵元體積更大所致。
程序驗算結果與文獻[2]實驗結果的較大誤差(實驗結果未見理論分析中出現的“山坳效應”)可能是實驗中木架位置與理論計算有一定偏離,且實驗值經Matlab擬合修正后引入的。

表2 MCNP模擬結果與EGS4模擬結果對比(無木架)
3 結語
MCNP與EGS4各有側重。相比MCNP,EGS4涉及的物理過程更全面,在電子模擬過程中,EGS4比MCNP更為適用,這也是前人通常采用EGS4程序模擬電子束氨法脫硫反應器內部劑量率的原因,但EGS4采用高級計算機編程語言進行建模輸入,不如MCNP簡單,從這個角度來說,MCNP可操作性要好于EGS4。結果表明:
(1) 用MCNP“小孔成像”的方法模擬電子束氨法脫硫反應器內部劑量場總體是可行的。
(2) 為減小測量誤差,試驗可改用更細的輕金屬絲線綁扎固定劑量片的方法,以消除固定裝置對反應器內部劑量場的影響。

