自適應聯邦卡爾曼濾波的時間配準方法

趙明亮，汪立新，秦偉偉

(火箭軍工程大學 導彈工程學院，陜西 西安 710025)

0 引言

組合導航信息融合系統中存在系統誤差與隨機誤差，傳感器時間配準問題主要是為了消除系統誤差[1]。

由于傳感器的采樣頻率、測量誤差、采樣起始時間的不同等，在進行多傳感器信息融合處理前應把傳感器數據同步至相同時刻，這個過程稱為時間配準[2]。實際應用表明不進行時間配準或配準精度不高，都可能導致信息融合結果不理想[3]。目前常用的時間配準方法有泰勒展開修正法、最小二乘法、內插外推法、最大熵準則法和濾波方法等。

文獻[4]應用泰勒展開修正法來修正時間數據，但算法要求采樣間隔必須為等間隔，且算法存在近似計算，配準精度不高；文獻[5-7]采用最小二乘規則對多傳感器數據進行虛擬融合，但采樣點必須嚴格對應、起始采樣點必須相同且配準精度較低；文獻[8-9]采用曲線擬合最小二乘法進行時間配準，但當配準時刻在擬合曲線的端點處就存在發散情況，致使配準精度在端點處急劇下降，影響配準精度。文獻[10]提出的內插外推法要求系統運動狀態確定，且算法配準精度不高；文獻[11-12]運用最大熵準則與最小均方估計來對不同速率信號進行配準，但算法對量測信號的統計特性和不同量測間相關度有要求，且精度較低；文獻[3]采用EKF(extended Kalman filter)算法對目標進行時間配準，但是該算法的濾波過程是在假設目標運動模型已知，若運動模型失配，則算法的配準精度急劇下降；文獻[13]采用H∞濾波法，但其通常僅在某種特定機動條件下精度相對較高，而復雜機動形式下不總是最優的。

本文針對現有時間配準算法存在的配準精度低、只能在限定條件下使用等不足，提出了一種基于自適應聯邦卡爾曼濾波的分段重疊采樣周期時間配準算法，通過對量測信息進行分段處理，將各個傳感器輸出的量測信息統一到同一時刻且不降低其精度，有效抑制了時間誤差影響。應用于SINS/GPS組合導航系統，實驗表明算法能有效提高濾波精度、數據平穩性，具有工程意義。

1 組合導航時間誤差分析

已知慣導系統比力方程如下[14]：

(1)

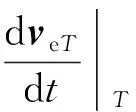
不考慮誤差，由式(1)可得速度理想值為

(2)

實際系統中考慮誤差，實際速度為

(3)

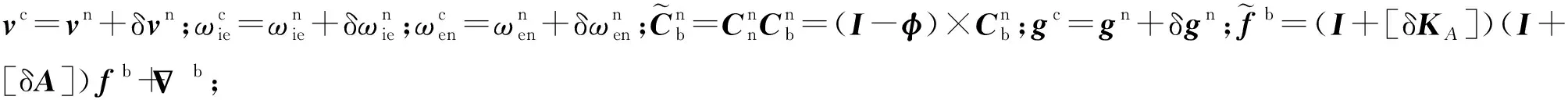
[δKA]=diag(δKAx,δKAy,δKAz);

式中:φE,φN,φU為姿態誤差角;δKAi和δAi分別為加表刻度系數誤差和安裝誤差角。

用式(3)減去式(2)，忽略δgn的影響，略去二階小量，得

(4)

又由四元數法推導得出姿態誤差方程為[14]

(5)

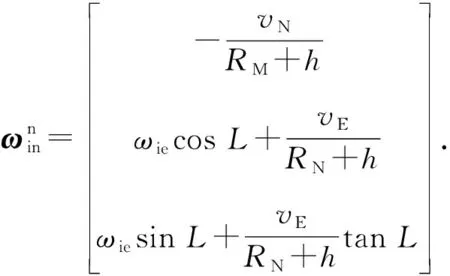
首先分析時間誤差對速度估計的影響，建立組合導航系統量測方程，則速度觀測量為

(6)

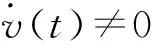
(7)

當系統作直線加速運動時，速度狀態變為

(8)

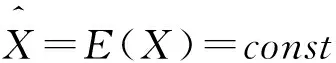
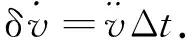
(9)

由式(8)知，直線加速運動時，時間誤差Δt影響速度估計量，但Δt一般為小量，此種情況可不計。

當系統作圓周運動時，速度狀態變為

(10)

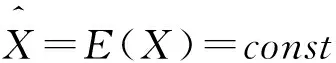
(11)

由式(10)知，系統作圓周運動時，時間誤差與系統方位角有信息一致性，在進行數據濾波時，會把時間誤差的來源歸于方位角，進而直接造成方位角的估計錯誤，給速度估計帶來較大誤差。由上述分析可知，載體的牽連加速度是時間誤差對速度估計的主要來源。

其次，分析時間誤差在對位置估計的影響。已知位置誤差如下：

(12)

建立組合導航系統量測方程，則位置量測為

(13)

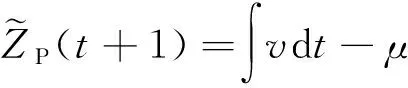
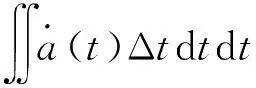
綜上所述，時間誤差會對速度估計與位置估計產生影響。為提高組合導航系統精度,對時間誤差必須加以消除。

2 分段重疊時間配準算法

在組合導航系統中，由于傳感器的測量數據不同步(初始采樣時刻不同、采樣頻率不同、傳輸延遲等)從而導致時間誤差。圖1所示在有4個傳感器A，B，C，D的組合導航系統中。A與B采樣間隔不同且起始時刻不同；A和C為異類傳感器采樣間隔不同；A和D采樣率雖然相同但由于有傳輸延遲等因素的影響造成采樣不同步。

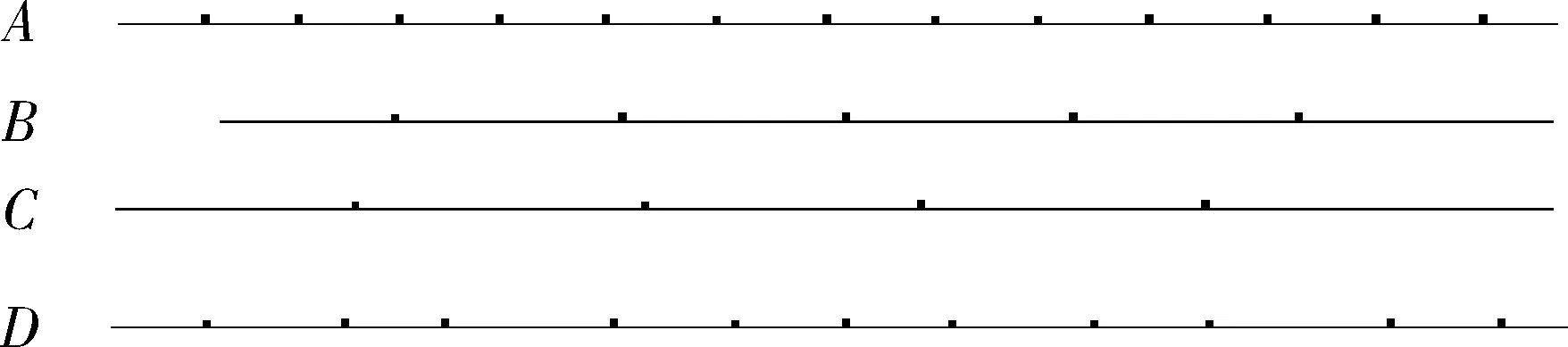
圖1 多個傳感器時間誤差圖Fig.1 Time error schematic diagram of multi-sensor system

分段重疊配準算法步驟如下：

第1步：進行分段處理，確定分段間隔ΔT。分段間隔的選取必須保證在間隔內每個傳感器都應有測量值，故分段間隔ΔT須大于等于最大傳感器采樣間隔，即ΔT≥Tmax。

第2步：進行重疊處理，確定重疊區間T′。重疊區間的選取既要考慮高的采樣率又要考慮計算機實時計算的時效性，故重疊區間T′考慮選取各個傳感器采樣周期的均值且應排除最值情況。故T′為

(14)

式中：n為傳感器的數量；Ti為各傳感器采樣周期；Tmax為各傳感器中采樣周期的最大值；Tmin為各傳感器中采樣周期的最小值。

第3步：確定組合系統處理區間。配準算法的目的是為了將多傳感器的量測信息分別整合到處理區間。定義系統接收到量測信息的時刻為配準起始時刻T0，則配準區間為：[T0+nΔT,T0+nΔT+T′]。

第4步：進行量測投影，確定傳感器在處理區間的量測值。使用最小二乘法進行估計[15]。

(15)

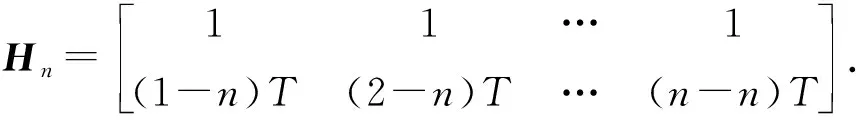
應用最小二乘法可解得其最小二乘解及其相應方差陣估計值如下：

(16)

(17)

第5步：進行數據濾波，得到各傳感器濾波量測值。

通過步驟4便可得到各傳感器處于同一時刻且間隔區間為T′量測估計值，作為各傳感器量測值。設計聯邦卡爾曼濾波器對組合導航系統進行估計，經典聯邦卡爾曼濾波器在實際應用時，由于環境等不確定因素的影響，各子傳感器和局部濾波器的濾波性能可能會發生變化[16]。故本文設計按即時性能調整的信息分配因子的自適應聯邦卡爾曼濾波器。

由各個子傳感器的系統方程，得到系統的狀態空間方程，離散化后可得狀態空間模型如下：

(18)

自適應聯邦卡爾曼濾波設計如下：

(1) 信息分配

(19)

式中：βi為信息分配因子，且滿足信息守恒定律：

(20)

(2) 時間更新

(21)

(22)

(3) 量測更新

(23)

(24)

(25)

(4) 信息融合

(26)

(27)

(5) 基于濾波協方差陣特征值分解，估計誤差協方差陣Pi按其特征值分解為

Pi=LΛiLT,

(28)

式中：Λi=diag{λi1,λi2,…,λin}，λi1,λi2,…,λin為Pi的特征值。

由Pi的定義可知以λi1,λi2,…,λin與估計狀態的估計誤差方差相對應。故使

(29)

式中：trΛi表示矩陣的跡，在數學上定義為Λi的特征值的和。

3 實驗驗證

設計實際的組合導航系統為實驗對象進行推車實驗，組合導航系統采用中航618所生產的某型激光捷聯慣性/衛星組合導航系統，如圖2所示。

圖2 實驗設備圖Fig.2 Experimental equipment diagram

組合導航系統模式選取為“緊組合”，采樣輸出周期為10 s，實驗總共進行1 970 s。由于試驗在地面進行，且行進距離及速度有限，故忽略天向速度誤差及高度誤差。

實驗開始前先進行10 min慣組加溫和8 min左右的羅經對準(受實際環境影響)。推車初始位置為東經109.126 2°，北緯34.312 6°，高度463.3 m；初始速度為0 m/s，初始航向角與北向夾角45°；激光陀螺初始位置誤差5 m，初始速度誤差為0.1 m/s，初始姿態誤差為10′；GPS接收機的偽距白噪聲為5 m，偽距率白噪聲為0.01 m/s。SINS解算周期為0.02 s，GPS采樣率為1 pps，采樣周期為1 s。代入配準算法中，可得ΔT=1 s，T′=0.51 s。

實驗行進軌跡如圖3所示。速度信息與姿態角信息如圖4,5所示。

系統的狀態方程表示為

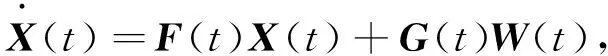
(30)

式中：

X(t)=(φE,φN,φU,δvE,δvN,δvU,δL,δλ,δh,

(31)

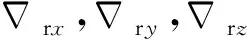
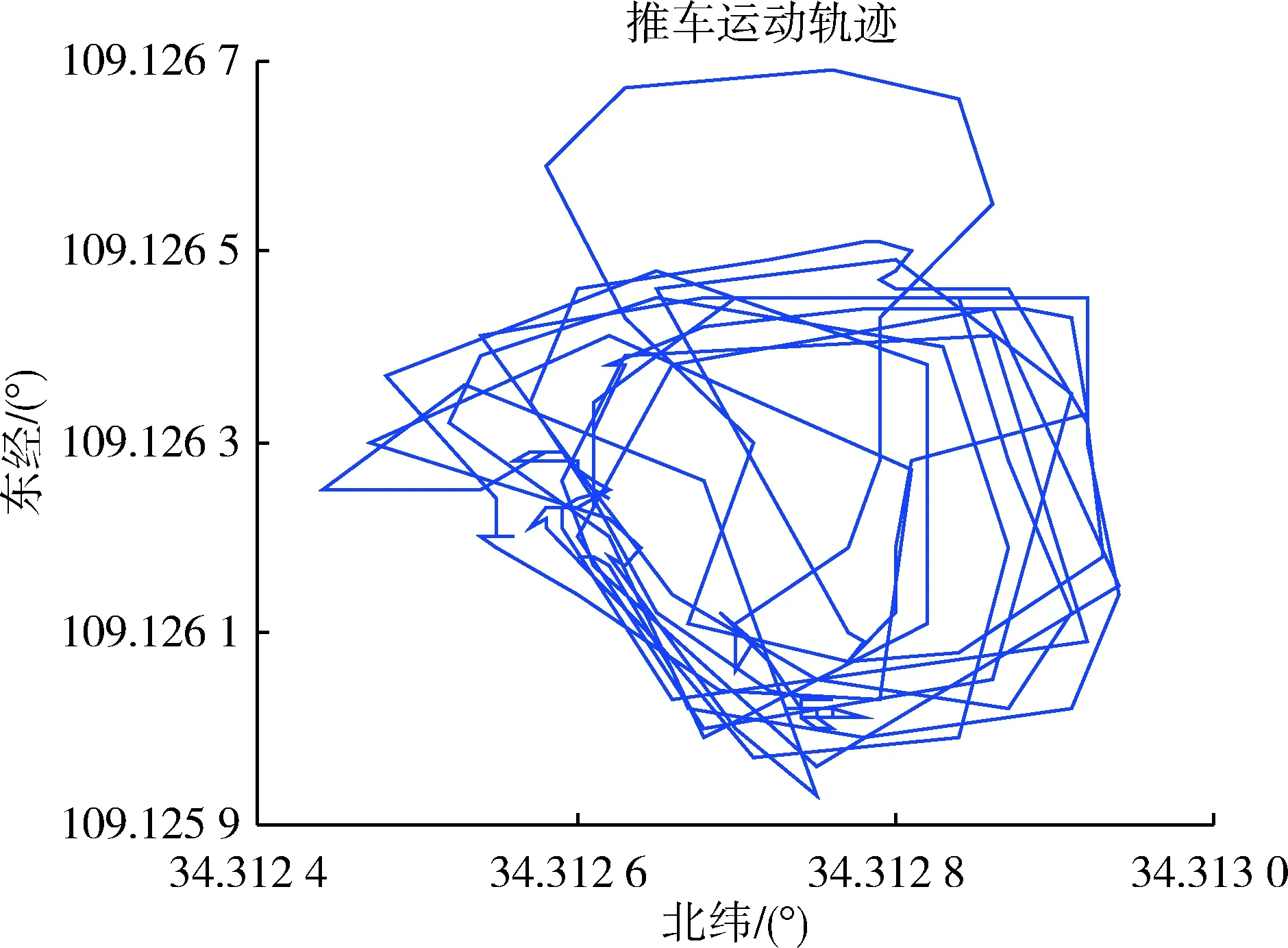
圖3 運動軌跡圖Fig.3 Path of particle

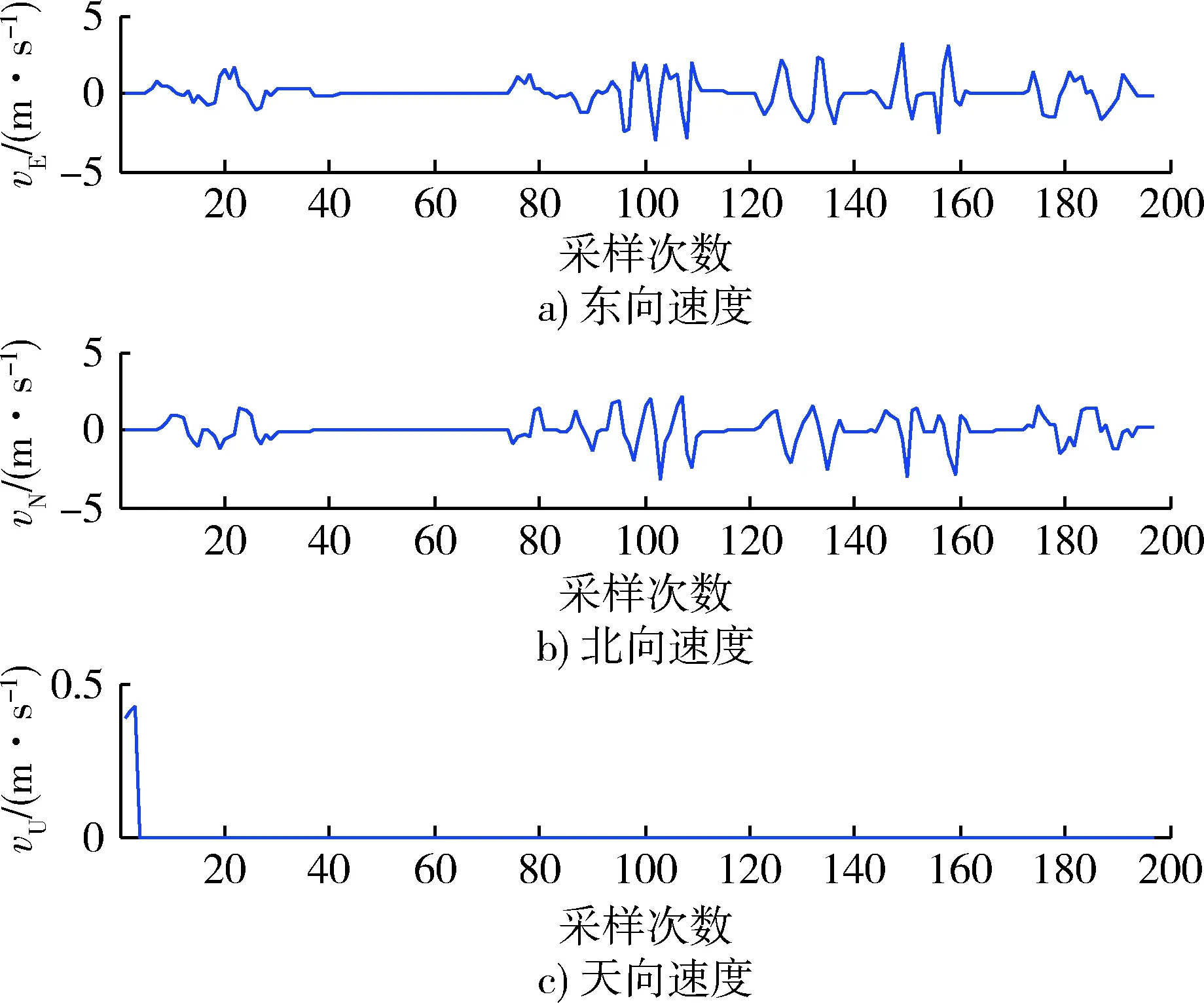
圖4 速度信息Fig.4 Speed information

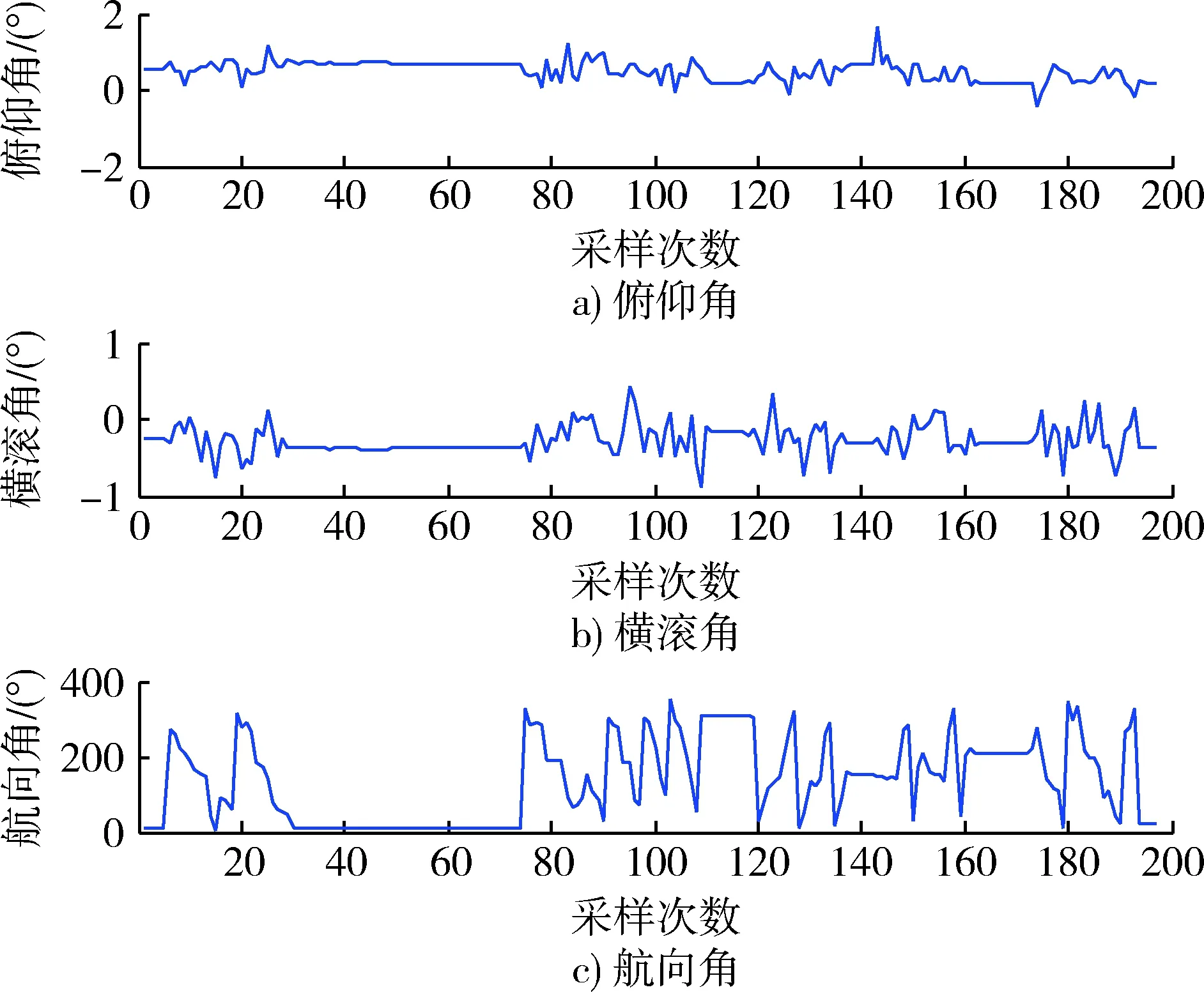
圖5 姿態角信息Fig.5 Attitude angel information

狀態轉移陣可表示為如下形式：

(32)

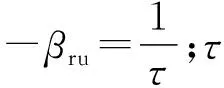
噪聲驅動陣G(t)可表示為如下形式：

(33)

噪聲陣W(t)可表示為

W(t)=(ωgx,ωgy,ωgz,ωax,ωay,ωaz,ωtu,ωtru)，

(34)

式中：ωgx，ωgy，ωgz為陀螺量測白噪聲；ωax，ωay，ωaz為加表量測白噪聲；ωtu和ωtru分別為鐘差白噪聲和鐘漂白噪聲。

偽距差量測方程如下：

Zp(t)=Hp(t)X(t)+Vp(t),

(35)

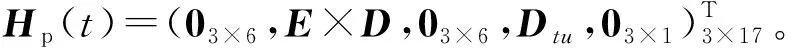
偽距率差量測方程如下：

Zv(t)=Hv(t)X(t)+Vv(t)，

(36)

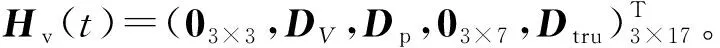
應用配準算法前后組合導航系統的位置誤差曲線與速度誤差曲線如圖6，7所示，各誤差項RMSE(root mean square error)如表1所示。由圖示誤差曲線可知，未進行配準時，估計誤差隨時間都有較大且無確定規律波動，由第1節時間誤差分析可知，這種不規律的波動與時間誤差的不規律性是一致的；而在應用配準算法后，緯度誤差RMSE減小53.29%，經度誤差RMSE減小55.54%，東向速度誤差RMSE減小47.79%，北向速度誤差RMSE減小27.71%，有效抑制了時間誤差，估計誤差顯著減小。

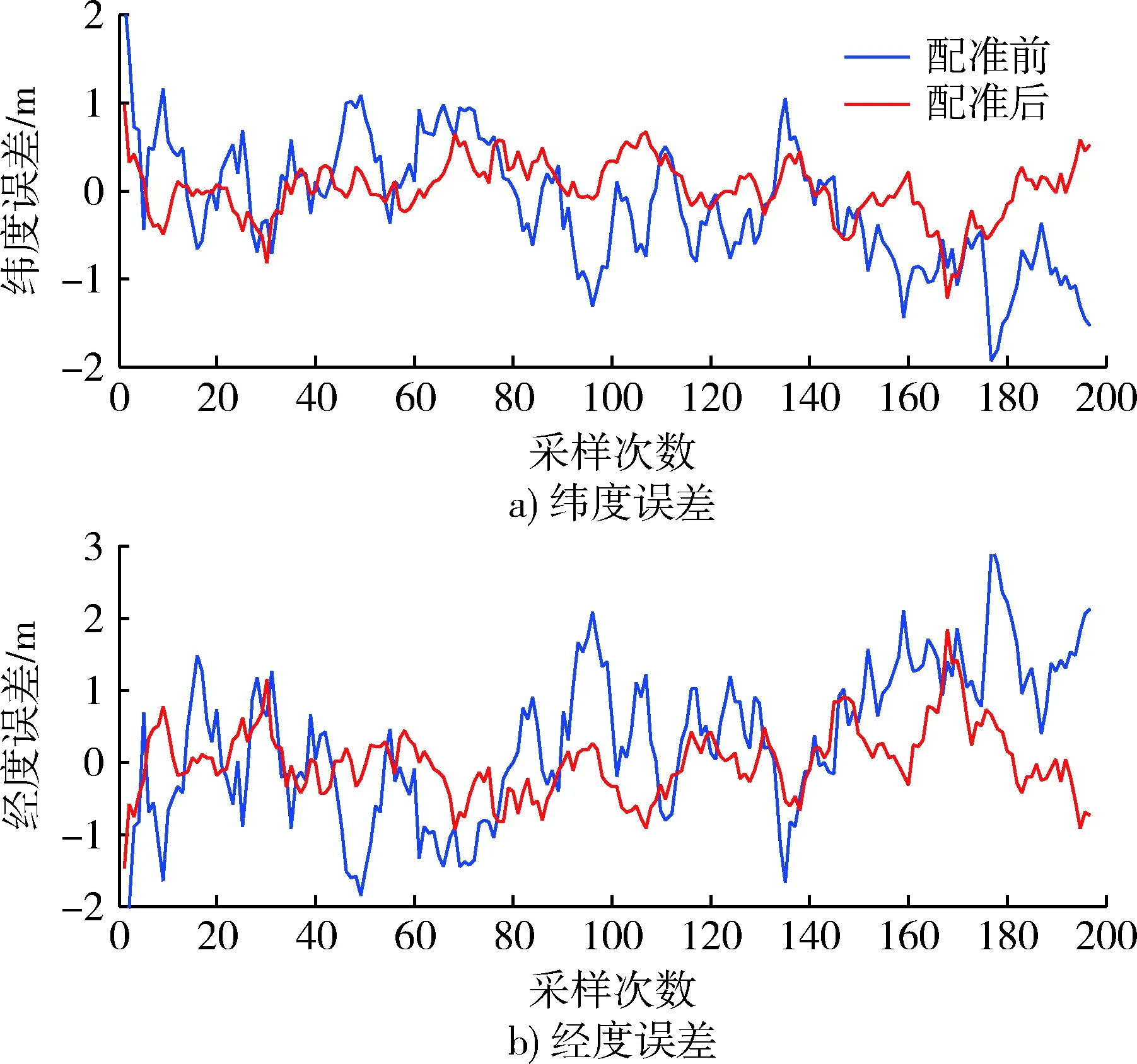
圖6 配準前后位置誤差曲線圖Fig.6 Position error curves before and after time registration

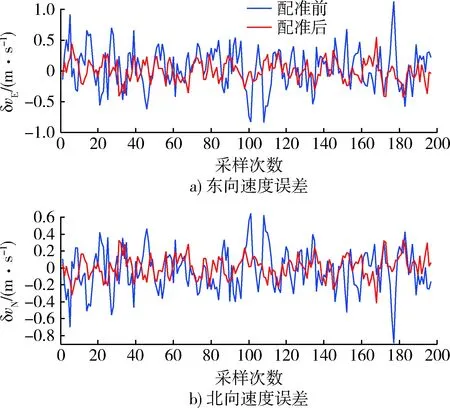
圖7 配準前后速度誤差曲線圖Fig.7 Velocity error curves before and after time registration

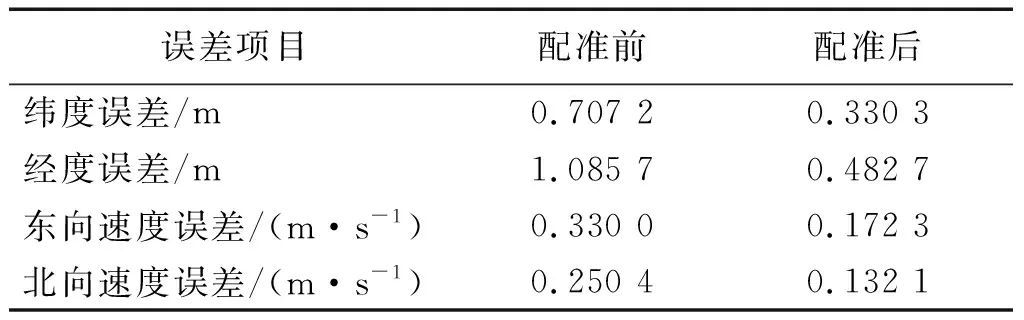
誤差項目配準前配準后緯度誤差/m0.707 20.330 3經度誤差/m1.085 70.482 7東向速度誤差/(m·s-1)0.330 00.172 3北向速度誤差/(m·s-1)0.250 40.132 1

4 結束語

本文提出一種基于自適應聯邦卡爾曼濾波的重疊分段時間配準算法。通過對傳感器量測信息進行重疊分區處理，將不同量測量統一至同一時刻處理。組合導航試驗表明，算法有效提高了采樣率與配準精度，抑制了不規則的時間誤差，顯著減小了系統估計誤差，提升了系統平穩性。且算法簡單易實現，有良好的應用前景。