MUSIC分級(jí)搜索策略研究

靳浩,王坤,張恒,沈義龍

(中國洛陽電子裝備試驗(yàn)中心，河南 洛陽 471003)

0 引言

波達(dá)方向估計(jì)在雷達(dá)、通信、聲吶等方面中有著重要的意義。傳統(tǒng)的測(cè)向方法由于受瑞利限的制約，其角度分辨率不能達(dá)到很高。而基于陣列信號(hào)處理的MUSIC(multiple signal classification)[1]算法可以實(shí)現(xiàn)角度的超分辨率估計(jì)。由于陣列方向矩陣與陣列輸出向量的協(xié)方差矩陣的信號(hào)子空間張成的空間相同(或與噪聲子空間正交)，MUSIC算法據(jù)此而構(gòu)建空間譜，根據(jù)其譜峰位置來確定波達(dá)方向。MUSIC算法具有測(cè)向精度高等優(yōu)點(diǎn)，但是由于其為搜索類算法，需要在立體空間內(nèi)進(jìn)行搜索，而為了保證測(cè)角精度，搜索間隔必須足夠小，因而搜索次數(shù)多，計(jì)算速度慢[2]。為了實(shí)現(xiàn)快速測(cè)向，有了很多的MUSIC改進(jìn)算法，如文獻(xiàn)[2-11]等提到的方法，文獻(xiàn)[12-14]還針對(duì)其中一些算法進(jìn)行了性能的比較。但這些方法都有一定的局限性，如對(duì)陣元排列形式有要求或者在陣元數(shù)較多時(shí)，其速度提升并不是很明顯等。一般為達(dá)到快速測(cè)向的目的，可以對(duì)搜索類算法采用分級(jí)搜索策略，即先進(jìn)行大間隔的粗搜索，而后再以粗搜索的結(jié)果作為初值，在初值附近進(jìn)行小間隔精搜索，以達(dá)到快速測(cè)向的目的。文獻(xiàn)[15-19]等提到了分級(jí)搜索算法可以大幅降低運(yùn)算耗時(shí)，但僅僅進(jìn)行兩級(jí)搜索且只是人為地設(shè)定搜索間隔等簡單的分級(jí)，并沒有針對(duì)最優(yōu)分級(jí)和搜索間隔進(jìn)行討論。本文針對(duì)MUSIC算法，進(jìn)行分級(jí)搜索處理，從理論上分析了各級(jí)分級(jí)算法耗時(shí)最少的分級(jí)策略，得到各級(jí)分級(jí)搜索能達(dá)到的最佳效果。并將各級(jí)搜索計(jì)算次數(shù)與直接搜索相比，分析其相對(duì)于直接搜索的運(yùn)算速度提升效果，得出最佳的分級(jí)搜索策略。最后利用Matlab平臺(tái)進(jìn)行了仿真實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果驗(yàn)證了理論的正確性。

1 MUSIC分級(jí)搜索策略

在每次估計(jì)來波方向時(shí)，接收數(shù)據(jù)的協(xié)方差矩陣和其特征值分解都只需要計(jì)算1次，但每個(gè)角度的空間譜計(jì)算則需要先計(jì)算導(dǎo)向矢量，而后計(jì)算空間譜，且這些運(yùn)算一般都是針對(duì)復(fù)數(shù)進(jìn)行的。這就導(dǎo)致在角度搜索上耗時(shí)過多，如果能夠降低角度搜索的次數(shù)，則對(duì)于運(yùn)算速度提升有很大的幫助。分級(jí)搜索可以很大程度上減少搜索計(jì)算次數(shù)，從而達(dá)到提升運(yùn)算速度的目的。下面針對(duì)多級(jí)分級(jí)搜索進(jìn)行分析。

1.1 直接搜索

以單目標(biāo)入射為例。首先是直接搜索，假設(shè)待搜索角度范圍為[-N,N]，要求的測(cè)角精度為Dg，那么在直接搜索情況下，需要進(jìn)行搜索計(jì)算的空間譜次數(shù)(1個(gè)方位角和1個(gè)俯仰角需要1次)為

(1)

1.2 2級(jí)搜索

分2級(jí)進(jìn)行譜峰搜索，第1級(jí)的搜索范圍為[-N,N]，間隔為Dg1，則第1級(jí)搜索計(jì)算的空間譜次數(shù)為

(2)

第2級(jí)的搜索以第1級(jí)搜索得到的角度為中心，角度搜索范圍為[-Dg1/2,Dg1/2]，間隔為Dg，則第2級(jí)搜索計(jì)算的空間譜次數(shù)為

(3)

總的搜索計(jì)算的空間譜次數(shù)為

(4)

式中：N與Dg在特定情況下可以視為已知量，則式(4)轉(zhuǎn)換為求在正數(shù)范圍內(nèi)能使f2取得最小值的解。

對(duì)式(4)求導(dǎo)，可得

(5)

令式(5)等于0，則有

(6)

即

(7)

由此可得Dg1的正數(shù)解為

(8)

此時(shí)總的搜索次數(shù)為

(9)

則2級(jí)搜索的搜索次數(shù)與直接搜索的搜索次數(shù)的比值為

(10)

1.3 3級(jí)搜索

分3級(jí)進(jìn)行譜峰搜索，第1級(jí)的搜索范圍為[-N,N]，間隔為Dg1，則第1級(jí)搜索計(jì)算的空間譜次數(shù)為

(11)

第2級(jí)的搜索以第1級(jí)搜索得到的角度為中心，角度搜索范圍為[-Dg1/2,Dg1/2]，間隔為Dg2，則第2級(jí)搜索計(jì)算的空間譜次數(shù)為

(12)

第3級(jí)的搜索以第2級(jí)搜索得到的角度為中心，角度搜索范圍為[-Dg2/2,Dg2/2]，間隔Dg，則第3級(jí)搜索計(jì)算的空間譜次數(shù)為

(13)

總的搜索計(jì)算的空間譜次數(shù)為

(14)

式中：

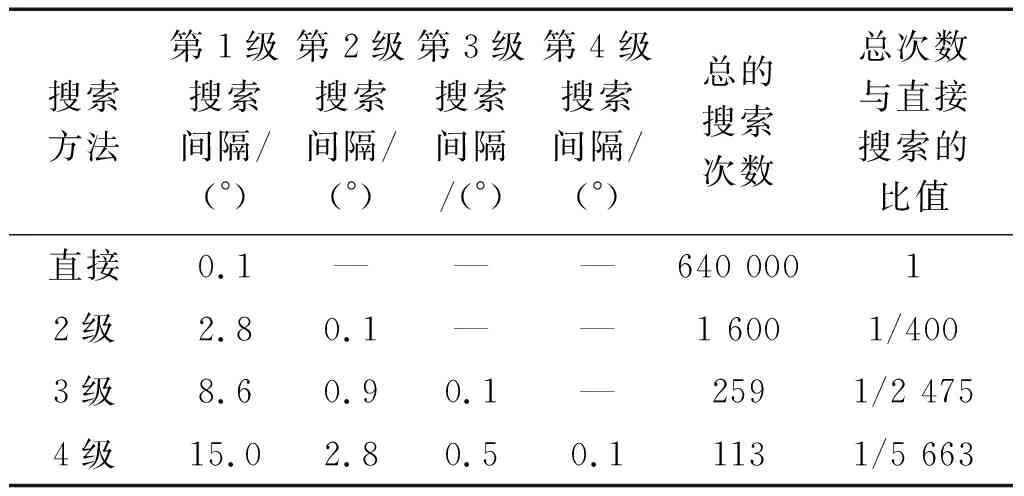
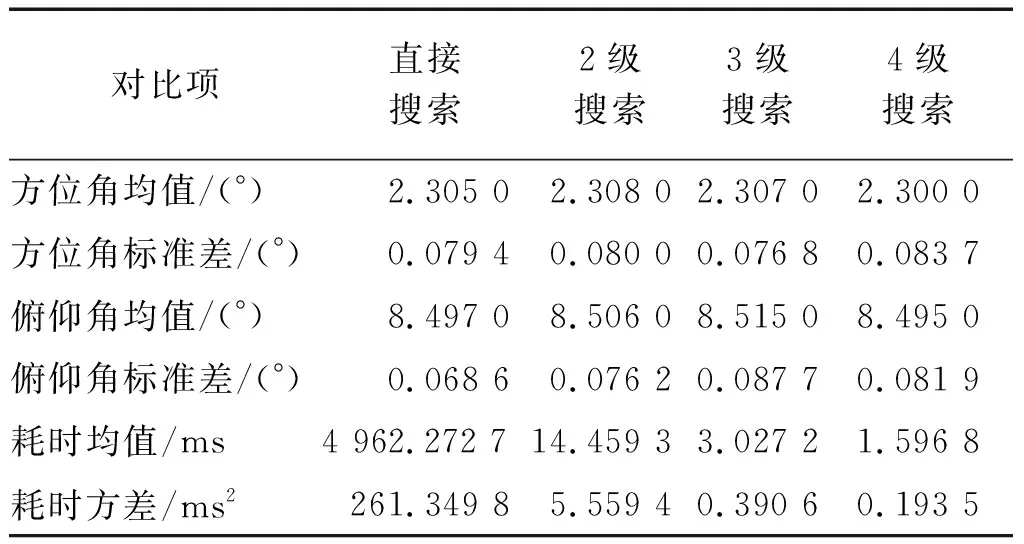
0

(15)

想要f3最小，即為求解

(16)

在式(15)情況下的極小值。對(duì)式(16)求偏導(dǎo)數(shù)，由二元方程求極值法則可知，在Dg1和Dg2滿足式(17)的情況下，f(Dg1,Dg2)可以取得極小值。

(17)

由式(17)可以解得

(18)

可知，在2N>Dg時(shí)，有Dg1>Dg和Dg2>Dg，且在N>Dg時(shí)，始終有Dg1>Dg2，滿足式(15)要求。此時(shí)，f(Dg1,Dg2)取最小值：

(19)

由此可得3級(jí)搜索的總搜索次數(shù)與直接搜索的搜索次數(shù)的比值為

(20)

1.4 M級(jí)搜索

對(duì)于M級(jí)搜索，總的搜索次數(shù)為

(21)

易知在

(22)

fM可以取得最小值。由此可以計(jì)算出各級(jí)搜索的最佳搜索間隔。

2 理論結(jié)果分析

從式(10)和式(20)可以看出，在MUSIC算法中，要求的精度Dg越高，搜索區(qū)間[-N,N]越大，多級(jí)搜索提升的運(yùn)算速度越多。例如，在[-40,40]范圍內(nèi)搜索(一般情況下，實(shí)際作戰(zhàn)環(huán)境中導(dǎo)引頭的搜索范圍)，要求精度為0.1，表1給出了理論計(jì)算的最優(yōu)情況下,直接搜索、2級(jí)搜索、3級(jí)搜索和4級(jí)搜索各自的每級(jí)搜索間隔和總的搜索次數(shù)，同時(shí)還給出了各級(jí)搜索的搜索總次數(shù)與直接搜索的搜索總次數(shù)的比值。

表1 多級(jí)搜索理論結(jié)果對(duì)比Table 1 Comparison of theoretical results of multi-level search

由表1可知，2級(jí)搜索相對(duì)于直接搜索，搜索次數(shù)明顯減少；3級(jí)搜索相對(duì)于2級(jí)搜索，搜索次數(shù)也減少了許多；4級(jí)搜索相對(duì)于3級(jí)搜索，搜索次數(shù)也有一定的減少。

由此可見，多級(jí)搜索可以在很大程度上降低運(yùn)算耗時(shí)，提高運(yùn)算速度。但是其相對(duì)于上一級(jí)的搜索(如3級(jí)搜索相對(duì)于2級(jí)搜索)提升效果明顯小于上一級(jí)搜索相對(duì)于其上一級(jí)搜索(如2級(jí)搜索相對(duì)于直接搜索)的提升效果。特別是4級(jí)搜索以后，其速度提升有限，可以不必考慮。

實(shí)際上，在具體運(yùn)算中，2級(jí)以上分級(jí)搜索計(jì)算次數(shù)要小于上述計(jì)算的次數(shù)。這是因?yàn)閺睦碚撋嫌?jì)算次數(shù)時(shí)，包含了小數(shù)部分，而實(shí)際中則會(huì)對(duì)小數(shù)向下取整。如在3級(jí)計(jì)算中，第1級(jí)計(jì)算次數(shù)為(80/8.6)2，約為9.32，大約86.5，而實(shí)際中只需要9×9=81次。

3 仿真實(shí)驗(yàn)

為了更好的驗(yàn)證理論分析的正確性，利用Matlab進(jìn)行了仿真實(shí)驗(yàn)。實(shí)驗(yàn)中采用陣列為均勻間隔L陣，9個(gè)陣元，除去原點(diǎn)，x和y方向各4個(gè)陣元，陣元間隔為半波長。入射信號(hào)頻率為4.5 GHz，方位角為2.3°，俯仰角為8.5°，信噪比為14 dB，使用100個(gè)采樣點(diǎn)數(shù)據(jù)計(jì)算接收數(shù)據(jù)的協(xié)方差矩陣(簡稱R陣)，進(jìn)行100次蒙特卡羅模擬實(shí)驗(yàn)。

圖1給出了100次實(shí)驗(yàn)的方位角和俯仰角測(cè)試結(jié)果。圖2給出了100次實(shí)驗(yàn)的耗時(shí)結(jié)果。表2則給出了直接搜索、2級(jí)搜索、3級(jí)搜索和4級(jí)搜索4種方法耗時(shí)(此處的耗時(shí)為搜索計(jì)算空間譜耗時(shí)，鑒于R的計(jì)算是必不可少的，且譜峰搜索是實(shí)數(shù)運(yùn)算，相對(duì)于搜索計(jì)算空間譜的復(fù)數(shù)運(yùn)算，耗時(shí)較少，沒有統(tǒng)計(jì)計(jì)算R陣與譜峰搜索的耗時(shí))與精度對(duì)比。

對(duì)比項(xiàng)直接搜索2級(jí)搜索3級(jí)搜索4級(jí)搜索方位角均值/(°)2.305 02.308 02.307 02.300 0方位角標(biāo)準(zhǔn)差/(°)0.079 40.080 00.076 80.083 7俯仰角均值/(°)8.497 08.506 08.515 08.495 0俯仰角標(biāo)準(zhǔn)差/(°)0.068 60.076 20.087 70.081 9耗時(shí)均值/ms4 962.272 714.459 33.027 21.596 8耗時(shí)方差/ms2261.349 85.559 40.390 60.193 5

從圖1中可以看出，無論是方位角還是俯仰角，4種搜索方法測(cè)角結(jié)果大致相同，實(shí)驗(yàn)中俯仰角和方位角估計(jì)值在真值附近上下波動(dòng)。從表2的均值中也可以看出，4種測(cè)角方法，方位角和俯仰角的估計(jì)均值與真值的誤差較小，且測(cè)角精度大致相同。而4種方法的測(cè)角方差也是很小。

從圖2中可以看出，4種測(cè)角方法中直接搜索耗時(shí)最多，平均耗時(shí)大約4 962.2 727 ms，2級(jí)搜索平均耗時(shí)14.459 3 ms，約為直接搜索的1/343；3級(jí)搜索平均耗時(shí)3.027 2 ms，約為直接搜索的1/1 639，約為2級(jí)搜索的1/4.7；4級(jí)搜索平均耗時(shí)1.596 8 ms，約為直接搜索的1/3 107，約為2級(jí)搜索的1/9.1，約為3級(jí)搜索的1/1.9。

結(jié)合前面的分析和實(shí)驗(yàn)結(jié)果可以看出，多級(jí)搜索可以大大地減少運(yùn)算耗時(shí)，提高越算速度。而隨著分級(jí)增多，提高效率明顯降低。4級(jí)搜索的耗時(shí)相對(duì)于3級(jí)搜索的耗時(shí)已經(jīng)減少不多，再加上計(jì)算R陣與譜峰搜索的耗時(shí)，4級(jí)搜索相對(duì)于3級(jí)搜索的速度提升可以忽略不計(jì)。且4級(jí)搜索第1級(jí)搜索間隔較大，在某些情況下，目標(biāo)的MUSIC空間譜譜峰寬度可能較小，甚至小于第1級(jí)搜索間隔，就會(huì)導(dǎo)致4級(jí)搜索算法失效，因而在實(shí)際應(yīng)用中對(duì)于單目標(biāo)測(cè)向使用3級(jí)分級(jí)搜索最優(yōu)。

對(duì)于多目標(biāo)入射信號(hào)，同樣可以利用前面的分析進(jìn)行處理，如有m個(gè)目標(biāo)，則第2級(jí)搜索的搜索次數(shù)需要乘以m，第3級(jí)搜索的搜索次數(shù)需要乘以m2，以此類推。對(duì)于M級(jí)搜索，同樣可以構(gòu)建一個(gè)M元函數(shù)，只需求解次M元函數(shù)在特定情況下的極小值即可。由此就可以獲得m個(gè)目標(biāo)的最優(yōu)分級(jí)搜索策略。

4 結(jié)束語

本文首先從理論上分析了MUSIC算法的分級(jí)搜索策略，根據(jù)搜索計(jì)算空間譜的次數(shù)來確定最優(yōu)的分級(jí)搜索策略，得出分級(jí)搜索可以大幅降低運(yùn)算耗時(shí)的結(jié)論，并利用Matlab進(jìn)行了仿真實(shí)驗(yàn)，驗(yàn)證了理論的正確性。下一步工作將會(huì)針對(duì)信噪比、采樣數(shù)、目標(biāo)雷達(dá)數(shù)等對(duì)分級(jí)搜索策略的影響進(jìn)行分析。