自由空戰中距轉彎機動對策生成問題研究

嵇慧明，余敏建，楊家一，張薇，游航航

(1.空軍工程大學a.研究生院；b.空管領航學院，陜西 西安 710051； 2.忻州師范學院 計算機系，山西 忻州 034000)

0 引言

廣義自由空戰是指在空中對抗中，空戰雙方在三維空間內充分發揮飛機的極限性能，合理使用各種機載武器，根據掌握的空中態勢，結合地面指揮所的引導對策，靈活自由地運用戰術對策，構成攻擊條件并進行攻擊[1]。根據空空導彈的射程，可將空戰階段分為近距空戰(10 km以內)、中距空戰(10～100 km)、遠距空戰(100 km以外)[2]。近距空戰[3]通常為視距內空戰，以機載航炮為主要武器，空戰機動決策以飛行員的經驗判斷為主，對地面指揮引導依賴度較小；遠距空戰主要依賴機載雷達與空空導彈，機動對策以占位布勢為主要目的，最終還要進入中距空戰對敵實施攻擊。因此，自由空戰中距轉彎機動對策生成，是未來一段時期內重點關注和重要的研究方向。

目前國內外在空戰機動對策的研究方面取得了豐碩的成果。主要的方法有：微分對策法[4]、影響圖法[5]、矩陣博弈法[6]、矩陣對策法以及基于“IF-THEN”規則、風險性決策[7]、遺傳算法[8]、戰術免疫機動系統[9]等的人工智能算法，這些方法主要為中近距的自由空戰實時對抗提供輔助決策，而對中距空戰轉彎機動對策生成問題研究較少。本文主要依據空空導彈攻擊區邊界函數以及空戰態勢優勢函數，建立自由空戰中距轉彎機動矢量模型，求解生成輔助引導對策，以有效解決中距轉彎機動對策生成問題。

1 中距轉彎機動對策生成影響因素分析

自由空戰中，飛行員會依據預先設定的戰法，結合空戰態勢和地面指揮引導策略，對戰機實施機動。影響戰機中距轉彎機動對策生成的因素主要有戰機與目標機的導彈最大攻擊區和戰機當前態勢2個方面。

1.1 導彈攻擊區

導彈攻擊區又稱殺傷包線，是指在一定攻擊條件下，由導彈性能決定的有可能命中目標的空間區域，在攻擊區內發射導彈才有可能命中目標[10]。文獻[11]將空空導彈最大攻擊區的邊界函數描述為

Dmmax=f(h,hm,v,vm,ny,q)，

式中：Dmmax為導彈最大攻擊區邊界；h為載機高度；hm為目標高度；v為載機速度；vm為目標速度；ny為目標機動過載；q為進入角。

為了簡化中距轉彎機動模型，可將導彈最大攻擊區邊界視為橢圓，并用極坐標方程：L=L(θ)進行求解。如圖1所示，θ表示與飛機航向的夾角，并定義右半球為正，左半球為負；L表示與飛機航向夾角成θ時導彈攻擊區邊界距離。

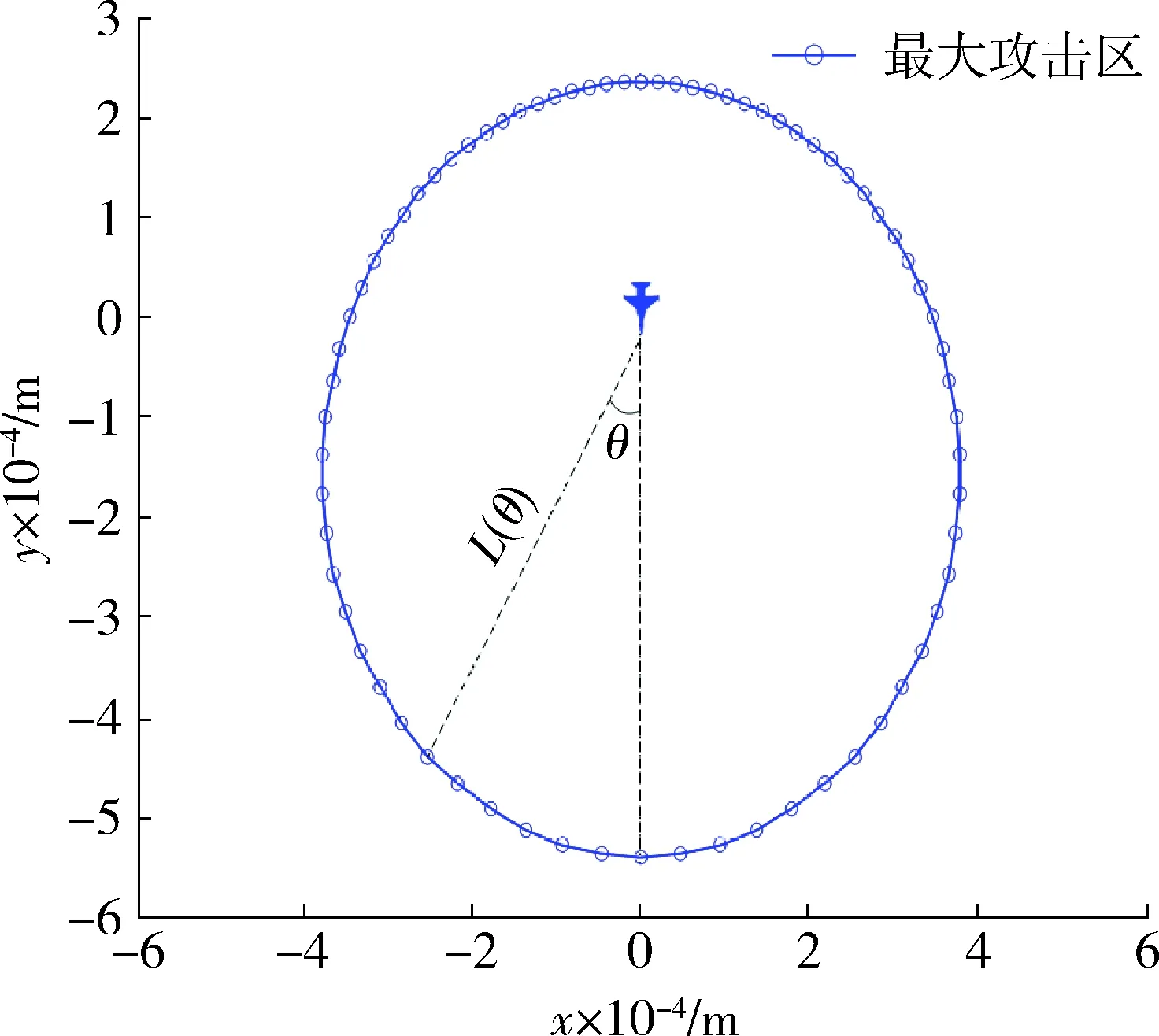
圖1 導彈最大攻擊區邊界Fig.1 Boundary of missile maximum attack zone

1.2 戰機優勢函數

空戰對策生成就是指揮戰機按照預定的高度、航向和速度等飛行諸元飛行，對敵構成有利空中態勢，占據有利戰術位置。數學描述上，根據當前的空戰態勢，構建相應的戰機優勢函數，選擇對應的戰機機動動作，使戰機達到最大空戰優勢。文獻[12]給出了角度、距離、速度、高度優勢函數并加權得到空戰優勢綜合函數。

1.2.1 戰機角度優勢函數

戰機的角度優勢主要體現在目標方位角φ和進入角q，φ與q的變化范圍為0～π，文獻[13]將φ與q分別劃分為如下3個區域：

式中：φrmax為雷達最大搜索方位角；φmmax為空空導彈最大離軸發射角；φmkmax為空空導彈不可逃逸區最大偏角。并由此建立戰機角度優勢函數：

(1)

1.2.2 戰機距離優勢函數

自由空戰戰機中距轉彎機動時，戰機通常不會進入目標機導彈最大攻擊區。因此，構建的距離優勢函數只與兩機間的相對距離、目標機導彈最大攻擊距離以及機載雷達最大搜索距離有關，計算公式為

式中：D為戰機與目標機之間的相對距離;Dr為雷達最大探測距離。

1.2.3 戰機速度優勢函數

通常情況下，戰機的速度越大，優勢越明顯。但在實際空戰中，速度越大，戰機轉彎半徑越大，攻擊占位時間變短，命中率也隨之下降。基于此，文獻[14]中引入了最佳空戰速度vbest，vbest與戰機和目標機間的相對距離有關：距離較大時，vbest大便于戰機快速接近目標機；距離較小時，vbest小便于戰機實施占位進行攻擊。利用vbest構造速度優勢函數如下：

(1) 當vbest>1.5vm時

(2) 當vbest≤1.5vm時

式中：vw為我方戰機速度;vm為目標機速度。

1.2.4 戰機綜合優勢函數

綜上可得，自由空戰中，戰機綜合優勢函數為

S=ωaSa+ωrSr+ωvSv，

(2)

式中：ωa,ωr,ωv分別為戰機角度優勢函數、距離優勢函數和速度優勢函數對應的權系數，且∑ωi=1,i=a,r,v。在不同空戰態勢下，戰機優勢函數的各個參數重要程度不同，其權系數計算公式[15]為

式中：ωi0為各參數的初始權系數值;ki為權系數的調節系數，∑ki=0,i=a,r,v。

2 中距轉彎機動矢量模型

自由空戰戰機中距轉彎機動建模，首先應對戰機的機動動作進行模擬仿真，將抽象的空間描述轉化為數學語言，并設立變量對戰機機動動作進行控制；其次，針對空戰過程中建立戰機坐標困難的特點，本文建立了矢量模型，通過矢量方程來表述兩機之間的相對關系，可以優化計算復雜度，提升戰機機動的有效性。

2.1 矢量模型簡介

在平面直角坐標系下，戰機與目標機間的態勢可用相對距離和相對方位角來衡量。根據直角坐標和當前航向，通過歐拉方程轉換，可以將兩機的矢量描述用復數表達式表示出來，再代入到矢量方程中，即可建立相應的矢量模型，從而解算出未知變量。

2.1.1 函數與符號定義

(1) 反正切函數

根據某點平面直角坐標(x,y)的所在象限，其反正切函數定義如下：

(2) 轉彎方向

(3) 進入方向

(4) 戰機至目標機方向

Kwm=at(xm-xw,ym-yw).

(5) 轉彎半徑

式中:γi為戰機的轉彎坡度。

(6) 兩機之間的距離

2.1.2 飛行過程矢量表示

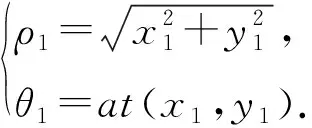
在復平面上，其復平面坐標為

A=y1+ix1.

經過時間t1后，到達位置點B(x2,y2)，則矢量AB在復平面上可表示為

AB=(y2-y1)+i(x2-x1).

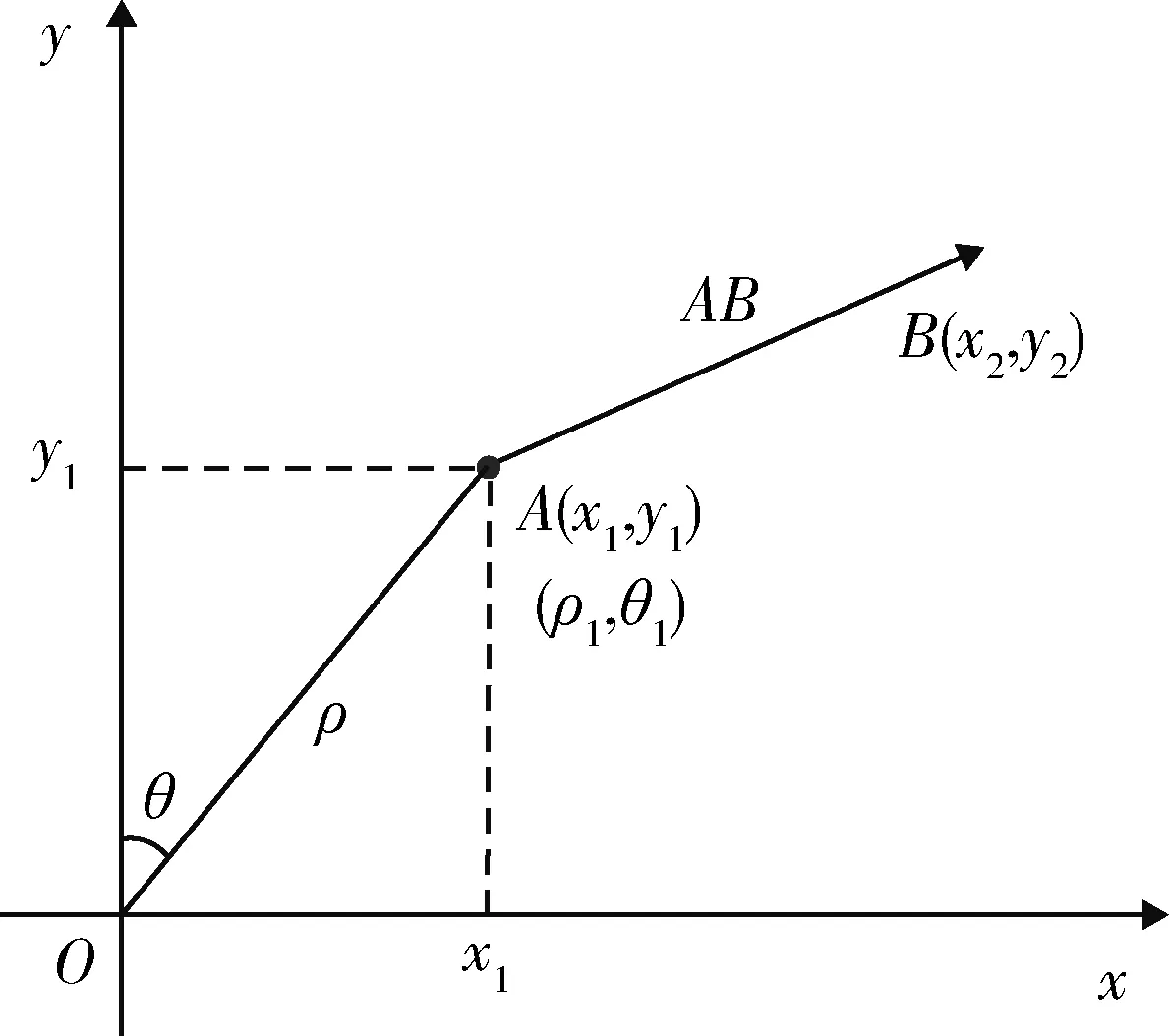
圖2 戰機飛行過程矢量表示Fig.2 Vector representation of fighter′s flight process

設A至B的距離為S,指向為K，則有

AB=S(cosK+isinK),

結合歐拉公式：

eiK=cosK+isinK,

所以

AB=SeiK.

2.2 戰機機動動作

文獻[16]得到了11種戰機機動改進后的基本操縱動作，并給出了每個動作的控制算法。本文中，戰機實施中距轉彎機動時，高度基本保持不變，主要涉及減速前飛、勻速前飛、加速前飛、左轉和右轉5種機動動作。平面示意圖如圖3所示。

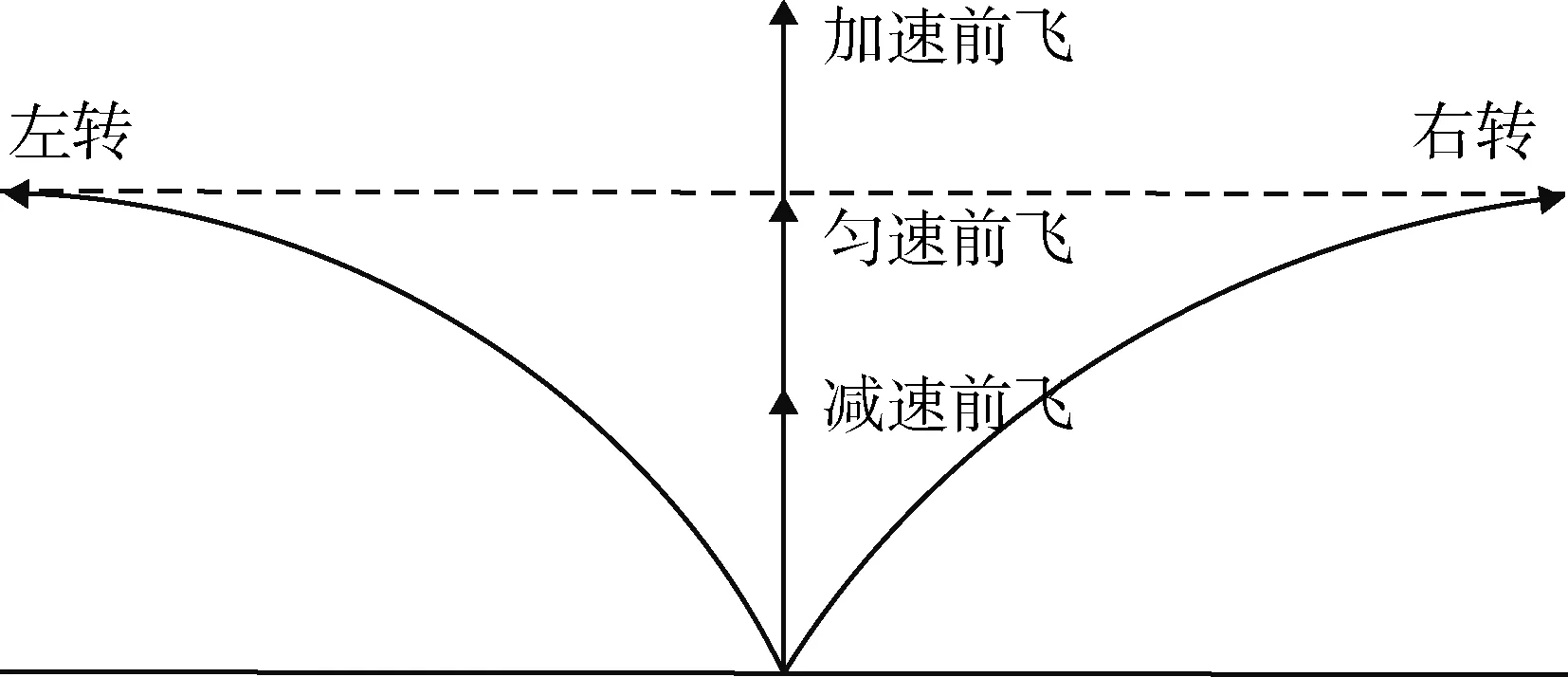
圖3 戰機主要機動動作Fig.3 Main maneuver of fighter planes

在數學描述上，本文選擇nx，ny，γ作為機動動作的控制變量。

式中：α,β,γ分別為戰機的航向角、航跡傾斜角、滾轉角；nx,ny分別為戰機的切向過載和法向過載。令

則上述5種機動動作對應的控制量范圍如表1所示。

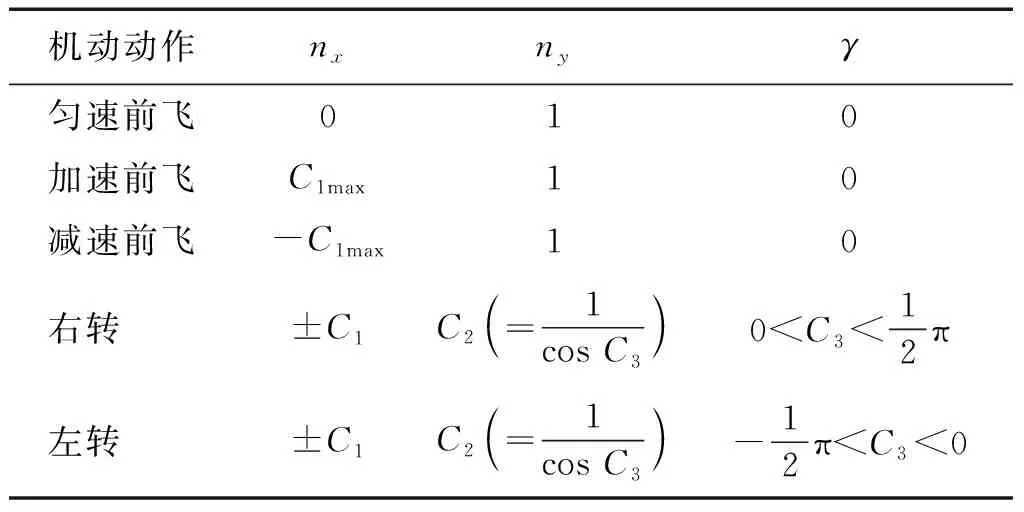
表1 戰機機動動作控制算法Table 1 Maneuver control algorithm for fighter plans

2.3 中距轉彎機動矢量模型的構建

初始時刻，戰機與目標機分別保持一定的速度、高度、航向飛行，通過戰機綜合優勢函數，計算戰機應飛航向、速度和高度，并以此調整戰機至應對目標機狀態，根據當前飛行諸元參數，結合兩機導彈攻擊區范圍和角度優勢函數，計算得出戰機中距轉彎時機和轉彎諸元(坡度、角度等)，從而生成中距轉彎機動引導對策。具體流程如圖4所示。

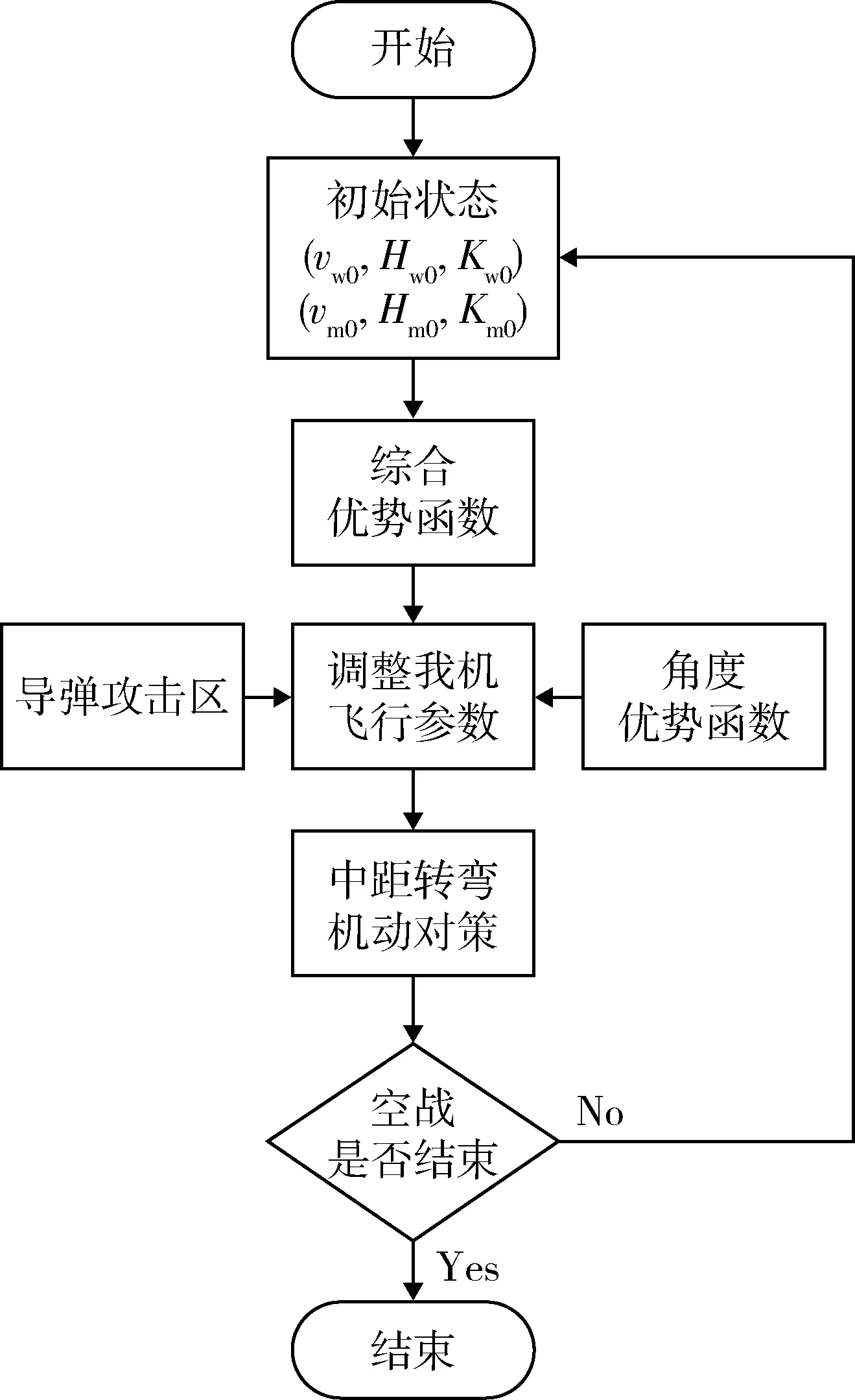
圖4 中距轉彎機動對策生成流程Fig.4 Generating process of maneuver countermeasures for mid-range turning

t0時刻，戰機與目標機分別位于W0(xw0,yw0)，M0(xm0,ym0)處，vw，vm，Hw，Hm，Kw和Km分別為兩機的速度、高度、航向。經過時間Δt后，戰機經過W1并實施中距轉彎機動到達W2處，目標機到達M1處，此時，戰機處于目標機導彈最大攻擊區外，而目標機處于我方戰機導彈最大攻擊區內，我方戰機占位構成優勢，在此處發射導彈或轉入近距作戰，可以有效提升我方戰機作戰效能。具體示意圖如圖5所示。

M1W2=M1M0+M0W0+W0W1+W1O1+

O1W2=-vm·ΔteiKm+S0eiKmw+

(3)

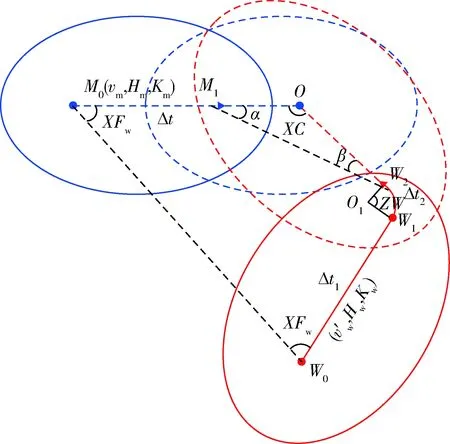
圖5 中距轉彎機動示意圖Fig.5 Schematic diagram of mid-range turning maneuver

(4)

建立時間方程：

(5)

式中：tzw代表轉彎時間。

戰機中距轉彎機動后，此時兩機的相對方位線與目標機和我方戰機航向夾角分別為α，β，由導彈最大攻擊區邊界函數可以得出最優距離：

式中：Lw(β)為與戰機航向夾角為β時導彈最大攻擊距離；Lm(α)為與目標機航向夾角為α時導彈最大攻擊距離。通過綜合優勢函數式(2)，可計算得出戰機接敵進角XC、接敵最優距離S1和α，β。

故有

M1W2=S1ei(Km+n1α)=vmΔtcos(Km+

n1α)+ivmΔtsin(Km+n1α).

(6)

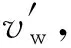
2.4 中距轉彎機動對策生成

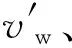
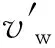
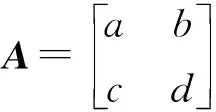
利用綜合優勢函數式(2)，結合導彈最大攻擊范圍，即可解算得出戰機轉彎改出航向。最后利用Matlab工具，仿真出戰機的飛行軌跡。

3 仿真分析

為了驗證該模型的有效性，現針對某空戰數據進行模擬仿真。目標機飛行軌跡嚴格按照該空戰戰法進行控制，我方戰機則通過中距轉彎機動模型計算得出空戰對策，用機動動作庫中的控制算法來模擬控制飛行。最后，通過與原戰法進行比較，并結合空戰綜合優勢函數，分析該模型的有效性。

初始時刻，目標機與我方戰機分別位于(10,10) km，(82.75,4)km處，兩機飛行參數分別為(8 000,800,90)，(8 000,1 100,270)，導彈最大攻擊區邊界函數是將真實數據理想化以后構建的橢圓方程，具有一定的可靠性。規定重力加速度g=10 m/s2，仿真步長為3 s，仿真結果如圖6所示。

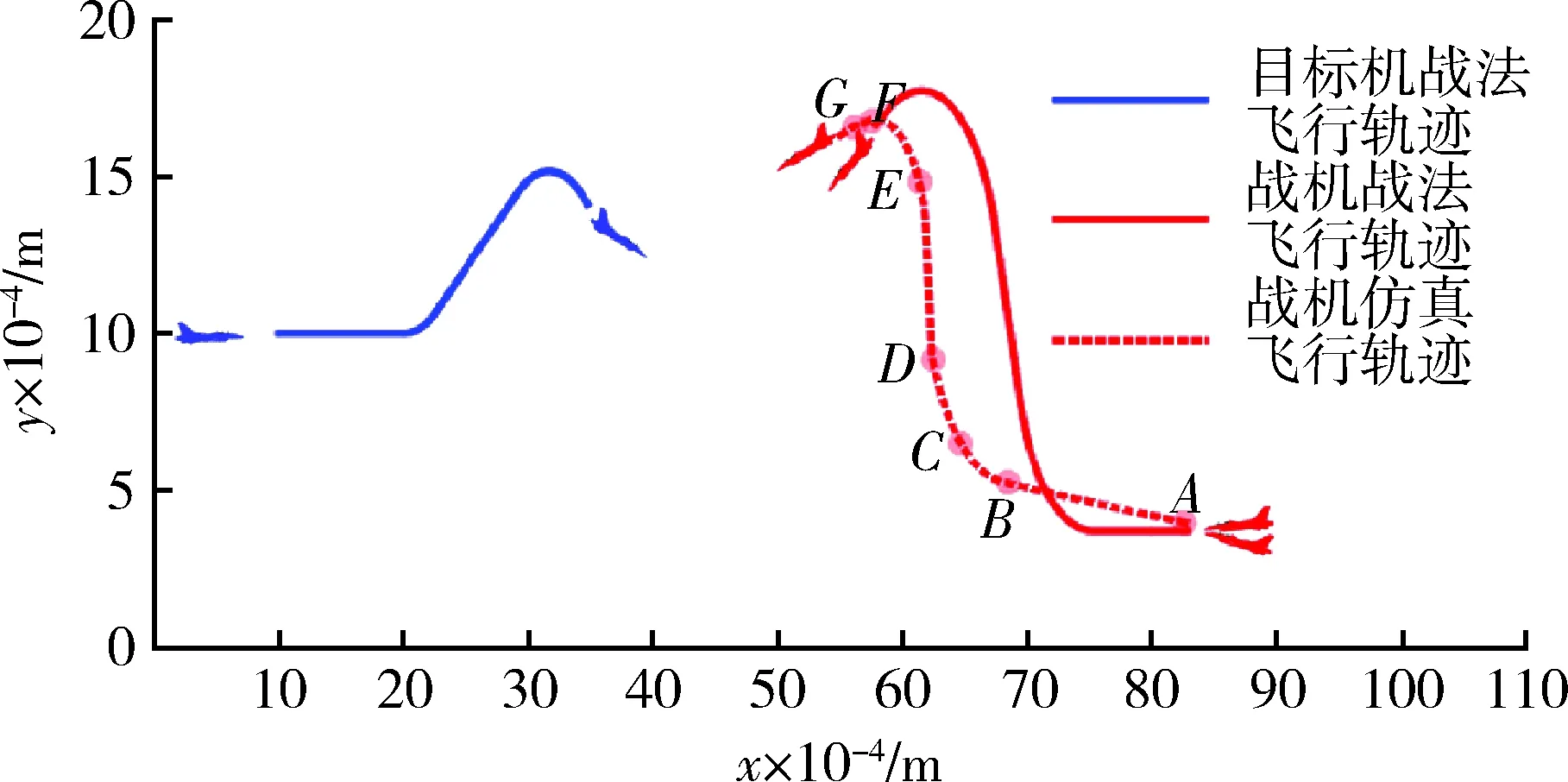
圖6 戰機與目標機飛行軌跡Fig.6 Flight paths of our fighter and target plane

將戰機仿真飛行軌跡與戰法飛行軌跡比較后可以初步得出，通過模型計算仿真得出的戰機航向、速度以及中距轉彎機動時機更加精確，能夠使戰機的機動更加有效，空戰優勢更加明顯，對目標機構成威脅。

在中距轉彎機動矢量模型中，戰機中距轉彎機動對策是實時生成的，表2列舉了6個特殊節點處的戰機機動對策指令。

當戰機與目標機都按照預先設定的戰法實施飛行時，在上述6個特殊時間節點處，戰機與目標機的綜合優勢值如表3所示。

當戰機按照本文建立的中距轉彎機動模型計算的結果實施機動時，在上述6個特殊時間節點處，戰機與目標機的綜合優勢值如表4所示。

從上述結果可以看出，初始時刻，戰機與目標機優勢相當，當戰機經過中距轉彎機動后，逐漸增加與目標機間的優勢差，對目標機構成威脅。比較表3與表4可以得出，通過模型計算得出的我方戰機機動對策更加具有可靠性，戰機的空戰優勢更加明顯，證明了模型的有效性。

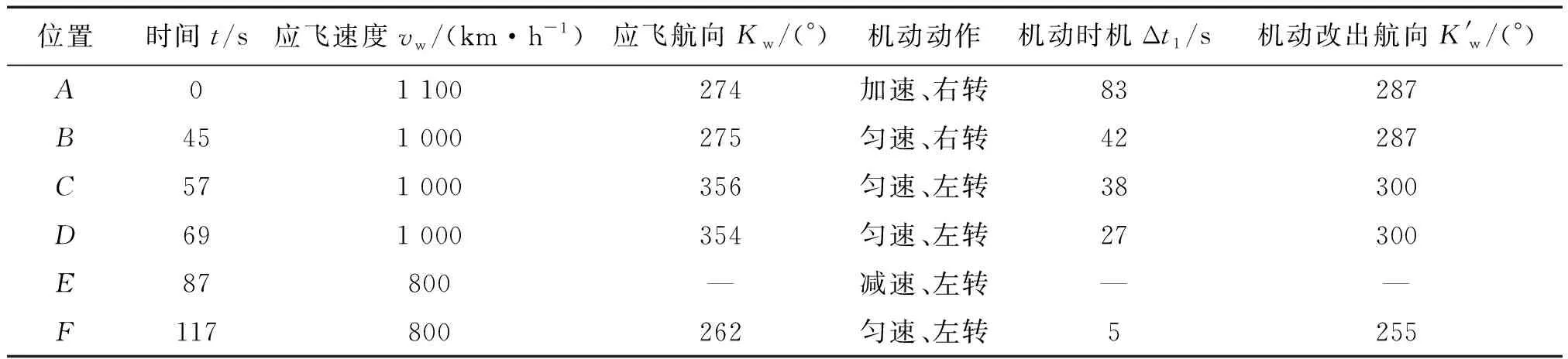
表2 特殊節點處戰機機動對策指令Table 2 Instructions for maneuver countermeasures of our fighter at special nodes

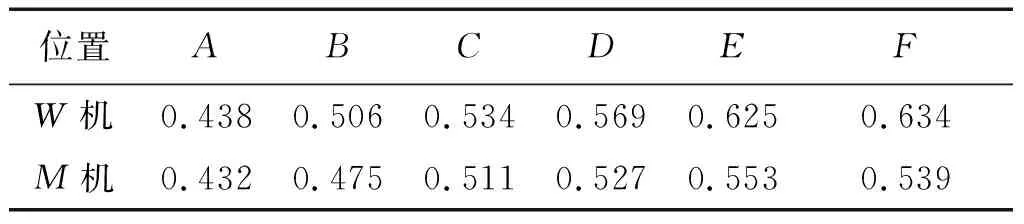
表3 戰法飛行兩機綜合優勢值Table 3 Comprehensive advantage value of our and target fighters flying with combat tactics

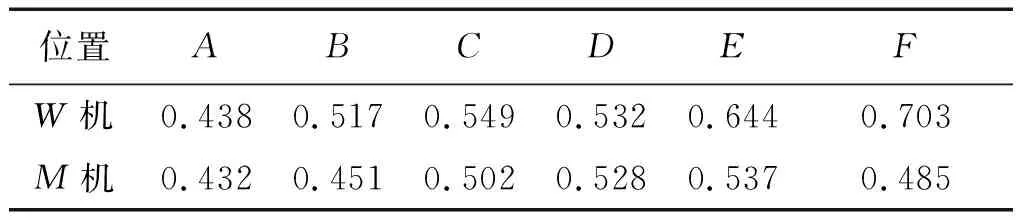
表4 模型仿真飛行兩機綜合優勢值Table 4 Comprehensive advantage value of our and target fighters flying with model simulation

4 結束語

自由空戰中，中距轉彎機動對策生成仍然具有十分重要的地位作用。本文將導彈最大攻擊區與戰機優勢函數相結合，通過對影響中距轉彎機動的因素進行分析，建立了中距轉彎機動矢量模型，并通過仿真分析，驗證了模型的有效性，對提升自由空戰中距轉彎機動對策生成的準確性具有重要意義。