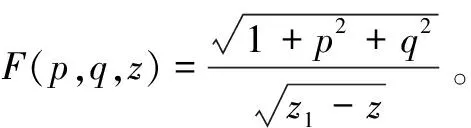最速降線問題的充分性
邢家省, 楊義川, 王擁軍
(1.北京航空航天大學數學與系統科學學院, 北京 100191;2.數學、信息與行為教育部重點實驗室, 北京 100191)
引 言
最速降線問題[1-6]是科學發現史上著名的問題,引起了人們持續不斷的研究興趣,開創了多個研究課題。該問題轉化為求一個泛函的最小值問題,這個泛函在最小值處的必要條件已經得到,泛函的臨界點的存在性已經解決了。泛函的臨界點是否為最小值點是需要證明的[1-6],文獻[2-4]在引入極值場和Hilbert不變積分的方法,對一般泛函的臨界點是泛函最小值的充分條件進行了研究,給出了最速降線問題的充分性證明,但這種證明方法不直接不自然。本文在綜合利用文獻[7-20]中思想方法的基礎上,對泛函的臨界點是泛函的最小值給出了直接簡單的證明方法,對泛函的臨界點的唯一性給出了證明,對最速降線必是在豎直平面內也給出了證明。
1 質點沿光滑軌道下滑所需的時間公式
著名的最速降線問題[1-6]表述如下:在一鉛直平面上,給定不在同一鉛直直線上兩點A,B。在重力作用下,一質點沿著過A,B兩點的光滑軌道L下滑。下滑的軌道L不同,質點由A點下滑到B點所需的滑動時間T也就不同。問當L是什么曲線時,所需的滑動時間T最短。
建立xOy坐標標系,Ox軸正向水平向右,Oy軸正向豎直向上。
設A點坐標為(x1,y1),B點坐標為(x2,y2),x1 設曲線L經過A點和B點,曲線L的方程為y=y(x),或者曲線L的方程為x=x(y) 。 設有一質點沿某曲線L由點A無摩擦地滑動到點B,考察所需的滑動時間T。 假設在時刻t質點已滑動了路程s,到達的位置為(x(t),y(t)), 由動能勢能守恒原理,可得 (1) 當曲線L的方程為y=y(x)時, 得 質點沿曲線L由點A無摩擦地滑動到點B,所需的時間[1-4]是 (2) 當曲線L的方程為x=x(y)時, 得 質點沿曲線L由點A無摩擦地滑動到點B,所需的時間[1-4]是 (3) 設曲線L的最低點在Ox軸上,質點在曲線L上高度為h的點處靜止開始下滑到最低點處所需時間[1-4]為 (4) 式(4)導致出現積分方程的問題[4]和等時曲線的求解問題[20]。 考慮泛函 (5) 設函數集合 M={x(y)∈C1[y2,y1],x(y2)=x2,x(y1)=x1} 顯然T(x)就是定義在M上的一個泛函。 于是,最速降線問題就是要在集合M上求出一個函數x=x(y), 使得泛函T(u)在處x=x(y)取得最小值, 在文獻[1-4]中,研究由(2)式表示的泛函的最小值問題,引入變分方法,尋找到泛函的臨界點。 記M0={x(y)∈C1[y2,y1],x(y2)=0,x(y1)=0},若泛函T(u)在x=x(y)處取得最小值,則對任意v∈M0,都有T(x+εv)在ε=0處達到最小值,于是 記 則 故有 (6) 進而得到 (7) 式(6)就是泛函T(u)在x處取得最小值的必要條件,也就是泛函的臨界點滿足的方程。顯然(6)式與(7)式是等價的。 下面證明泛函的臨界點的存在性。 對 有 代入式(7),得到 (8) 現對此常微分方程進行求解。 (8)式可化為如下的形式 (9) 對(9)式兩邊積分,則有 令 令u=csinθ, y=y1-c2sin2θ= 令t=2θ,則有 則得到泛函的臨界曲線的參數方程為 其中常數k,c1可由邊界條件來確定。 顯然最速降線為擺線的一部分[1-6]。泛函臨界點的存在性得證。這只是泛函取得最小值的必要條件。 以上給出了微分方程(8)的直接自然的求解過程,在文獻[1-4]中給出的是選取參數方程的代入方法,這種參數方程的選取方法不太自然。 對x+εv∈M,有 由于 由此可知,T(u)在M上的最小值在x∈M處達到。 這里,我們用直接的簡單方法,給出了充分性的證明。 關于泛函的臨界點是否為泛函的最小值點的問題,在文獻[2,3,4]中進行了一般性的研究,得到了一些充分性的結果。 設x1,x2∈M是問題(6)的兩個解, 于是 注意到 其中 從而有 特別取v=x2(y)-x1(y),則有 于是x2(y)-x1(y)=0,x2(y)=x1(y) 即得問題(6)的解是唯一的。 泛函的臨界點是唯一的,最速降線問題的解是唯一的。 在文獻[4,7,20]中,對積分方程(4)進行了求解,對等時曲線是擺線給出了求解證明。 建立空間直角坐標系Oxyz,水平面為xOy,Oz軸正向豎直向上。 設A點坐標為(x1,y1,z1),B點坐標為(x2,y2,z2),z2 設曲線L經過A點和B點,曲線L的方程為x=x(z),y=y(z),z=z。 設有一質點在重力作用下沿某曲線L由點A無摩擦地滑動到點B,考察所需的滑動時間T。 質點沿曲線L由點A無摩擦地滑動到點B,所需的時間[1-4]是 (10) 最速降線問題轉化為考慮泛函(10)式的最小值問題,由極值的必要條件,極值曲線滿足 其中C1,C2為常數。 C2x′(z)=C1y′(z) 對此積分,則得 C2x(z)=C1y(z)+C3 其中C3為常數。 這就得出,極值曲線必在豎直平面內,極值曲線是平面曲線。 由此證明了,最速降線必是平面曲線[10],最速降線一定在豎直平面內。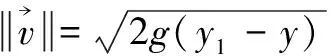
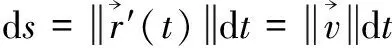
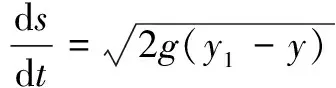
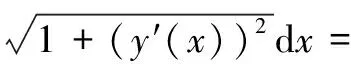
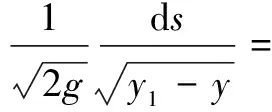
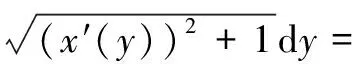
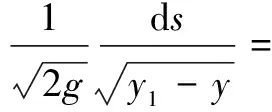
2 最速降線問題的泛函表示
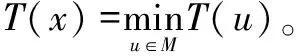
3 泛函在某函數處達到最小值的必要條件
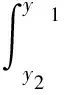
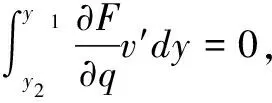
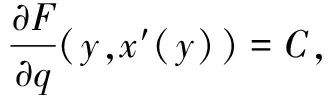
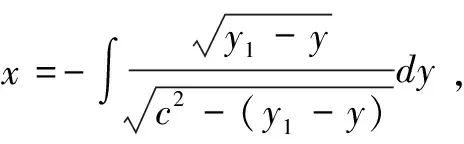
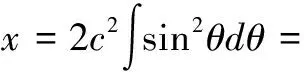
4 泛函的臨界點為最小值點的充分性的直接證明
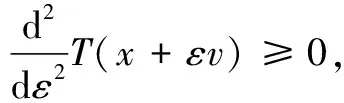
5 泛函的臨界點方程解的唯一性證明
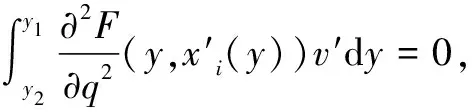
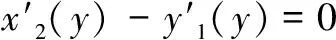
6 最速降線一定是在豎直平面內