動力學蒙特卡洛方法在計算物理教學中的引入

陳含爽

（安徽大學物理與材料科學學院，安徽合肥230601）

隨著計算機技術的快速發展，計算物理作為一門獨立的學科嶄露頭角，成為聯系理論物理和實驗物理的橋梁。計算物理也是大多數本科高等院校物理以及相近專業開設的一門本科生專業課。大多數計算物理教材都會涉及蒙特卡洛方法的介紹，如圓周率和定積分的計算、任意分布隨機數的產生等[1]。蒙特卡洛方法是發展最為成熟的計算機模擬方法之一，最早是在1957年由Metropolis和Ulam等針對中子輸運問題時提出的[2]。蒙特卡洛方法基本原理是基于多次隨機采樣來得到數值結果的計算機模型方法，已被廣泛地應用于數值優化和數值積分等問題。蒙特卡洛方法在許多領域均有廣泛的應用，如統計物理、計算生物學、金融學以及人工智能等領域[3]。

動力學蒙特卡洛方法是模擬一些實際過程時間演化的有效的蒙特卡羅方法，其應用范圍十分廣泛，包括晶體生長、表面反應和擴散等[4]。動力學蒙特卡洛方法的提出是為了解決常規蒙特卡洛方法效率不高的問題。例如，在模擬自旋模型的Metropolis算法中，自旋翻轉的嘗試可能不被執行，這些嘗試被稱為空事件，尤其在低溫情況下，空事件出現的可能性很大，這時蒙特卡洛模擬的效率就不高，動力學蒙特卡洛方法可以避免空事件的發生[5]。動力學蒙特卡洛方法和Gillespie算法[6]本質上是相同的，其算法實現是要回答兩個問題：一是下一個事件是什么時候發生，二是下一次發生的是哪一個事件。然而，大多數計算物理教科書都沒有涉及動力學蒙特卡洛方法的介紹。為此，本文嘗試通過簡潔的數學語言介紹動力學蒙特卡洛方法的基本原理以及實現方法。最后，通過一個簡單的例子——Susceptible-Infected-Susceptible：SIS傳播模型[7]，來闡述動力學蒙特卡洛方法實現的過程，以及如何進行結果分析和討論。

1 動力學蒙特卡洛方法的基本原理

現有n個獨立無關的隨機過程，假設過程本身發生的時間忽略不計，相繼兩次過程之間的等待時間τ滿足指數分布（泊松過程），即

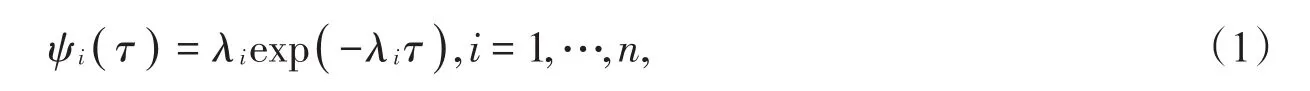
其中λi是第i個過程的發生速率。定義存活概率函數其含義是第i個過程的等待時間大于τ的概率，那么所有過程的存活概率為因此，整個過程的等待時間滿足概率密度函數是可以看出整個過程仍是泊松過程，任意一個過程發生的速率為所有過程發生速率之和，即因為存活概率是0到1之間的隨機數，所以等待時間可以寫做

其中r是0到1之間均勻分布的隨機數。第i個隨機過程發生的概率密度為

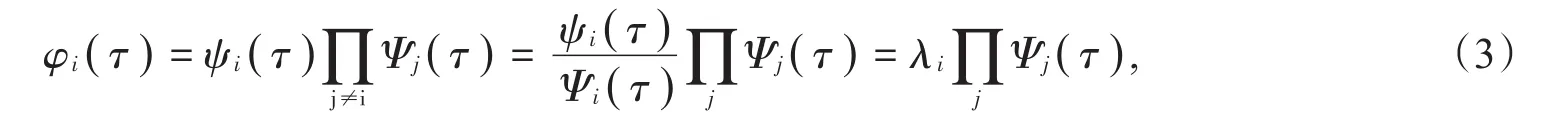
所以第i個隨機過程發生的概率為

基于上述理論，動力學蒙特卡洛方法可以總結為以下兩步：

（1）產生0到1之間的均勻分布的隨機數r，計算下一個過程發生的時間間隔更新時間

（2）產生另一個0到1之間的均勻分布的隨機數u，若滿足不等式則發生第j個隨機過程，更新粒子數和反應速率。

2 動力學蒙特卡洛方法的應用

作為一個具體例子，下面將動力學蒙特卡洛方法應用到SIS模型。給定一個大小為N的網絡，網絡上每個節點放置一個粒子，粒子的狀態要么是易感態（susceptible），用S表示，要么是感染態（infected），用I表示。一方面，一個S粒子與一個I粒子接觸，即這兩個粒子是鄰居節點，那么S粒子被感染變成I粒子的速率為λ；另一方面，一個I粒子自發地恢復成S粒子的速率為μ。這兩個過程可以表示成下列兩個反應：

SIS模型的動力學蒙特卡洛方法的實施如下：

（1）初始條件設置：隨機選擇一部分粒子作為感染種子節點（例如10%的節點），即這些種子節點的初始狀態設為I，剩下節點的初始狀態設為S。設定初始時間t=0，產生初始I粒子和SI邊的列表，記NI和NSI為I粒子和SI邊的數目。

（2）產生均勻分布的隨機數r∈[0,1]，計算下一個過程發生的時間間隔更新時間

（4）更新I粒子和SI邊的列表。回到（2）。

3 結果分析

定義有效感染系數β=λ μ。圖1給出了ER隨機網絡[8]上SIS模型的感染范圍ρ(t)=NI(t)N的3條時間序列，對應于3個不同的β值。當β較小時，最終的感染范圍變為零，稱之為健康態，該狀態是吸收態。吸收態的意思是一旦體系達到這個狀態，會永遠停留在此態[9]。對SIS模型來說，一旦所有節點的狀態都是S態，(5)式兩個反應都無法進行。當β較大時，最終的感染范圍會維持在某個值附近。由于有限大小網絡原因，感染范圍會在穩態值附近漲落，網絡規模越小，漲落越大。

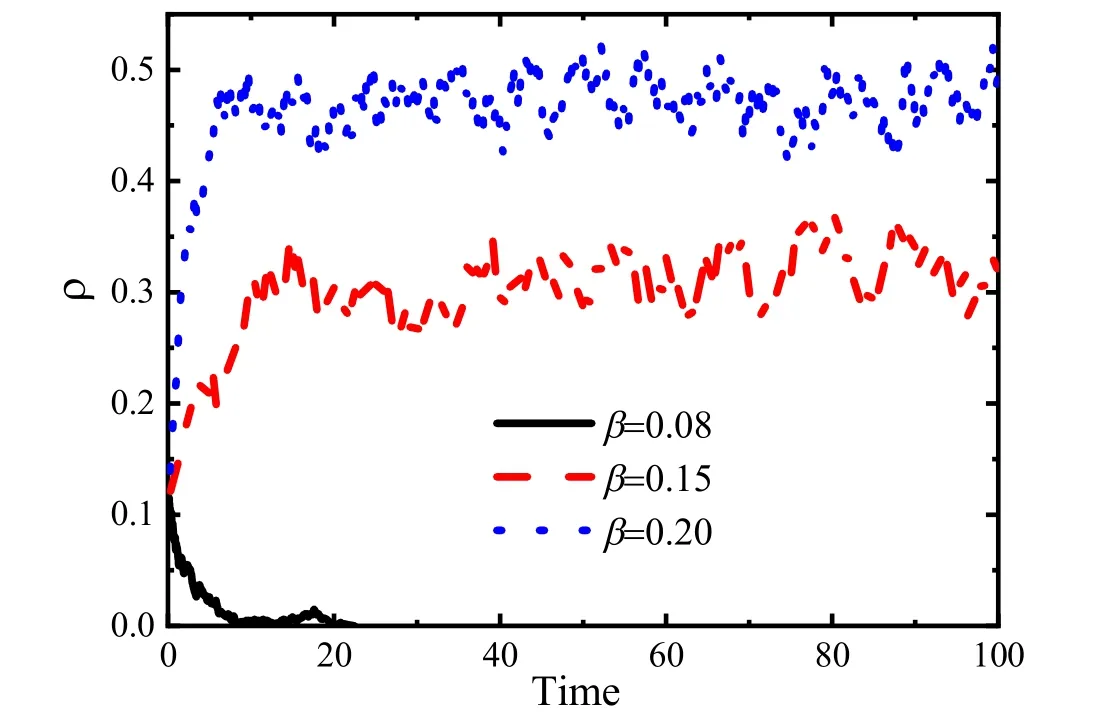
圖1 3個不同感染速率下的ER網絡上感染范圍ρ(t)的時間序列。網絡大小N=1 000，平均度 k=10

圖2 給出了β=0.15時兩次相繼反應之間的等待時間Δt的分布P( )Δt，如果將縱坐標設置成對數值，如圖2中的插圖所示，可以看出滿足指數分布，即這與之前泊松過程假設是一致的。

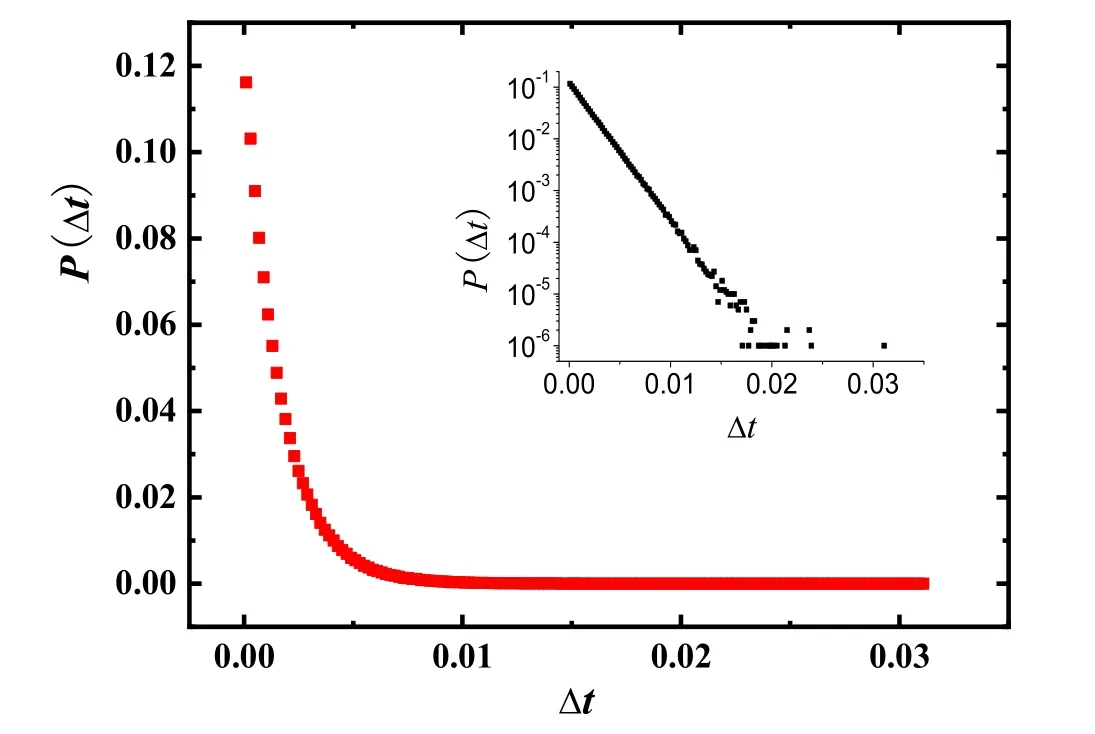
圖2 β=0.15時兩次相繼反應之間的等待時間Δt的分布P( )Δt

圖3 給出了感染范圍的穩態平均值 ρ隨有效感染系數β的變化圖，其中是采樣時間長度。當β＜βc時，ρ=0；當β＞βc時，ρ＞0。體系在傳播速率閾值β=βc時發生了相變。然而，當β稍稍大于βc時，感染范圍并不大，由于有限尺度漲落原因，體系很容易達到吸收態。因此，很難通過圖3來準確地定出傳播速率閾值，為此，采取準靜態方法來確定βc的值。準靜態方法的基本思想是：一旦體系達到吸收態，隨機地賦予體系的一個采用過的非吸收態構型。通過計算ρ的漲落有關的量，定義為極大值的位置給出傳播速率閾值βc的值，如圖4所示，βc=0.106。

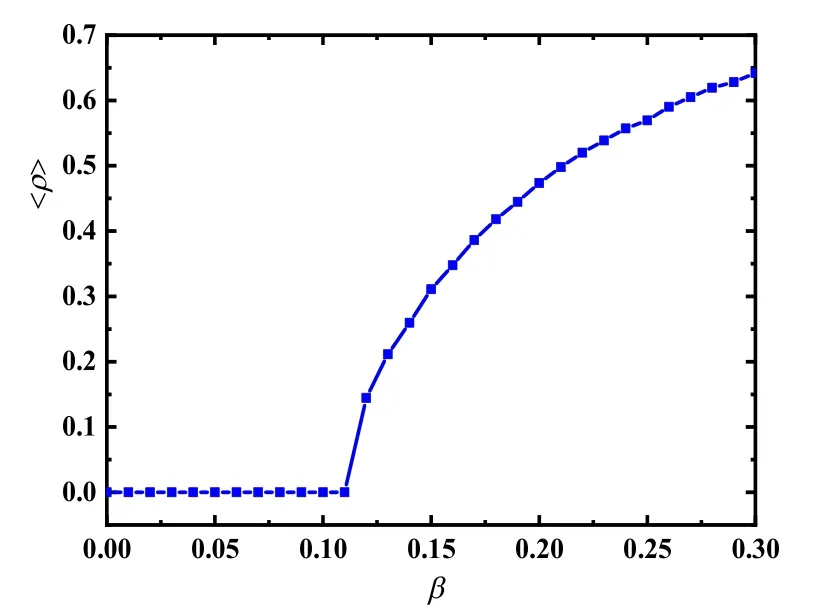
圖3 感染范圍的穩態平均值 ρ隨有效感染系數β的變化圖

圖4 χ隨有效感染系數β的變化圖

4 結論

本文介紹了動力學蒙特卡洛方法的基本原理以及程序實現的基本步驟，并以一個簡單的例子——網絡上SIS疾病傳播過程來說明動力學蒙特卡洛方法的實際應用。通過計算傳播范圍與傳播速率之間的關系來闡述該模型相變的性質，并通過計算漲落相關的物理量來確定相變的位置，即傳播速率的閾值。本文對動力學蒙特卡洛方法的基本原理的闡述是考慮了本科生對數學和物理知識掌握的實際程度，相信只要本科生掌握了一些微積分和概率論的知識，本文的推導是完全可以看懂的。此外，本文討論的是泊松過程，若隨機過程的等待時間不滿足指數分布，即非泊松過程，也可以使用類似的方法推導[11]。