數(shù)學物理中一維泊松方程基本解的兩種求法

周文杰，潘 婷，章禮華，馬業(yè)萬

（安慶師范大學物理與電氣工程學院,安徽安慶246133）

泊松方程是一個在理論物理和機械工程等領域應用廣泛的二階橢圓型偏微分方程，含該方程的定解問題通常均可采用格林函數(shù)法進行求解。在物理上，求解泊松方程的邊值問題本質上可以歸結為求相對應的格林函數(shù)，然后通過將求得的格林函數(shù)代入相應的泊松方程解的積分公式，就可以得到該定解問題的解。利用格林函數(shù)法求解時，需要用到與之相對應的基本解。數(shù)學物理上通常將不同維度下無界空間的格林函數(shù)稱為該維度上泊松方程的基本解。在國內外眾多數(shù)學物理方法教材和參考文獻中，如姚端正教授和德國顧樵教授在他們各自編寫的數(shù)學物理方法教材中均著重討論了三維和二維無界空間格林函數(shù)，并給出了十分詳細的求解方法及解的結果[1-2]，張宏浩教授針對三維無界空間格林函數(shù)也給出了詳細的傅里葉積分法求解過程[3]，但針對一維無界空間格林函數(shù)都鮮有討論，顯式的表達式也較為少見。為此，本文將在分析討論三維和二維泊松方程基本解的基礎上，分別采用類推法和積分解法，給出一維無界空間格林函數(shù)的表達式。

1 類推法求一維泊松方程的基本解

1.1 三維泊松方程的基本解

三維泊松方程的基本解，即三維無界空間格林函數(shù)G( )M,M0是下述含有三維δ函數(shù)的非齊次方程

為了求解三維無界空間上泊松方程（1），考慮到空間對稱性，通過選取球坐標系（選擇源點M0為坐標原點），利用傅里葉變換法[2]，可求得上述無界空間泊松方程（1）的基本解為

其中r為場點M到源點M0的距離，即r= ||MM0。

1.2 二維泊松方程的基本解

二維泊松方程的基本解，即二維無界平面所對應的格林函數(shù)滿足下述含有二維δ函數(shù)的非齊次方程

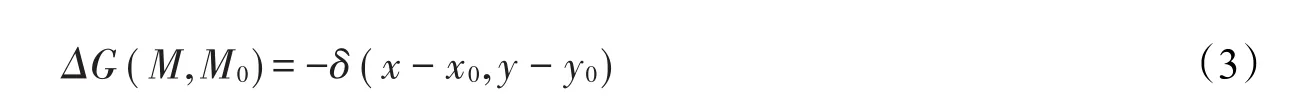
的解，其中二維δ函數(shù)可以表示為δ(M-M0)= δ(x-x0,y-y0)，M=M(x,y)，M0=M(x0,y0)，-∞ ＜ x,y ＜ +∞。

選取源點M0為坐標原點，在極坐標系下對（3）式求解[1]，可得二維無界平面上的格林函數(shù)為

其中r為二維平面上場點M到源點M0的距離，也即二維泊松方程的基本解為，它與垂直于XOY平面的具有單位線密度的無限長線電荷在r處所形成的電勢函數(shù)相對應，其中ε為介電常數(shù)，這也正是二維泊松方程基本解的電勢物理意義。

1.3 類推法求一維泊松方程的基本解

基于上述結果，下面從格林函數(shù)為勢函數(shù)的物理意義出發(fā)，通過類推給出一維泊松方程的基本解。無界空間格林函數(shù)在三維情形下表示放置于坐標原點的單位點電荷在三維空間任意r= ||MM0=處所形成的電勢，在二維情形下表示線密度ρ=1的垂直于XOY平面的無限長線電荷在處所形成的電勢。單位點電荷可以看作是線密度ρ=1的無限長線電荷在原點處的投影，而線密度ρ=1的無限長線電荷可以視為面密度σ=1的無限大面電荷的投影。結合電磁學的知識[4]，面密度σ=1的垂直于x軸的無限大面電荷在一維空間任意r處產生的電勢函數(shù)為φ=-r/2ε，其中ε為介電常數(shù)再結合三維和二維泊松方程基本解的表達形式和物理意義，可以類推給出一維泊松方程

的基本解，即一維無界空間格林函數(shù)，可以用面密度σ=1的垂直于x軸的無限大面電荷在一維空間任意r處形成的電勢函數(shù)來表示，也即（5）式的基本解可以表示為

其中r表示x軸上點到平面的距離。將上述分析討論的結果總結如表1所示。

表1 三維、二維和一維情形下電勢函數(shù)和格林函數(shù)

2 積分法求一維泊松方程的基本解

一維泊松方程的基本解即一維格林函數(shù)滿足的泊松方程為

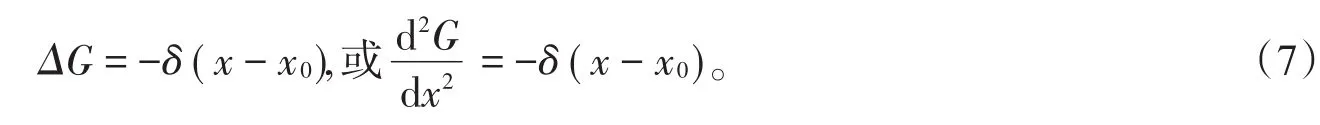
由δ函數(shù)的性質[5-6]可得

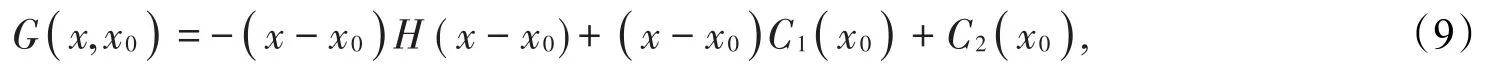
其中x0在物理上表示源點，考慮到G在物理上表示勢函數(shù)，取x0處為零電勢參考點，則C2( )x0=0。又由對稱性可得根據(jù)階躍函數(shù)的性質，有解得C1( )x0=則可得到格林函數(shù)為即

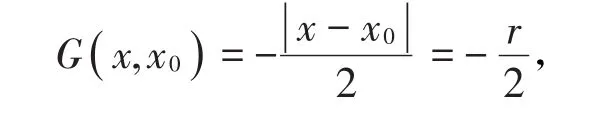
其中，r為x軸上的點到過源點x0且垂直于x軸的平面的距離。

3 結束語

綜上所述，本文分析了三維和二維泊松方程基本解的電勢物理意義，并運用類推的方法得出了一維泊松方程基本解，即一維無界空間格林函數(shù)的顯式數(shù)學表達式。在此基礎上，通過直接積分法求解一維泊松方程基本解，與類推法得出的結果完全一致。該方法對于泊松方程基本解的學習和應用于定解問題的求解具有重要的參考價值，也有利于加深學生對格林函數(shù)的整體理解。